LoRA: Low-Rank Adaptation of Large Language Models
该论文来自微软团队,LoRA微调现已成为大模型常用的高效微调方法之一。
背景
预训练-微调范式是当前使用最广的范式,能够提升模型在下游任务上的表现。但是当模型参数规模变大,全量微调需要消耗大量资源和时间,就变得不太可行。因此出现了许多高效微调(peft, p arameter e fficient f ine-tuning)的方法,例如谷歌团队提出的Adapter Tuning、斯坦福团队提出的Prefix-Tuning、清华团队提出的P-Tuning v2等。但他们各自都有一些缺点:
- Adpter Tuning增加了模型的层数,导致推理延迟提高。
- Prefix Tuning难于训练,并且引入了前缀prompt,占用了下游任务的输入序列空间,影响模型表现。
- P Tuning v2容易产生灾难性遗忘,微调后的模型在之前的任务上表现会变差。
动机
深度神经网络包含大量稠密层,这些层的参数矩阵一般都是满秩的。现有的工作表明,训练后的模型是过度参数化的,他们实际上存在一个较低的intrinsic dimension(内在维度),即高维数据实际上是在低维的子空间中。因此作者假设在模型适配下游任务的过程中,参数改变量上也存在一个"内在秩",可以对增量参数据进行低秩分解。
问题定义
以自回归的语言模型为例,给定一个参数为 Φ \Phi Φ的预训练语言模型 P Φ ( y ∣ x ) P_{\Phi}(y|x) PΦ(y∣x),全量微调的目标是让模型初始化为 Φ 0 \Phi_0 Φ0,然后通过最大化条件概率被更新为 Φ 0 + Δ Φ \Phi_0+\Delta \Phi Φ0+ΔΦ。
m a x Φ ∑ ( x , y ) ∈ Z ∑ t = 1 ∣ y ∣ log ( P Φ ( y t ∣ x , y < t ) ) \underset{\Phi}{max}\underset{(x,y)\in \mathcal{Z}}{\sum}\overset{|y|}{\underset{t=1}{\sum}}\log(P_{\Phi}(y_t|x,y_{<t})) Φmax(x,y)∈Z∑t=1∑∣y∣log(PΦ(yt∣x,y<t))
但进行这种方式微调,学习到的增量参数 Δ Φ \Delta \Phi ΔΦ的维度和与训练参数 Φ 0 \Phi_0 Φ0的维度是一样的,所需的资源也就非常多。如果采取高效微调的方式,那么可以找到少量的参数 Θ \Theta Θ,使得 Δ Φ = Δ Φ ( Θ ) \Delta \Phi = \Delta \Phi(\Theta) ΔΦ=ΔΦ(Θ),其中 ∣ Θ ∣ < < ∣ Φ 0 ∣ |\Theta| <<|\Phi_0| ∣Θ∣<<∣Φ0∣,那么下游优化目标就变成如下:
m a x Θ ∑ ( x , y ) ∈ Z ∑ t = 1 ∣ y ∣ log ( P Φ 0 + Δ Φ ( Θ ) ( y t ∣ x , y < t ) ) \underset{\Theta}{max}\underset{(x,y)\in \mathcal{Z}}{\sum}\overset{|y|}{\underset{t=1}{\sum}}\log(P_{{\Phi_0}+\Delta \Phi(\Theta)}(y_t|x,y_{<t})) Θmax(x,y)∈Z∑t=1∑∣y∣log(PΦ0+ΔΦ(Θ)(yt∣x,y<t))
这就意味着用参数量更少的 Θ \Theta Θ来低秩降维近似原先的参数增量。相比于其他方法,这种方法不会增加推理耗时,同时更便于优化。
实现原理
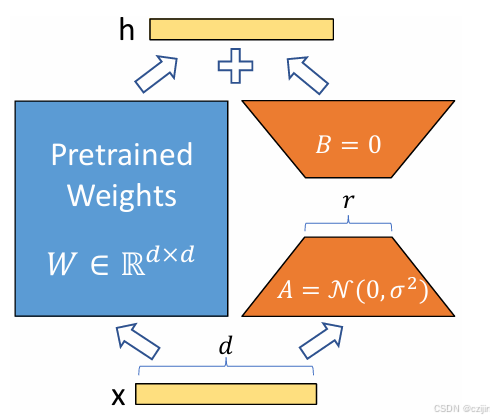
LoRA的核心思想就一句话:冻结原有模型参数,用参数量更小的矩阵进行低秩近似训练。
对于预训练权重矩阵 W 0 ∈ R d × k W_0 \in \mathbb{R}^{d \times k} W0∈Rd×k和增量参数矩阵 Δ W \Delta W ΔW,可以有以下等式:
W 0 + Δ W = W 0 + B A W_0 + \Delta W = W_0 + BA W0+ΔW=W0+BA
其中 B ∈ R d × r B \in \mathbb{R}^ {d \times r} B∈Rd×r和 A ∈ R r × k A \in \mathbb{R}^{r \times k} A∈Rr×k为LoRA的低秩适应权重矩阵, r < < m i n ( d , k ) r << min(d,k) r<<min(d,k)。那么此时,微调的参数量就从 d × k d \times k d×k变成了 d × r + r × k d \times r + r \times k d×r+r×k,这个参数量远小于全量微调的参数量。
考虑前向传播,那么此时就有
h = W 0 x + Δ W x = W 0 x + B A x h = W_0x + \Delta Wx = W_0x+BAx h=W0x+ΔWx=W0x+BAx
训练时由于 W 0 W_0 W0被冻结,因此不会计算其对应梯度,更不会更新其参数,推理时只需要将 B A BA BA合并到 W 0 W_0 W0中即可,不存在推理延迟。
细节分析
进行微调时,我们需要更新A和B的参数,那么一开始该如何初始化呢?一般来说需要保证一开始的参数量和模型的原参数量相同,即 Δ W = 0 \Delta W = 0 ΔW=0。那么就可能有这种初始化方式:A=0,B!=0;A!=0,B=0;A=0,B=0
首先,当A=0,B=0时,B和A就无法继续做梯度更新,权重梯度全部为0,处于鞍点。因此至少要保证A和B有一个为0一个不为0.
B的梯度 ∂ L ∂ B \frac{\partial L}{\partial B} ∂B∂L依赖A,A的梯度 ∂ L ∂ A \frac{\partial L}{\partial A} ∂A∂L也依赖B,如果仅有一项为0,那么是可以获取梯度进行训练的。
令 z = BAx, ∂ L ∂ A = ∂ L ∂ h ∂ h ∂ z ∂ z ∂ A \frac{\partial L}{\partial A} = \frac{\partial L}{\partial h} \frac{\partial h}{\partial z} \frac{\partial z}{\partial A} ∂A∂L=∂h∂L∂z∂h∂A∂z, ∂ L ∂ B = ∂ L ∂ h ∂ h ∂ z ∂ z ∂ B \frac{\partial L}{\partial B} = \frac{\partial L}{\partial h} \frac{\partial h}{\partial z} \frac{\partial z}{\partial B} ∂B∂L=∂h∂L∂z∂h∂B∂z 其中: ∂ z ∂ A = B x T , ∂ z ∂ B = A x T \frac{\partial z}{\partial A} = Bx^T, \frac{\partial z}{\partial B} = Ax^T ∂A∂z=BxT,∂B∂z=AxT
因此, ∂ L ∂ A = ( ∂ L ∂ h ) ⋅ ( ∂ h ∂ z ) ⋅ ( B x T ) \frac{\partial L}{\partial A} = (\frac{\partial L}{\partial h}) \cdot (\frac{\partial h}{\partial z}) \cdot (Bx^T) ∂A∂L=(∂h∂L)⋅(∂z∂h)⋅(BxT) , ∂ L ∂ B = ( ∂ L ∂ h ) ⋅ ( ∂ h ∂ z ) ⋅ ( A x T ) \frac{\partial L}{\partial B} = (\frac{\partial L}{\partial h}) \cdot (\frac{\partial h}{\partial z}) \cdot (Ax^T) ∂B∂L=(∂h∂L)⋅(∂z∂h)⋅(AxT) ,令 g = ( ∂ L ∂ h ) ⋅ ( ∂ h ∂ z ) g= (\frac{\partial L}{\partial h}) \cdot (\frac{\partial h}{\partial z}) g=(∂h∂L)⋅(∂z∂h) 则, ∂ L ∂ A = g ⋅ ( B x ) T \frac{\partial L}{\partial A} = g \cdot (Bx)^T ∂A∂L=g⋅(Bx)T, ∂ L ∂ B = ( A T g ) ⋅ x T \frac{\partial L}{\partial B} = (A^Tg) \cdot x^T ∂B∂L=(ATg)⋅xT
当A=0,B=0为0时,可以发现A和B的梯度全部为0,导致模型卡住无法学习。
当A=0,B不为0时,A的梯度不为0,B的梯度为0,A可更新,B不可更新。
当A不为0,B=0时,A的梯度为0,B的梯度不为0,A不可更新,B可更新。
论文中的推荐初始化方式为B初始化为0,A初始化为高斯分布,这是因为第一步只更新B,B开始逐渐学习增量,A保持不变。随着B的增大,B不为0时,A的梯度也不为0了,A也开始参与优化,因此最终AB就接近最优的低秩增量。
实际上两种方式是对称的,都可以对权重进行更新,参考[]((29 封私信 / 65 条消息) LoRA中初始化 A!=0、B=0,反过却不行吗? - 知乎)
在实际实现的时候, Δ W = B A \Delta W = BA ΔW=BA会乘以系数 α r \frac{\alpha}{r} rα与预训练权重合并 W 0 W_0 W0, α \alpha α是一个超参数。给定一个或多个下游任务数据,进行LoRA微调:
- 系数越大,LoRA微调权重的影响就越大,在下游任务上越容易过拟合
- 系数越小,LoRA微调权重的影响就越小(微调的效果不明显,原始模型参数受到的影响也较少)