给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。

分析:
这个问题的本质是一个组合枚举问题。给定一个不含重复元素的数组 candidates 和一个目标值 target,我们需要从数组中选取若干个数字,使它们的和正好等于 target,并且要列出所有可能的组合。由于每个数字都可以被无限次重复选取,因此问题的关键不在于选不选,而在于如何系统地遍历所有可能的选择路径。
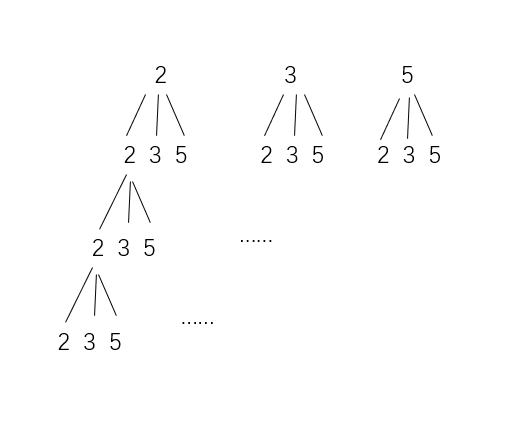
对于这种需要枚举所有组合的问题,回溯法是非常合适的,可以参考之前做过的电话号码的字母组合问题。回溯可以理解为:沿着一条选择路径不断向下尝试,每次选择一个数字加入当前组合中。如果当前数字之和还没有达到 target,就继续向下递归;如果发现当前和已经超过了 target,说明这条路径不可能再得到合法结果,此时就应该立刻停止继续尝试,回退到上一个选择点,换一条路继续探索;当数字之和刚好等于 target 时,说明找到了一种可行组合,可以将当前路径记录下来。
整个搜索过程可以类比为走迷宫。candidates 中的每一个数字都相当于一条岔路,path 表示当前正在行走的路线。只要这条路线上的数字之和不超过 target,就可以继续往前走;一旦超过 target,就意味着走进了死胡同,需要马上原路返回,这一步就是一种剪枝,可以避免继续在无意义的路径上浪费时间。当恰好走到和为 target 的位置时,就相当于找到了一个出口,可以记录这条完整路径。比如candidates = [2,3,6,7], target = 7的时候,第一次先选一个数2,把2加入到path中,这时还没有达到target的值,可以再选一个数,这时还是可以按顺序选[2,3,6,7]中的所有数,做循环尝试,可以就再选2试试,这时path中已经有[2,2]了,和还是没达到target,还可以继续加数,再加一个2试试,最后发现[2,2,2]后面再加数已经不行了,加任何数都走不通了,那么就会把最后加进去的那个 2 踢掉,回到 [2, 2] ,然后在这一层尝试别的选择。
为了保证有更高的效率,可以先对 candidates 进行排序。这样一来,当遍历到某个数字时,如果发现它已经大于当前剩余的 target,就可以直接停止本层循环,因为这个增序序列后面的数字只会更大,所以也就不必再继续尝试后面的数字了。这样做可以减少搜索空间,是回溯中非常重要的一种剪枝优化。
在组合的过程中,可能会出现顺序不同但本质相同的重复组合(例如 [2,2,3] 和 [2,3,2]),所以在递归过程中通过一个 start 下标来限制下一次选择的起始位置,保证每条路径中的数字都是按照固定顺序选取的。也就是说,[2,3,6,7]中,如果先选了2,那么下一步可以选2,3,6,7,但是如果先选3的话,后面就只能选6,7,不会再去选2了,因为之前的情况已经包含这个序列了。所以[2,3] 会出现,[3,2] 永远不会出现,每一种"数字集合"只会生成一次。同时,由于题目允许同一个数字被重复使用,比如第一次选了2第二次还是可以选2,所以递归时仍然从当前下标 start 开始选择2,而不是从下一个位置开始。
在整个搜索过程中,始终关注这三样东西:
-
当前组合 path,表示目前已经选了哪些数字,是一条"正在走的路径"
-
剩余的 target:表示还差多少才能凑够目标,每选一个数字,就让 target 减小
-
起始位置 start,为了控制下一步从哪个数字开始选,为了防止出现重复组合
用下面的例子来走一遍
candidates = [2, 3, 5]
target = 8
一、初始状态(根节点)
path = []
剩余 target = 8
可选数字:2, 3, 5
二、从 2 开始尝试
1. 选择 2
path = [2]
剩余 target = 8 - 2 = 6
2 . 再选 2
path = [2, 2]
剩余 target = 6 - 2 = 4
**3.**再选 2
path = [2, 2, 2]
剩余 target = 4 - 2 = 2
4. 再选 2
path = [2, 2, 2, 2]
剩余 target = 2 - 2 = 0
target == 0,命中目标,记录结果[2,2,2,2]
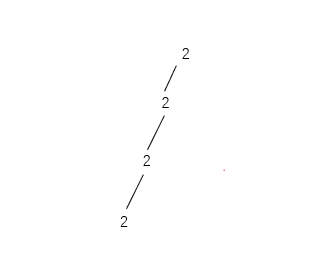
回溯(返回上一层)
撤销最后一次选择:
path = [2, 2, 2]
剩余 target = 2
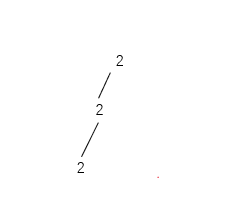
5. 尝试下一个数字 3
3 > 剩余 target 2,不可能成功,剪枝
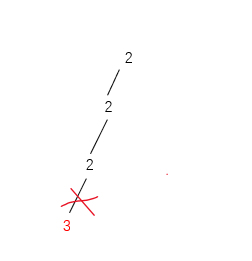
这一层结束,回溯到上一层
path = [2, 2]
剩余 target = 4
6. 尝试 3
path = [2, 2, 3]
剩余 target = 4 - 3 = 1
继续往下尝试,试到2的时候就发现候选数 >剩余target1,说明所有候选数都不行
走不通,把第三层的3踢出,回溯
path = [2, 2]
剩余 target = 4
7. 尝试 5
5 > 剩余 target4,所以剪枝
这是第二个2的所有情况都试过了, 本层结束,把第二层的2踢出,回溯
回到第一层 path = [2]
剩余 target = 6
8. 尝试 3
path = [2, 3]
剩余 target = 6 - 3 = 3
9. 再选 3
path = [2, 3, 3]
剩余 target = 3 - 3 = 0
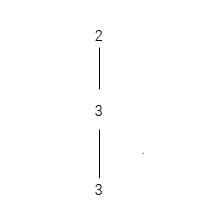
target == 0,命中目标,记录结果[2,3,3]
回溯到上一层
path = [2, 3]
剩余 target = 3
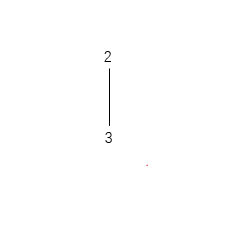
10. 尝试 5
5 > 3,剪枝, 回溯
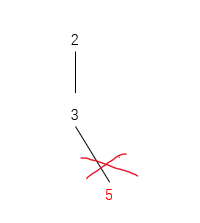
此时第二层的3已经所有情况都试过了,所以回到path = [2],剩余 target = 6
11. 尝试 5
path = [2, 5]
剩余 target = 6 - 5 = 1
走不通
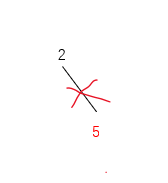
这时第一层是2的所有情况已经试完了,回溯
path = []
剩余 target = 8
三、第一层从 3 开始尝试,这时往后面走的话已经不会再去选2了,而是在3,5里面选。
1. 选择 3
path = [3]
剩余 target = 8 - 3 = 5
2. 再选 3
path = [3, 3]
剩余 target = 5 - 3 = 2
3 > 2,剪枝
回溯到path = [3]
剩余 target = 5
3. 选择 5
path = [3, 5]
剩余 target = 5 - 5 = 0
命中目标,记录[3,5]
此时第一层是3的情况也全部试完了,回溯到path = []
剩余 target = 8
四、第一层是5的情况,这时第二三层只能从 5 开始尝试,不能再选2,3了
1. 选择 5
path = [5]
剩余 target = 8 - 5 = 3
5 > 3
所以走不通
五、搜索结束
**最终结果 res
2,2,2,2
2,3,3
3,5\]**
C++代码实现:
```cpp
class Solution {
public:
vector