【DL】从零构建智能：神经网络前向传播、反向传播与激活函数深度解密

🏠 个人主页: EXtreme35

📚 个人专栏: DL

- 一、引言
- - [1.1 破除误区：你以为的"像大脑"，和我说的"像大脑"](#1.1 破除误区：你以为的“像大脑”，和我说的“像大脑”)
  - [1.2 核心疑问：为什么神经网络需要那么多层？](#1.2 核心疑问：为什么神经网络需要那么多层？)
  - [1.3 两层网络的魔力：空间扭曲与特征组合](#1.3 两层网络的魔力：空间扭曲与特征组合)
- 二、前向传播
- - [2.1 从单个神经元开始：智能的最小单元](#2.1 从单个神经元开始：智能的最小单元)
  - [2.2 扩展到全连接层：矩阵运算的优雅](#2.2 扩展到全连接层：矩阵运算的优雅)
  - [2.3 多层网络的链式传递：深度学习的"深"](#2.3 多层网络的链式传递：深度学习的“深”)
  - [2.4 NumPy 实现一个 3 层网络的前向传播](#2.4 NumPy 实现一个 3 层网络的前向传播)
- 三、激活函数专题
- - [3.1 为什么需要激活函数？](#3.1 为什么需要激活函数？)
  - [3.2 激活函数家族图谱：演进与选择](#3.2 激活函数家族图谱：演进与选择)
  - - [3.2.1 Sigmoid：保守型（将一切压到 0-1）](#3.2.1 Sigmoid：保守型（将一切压到 0-1）)
    - [3.2.2 Tanh ：平衡型（-1 到 1，均值 0）](#3.2.2 Tanh ：平衡型（-1 到 1，均值 0）)
    - [3.2.3 ReLU (Rectified Linear Unit)：激进型（要么活跃要么死亡）](#3.2.3 ReLU (Rectified Linear Unit)：激进型（要么活跃要么死亡）)
    - [3.2.4 Leaky ReLU / ELU / Swish：现代解决方案](#3.2.4 Leaky ReLU / ELU / Swish：现代解决方案)
  - [3.3 激活函数选择决策树](#3.3 激活函数选择决策树)
- 四、反向传播深度解析
- - [4.1 损失函数：量化"错误"的尺子](#4.1 损失函数：量化“错误”的尺子)
  - [4.2 链式法则：梯度倒流的"交通规则"](#4.2 链式法则：梯度倒流的“交通规则”)
  - [4.3 权重更新：走下山谷](#4.3 权重更新：走下山谷)
- 五、常见陷阱与最佳实践
- - [5.1 权重初始化：打破对称性](#5.1 权重初始化：打破对称性)
  - [5.2 梯度消失与爆炸](#5.2 梯度消失与爆炸)
  - [5.3 学习率的选择](#5.3 学习率的选择)
  - [5.4 始终先在小数据集上"过拟合"](#5.4 始终先在小数据集上“过拟合”)
  - [5.5 数值稳定性](#5.5 数值稳定性)

导语：你是否曾对人工智能背后的"黑科技"感到好奇？是否想知道计算机是如何"学习"和"思考"的？深度学习作为人工智能的核心，其最基本的运作原理------神经网络，其实并非遥不可及的魔法。这不仅是冷冰冰的代码，更是数学与工程的优雅交响曲。我们将用通俗易懂的可视化、生动比喻和逐步拆解的代码，彻底揭开神经网络的神秘面纱，带你从零开始，亲手构建一个属于你自己的智能模型！

一、引言

如果你曾对AI充满好奇，或者在学习深度学习时被那些复杂的公式和概念劝退，那么恭喜你，你来对地方了！

我们很多人第一次听到"神经网络"这个词，脑海中立刻会浮现出人类大脑中那些密密麻麻的神经元，它们复杂而神秘，支撑着我们的思考、感知和记忆。没错，神经网络的灵感确实来源于生物神经元。但在这里，我想先打破一个常见的误区：

1.1 破除误区：你以为的"像大脑"，和我说的"像大脑"

生物神经元：一个奇迹般的有机体

你的大脑里有数千亿个神经元，它们通过复杂的电化学信号（神经递质）进行异步通讯。每一个神经元都可以接收来自成千上万个其他神经元的输入，然后决定是否要"点火"，将信号传递给下一个神经元。这是一个极其精妙的生物处理器，能够进行模式识别、决策制定和情感体验------这一切的复杂性，是我们目前的人工智能还无法完全复制的。
人工神经元（M-P模型）：一个"加权求和+激活"的数学模型

与生物神经元相比，我们的人工神经元（由沃伦·麦卡洛克和沃尔特·皮茨在1943年提出，简称M-P模型）则要"简单粗暴"得多。它不是在"思考"，而是在进行高维空间的几何变换。你可以把它想象成一个小小的决策单元：
1. 它接收多个输入信号。
2. 给每个输入信号分配一个重要性权重。
3. 将所有加权后的信号累加起来，再加上一个偏置值（bias，可以看作是"基础兴奋度"）。
4. 最后，通过一个激活函数（一个非线性函数）来决定是否"兴奋"并输出信号。
【深度思考】：为什么说人工神经元"简单粗暴"？因为它无法真正模拟生物神经元复杂的时序依赖、突触可塑性、自适应学习规则等高级特性。但正是这种简化，让它变得可以在计算机上高效实现，并被大规模堆叠。

1.2 核心疑问：为什么神经网络需要那么多层？

你可能会问："既然一个神经元能做决策，我堆一大堆神经元在同一层不就行了吗？为什么非要搞成好几层，甚至几十层、上百层？"

这是一个非常好的问题！它触及了深度学习"深度"二字的精髓。我们来通过一个经典的例子，让你直观感受"层"的魔力：XOR（异或）问题。

【XOR问题简介】 XOR问题是人工智能领域的"hello world"级别挑战。它要求我们构建一个模型，当两个输入不同时，输出1（True）；当两个输入相同时，输出0（False）。

我们用数字表示：

输入 (0, 0) -> 输出 0
输入 (0, 1) -> 输出 1
输入 (1, 0) -> 输出 1
输入 (1, 1) -> 输出 0

现在，想象我们把这四个数据点画在一个二维坐标系上：

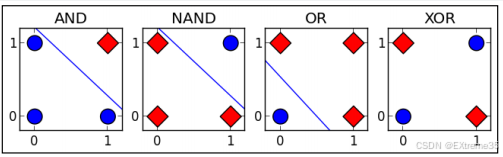
你尝试用一条直线（单层感知机只能做线性分割）将红色点和蓝色点完美分开，能做到吗？答案是不能。无论你如何画，总会有一些点被分错。

这就是单层感知机 的局限性！它只能处理线性可分的问题。而真实世界中的大多数问题，都是非线性的。

1.3 两层网络的魔力：空间扭曲与特征组合

当我们在单层感知机和输出层之间，加入一个隐藏层 时，奇迹发生了！

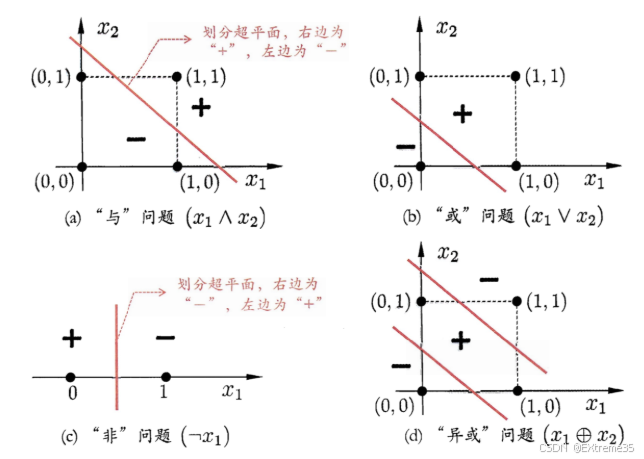
这个隐藏层，就像一个魔术师，它对原始输入空间进行了一系列非线性的"扭曲"和"变换" 。通过这些变换，原本纠缠在一起的数据点，在新的高维空间中变得线性可分了！输出层此时只需要画一条直线，就能完美区分它们。

这个例子告诉我们：

深度（多层）赋予了神经网络处理非线性问题的能力。
每一层都在学习抽取数据中不同层次的特征表示。第一层可能识别边缘、角点；第二层可能组合出简单的形状；更深层可能识别出物体的局部，最终在输出层识别出完整的物体。

所以，当我们在谈论"深度学习"时，这个"深度"指的就是多层神经网络。正是这些层层叠叠的非线性变换，赋予了神经网络惊人的学习能力和泛化能力。

在接下来的内容中，我们将以这个XOR问题为例，贯穿全文，并承诺你，读完这篇文章，你将能够自己推导神经网络中的所有核心公式，甚至用 NumPy 亲手实现一个简易的神经网络！准备好了吗？让我们开始这场烧脑但又充满乐趣的智能之旅！

二、前向传播

想象一下，你的神经网络就像一个精密的多级信号处理流水线 。数据从"原材料"入口进入，经过一道道工序（每一层神经元），最终在"产品"出口得到我们想要的预测结果。这个从输入到输出的过程，就是前向传播（Forward Propagation）。

2.1 从单个神经元开始：智能的最小单元

我们先聚焦到流水线上的一个最小工位------单个神经元。

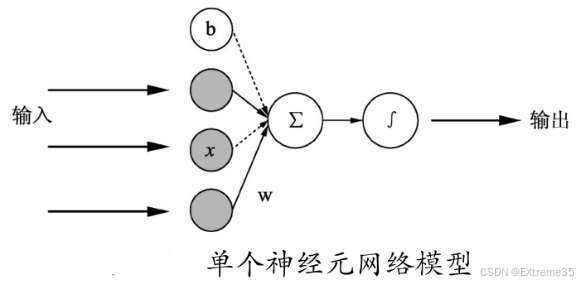
如图所示，一个神经元接收多个输入 x 1 , x 2 , ... , x n x_1, x_2, \ldots, x_n x1,x2,...,xn。

它对每个输入 x i x_i xi 乘以一个对应的权重 w i w_i wi，然后将这些乘积全部加起来，再加上一个偏置 b b b。这个求和结果我们称之为 z z z。

z = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b z = w_1 x_1 + w_2 x_2 + \dots + w_n x_n + b z=w1x1+w2x2+⋯+wnxn+b

为了更简洁地表示，我们可以使用向量点积的形式：

z = w ⋅ x + b z = \mathbf{w} \cdot \mathbf{x} + b z=w⋅x+b

其中， w \mathbf{w} w 是一个包含所有权重的向量， x \mathbf{x} x 是一个包含所有输入的向量。

接着， z z z 会被送入一个非线性函数 σ \sigma σ（也就是我们后面要详细讲解的激活函数 ），产生最终的输出 a a a： a = σ ( z ) a = \sigma(z) a=σ(z)

这个 a a a 就是单个神经元的输出信号，它会作为下一个神经元的输入，或者成为网络的最终预测。

2.2 扩展到全连接层：矩阵运算的优雅

一个神经元显然不够，我们需要一整层的神经元协同工作。当一层中的每个神经元都与前一层的所有神经元相连接时，我们称之为全连接层（Fully Connected Layer）或密集层（Dense Layer）。

想象你的输入不再是单个 x x x，而是一个包含多个样本的批次（batch） 。例如，如果你有 m m m 张图片作为输入，每张图片有 n n n 个像素点。那么你的输入 X X X 就不是一个向量，而是一个矩阵，维度可能是 ( n , m ) (n, m) (n,m) 或 ( m , n ) (m, n) (m,n)。

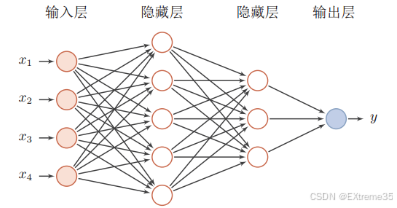
在这里，矩阵运算就派上了大用场，它能高效地并行计算一层中所有神经元对所有输入的处理过程：

输入矩阵 X X X ：假设我们的输入有 n i n n_{in} nin 个特征，同时处理 m m m 个样本，那么 X X X 的形状就是 ( n i n , m ) (n_{in}, m) (nin,m)。
权重矩阵 W W W ：如果当前层有 n o u t n_{out} nout 个神经元，每个神经元都有 n i n n_{in} nin 个权重，那么权重矩阵 W W W 的形状就是 ( n o u t , n i n ) (n_{out}, n_{in}) (nout,nin)。
偏置向量 b b b ：当前层有 n o u t n_{out} nout 个神经元，每个神经元一个偏置，所以 b b b 的形状是 ( n o u t , 1 ) (n_{out}, 1) (nout,1)。

现在，我们可以用更简洁的矩阵乘法来表示一整层的线性组合过程： Z = W X + b Z = W X + b Z=WX+b

这里的 Z Z Z 是当前层所有神经元对所有样本的线性组合结果，其形状为 ( n o u t , m ) (n_{out}, m) (nout,m)。

接着，我们对 Z Z Z 中的每一个元素应用激活函数 σ \sigma σ，得到当前层的输出 A A A： A = σ ( Z ) A = \sigma(Z) A=σ(Z)

A A A 的形状与 Z Z Z 相同，也是 ( n o u t , m ) (n_{out}, m) (nout,m)。这个 A A A 就是当前层的激活值矩阵 ，它将作为下一层的输入 X ( n e x t ) X^{(next)} X(next)。

【小提示】 ：矩阵乘法的顺序很重要！ ( W X ) (W X) (WX) 和 ( X W ) (X W) (XW) 是不同的。在这里，我们通常将 W W W 定义为 ( n o u t , n i n ) (n_{out}, n_{in}) (nout,nin)， X X X 定义为 ( n i n , m ) (n_{in}, m) (nin,m)，所以 W X W X WX 的结果是 ( n o u t , m ) (n_{out}, m) (nout,m)，正好与偏置 b b b 的形状 ( n o u t , 1 ) (n_{out}, 1) (nout,1) 匹配（广播机制会自动将 b b b 扩展为 ( n o u t , m ) (n_{out}, m) (nout,m) 进行加法）。

2.3 多层网络的链式传递：深度学习的"深"

神经网络之所以"深度"，就是因为它有多个这样的全连接层串联起来。一个层的输出 A ( l ) A^{(l)} A(l) 会成为下一层 l + 1 l+1 l+1 的输入 X ( l + 1 ) X^{(l+1)} X(l+1)，如此往复。

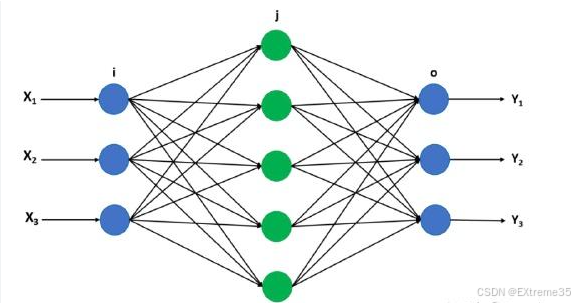
以一个上图神经网络为例（输入层、一个隐藏层、输出层）：

输入层 -> 隐藏层 1
- Z ( 1 ) = W ( 1 ) X + b ( 1 ) Z^{(1)} = W^{(1)} X + b^{(1)} Z(1)=W(1)X+b(1)
- A ( 1 ) = σ ( 1 ) ( Z ( 1 ) ) A^{(1)} = \sigma^{(1)}(Z^{(1)}) A(1)=σ(1)(Z(1)) （ A ( 1 ) A^{(1)} A(1) 现在是第一个隐藏层的输出）
隐藏层 1 -> 输出层
- Z ( 2 ) = W ( 2 ) A ( 1 ) + b ( 2 ) Z^{(2)} = W^{(2)} A^{(1)} + b^{(2)} Z(2)=W(2)A(1)+b(2)
- A ( 2 ) = σ ( 2 ) ( Z ( 2 ) ) A^{(2)} = \sigma^{(2)}(Z^{(2)}) A(2)=σ(2)(Z(2)) （ A ( 2 ) A^{(2)} A(2) 是最终的预测结果，通常用 Y ^ \hat{Y} Y^ 表示）

整个前向传播过程就是这样层层递进，将原始输入数据转化为越来越抽象、越来越有意义的特征表示，最终得到我们想要的预测值。

2.4 NumPy 实现一个 3 层网络的前向传播

理解了理论，我们现在用 Python 和 NumPy 来亲手实现这个前向传播过程。为了方便理解，我们会用一个类来封装。

python 复制代码

# 定义激活函数
def sigmoid(Z):
    """
    Sigmoid 激活函数
    Z: 任意形状的 NumPy 数组
    return: 经过 Sigmoid 激活后的数组
    """
    return 1 / (1 + np.exp(-Z))

def tanh(Z):
    """
    Tanh 激活函数
    Z: 任意形状的 NumPy 数组
    return: 经过 Tanh 激活后的数组
    """
    return np.tanh(Z)

def relu(Z):
    """
    ReLU 激活函数
    Z: 任意形状的 NumPy 数组
    return: 经过 ReLU 激活后的数组
    """
    return np.maximum(0, Z)

class SimpleNeuralNetwork:
    def __init__(self, layer_dims):
        """
        初始化神经网络的参数（权重 W 和偏置 b）。
        layer_dims: 一个列表，包含每一层的神经元数量。
                    例如：[2, 4, 1] 表示输入层2个神经元，隐藏层4个，输出层1个。
        """
        self.parameters = {}
        self.num_layers = len(layer_dims) # 神经网络的总层数（包括输入层，不包括输出层的激活函数层）

        # 遍历每一层，初始化权重和偏置
        # 注意：这里从第1层（隐藏层）开始，因为输入层没有权重和偏置
        for l in range(1, self.num_layers):
            # 权重矩阵 W(l) 的形状是 (当前层神经元数量, 前一层神经元数量)
            # 使用 He 初始化（适用于 ReLU），有助于缓解梯度消失问题
            self.parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * np.sqrt(2./layer_dims[l-1])
            
            # 偏置向量 b(l) 的形状是 (当前层神经元数量, 1)
            self.parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
            
            print(f"Layer {l} - W{l} shape: {self.parameters['W' + str(l)].shape}")
            print(f"Layer {l} - b{l} shape: {self.parameters['b' + str(l)].shape}")

    def forward_propagation(self, X):
        """
        执行前向传播过程。
        X: 输入数据，形状 (输入特征数, 样本数量)。
        return: 
            AL: 最后一层的激活值（即网络的预测输出）。
            caches: 一个列表，存储每层的 Z 和 A 值，用于反向传播。
        """
        caches = [] # 存储每层的中间计算结果，方便反向传播使用
        A = X # 当前层的激活值，最开始就是输入数据 X

        # 遍历所有隐藏层到输出层
        for l in range(1, self.num_layers): # 从第一隐藏层开始
            W = self.parameters['W' + str(l)]
            b = self.parameters['b' + str(l)]

            # 1. 线性组合：Z = W * A_prev + b
            Z = np.dot(W, A) + b
            
            # 2. 激活处理
            # 最后一层通常使用 Sigmoid (二分类) 或 Softmax (多分类)
            # 隐藏层通常使用 ReLU 或 Tanh
            if l == self.num_layers - 1: # 如果是最后一层
                A = sigmoid(Z) # 例如，对于二分类任务，输出层使用 Sigmoid
            else: # 如果是隐藏层
                A = relu(Z) # 隐藏层使用 ReLU
            
            # 将 Z 和 A 存入缓存，供反向传播使用
            caches.append({"Z": Z, "A_prev": A, "W":W, "b":b}) # 注意这里A_prev是当前层的A，下一次循环就成了前一层的A

        return A, caches # 返回最终输出和所有缓存

【代码解析】

__init__ 函数 ：在创建 SimpleNeuralNetwork 对象时被调用。它根据 layer_dims 初始化了所有层的权重 W 和偏置 b。
- 权重 W ：形状是 (当前层神经元数, 前一层神经元数)。我们使用 np.random.randn 生成随机数，并乘以 np.sqrt(2./layer_dims[l-1]) 进行初始化（这是一种常见的"He 初始化"方法，特别适合 ReLU 激活函数，可以帮助网络更快地收敛并避免梯度问题）。
- 偏置 b ：形状是 (当前层神经元数, 1)，初始化为零。
forward_propagation 函数 ：这是前向传播的核心。
- 它循环遍历网络的每一层。
- 在每一层中，它首先执行线性组合 Z = np.dot(W, A_prev) + b。A_prev 是前一层的输出，第一次循环时是网络的输入 X。
- 然后，它根据当前层的类型（隐藏层或输出层）应用不同的激活函数 。这里隐藏层用 relu，输出层用 sigmoid (因为XOR是二分类问题)。
- 它将每层的 Z 和 A_prev（当前层的激活值）以及 W 和 b 存储在 caches 列表中，这个缓存对后续的反向传播至关重要。

运行上面的代码，你会看到每一层权重和偏置的形状，以及第一次前向传播后，网络对 XOR 问题的预测结果。你会发现，由于权重是随机的，这个预测结果几乎是乱猜的，和真实标签 Y_xor 相去甚远。这就是为什么我们需要接下来的学习过程！

三、激活函数专题

在第二部分，我们简要提到了激活函数 σ ( z ) \sigma(z) σ(z)。现在，是时候深入了解这些赋予神经网络非凡能力的"小开关"了。它们决定了神经元在接收到输入后，是"兴奋"还是"抑制"，输出什么强度的信号。

3.1 为什么需要激活函数？

假设我们的神经网络完全没有激活函数，或者只使用线性激活函数（例如 a = z a = z a=z）。那么无论网络有多少层，它的最终输出都将仅仅是输入的一个线性组合。

例如，一个两层的网络：

A ( 1 ) = W ( 1 ) X + b ( 1 ) A^{(1)} = W^{(1)} X + b^{(1)} A(1)=W(1)X+b(1)

A ( 2 ) = W ( 2 ) A ( 1 ) + b ( 2 ) A^{(2)} = W^{(2)} A^{(1)} + b^{(2)} A(2)=W(2)A(1)+b(2)

将 A ( 1 ) A^{(1)} A(1) 代入 A ( 2 ) A^{(2)} A(2)：

A ( 2 ) = W ( 2 ) ( W ( 1 ) X + b ( 1 ) ) + b ( 2 ) A^{(2)} = W^{(2)} (W^{(1)} X + b^{(1)}) + b^{(2)} A(2)=W(2)(W(1)X+b(1))+b(2)

A ( 2 ) = ( W ( 2 ) W ( 1 ) ) X + ( W ( 2 ) b ( 1 ) + b ( 2 ) ) A^{(2)} = (W^{(2)} W^{(1)}) X + (W^{(2)} b^{(1)} + b^{(2)}) A(2)=(W(2)W(1))X+(W(2)b(1)+b(2))

你看，这最终仍然是一个 W e f f X + b e f f W_{eff} X + b_{eff} WeffX+beff 的形式，等价于一个单层线性网络。

这意味着，如果没有非线性激活函数，无论你堆叠多少层，网络都只能解决线性可分的问题（就像我们上面XOR问题中单层感知机的困境一样）。激活函数引入的非线性，是让神经网络能够学习和表示复杂模式的关键。

3.2 激活函数家族图谱：演进与选择

随着深度学习的发展，各种激活函数被提出、测试和优化。它们各有利弊，适用于不同的场景。我们可以把它们比喻为神经元的不同"性格"。

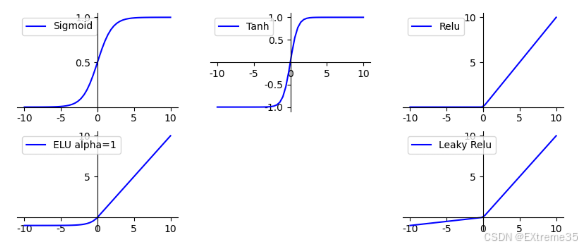
3.2.1 Sigmoid：保守型（将一切压到 0-1）

函数表达式 ： σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1+e^{-x}} σ(x)=1+e−x1
值域：(0, 1)
特点：
- 将任何实数输入压缩到 0 到 1 之间，非常适合作为二分类任务的输出层（因为可以解释为概率）。
- 历史意义：在早期神经网络中广泛使用，因为它有良好的数学特性，导数容易计算。
缺点：
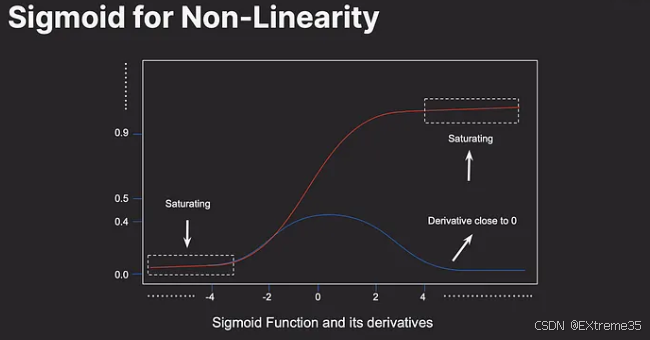
- 梯度消失问题 ：当输入 x x x 的绝对值很大时（无论是正无穷还是负无穷），Sigmoid 的梯度（导数）都会非常接近 0。
  
  d σ ( x ) d x = σ ( x ) ( 1 − σ ( x ) ) \frac{d\sigma(x)}{dx} = \sigma(x)(1 - \sigma(x)) dxdσ(x)=σ(x)(1−σ(x))
  
  它的最大导数只有 0.25（在 x = 0 x=0 x=0 处）。这意味着在反向传播时，梯度会变得非常小，导致深层网络的权重更新极其缓慢，甚至停滞，这就是**梯度消失（Vanishing Gradient）**问题。
- 输出非零均值：输出总是正的。这会导致下一层的输入总是同号，从而使得梯度更新时，权重只能向一个方向更新，效率较低。

3.2.2 Tanh ：平衡型（-1 到 1，均值 0）

函数表达式 ： tanh ⁡ ( x ) = e x − e − x e x + e − x \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} tanh(x)=ex+e−xex−e−x
值域：(-1, 1)
特点：
- 解决了 Sigmoid 输出非零均值的问题，其输出关于 0 对称。这通常会使得训练过程更快收敛。
- 在传统 RNN (循环神经网络) 中表现良好。
缺点：
- 依然存在梯度消失问题 ：当输入 x x x 的绝对值很大时，Tanh 的梯度同样会趋近于 0。它的最大导数是 1（在 x = 0 x=0 x=0 处），虽然比 Sigmoid 好，但仍无法彻底解决问题。

3.2.3 ReLU (Rectified Linear Unit)：激进型（要么活跃要么死亡）

函数表达式 ： ReLU ( x ) = max ⁡ ( 0 , x ) \text{ReLU}(x) = \max(0, x) ReLU(x)=max(0,x)
值域： [ 0 , ∞ ) [0, \infty) [0,∞)
特点：
- 革命性的突破：在深度学习领域取得了巨大成功，尤其是在卷积神经网络（CNN）中。
- 解决了梯度消失问题 ：当 x > 0 x > 0 x>0 时，梯度恒为 1，有效缓解了深层网络的梯度消失问题，使得训练能够更快、更深。
- 计算效率高：只需要一个简单的判断和赋值操作，计算速度远超 Sigmoid 和 Tanh（它们涉及指数运算）。
- 稀疏激活 ：当 x ≤ 0 x \le 0 x≤0 时，输出为 0。这使得一部分神经元被"关闭"，从而产生了稀疏激活性，有助于减少过拟合。
缺点：
- "死亡 ReLU"问题（Dying ReLU） ：当 x ≤ 0 x \le 0 x≤0 时，梯度恒为 0。这意味着如果一个神经元在训练过程中，其输入总是负数，那么它的权重将永远不会被更新，这个神经元就"死亡"了，永远不会被激活。这会限制网络的学习能力。

3.2.4 Leaky ReLU / ELU / Swish：现代解决方案

为了解决 ReLU 的"死亡"问题，同时保持其优势，研究人员提出了多种变体：

Leaky ReLU ：
- 当 x > 0 x > 0 x>0 时， LeakyReLU ( x ) = x \text{LeakyReLU}(x) = x LeakyReLU(x)=x
- 当 x ≤ 0 x \le 0 x≤0 时， LeakyReLU ( x ) = α x \text{LeakyReLU}(x) = \alpha x LeakyReLU(x)=αx （其中 α \alpha α 是一个很小的正数，比如 0.01）
- 特点：在负半区给了一个很小的斜率，确保梯度不会完全为 0，从而避免"死亡 ReLU"问题。
PReLU (Parametric ReLU) ：Leaky ReLU 的 α \alpha α 变成一个可学习的参数。
ELU (Exponential Linear Unit) ：
- 当 x > 0 x > 0 x>0 时， ELU ( x ) = x \text{ELU}(x) = x ELU(x)=x
- 当 x ≤ 0 x \le 0 x≤0 时， ELU ( x ) = α ( e x − 1 ) \text{ELU}(x) = \alpha (e^x - 1) ELU(x)=α(ex−1)
- 特点：在负半区有软饱和，可以解决 ReLU 的"死亡"问题，并且能让输出均值接近 0，类似于 Tanh，通常表现优于 Leaky ReLU。
Swish (Google Brain 提出)：
- Swish ( x ) = x ⋅ sigmoid ( x ) \text{Swish}(x) = x \cdot \text{sigmoid}(x) Swish(x)=x⋅sigmoid(x)
- 特点：一种自门控激活函数，在很多深度模型中表现优于 ReLU。它的特点是"平滑的非线性"，在负半区并非完全为零，而是在某个点开始下降，允许负梯度存在，有助于模型收敛。

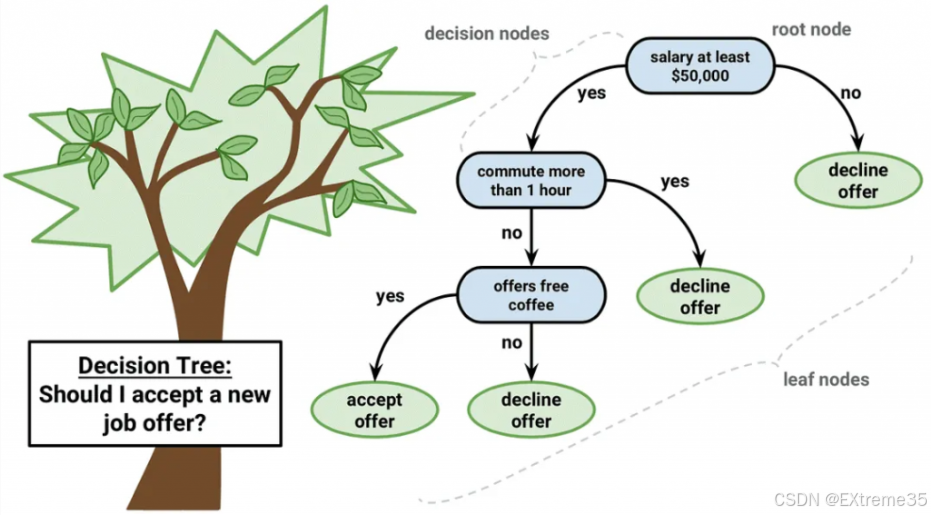
3.3 激活函数选择决策树

在实际应用中，如何选择激活函数呢？

特性	Sigmoid	Tanh	ReLU	Leaky ReLU/ELU/Swish
值域	(0, 1)	(-1, 1)	[ 0 , ∞ ) [0, \infty) [0,∞)	类似 ReLU，但避免死亡
梯度特性	易饱和，梯度消失	易饱和，梯度消失	非饱和，但可能死亡	非饱和，避免死亡
计算效率	低 (指数)	中 (指数)	高 (分段线性)	类似 ReLU，略高
输出均值	非零均值	零均值	非零均值	接近零均值 (ELU 更好)
常见使用场景	二分类输出层	传统 RNN 隐藏层	深度网络隐藏层首选	避免死亡 ReLU，性能优化

【快速测试】：

为什么说激活函数是让神经网络能够学习非线性模式的关键？
Sigmoid 和 Tanh 的主要缺点是什么？
ReLU 解决了什么问题？又引入了什么新问题？

【现代实践指南】

图像处理 (CNN) ：通常首选 ReLU 及其变体 (Leaky ReLU, ELU, Swish)。
序列处理 (RNN/LSTM/GRU) ：Tanh 在这些网络中依然有广泛应用，因为它能保持输出在较小的范围内，有助于稳定循环过程。
Transformer 模型（自然语言处理领域最前沿的模型）：通常使用 GELU (Gaussian Error Linear Unit)，因为它平滑且在负区域有非零梯度。
二分类输出层 ：Sigmoid。
多分类输出层 ：Softmax (将输出转化为概率分布)。

【深度思考】：Softmax 激活函数通常与交叉熵损失函数一起在多分类任务的输出层使用。它将一组任意实数（Logits）转换为一个概率分布，使得所有输出的概率之和为 1。它的公式为：

Softmax ( z i ) = e z i ∑ j = 1 K e z j \text{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}} Softmax(zi)=∑j=1Kezjezi

其中 K K K 是类别数量， z i z_i zi 是第 i i i 个类别的输入。

理解了激活函数，我们现在就拥有了前向传播的所有"零件"。但仅仅能计算出预测值是不够的，我们还需要知道如何根据这个预测值与真实值之间的差距，来调整网络内部的参数（权重 W W W 和偏置 b b b），让下一次的预测更准确。这就是反向传播的使命！

四、反向传播深度解析

如果把前向传播看作是"根据现有经验做决策"，那么反向传播（Backpropagation）就是"复盘与追责"。

当流水线末端产出了一个错误的结果（预测值与真实值不符），我们需要从后往前，顺着流水线找到每个工位（神经元）的负责人，告诉他们："因为你的参数设置偏差，导致了最终误差的 20 % 20\% 20%，请把你的权重往某个方向调一点。"

4.1 损失函数：量化"错误"的尺子

在追责之前，我们必须先定义什么是"错"。**损失函数（Loss Function）**就是用来衡量模型预测值 y ^ \hat{y} y^ 与真实标签 y y y 之间差距的指标。

对于回归问题，我们常用均方误差（MSE）：

L = 1 2 ( y ^ − y ) 2 L = \frac{1}{2}(\hat{y} - y)^2 L=21(y^−y)2

对于分类问题（如XOR），我们常用交叉熵损失（Cross-Entropy Loss）。

4.2 链式法则：梯度倒流的"交通规则"

反向传播的数学核心是微积分中的链式法则（Chain Rule）。

想象误差是一个信号，它要从损失函数 L L L 出发，逆着前向传播的路径流回去。我们要计算的是：损失函数 L L L 对某个权重 w w w 的导数 ∂ L ∂ w \frac{\partial L}{\partial w} ∂w∂L 。这个导数告诉我们：如果 w w w 增加一点点， L L L 会变大还是变小？变动的幅度有多大？

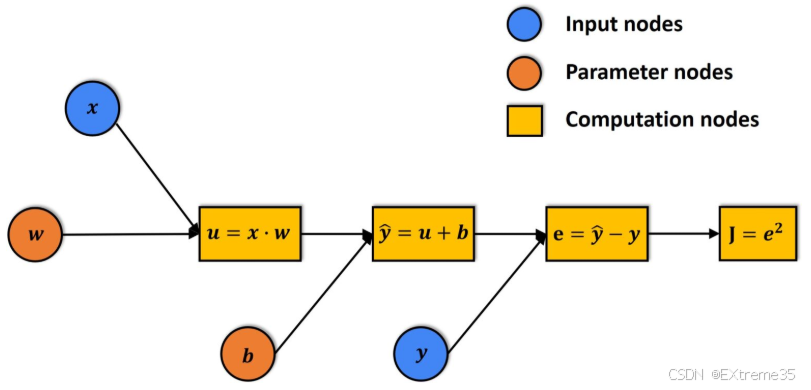
以输出层的一个神经元为例，我们要追究 W ( 2 ) W^{(2)} W(2) 的责任：

第一步： 损失对输出激活值的改变量 ∂ L ∂ A ( 2 ) \frac{\partial L}{\partial A^{(2)}} ∂A(2)∂L
第二步： 激活值对线性组合 Z Z Z 的改变量 ∂ A ( 2 ) ∂ Z ( 2 ) \frac{\partial A^{(2)}}{\partial Z^{(2)}} ∂Z(2)∂A(2)（这取决于激活函数的导数）
第三步： Z Z Z 对权重 W ( 2 ) W^{(2)} W(2) 的改变量 ∂ Z ( 2 ) ∂ W ( 2 ) \frac{\partial Z^{(2)}}{\partial W^{(2)}} ∂W(2)∂Z(2)（这等于前一层的输入 A ( 1 ) A^{(1)} A(1)）

根据链式法则，总责任（梯度）就是这三者的乘积：

∂ L ∂ W ( 2 ) = ∂ L ∂ A ( 2 ) ⋅ ∂ A ( 2 ) ∂ Z ( 2 ) ⋅ ∂ Z ( 2 ) ∂ W ( 2 ) \frac{\partial L}{\partial W^{(2)}} = \frac{\partial L}{\partial A^{(2)}} \cdot \frac{\partial A^{(2)}}{\partial Z^{(2)}} \cdot \frac{\partial Z^{(2)}}{\partial W^{(2)}} ∂W(2)∂L=∂A(2)∂L⋅∂Z(2)∂A(2)⋅∂W(2)∂Z(2)

4.3 权重更新：走下山谷

算出了梯度（方向和大小）后，我们就要更新权重了。这就是梯度下降法（Gradient Descent）。

W n e w = W o l d − η ⋅ ∂ L ∂ W W_{new} = W_{old} - \eta \cdot \frac{\partial L}{\partial W} Wnew=Wold−η⋅∂W∂L

这里的 η \eta η 是学习率（Learning Rate）。

如果 η \eta η 太大，步子迈得太大，可能会跨过山谷最低点，导致训练不稳定。
如果 η \eta η 太小，步子像蚂蚁爬，训练会慢得让人绝望。

五、常见陷阱与最佳实践

新手在构建网络时，往往会遇到"网络不收敛"或"准确率迷之不变"的情况。以下是五个最重要的实战建议：

5.1 权重初始化：打破对称性

不要全零初始化！ 如果 W W W 全是 0，隐藏层的所有神经元在第一轮计算出的梯度将完全相同。它们就像一群只会整齐划一做早操的机器人，永远学不到不同的特征。

推荐： 使用 np.random.randn(...) * 0.01 或者更专业的 Xavier 初始化。

5.2 梯度消失与爆炸

在深层网络中，如果权重太大，梯度会呈指数级增长（爆炸）；如果权重太小或用了太多 Sigmoid，梯度会消失。

现象： Loss 变成 NaN（爆炸）或者 Loss 长期不动（消失）。
应对： 隐藏层首选 ReLU ；使用 Batch Normalization（批归一化）。

5.3 学习率的选择

这是最重要的超参数。

技巧： 先尝试 0.1 0.1 0.1， 0.01 0.01 0.01， 0.001 0.001 0.001。观察 Loss 曲线。如果曲线震荡得厉害，调小它；如果下降得太慢，调大它。

5.4 始终先在小数据集上"过拟合"

这是一个非常高效的调试手段。拿 2-5 条数据喂给你的网络。如果你的网络连这几条数据都不能学到 100 % 100\% 100% 的准确率（Loss 降到几乎为 0），那么你的代码逻辑（公式推导或矩阵维度）一定有 Bug。

5.5 数值稳定性

计算 log(AL) 时，如果 AL 是 0，程序会崩溃。

实践： 永远给 log 里的值加上一个极小的常数：np.log(AL + 1e-15)。