双指针题目：两数之和 IV - 输入二叉搜索树

文章目录

• 题目
• • 标题和出处
  • 难度
  • 题目描述
  • • 要求
    • 示例
    • 数据范围
• 解法一
• • 思路和算法
  • 代码
  • 复杂度分析
• 解法二
• • 思路和算法
  • 代码
  • 复杂度分析
• 解法三
• • 思路和算法
  • 代码
  • 复杂度分析
• 解法四
• • 思路和算法
  • 代码
  • 复杂度分析

题目

标题和出处

标题：两数之和 IV - 输入二叉搜索树

出处：653. 两数之和 IV - 输入二叉搜索树

难度

3 级

题目描述

要求

给定一个二叉搜索树的根结点 root \texttt{root} root 和一个目标值 k \texttt{k} k，如果二叉搜索树中存在两个元素和等于给定的目标值，则返回 true \texttt{true} true。

示例

示例 1：

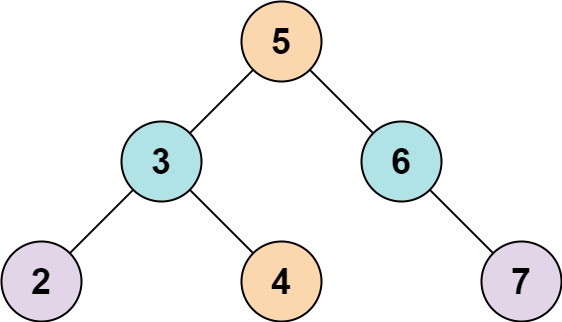
输入： root = [5,3,6,2,4,null,7], k = 9 \texttt{root = [5,3,6,2,4,null,7], k = 9} root = [5,3,6,2,4,null,7], k = 9

输出： true \texttt{true} true

示例 2：

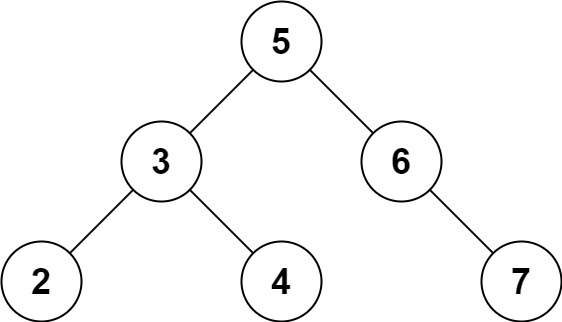
输入： root = [5,3,6,2,4,null,7], k = 28 \texttt{root = [5,3,6,2,4,null,7], k = 28} root = [5,3,6,2,4,null,7], k = 28

输出： false \texttt{false} false

数据范围

• 二叉搜索树的结点个数的范围是 [1, 10 4 ] \texttt{[1, 10}^\texttt{4}\texttt{]} [1, 104]
• -10 4 ≤ Node.val ≤ 10 4 \texttt{-10}^\texttt{4} \le \texttt{Node.val} \le \texttt{10}^\texttt{4} -104≤Node.val≤104
• 题目保证 root \texttt{root} root 是有效的二叉搜索树
• -10 5 ≤ k ≤ 10 5 \texttt{-10}^\texttt{5} \le \texttt{k} \le \texttt{10}^\texttt{5} -105≤k≤105

解法一

思路和算法

这道题要求判断给定的二叉搜索树中是否存在两个结点的结点值之和等于目标值 k k k。最直观的做法是遍历二叉搜索树中的所有结点，使用哈希集合存储已经遍历过的结点值。

具体做法是，从根结点开始，使用深度优先搜索遍历二叉搜索树，当遍历到每个结点时，执行如下操作。

1. 如果哈希集合中存在一个结点值等于 k k k 减去当前结点值，则找到两个结点的结点值之和等于目标值，返回 true \text{true} true。

2. 否则，将当前结点值添加到哈希集合中。

如果遍历结束之后仍未找到两个结点的结点值之和等于目标值，返回 false \text{false} false。

上述做法的核心思想是，假设二叉搜索树中有两个结点的结点值分别是 x x x 和 y y y 且 x + y = k x + y = k x+y=k，则这两个结点中一定有一个结点先被遍历到，该结点值会先加入哈希集合。假设值为 x x x 的结点先被遍历到，则当遍历到值为 y y y 的结点时， x x x 已经在哈希集合中，此时可以在哈希集合中找到 k − y = x k - y = x k−y=x，因此找到两个结点的结点值之和等于目标值。

代码

class Solution {
    Set<Integer> set = new HashSet<Integer>();

    public boolean findTarget(TreeNode root, int k) {
        if (root == null) {
            return false;
        }
        if (set.contains(k - root.val)) {
            return true;
        }
        set.add(root.val);
        return findTarget(root.left, k) || findTarget(root.right, k);
    }
}

复杂度分析

• 时间复杂度： O ( n ) O(n) O(n)，其中 n n n 是二叉搜索树的结点数。每个结点都被访问一次。

• 空间复杂度： O ( n ) O(n) O(n)，其中 n n n 是二叉搜索树的结点数。空间复杂度主要是栈空间，取决于二叉搜索树的高度，最差情况下二叉搜索树的高度是 O ( n ) O(n) O(n)。

解法二

思路和算法

也可以使用广度优先搜索遍历二叉搜索树，同样使用哈希集合存储已经遍历过的结点值，判断是否存在两个结点的结点值之和等于目标值。

代码

class Solution {
    public boolean findTarget(TreeNode root, int k) {
        Set<Integer> set = new HashSet<Integer>();
        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            if (set.contains(k - node.val)) {
                return true;
            }
            set.add(node.val);
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
        return false;
    }
}

复杂度分析

• 时间复杂度： O ( n ) O(n) O(n)，其中 n n n 是二叉搜索树的结点数。每个结点都被访问一次。

• 空间复杂度： O ( n ) O(n) O(n)，其中 n n n 是二叉搜索树的结点数。空间复杂度主要是队列空间，队列内元素个数不超过 n n n。

解法三

思路和算法

解法一和解法二都没有利用二叉搜索树的条件。利用二叉搜索树的性质，可以使用二叉搜索树的中序遍历寻找结点值。

根据二叉搜索树的性质可知，对于值为 x x x 的结点，值小于 x x x 的结点一定在值等于 x x x 的结点之前被访问，值大于 x x x 的结点一定在值等于 x x x 的结点之后被访问，因此二叉搜索树的中序遍历序列一定是递增的。得到二叉搜索树的中序遍历序列之后，即可使用「两数之和 II - 输入有序数组」的解法，判断是否存在两个结点的结点值之和等于目标值。

中序遍历的实现方式包括递归、迭代和莫里斯遍历，这里给出迭代实现。

迭代实现需要使用栈存储结点。从根结点开始遍历，遍历的终止条件是栈为空且当前结点为空。遍历的做法如下。

1. 如果当前结点不为空，则将当前结点入栈，然后将当前结点移动到其左子结点，重复该操作直到当前结点为空。

2. 将一个结点出栈，将当前结点设为出栈结点，将当前结点的结点值加入中序遍历序列。

3. 将当前结点移动到其右子结点。

4. 重复上述操作，直到达到遍历的终止条件。

得到二叉搜索树的中序遍历序列之后，可以使用二分查找或双指针的做法判断是否存在两个结点的结点值之和等于目标值，其中双指针的做法时间复杂度更低。双指针的做法如下。

用 left \textit{left} left 和 right \textit{right} right 表示两个指针，初始时 left \textit{left} left 和 right \textit{right} right 分别指向中序遍历序列的最小下标和最大下标。每次计算两个指针指向的结点值之和 sum \textit{sum} sum，比较 sum \textit{sum} sum 和目标值的大小关系，调整指针指向的下标。

• 如果 sum = k \textit{sum} = k sum=k，则找到两个结点的结点值之和等于目标值，返回 true \text{true} true。

• 如果 sum < k \textit{sum} < k sum<k，则将 left \textit{left} left 向右移动一位。

• 如果 sum > k \textit{sum} > k sum>k，则将 right \textit{right} right 向左移动一位。

上述操作的条件是 left < right \textit{left} < \textit{right} left<right。当 left = right \textit{left} = \textit{right} left=right 时，两个指针指向同一个结点值，因此不存在两个结点的结点值之和等于目标值，返回 false \text{false} false。

双指针的做法不会遗漏掉答案，理由如下。

假设存在指针 left k \textit{left}_k leftk 和 right k \textit{right}_k rightk 满足指针 left k \textit{left}_k leftk 和指针 right k \textit{right}_k rightk 指向的结点值之和等于目标值，则初始时一定有 left ≤ left k < right k ≤ right \textit{left} \le \textit{left}_k < \textit{right}_k \le \textit{right} left≤leftk<rightk≤right。如果初始时 left = left k \textit{left} = \textit{left}_k left=leftk 且 right = right k \textit{right} = \textit{right}_k right=rightk，则已经找到两个结点的结点值之和等于目标值。否则， left \textit{left} left 和 right \textit{right} right 一定有一个指针先到达答案指针，即 left \textit{left} left 先到达 left k \textit{left}_k leftk 或 right \textit{right} right 先到达 right k \textit{right}_k rightk。

• 如果 left \textit{left} left 先到达 left k \textit{left}_k leftk，则当 left \textit{left} left 到达 left k \textit{left}_k leftk 时， right > right k \textit{right} > \textit{right}_k right>rightk，此时两个结点的结点值之和大于目标值，因此一定是 right \textit{right} right 向左移动直到 right = right k \textit{right} = \textit{right}_k right=rightk。

• 如果 right \textit{right} right 先到达 right k \textit{right}_k rightk，则当 right \textit{right} right 到达 right k \textit{right}_k rightk 时， left < left k \textit{left} < \textit{left}_k left<leftk，此时两个结点的结点值之和小于目标值，因此一定是 left \textit{left} left 向右移动直到 left = left k \textit{left} = \textit{left}_k left=leftk。

代码

class Solution {
    public boolean findTarget(TreeNode root, int k) {
        List<Integer> traversal = new ArrayList<Integer>();
        Deque<TreeNode> stack = new ArrayDeque<TreeNode>();
        TreeNode node = root;
        while (!stack.isEmpty() || node != null) {
            while (node != null) {
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            traversal.add(node.val);
            node = node.right;
        }
        int left = 0, right = traversal.size() - 1;
        while (left < right) {
            int sum = traversal.get(left) + traversal.get(right);
            if (sum == k) {
                return true;
            } else if (sum > k) {
                right--;
            } else {
                left++;
            }
        }
        return false;
    }
}

复杂度分析

• 时间复杂度： O ( n ) O(n) O(n)，其中 n n n 是二叉树的结点数。每个结点都被访问一次。

• 空间复杂度： O ( n ) O(n) O(n)，其中 n n n 是二叉树的结点数。空间复杂度主要是栈空间和中序遍历序列空间，栈空间取决于二叉树的高度，最差情况下二叉树的高度是 O ( n ) O(n) O(n)，中序遍历序列需要 O ( n ) O(n) O(n) 的空间存储全部结点值。

解法四

思路和算法

解法三虽然利用了二叉搜索树的性质，但是做法是首先得到中序遍历序列，然后在中序遍历序列上使用双指针的做法判断是否存在两个结点的结点值之和等于目标值，中序遍历序列需要 O ( n ) O(n) O(n) 的空间。其实，这道题不需要得到中序遍历序列，而是可以使用结点代替中序遍历序列中的双指针。使用 left \textit{left} left 和 right \textit{right} right 分别表示双指针结点，其中 left \textit{left} left 模拟正向中序遍历操作， right \textit{right} right 模拟反向中序遍历操作。正向中序遍历依次遍历左子树、根结点、右子树，反向中序遍历依次遍历右子树、根结点、左子树。

为了模拟正向中序遍历操作和反向中序遍历操作，需要分别创建两个栈用于存储对应的结点，正向中序遍历对应的栈为左侧栈，反向中序遍历对应的栈为右侧栈。

模拟正向中序遍历操作和反向中序遍历操作可以基于中序遍历的迭代实现。将 left \textit{left} left 和 right \textit{right} right 从根结点开始，定位到二叉搜索树中的最左侧结点和最右侧结点，做法如下。

1. 如果 left \textit{left} left 不为空，则将 left \textit{left} left 入左侧栈，然后将 left \textit{left} left 移动到其左子结点，重复该操作直到 left \textit{left} left 为空。

2. 如果 right \textit{right} right 不为空，则将 right \textit{right} right 入右侧栈，然后将 right \textit{right} right 移动到其右子结点，重复该操作直到 right \textit{right} right 为空。

此时 left \textit{left} left 和 right \textit{right} right 分别为二叉搜索树中的最左侧结点和最右侧结点，可以模拟正向中序遍历操作和反向中序遍历操作，使用双指针判断是否存在两个结点的结点值之和等于目标值。双指针的做法如下。

1. 将 left \textit{left} left 和 right \textit{right} right 分别取左侧栈和右侧栈的栈顶结点，计算 left \textit{left} left 和 right \textit{right} right 的结点值之和 sum \textit{sum} sum。

2. 比较 sum \textit{sum} sum 和目标值的大小关系，调整指针。

   • 如果 sum = k \textit{sum} = k sum=k，则找到两个结点的结点值之和等于目标值，返回 true \text{true} true。

   • 如果 sum < k \textit{sum} < k sum<k，则在左侧栈中定位到正向中序遍历的下一个结点。

   • 如果 sum > k \textit{sum} > k sum>k，则在右侧栈中定位到反向中序遍历的下一个结点。

在左侧栈中定位到正向中序遍历的下一个结点的做法如下。

1. 将左侧栈的一个结点出栈，将当前结点设为出栈结点的右子结点。

2. 将当前结点入左侧栈，然后将当前结点移动到其左子结点，重复该操作直到当前结点为空。

在右侧栈中定位到反向中序遍历的下一个结点的做法如下。

1. 将右侧栈的一个结点出栈，将当前结点设为出栈结点的左子结点。

2. 将当前结点入右侧栈，然后将当前结点移动到其右子结点，重复该操作直到当前结点为空。

双指针操作的条件是两个栈都不为空且 left ≠ right \textit{left} \ne \textit{right} left=right。当至少有一个栈为空或 left = right \textit{left} = \textit{right} left=right 时，不存在两个结点的结点值之和等于目标值，返回 false \text{false} false。

代码

class Solution {
    public boolean findTarget(TreeNode root, int k) {
        Deque<TreeNode> leftStack = new ArrayDeque<TreeNode>();
        Deque<TreeNode> rightStack = new ArrayDeque<TreeNode>();
        TreeNode left = root, right = root;
        while (left != null) {
            leftStack.push(left);
            left = left.left;
        }
        while (right != null) {
            rightStack.push(right);
            right = right.right;
        }
        while (!leftStack.isEmpty() && !rightStack.isEmpty() && leftStack.peek() != rightStack.peek()) {
            left = leftStack.peek();
            right = rightStack.peek();
            int sum = left.val + right.val;
            if (sum == k) {
                return true;
            } else if (sum < k) {
                TreeNode node = leftStack.pop().right;
                while (node != null) {
                    leftStack.push(node);
                    node = node.left;
                }
            } else {
                TreeNode node = rightStack.pop().left;
                while (node != null) {
                    rightStack.push(node);
                    node = node.right;
                }
            }
        }
        return false;
    }
}

复杂度分析

• 时间复杂度： O ( n ) O(n) O(n)，其中 n n n 是二叉树的结点数。每个结点都被访问一次。

• 空间复杂度： O ( n ) O(n) O(n)，其中 n n n 是二叉树的结点数。空间复杂度主要是栈空间，取决于二叉树的高度，最差情况下二叉树的高度是 O ( n ) O(n) O(n)。虽然最差空间复杂度和解法三相同，但是平均情况下的空间复杂度是 O ( log ⁡ n ) O(\log n) O(logn)，优于解法三的平均空间复杂度。