机器学习线性回归

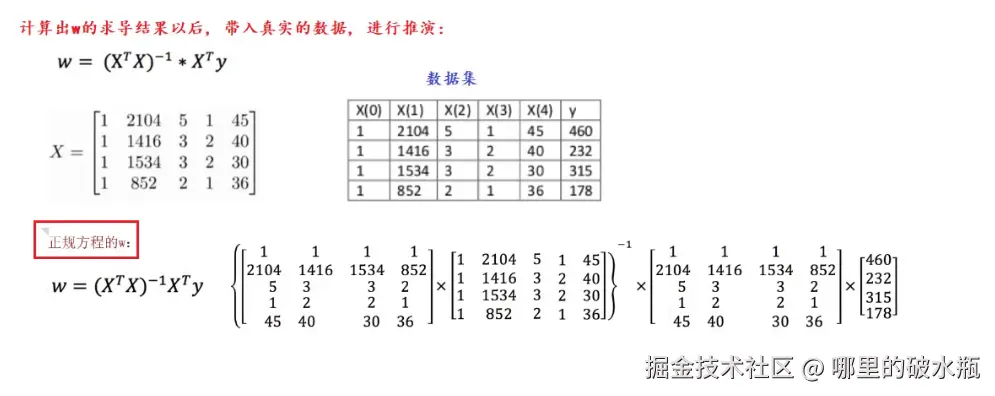
线性回归

回归问题：目标是预测连续数值（体重），而不是分类标签

术语：

自变量（特征）
因变量（目标）

比如，已知身高，求体重，这里，体重是因变量 ，身高是自变量。

K：斜率（weight 权重）
X：自变量
b：截距（bias 偏置）

公式是： <math xmlns="http://www.w3.org/1998/Math/MathML"> Y = k X + b Y = kX + b </math>Y=kX+b，这只是一元线程回归

我们需要算出来，斜率是多少，截距是多少

回归方程函数

为什么还有这个公式呢，因为正常情况下不可能只有一个特征。

这 T 表示 k 的转置（把列向量变成行向量，用于点积）

公式： <math xmlns="http://www.w3.org/1998/Math/MathML"> y = k x + b y = k^x + b </math>y=kx+b

公式的由来

假设已知有多个特征，如下，所以一元线程回归

所以变成了如下：

<math xmlns="http://www.w3.org/1998/Math/MathML"> y = k 1 x 1 + k 2 x 2 + ⋅ ⋅ ⋅ + k n x n + b y = k_{1}x_{1} + k_{2}x_{2} + ··· + k_{n}x_{n} + b </math>y=k1x1+k2x2+⋅⋅⋅+knxn+b

如何把 b 截距引进来的，所以要在最开始加一个 w0，表示截距b，x0 用 1 表示。这样再实现矩阵相乘就可以了。
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> k = [ k 0 k 1 k 2 ⋮ k n ] , x = [ x 0 x 1 x 2 ⋮ x n ] \boldsymbol{k} = \begin{bmatrix} k_0 \\ k_1 \\ k_2 \\ \vdots \\ k_n \end{bmatrix}, \quad \boldsymbol{x} = \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} </math>k= k0k1k2⋮kn ,x= x0x1x2⋮xn

线性回归案例：

钢轨伸缩长度与温度
昆虫鸣叫次数与天气
国内GDP与双十一销售额

线性回归API

py 复制代码

from sklearn.linear_model import LinearRegression

# 案例基于身高，预测体重

# 1. 获取数据
x_train = [[160], [166], [172], [174], [180]]
y_train = [56.3, 60.6, 65.1, 68.5, 75]

x_test = [[176]]

# 2. 数据预处理
# 3. 特征工程

# 4. 模型训练
# 创建回归模型
estimator = LinearRegression()
estimator.fit(x_train, y_train)

# 5. 模型预测
y_predict = estimator.predict(x_test)
print(y_predict) # 70.3047619

# 6. 模型评估
# 斜率
print(estimator.coef_) # 0.92942177
# 截距
print(estimator.intercept_) # -93.27346938775517

这里不画拟合回归线。

损失函数

上面我们能得知，用API生成一条拟合回归线。

我们一眼能看出红色的直线。但是这个线是怎么求出来的呢？

是通过：误差 = 预测值 - 真实值，越小越好

所以需要损失函数，衡量每个样本的预测值与真实值效果的函数，也叫代价函数、成本函数、目标函数

更好的拟合所有的点，也就是误差最小，误差和最小

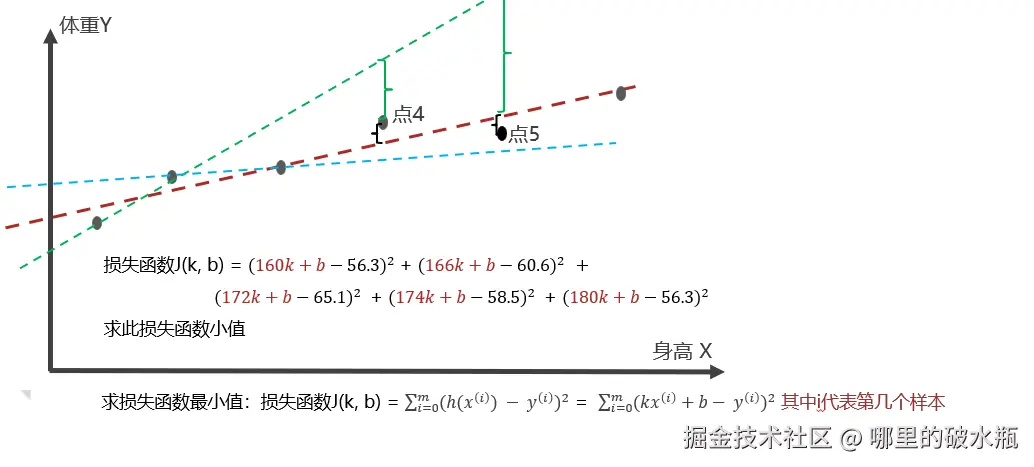
损失函数计算方式

我们来计算出来，斜率（权重）和截距（偏置）

损失函数：用来描述每个样本值和预测值之间的关系的
误差 = 预测值 - 真实值

已知：

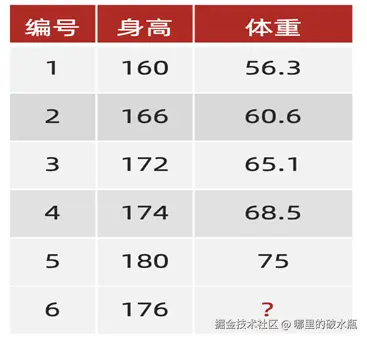
拿点5 举例子

kx + b
代入 = 180k + b
再减去真实值 = 180k + b - 75

得出公式是： <math xmlns="http://www.w3.org/1998/Math/MathML"> k x + b − y kx + b - y </math>kx+b−y，其中 y 是真实值。

注意下图：w 其实是 k，这里写错了

这样计算之后，可能有的结果是正的，有的结果是负的。

所以又分为三种计算方式

最小二乘：每个样本的误差值的平方和
均方误差：最小二乘 / 样本数
平均绝对值误差：每个样本的误差的绝对值的平均值

最小二乘解法如下

根据上面的例子

<math xmlns="http://www.w3.org/1998/Math/MathML"> 损失函数 L ( k , b ) = ( 160 k + b − 56.3 ) 2 + ( 166 k + b − 60.6 ) 2 + ( 172 k + b − 65.1 ) 2 + ( 174 k + b − 68.5 ) 2 + ( 180 k + b − 75 ) 2 损失函数L(k,b) = (160k + b - 56.3)^2 + (166k + b - 60.6)^2 + (172k + b - 65.1)^2 + (174k + b - 68.5)^2 + (180k + b - 75)^2 </math>损失函数L(k,b)=(160k+b−56.3)2+(166k+b−60.6)2+(172k+b−65.1)2+(174k+b−68.5)2+(180k+b−75)2

为了简便运算，这里先固定 b = -100

于是公式变成了如下：

<math xmlns="http://www.w3.org/1998/Math/MathML"> 损失函数 L ( k , b = − 100 ) = ( 160 k + ( − 100 ) − 56.3 ) 2 + ( 166 k + ( − 100 ) − 60.6 ) 2 + ( 172 k + ( − 100 ) − 65.1 ) 2 + ( 174 k + ( − 100 ) − 68.5 ) 2 + ( 180 k + ( − 100 ) − 75 ) 2 损失函数L(k,b = -100) = (160k + (-100) - 56.3)^2 + (166k + (-100) - 60.6)^2 + (172k + (-100) - 65.1)^2 + (174k + (-100) - 68.5)^2 + (180k + (-100) - 75)^2 </math>损失函数L(k,b=−100)=(160k+(−100)−56.3)2+(166k+(−100)−60.6)2+(172k+(−100)−65.1)2+(174k+(−100)−68.5)2+(180k+(−100)−75)2

我们先计算这一小块

已知： <math xmlns="http://www.w3.org/1998/Math/MathML"> ( 160 k + ( − 100 ) − 56.3 ) 2 (160k + (-100) - 56.3)^2 </math>(160k+(−100)−56.3)2

合并常数项 = <math xmlns="http://www.w3.org/1998/Math/MathML"> ( 160 k − 156.3 ) 2 (160k - 156.3)^2 </math>(160k−156.3)2

此时我们发现 这就是 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( a − b 2 ) (a - b^2) </math>(a−b2) = <math xmlns="http://www.w3.org/1998/Math/MathML"> a 2 − 2 a b + b 2 a^2 - 2ab + b^2 </math>a2−2ab+b2

这是完全平方公式哈。

继续计算

<math xmlns="http://www.w3.org/1998/Math/MathML"> = ( 160 k − 156.3 ) 2 + ( 166 k − 160.6 ) 2 + ( 172 k − 165.1 ) 2 + ( 174 k − 168.5 ) 2 + ( 180 k − 175 ) 2 = (160k - 156.3)^2 + (166k -160.6)^2 + (172k -165.1)^2 + (174k -168.5)^2 + (180k -175)^2 </math>=(160k−156.3)2+(166k−160.6)2+(172k−165.1)2+(174k−168.5)2+(180k−175)2

<math xmlns="http://www.w3.org/1998/Math/MathML"> = ( ( 160 k ) 2 − 2 ∗ 160 k ∗ 156.3 + 156. 3 2 ) + ( ( 166 k ) 2 − 2 ∗ 166 k ∗ 160.6 + 160. 6 2 ) + ( ( 172 k ) 2 − 2 ∗ 172 k ∗ 165.1 + 165. 1 2 ) + ( ( 174 k ) 2 − 2 ∗ 174 k ∗ 168.5 + 168. 5 2 ) + ( ( 180 k ) 2 − 2 ∗ 180 k ∗ 175 + 17 5 2 ) = ((160k)^2 - 2 * 160k * 156.3 + 156.3^2) + ((166k)^2 - 2 * 166k * 160.6 + 160.6^2) + ((172k)^2 - 2 * 172k * 165.1 + 165.1^2) + ((174k)^2 - 2 * 174k * 168.5 + 168.5^2) + ((180k)^2 - 2 * 180k * 175 + 175^2) </math>=((160k)2−2∗160k∗156.3+156.32)+((166k)2−2∗166k∗160.6+160.62)+((172k)2−2∗172k∗165.1+165.12)+((174k)2−2∗174k∗168.5+168.52)+((180k)2−2∗180k∗175+1752)

下面我用第一个演示一下，每一个都要计算，有点多

分别计算 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( ( 160 k ) 2 − 2 ∗ 160 k ∗ 156.3 + 156. 3 2 ) ((160k)^2 - 2 * 160k * 156.3 + 156.3^2) </math>((160k)2−2∗160k∗156.3+156.32) 的平方项、一次项、常数项

平方项 = <math xmlns="http://www.w3.org/1998/Math/MathML"> 160 ∗ 160 ∗ k 2 = 25600 k 2 160 * 160 * k^2 = 25600k^2 </math>160∗160∗k2=25600k2
一次项 = <math xmlns="http://www.w3.org/1998/Math/MathML"> − 2 ∗ 160 ∗ 156.3 ∗ k = − 50016 k -2 * 160 * 156.3 * k = -50016k </math>−2∗160∗156.3∗k=−50016k
常数项 = <math xmlns="http://www.w3.org/1998/Math/MathML"> 156.3 ∗ 156.3 = 24 , 429.69 156.3 * 156.3 = 24,429.69 </math>156.3∗156.3=24,429.69

所以等于 <math xmlns="http://www.w3.org/1998/Math/MathML"> = 25600 k − 50016 k + 24429.69 = 25600k - 50016k + 24429.69 </math>=25600k−50016k+24429.69

但是这里是不能直接这样的，要把所有的项目合起来，平方项、一次项、常数项相加，最后计算。

一共五个数据点计算后
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> = 25600 k 2 − 50016 k + 24429.69 = 27556 k 2 − 53319.2 k + 25792.36 = 29584 k 2 − 56794.4 k + 27258.01 = 30276 k 2 − 58638 k + 28392.25 = 32400 k 2 − 63000 k + 302625 \begin{align*} &= 25600k^2 - 50016k + 24429.69 \\ &= 27556k^2 - 53319.2k + 25792.36 \\ &= 29584k^2 - 56794.4k + 27258.01 \\ &= 30276k^2 - 58638k + 28392.25 \\ &= 32400k^2 - 63000k + 302625 \\ \end{align*} </math>=25600k2−50016k+24429.69=27556k2−53319.2k+25792.36=29584k2−56794.4k+27258.01=30276k2−58638k+28392.25=32400k2−63000k+302625

平方项、一次项、常数项的总结果 = <math xmlns="http://www.w3.org/1998/Math/MathML"> 145 , 416 k 2 − 281 , 767.6 k + 408 , 497.31 145,416k^2 - 281,767.6k + 408,497.31 </math>145,416k2−281,767.6k+408,497.31

计算 K 值

<math xmlns="http://www.w3.org/1998/Math/MathML"> k = − ( − 281 , 767.6 ) / ( 2 ∗ 145 , 416 ) = 0.968832865709413 k = -(-281,767.6) / (2*145,416) = 0.968832865709413 </math>k=−(−281,767.6)/(2∗145,416)=0.968832865709413

<math xmlns="http://www.w3.org/1998/Math/MathML"> 或者直接： 281767.6 / 2 / 145416 或者直接：281767.6 / 2 / 145416 </math>或者直接：281767.6/2/145416

总结

缺点：当样本点比较多的时候，值会非常大。

总结

最小二乘

每个样本的误差值的平方和

<math xmlns="http://www.w3.org/1998/Math/MathML"> 损失函数 J ( w , b ) = ∑ i = 0 m ( h ( x ( i ) ) − y ( i ) ) 2 损失函数J(w,b) = \sum_{i=0}^m(h(x^{(i)}) - y^{(i)})^2 </math>损失函数J(w,b)=∑i=0m(h(x(i))−y(i))2

均方误差 (Mean-Square Error, MSE)

每个样本的误差值的平方和的平均值

方块圈住的就是最小二乘

i 表示具体的第几个样本

<math xmlns="http://www.w3.org/1998/Math/MathML"> 损失函数 J ( w , b ) = 1 m ∑ i = 0 m ( h ( x ( i ) ) − y ( i ) ) 2 损失函数J(w,b) = \frac{1}{m}\sum_{i=0}^m(h(x^{(i)}) - y^{(i)})^2 </math>损失函数J(w,b)=m1∑i=0m(h(x(i))−y(i))2

平均绝对值误差 (Mean Absolute Error , MAE)

每个样本的误差值的绝对值的和的平均值

<math xmlns="http://www.w3.org/1998/Math/MathML"> 损失函数 J ( w , b ) = 1 m ∑ 0 m ∣ h ( x ( i ) ) − y ( i ) ∣ 损失函数J(w,b) = \frac{1}{m}\sum_{0}^m \left| h(x^{(i)}) - y^{(i)} \right| </math>损失函数J(w,b)=m1∑0m h(x(i))−y(i)

线性回归问题求解需要什么？

损失函数越小，越好

损失函数可用来描述输出（预测值）和观测结果（真实值）效果，可衡量模型效果好坏
不同的任务比如分类、回归、聚类问题，一般会采用各自的损失函数
线性回归求解一般需要数据、假设函数、损失函数、损失函数优化方法等部分，相互配合共同完成

复习

复习导数

当函数 𝑦=𝑓(𝑥) 的自变量 𝑥 在一点 <math xmlns="http://www.w3.org/1998/Math/MathML"> 𝑥 0 𝑥_0 </math>x0 上产生一个增量 Δ𝑥 时，函数输出值的增量 Δ𝑦 与自变量增量 Δ𝑥 的比值在 Δ𝑥 趋于0 时的极限 𝐴 如果存在，𝐴 即为在 𝑥 处的导数，记作 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ′ ( x o ) f'(x_o) </math>f′(xo)

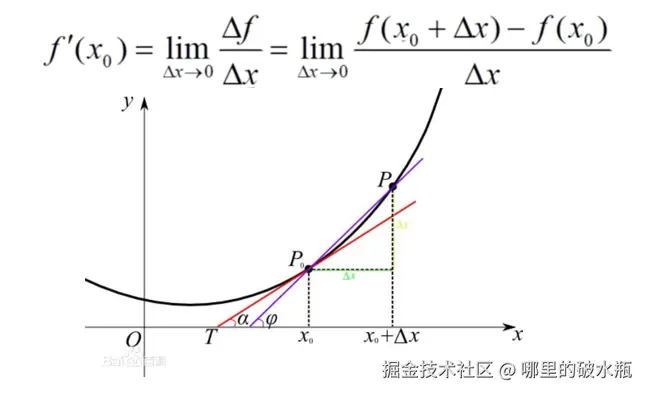
导数的几何意义

函数 y=f(x) 在点 <math xmlns="http://www.w3.org/1998/Math/MathML"> x 0 x_0 </math>x0 处的导数的几何意义，就是曲线 y=f(x) 在点 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( x 0 , f ( x 0 ) ) P(x_0,f(x_0)) </math>P(x0,f(x0)) 处的切线的斜率，即曲线 y=f(x) 在 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( x 0 , f ( x 0 ) ) P(x_0, f(x_0)) </math>P(x0,f(x0))处的切线的斜率是f'(x_0)。

常见函数的导数

导数的四则运算

直接套公式

第二个我说一下，公式是， (a * b)' = a' * b + a * b'

第四个 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( e 2 x ) ′ (e^{2x})' </math>(e2x)′

= 带入公式， <math xmlns="http://www.w3.org/1998/Math/MathML"> e x e^x </math>ex 的导还是 <math xmlns="http://www.w3.org/1998/Math/MathML"> e x e^x </math>ex，所以 <math xmlns="http://www.w3.org/1998/Math/MathML"> e 2 x e^{2x} </math>e2x = <math xmlns="http://www.w3.org/1998/Math/MathML"> e 2 x e^{2x} </math>e2x
= 求2x的导，还是 2 = <math xmlns="http://www.w3.org/1998/Math/MathML"> 2 e 2 x 2e^{2x} </math>2e2x

题

举个例子:计算该函数y = 〖"(" 𝑥^2 "+2x)" 〗^2 的导函数

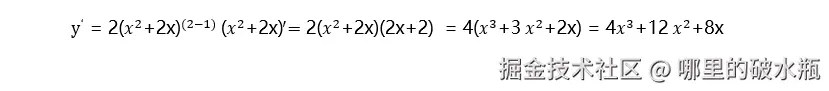
偏导

导数求极值

导数为0的位置是函数的极值点

求函数 <math xmlns="http://www.w3.org/1998/Math/MathML"> y = 𝑥 2 − 4 x + 5 y = 𝑥^2 - 4x + 5 </math>y=x2−4x+5 的极小值

求导法：对x求导，令导数

= <math xmlns="http://www.w3.org/1998/Math/MathML"> 0 ： y ′ = 2 x − 4 = 0 0：y' = 2x - 4 = 0 </math>0：y′=2x−4=0
x = 2
将 x = 2 带入，4 - 8 + 5 = 1
所以y极小值 = 1

多变量导数求解

Z是关于 x 和 y 的函数记成 <math xmlns="http://www.w3.org/1998/Math/MathML"> z ( x , y ) z(x,y) </math>z(x,y)，求解 <math xmlns="http://www.w3.org/1998/Math/MathML"> z = ( 𝑥 − 2 ) 2 + ( 𝑦 − 3 ) 2 z = (𝑥−2)^2 + (𝑦−3)^2 </math>z=(x−2)2+(y−3)2 的极小值

这题要同时求 x 和 y 的两个未知数，所以思路是，先把 x 和 y 同时解出来，方式就是乘法法则

首先先计算x，此时 y - 3² = 0

(x - 2)²
(x - 2)' * (x - 2)'
(x - 2)' * (x - 2) + (x - 2) * (x - 2)'
1 * (x - 2) + (x - 2) * 1
(x - 2) + (x - 2)
x - x = 2x，-2-2 = -4
2x - 4
2(x - 2) = 0
两边除以 2 = x - 2 = 0
x = 2

计算 y，此时 x - 2² = 0

(y - 3)²
(y - 3)'(y - 3) + (y - 3)(y - 3)'
(y - 3) + (y - 3)
2y - 6
2(y - 3)
y - 3 = 0
y = 3

上面的有些复杂

例子： <math xmlns="http://www.w3.org/1998/Math/MathML"> Z = x 2 + 2 x y − 3 y 2 Z = x^2 + 2xy - 3y^2 </math>Z=x2+2xy−3y2

x = 2x + 2y（3y²是常数）
y = 2x - 6y（x2是常数）

向量和矩阵

向量运算

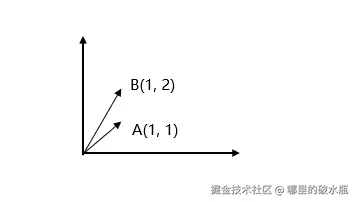
向量是有大小和方向

几何意义上表示：向量(1,1), 向量（1,2）

向量基运算

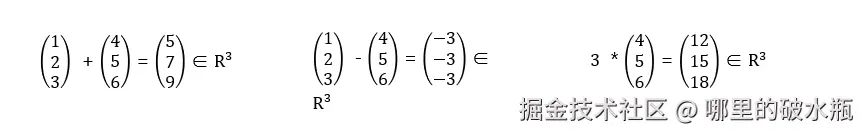
向量矩阵转置 Transpose

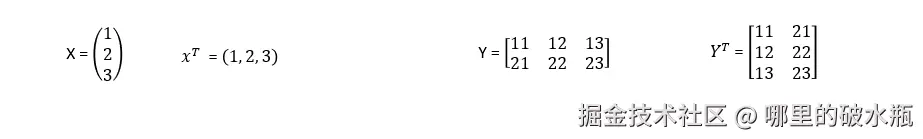
范数Norm

范数(norm)是数学中的一种基本概念，具有长度的意义

1范数(L1范数)-向量中各个元素绝对值之和
2范数(L2范数)-向量的模长，每个元素平方求和，再开平方根
p-范数：向量中每一个元素p幂求和，在开p次根

L1范数

<math xmlns="http://www.w3.org/1998/Math/MathML"> 𝑥 𝑇 = ( 1 , 2 , − 3 ) ‖ x ‖ 1 = ∣ 1 ∣ + ∣ 2 ∣ + ∣ − 3 ∣ = 6 𝑥^𝑇 = (1, 2, −3) ‖x‖_1 = |1| + |2| + |−3| = 6 </math>xT=(1,2,−3)‖x‖1=∣1∣+∣2∣+∣−3∣=6

L2范数

<math xmlns="http://www.w3.org/1998/Math/MathML"> 𝑥 𝑇 = ( 1 , 2 , − 3 ) ∣ ∣ x ∣ ∣ 2 = 2 1 12 + 2 2 + ( − 3 ) 2 = √ 14 𝑥^𝑇=(1, 2, −3) ||x||_2 = 2\sqrt{1^{12} + 2^2 + (-3)^2} = √14 </math>xT=(1,2,−3)∣∣x∣∣2=2112+22+(−3)2 =√14

<math xmlns="http://www.w3.org/1998/Math/MathML"> 𝑥 𝑇 = ( 1 , 2 , − 3 ) 𝑥^𝑇=(1,2,−3) </math>xT=(1,2,−3)

注意：向量的转置@向量

<math xmlns="http://www.w3.org/1998/Math/MathML"> 𝑥 𝑇 x = 1 2 + 2 2 + ( − 3 ) 2 = 14 𝑥^𝑇x=1^2+2^2+(−3)^2 = 14 </math>xTx=12+22+(−3)2=14

X为向量： <math xmlns="http://www.w3.org/1998/Math/MathML"> 𝑥 𝑇 x 与 ∣ ∣ x ∣ ∣ 2 2 𝑥^𝑇x 与||x||_2^2 </math>xTx与∣∣x∣∣22 是一样的

Lp范数：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> ∥ x ∥ p = ( ∣ x 1 ∣ p + ∣ x 2 ∣ p + ⋯ + ∣ x n ∣ p ) 1 p \|x\|_p = \left( |x_1|^p + |x_2|^p + \cdots + |x_n|^p \right)^{\frac{1}{p}} </math>∥x∥p=(∣x1∣p+∣x2∣p+⋯+∣xn∣p)p1

矩阵 Matrix 1

矩阵是数学中的一种基本概念，表达m行n列的数据等

矩阵在机器学习中的表达

矩阵加法

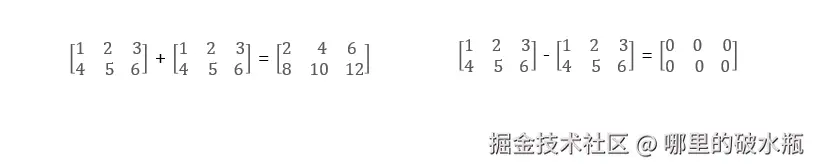
总结：用 A 的每一行，都要乘以 B 的每一列。

矩阵乘法：对应行列元素相乘，然后再加和再一起

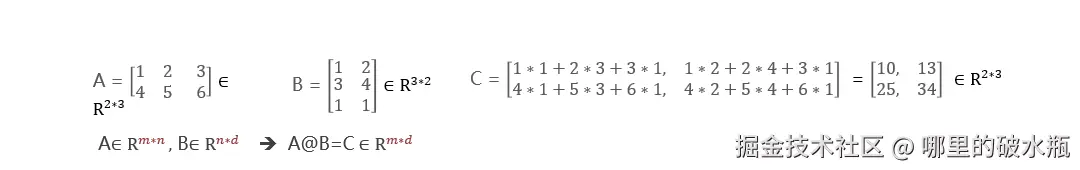
术语：

方阵：行列数一样
对称方阵：一种特殊的方阵，沿着主对角线，其元素对称 aij = aji

可以发现，1，2 的元素是2，2，1 的元素也是 2

单位阵：一种特殊的方阵，用符号E或者是I来表示

特点：对角线为 1 其他为 0

矩阵乘法的性质

矩阵的逆

例子：通过 A 和 I 求出 B

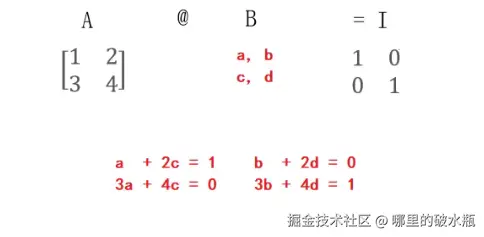
已知结果是

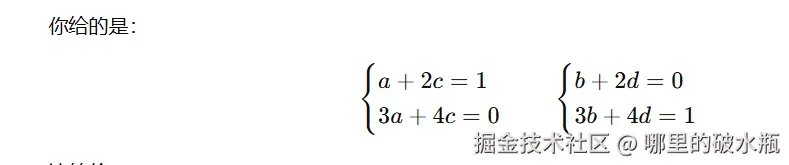
等价于如下图

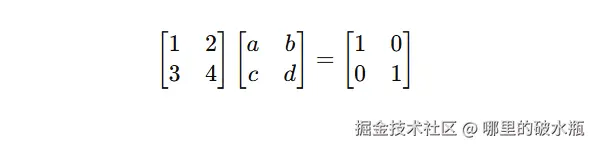
此时我们可以求解出 ac，bd 等于多少。

求 C 结果如下：

a + 2c = 1

3a + 4c = 0

首先根据 a + 2c = 1，可以改成 a = 1 - 2c

将a = 1 - 2c 代入 3a + 4c = 0

= 3(1 - 2c) + 4c = 0
= 3 - 6c + 4c = 0
合并同类项
-6c + 4c = -2c
3 - 2c = 0

解C：

3 - 2c = 0
得知：3 - 2(3/2) = 0
3 - 3 = 0
c = 1.5

求 a 结果如下

a = 1 - 2c
a = 1 - 2 * 1.5
a = -2

总结

矩阵转置的性质

损失函数最小值求法

正规方程法

前面我们要知道，通过最小二乘，可以计算出如下

现在我们将来计算 B 的值

例子：

一元线性回归损失函数 <math xmlns="http://www.w3.org/1998/Math/MathML"> J ( k , b ) = ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 J(k,b) = \sum_{i=1}^{m}(h(x^{(i)}) - y^{(i)})^2 </math>J(k,b)=∑i=1m(h(x(i))−y(i))2

上面的式子还等于 = <math xmlns="http://www.w3.org/1998/Math/MathML"> ∑ i = 1 m ( k x ( i ) + b − y ( i ) ) 2 \sum_{i=1}^{m}(kx^{(i)} + b - y^{(i)})^2 </math>∑i=1m(kx(i)+b−y(i))2 的极小值

损失函数是关于k、b的函数，对k、b分别求导设置成 0，得到2个方程

这是一个复杂的公式，省略常数实数

对 k 求导

= <math xmlns="http://www.w3.org/1998/Math/MathML"> ( k x ( i ) + b − y ( i ) ) 2 (kx^{(i)} + b - y^{(i)})^2 </math>(kx(i)+b−y(i))2

= <math xmlns="http://www.w3.org/1998/Math/MathML"> 2 ( k x ( i ) + b − y ( i ) ) ( k x ( i ) + b − y ( i ) ) ′ 2(kx^{(i)} + b - y^{(i)})(kx^{(i)} + b - y^{(i)})' </math>2(kx(i)+b−y(i))(kx(i)+b−y(i))′

= <math xmlns="http://www.w3.org/1998/Math/MathML"> 2 ( k x ( i ) + b − y ( i ) ) x ( i ) 2(kx^{(i)} + b - y^{(i)})x^{(i)} </math>2(kx(i)+b−y(i))x(i)

= <math xmlns="http://www.w3.org/1998/Math/MathML"> 2 k x ( i ) 2 + 2 b x ( i ) − 2 x ( i ) y ( i ) = 0 2kx^{(i)^{2}} + 2bx^{(i)} - 2x^{(i)}y^{(i)} = 0 </math>2kx(i)2+2bx(i)−2x(i)y(i)=0

对 b 求导

= <math xmlns="http://www.w3.org/1998/Math/MathML"> ( k x ( i ) + b − y ( i ) ) 2 (kx^{(i)} + b - y^{(i)})^2 </math>(kx(i)+b−y(i))2

= <math xmlns="http://www.w3.org/1998/Math/MathML"> 2 ( k x ( i ) + b − y ( i ) ) ⋅ 1 2(kx^{(i)} + b - y^{(i)}) · 1 </math>2(kx(i)+b−y(i))⋅1

= <math xmlns="http://www.w3.org/1998/Math/MathML"> 2 ( k x ( i ) + b − y ( i ) ) 2(kx^{(i)} + b - y^{(i)}) </math>2(kx(i)+b−y(i))

= <math xmlns="http://www.w3.org/1998/Math/MathML"> 2 k x ( i ) + 2 b − 2 y ( i ) = 0 2kx^{(i)} + 2b - 2y^{(i)} = 0 </math>2kx(i)+2b−2y(i)=0

完整答案

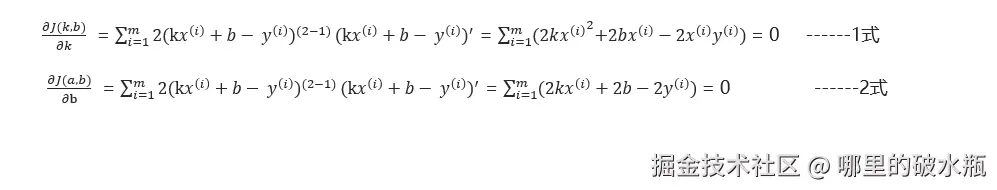
解析来继续变形，对上面的一式和二式

上面的答案完整的都有一个求和，因为样本数量是多个。

K 的求导结果变形

= <math xmlns="http://www.w3.org/1998/Math/MathML"> ∑ i = 1 m 2 k x ( i ) 2 + ∑ i = 1 m 2 b x ( i ) − ∑ i = 1 m 2 x ( i ) y ( i ) = 0 \sum_{i=1}^{m}2kx^{(i)^2} + \sum_{i=1}^{m}2bx^{(i)} - \sum_{i=1}^{m}2x^{(i)}y^{(i)} = 0 </math>∑i=1m2kx(i)2+∑i=1m2bx(i)−∑i=1m2x(i)y(i)=0

= 同时除以2

= <math xmlns="http://www.w3.org/1998/Math/MathML"> k ∑ i = 1 m x ( i ) 2 + ∑ i = 1 m b x ( i ) − ∑ i = 1 m x ( i ) y ( i ) = 0 k\sum_{i=1}^{m}x^{(i)^2} + \sum_{i=1}^{m}bx^{(i)} - \sum_{i=1}^{m}x^{(i)}y^{(i)} = 0 </math>k∑i=1mx(i)2+∑i=1mbx(i)−∑i=1mx(i)y(i)=0

B 的求导结果变形

= <math xmlns="http://www.w3.org/1998/Math/MathML"> ∑ i = 1 m 2 ( k x ( i ) + 2 b − 2 y ( i ) ) = 0 \sum_{i = 1}^{m}2(kx^{(i)} + 2b - 2y^{(i)}) = 0 </math>∑i=1m2(kx(i)+2b−2y(i))=0

= <math xmlns="http://www.w3.org/1998/Math/MathML"> k ∑ i = 0 m x ( i ) + ∑ ( i = 0 ) m b − ∑ ( i = 0 ) m y ( i ) = 0 k\sum_{i = 0}^{m}x^{(i)} + \sum_{(i = 0)}^{m}b - \sum_{(i = 0)}^{m}y^{(i)} = 0 </math>k∑i=0mx(i)+∑(i=0)mb−∑(i=0)my(i)=0

= <math xmlns="http://www.w3.org/1998/Math/MathML"> k ∑ i = 0 m x ( i ) + b m − ∑ ( i = 0 ) m y ( i ) = 0 k\sum_{i = 0}^{m}x^{(i)} + bm - \sum_{(i = 0)}^{m}y^{(i)} = 0 </math>k∑i=0mx(i)+bm−∑(i=0)my(i)=0

数据带入

已知 x 是身高，y 是体重

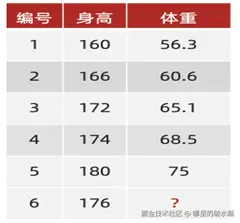
对 K 求

= <math xmlns="http://www.w3.org/1998/Math/MathML"> k ∗ ( 16 0 2 + 16 6 2 + 17 2 2 + 17 4 2 + 18 0 2 ) + b ∗ ( 160 + 166 + 172 + 174 + 180 ) -- ( 160 ∗ 56.3 + 166 ∗ 60.6 + 172 ∗ 65.1 + 174 ∗ 68.5 + 180 ∗ 75 ) = 0 k*(160^2+166^2+172^2+174^2+180^2)+b*(160+166+172+174+180)--(160*56.3+166*60.6+172*65.1+174*68.5+180*75)=0 </math>k∗(1602+1662+1722+1742+1802)+b∗(160+166+172+174+180)--(160∗56.3+166∗60.6+172∗65.1+174∗68.5+180∗75)=0

= <math xmlns="http://www.w3.org/1998/Math/MathML"> 145416 ∗ k + 852 ∗ b − 55683.8 = 0 145416*k + 852*b - 55683.8 = 0 </math>145416∗k+852∗b−55683.8=0

对 b 求

= <math xmlns="http://www.w3.org/1998/Math/MathML"> k ∗ ( 160 + 166 + 172 + 174 + 180 ) + b ∗ 5 − ( 56.3 + 60.6 + 65.1 + 68.5 + 75 ) = 0 k*(160+166+172+174+180)+b*5-(56.3+60.6+65.1+68.5+75)=0 </math>k∗(160+166+172+174+180)+b∗5−(56.3+60.6+65.1+68.5+75)=0

= <math xmlns="http://www.w3.org/1998/Math/MathML"> 852 ∗ k + 5 ∗ b − 325.5 = 0 852*k + 5*b - 325.5 = 0 </math>852∗k+5∗b−325.5=0