【C++】2.3 二叉搜索树的实现（附代码）

wregjru2025-12-24 8:39

二叉搜索树

左子树<=根，右子树>=根

根据需求不同，等于的元素可能会被去重也可能会被留下

这样查找一个数就可以只遍历一次，数大选哪个右走，小往左走

查找效率：ologn~on

改进：AVL树，红黑树，B树系列，查找效率：ologn

模拟实现（不多插入相同元素）

一．Key结构

1. 节点的定义

cpp 复制代码 
template<class K>
struct bsnode
{
    K _key;
    bsnode* _left;
    bsnode* _right;
    bsnode(const K& key)
        :_key(key)
        ,_left(nullptr)
        ,_right(nullptr)
    {}
};

2. 成员

cpp 复制代码 
typedef bsnode<K> node;
node* _root = nullptr;
复制代码 
这样，可以不用写构造函数

3. 二叉树的插入

cpp 复制代码 
bool insert(const K& key)
{
    if (_root == nullptr)
    {
        _root = new node(key);
        return 1;
    }
    node* cur = _root;
    node* par = nullptr;
    while (cur != nullptr)
    {
        if (cur->_key < key)
        {
            par = cur;
            cur = cur->_right;
        }
        else if (cur->_key > key)
        {
            par = cur;
            cur = cur->_left;
        }
        else
        {
            return 0;
        }
    }
    node* newnode = new node(key);
    if (par->_key < key)
    {
        par->_right = newnode;
    }
    else
    {
        par->_left = newnode;
    }
    return 1;
}

方案：定一个cur的指针，当根节点小于插入元素，向右走，大于则向左走

如果已经有这个数了，则返回false

如果cur为空，则构造一个节点，和cur最后一次经过的节点连接，返回true

那么，cur已经指向空了，怎么才能知道cur最后一次经过的节点？

在额外弄一个par指针尾随cur即可

4. 树排序

二叉搜索树的中序遍历（左->中->右）的特点：为从小到大的数组

因此，可以中序遍历得到有序数组，叫做树排序

cpp 复制代码 
void inorder()
{
    _inorder(_root);
}

void _inorder(node* root)
{
    if (root == nullptr)return;
    _inorder(root->_left);
    std::cout << root->_key << " ";
    _inorder(root->_right);
}

5. 查找

和插入同理，但是要找的值大于节点向右走，小于往左走

cpp 复制代码 
bool find(const K& _key)
{
    node* cur = _root;
    while (cur)
    {
        if (_key < cur->_key)
        {
            cur = cur->_left;
        }
        else if (_key > cur->_key)
        {
            cur = cur->_right;
        }
        else
        {
            return 1;
        }
    }
    return 0;
}

6. 删除（重要）

删除的集中情况（设删除节点的名称为M）

  1. M子节点左右均空：直接删除即可

  2. M子节点一个为空：M父节点指向M的一个子节点，再删除M

  3. M左右节点都为空：

    替换删除法：将M节点用下面的节点交换，再删除下面的数字节点

    那么和哪个节点交换既可以做到快速删除又可以做到保持左子树<=根，右子树>=根的性质呢

    和左子树的最右节点（最大节点）或右子树的最左节点（最小节点）

    （1）删除快速：由于两个情况都是最左或最右节点，因此一定满足删除方案1或2，因此删除简单

    （2）由于两个情况要么是小的最大，要么是大的最小，因此性质也是满足的

    下面用右边最左来演示

cpp 复制代码 
bool erase(const K& _key)
{
    node* par = nullptr;
    node* cur = _root;
    while (cur)
    {
        if (cur->_key < key)
        {
            par = cur;
            cur = cur->_right;
        }
        else if (cur->_key > key)
        {
            par = cur;
            cur = cur->_left;
        }
        else
        {
            if (cur->_left == nullptr)
            {
                if (cur == _root)
                {
                    _root = cur->_right;
                }
                else
                {
                    if (par->_left == cur)
                    {
                        par->_left = cur->_right;
                    }
                    else
                    {
                        par->_right = cur->_right;
                    }
                }
                delete cur;
            }
            else if (cur->_right == nullptr)
            {
                if (cur == _root)
                {
                    _root = cur->_left;
                }
                else
                {
                    if (par->_left == cur)
                    {
                        par->_left = cur->_left;
                    }
                    else
                    {
                        par->_right = cur->_left;
                    }
                }
                delete cur;
            }
            else
            {
                node* rp = cur;
                node* r = cur->_right;
                while (r->_left)
                {
                    rp = r;
                    r = r->_left;
                }
                cur->_key = r->_key;
                if (rp->_left == r)
                {
                    rp->_left = r->_right;
                }
                else
                {
                    rp->_right = r->_right;
                }
                delete r;
            }
            return 1;
        }
    }
    return 0;
}

代码逻辑

  1. 先找值为val的节点（找不到返回0），设找到的节点为M

  2. 节点M左为空：

    （1）节点M为根节点：直接将右节点设为根节点（有没有右节点都无所谓）

    （2）M不为根节点：

    A.M为左节点：M根节点连接M右节点，删M

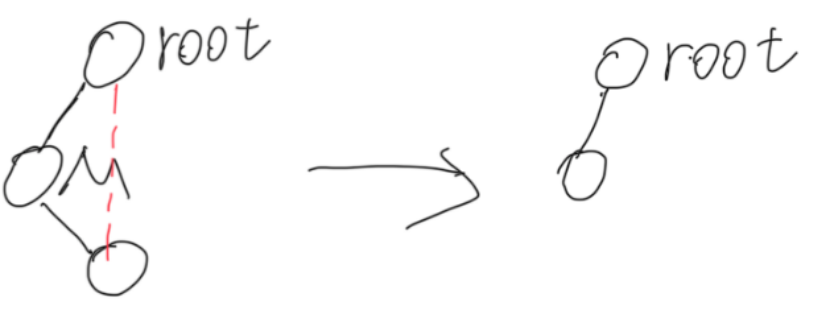
    B.M为右节点：M根节点连接M右节点，删M

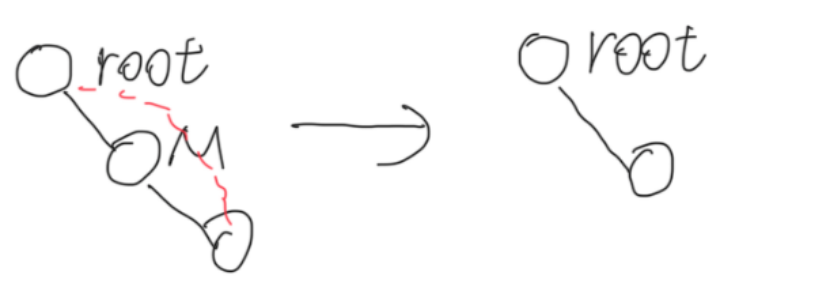
  3. 节点M右为空，同上：

    （1）节点M为根节点：直接将左节点设为根节点

    （2）M不为根节点：

    A.M为左节点：M根节点连接M左节点，删M

    B.M为右节点：M根节点连接M左节点，删M

  4. M左右都不为空（即else）

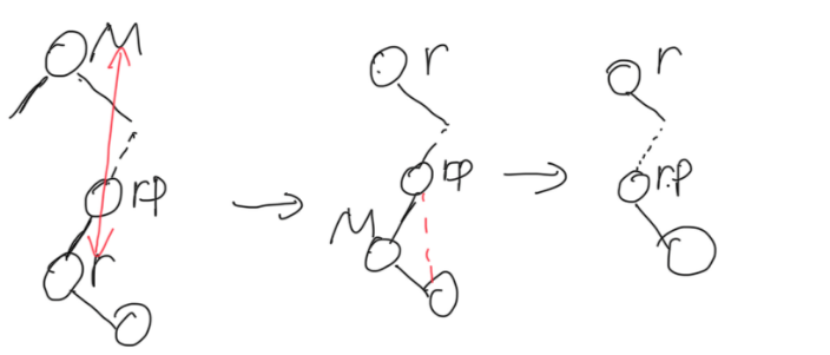
    先去寻找右子树的最左节点（设为r，r的父节点设为rp）

    由于r为最左节点，因此左边不会有子节点

    （1）正常情况：r为rp左节点

    交换r和M的值，再删r节点连rp和r子节点

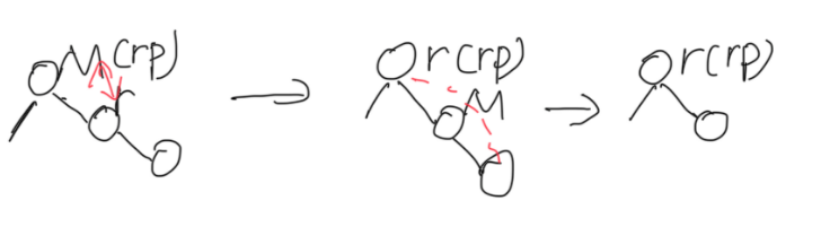
    （2）反常情况：M的子节点只有右节点

    此时M就是rp，r为rp右节点，和正常情况恰好相反

    交换r和M的值，再删r节点连rp和r子节点

二．Key-value结构

由于二叉树不一定每一个成员代表的都是1，因此用value记录数值

所有程序和key结构一样，只是模板，节点构造函数多了value而已

cpp 复制代码 
template<class K,class V>
struct bsnode
{
    K _key;
    V _val;
    bsnode* _left;
    bsnode* _right;
    bsnode(const K& key,const V& val)
        :_key(key)
        ,_val(val)
        ,_left(nullptr)
        ,_right(nullptr)
    {
    }
};

三．构造，析构函数

1. 前序遍历拷贝构造

先拷贝值，再拷贝子节点

由于拷贝构造无法递归，因此先写前序遍历再复用

递归函数

cpp 复制代码 
node* copy(node* root)
{
    if (root == nullptr)return nullptr;
    node* newroot = new node(root->_key, root->_val);
    newroot->_left = copy(root->_left);
    newroot->_right = copy(root->_right);
    return newroot;
}

拷贝构造

cpp 复制代码 
bstree(const bstree& t)
{
    _root = copy(t._root);
}

由于写了拷贝构造就不会生成默认构造，因此强制生成

cpp 复制代码 
bstree() = default;

2. 后序析构函数

先析构子节点，再析构自身

由于析构无法递归，因此先写前序遍历再复用

cpp 复制代码 
void destroy(node*root)
{
    if (root==nullptr)
    {
        return;
    }
    destroy(root->_left);
    destroy(root->_right);
    delete root;
    root = nullptr;
}

~bstree()
{
    destroy(_root);
    _root = nullptr;
}

3. 赋值重载

现代写法，直接交换，再销毁原来的

cpp 复制代码 
bstree&operator=(bstree t)
{
    std::swap(_root, t._root);
    return *this;
}

代码

cpp 复制代码 
#include<iostream>
#include<assert.h>


namespace key
{
	template<class K>
	struct bsnode
	{
		K _key;
		bsnode* _left;
		bsnode* _right;
		bsnode(const K&key)
			:_key(key )
			,_left(nullptr)
			,_right(nullptr)
		{ }
	};

	template<class K>
	class bstree
	{
	public:
		typedef bsnode<K> node;
		bool insert(const K& key)
		{
			if (_root == nullptr)
			{
				_root = new node(key);
				return 1;
			}
			node* cur = _root;
			node* par = nullptr;
			while (cur != nullptr)
			{
				if (cur->_key < key)
				{
					par = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					par = cur;
					cur = cur->_left;
				}
				else
				{
					return 0;
				}
			}
			node* newnode = new node(key);
			if (par->_key < key)
			{
				par->_right = newnode;
			}
			else
			{
				par->_left = newnode;
			}
			return 1;
		}
		void inorder()
		{
			_inorder(_root);
		}
		//bool find(const K& val)
		//{
		//	node* cur = _root;
		//}
		bool find(int _key)
		{
			node* cur = _root;
			while (cur)
			{
				if (_key < cur->_key)
				{
					cur = cur->_left;
				}
				else if (_key > cur->_key)
				{
					cur = cur->_right;
				}
				else
				{
					return 1;
				}
			}
			return 0;
		}
		bool erase(int key)
		{
			node* par = nullptr;
			node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					par = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					par = cur;
					cur = cur->_left;
				}
				else
				{
					if (cur->_left == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (par->_left == cur)
							{
								par->_left = cur->_right;
							}
							else
							{
								par->_right = cur->_right;
							}
						}
						delete cur;
					}
					else if (cur->_right == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_left;
						}
						else
						{
							if (par->_left == cur)
							{
								par->_left = cur->_left;
							}
							else
							{
								par->_right = cur->_left;
							}
						}
						delete cur;
					}
					else
					{
						node* rp = cur;
						node* r = cur->_right;
						while (r->_left)
						{
							rp = r;
							r = r->_left;
						}
						cur->_key = r->_key;
						if (rp->_left == r)
						{
							rp->_left = r->_right;
						}
						else
						{
							rp->_right = r->_right;
						}
						delete r;
					}
					return 1;
				}
			}
			return 0;
		}

	private:
		void _inorder(node* root)
		{
			if (root == nullptr)return;
			_inorder(root->_left);
			std::cout << root->_key << " ";
			_inorder(root->_right);
		}
		node* _root = nullptr;
	};
}


namespace key_value
{
	template<class K,class V>
	struct bsnode
	{
		K _key;
		V _val;
		bsnode* _left;
		bsnode* _right;
		bsnode(const K& key,const V& val)
			:_key(key)
			,_val(val)
			, _left(nullptr)
			, _right(nullptr)
		{
		}
	};

	template<class K,class V>
	class bstree
	{
	public:
		typedef bsnode<K,V> node;
		bstree(const bstree& t)
		{
			_root = copy(t._root);
		}
		bstree() = default;
		bstree&operator=(bstree t)
		{
			std::swap(_root, t._root);
			
			return *this;
		}
		bool insert(const K& key, const V& val)
		{
			if (_root == nullptr)
			{
				_root = new node(key,val);
				return 1;
			}
			node* cur = _root;
			node* par = nullptr;
			while (cur != nullptr)
			{
				if (cur->_key < key)
				{
					par = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					par = cur;
					cur = cur->_left;
				}
				else
				{
					return 0;
				}
			}
			node* newnode = new node(key,val);
			if (par->_key < key)
			{
				par->_right = newnode;
			}
			else
			{
				par->_left = newnode;
			}
			return 1;
		}
		void inorder()
		{
			_inorder(_root);
		}
		//bool find(const K& val)
		//{
		//	node* cur = _root;
		//}
		node* find(const K& _key)
		{
			node* cur = _root;
			while (cur)
			{
				if (_key < cur->_key)
				{
					cur = cur->_left;
				}
				else if (_key > cur->_key)
				{
					cur = cur->_right;
				}
				else
				{
					return cur;
				}
			}
			return nullptr;
		}
		bool erase(const K& key)
		{
			node* par = nullptr;
			node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					par = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					par = cur;
					cur = cur->_left;
				}
				else
				{
					if (cur->_left == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (par->_left == cur)
							{
								par->_left = cur->_right;
							}
							else
							{
								par->_right = cur->_right;
							}
						}
						delete cur;
					}
					else if (cur->_right == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_left;
						}
						else
						{
							if (par->_left == cur)
							{
								par->_left = cur->_left;
							}
							else
							{
								par->_right = cur->_left;
							}
						}
						delete cur;
					}
					else
					{
						node* rp = cur;
						node* r = cur->_right;
						while (r->_left)
						{
							rp = r;
							r = r->_left;
						}
						cur->_key = r->_key;
						cur->_val = r->_val;
						if (rp->_left == r)
						{
							rp->_left = r->_right;
						}
						else
						{
							rp->_right = r->_right;
						}
						delete r;
					}
					return 1;
				}
			}
			return 0;
		}
		~bstree()
		{
			destroy(_root);
			_root = nullptr;
		}

	private:
		node* copy(node* root)
		{
			if (root == nullptr)return nullptr;
			node* newroot = new node(root->_key, root->_val);
			newroot->_left = copy(root->_left);
			newroot->_right = copy(root->_right);
			return newroot;
		}
		void _inorder(node* root)
		{
			if (root == nullptr)return;
			_inorder(root->_left);
			std::cout << root->_key << ":" << root->_val << " ";
			_inorder(root->_right);
		}
		void destroy(node*root)
		{
			if (root==nullptr)
			{
				return;
			}
			destroy(root->_left);
			destroy(root->_right);
			delete root;
			root = nullptr;
		}
		node* _root = nullptr;
	};
}
相关推荐
Hao_Harrision2 小时前
50天50个小项目 (React19 + Tailwindcss V4) ✨ | StickyNavbar（粘性导航栏）
前端·typescript·react·tailwindcss·vite7
IT古董2 小时前
企业级官网全栈(React·Next.js·Tailwind·Axios·Headless UI·RHF·i18n)实战教程-前言
javascript·react.js·ui
LYFlied2 小时前
前端性能优化常见面试问题汇总
前端·面试·性能优化
柒.梧.2 小时前
Java核心面试题终极总结：从基础到进阶，覆盖高频考
java·开发语言·面试
不爱学习的老登2 小时前
基于CodeServer打造一个属于自己的 LaTeX Web 编辑器
前端·编辑器
黎雁·泠崖2 小时前
C 语言字符串入门：字符函数 + strlen 精讲（从使用到模拟实现）
c语言·开发语言
星环处相逢2 小时前
Docker资源限制全解析：CPU、内存、磁盘IO管控与实操指南
java·开发语言
white-persist2 小时前
【攻防世界】reverse | tt3441810 详细题解 WP
java·c语言·开发语言·数据结构·c++·算法·安全
四维碎片2 小时前
【Qt】为什么QList是数组
开发语言·qt
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）05解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题06Gemini3 生成的基于手势控制3D粒子圣诞树07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08CentOS的ISO镜像下载09Multisim使用教程详尽版--(2025最新版)10Labelme从安装到标注：零基础完整指南