一、传统特征波长选择的局限性
我们要处理的光谱数据(比如近红外 NIR),通常有成百上千个波长点(例如 1024 个点),但真正决定化学性质(比如糖度)的往往只有其中几个特定的波段,那么可能会遇到以下两种情况:
- 如果数据很干净(信号强): 也许只需要 5% 的关键波长就够了,强制留 20% 会引入 15% 的噪音(过拟合)。
- 如果数据很嘈杂(信号弱): 也许你需要保留 40% 的波长才能凑齐足够的信息,强制只留 20% 就会丢失关键信息(欠拟合)。
- 结果: 你很难找到那个完美的平衡点,往往需要反复试错,非常耗时。
上述两种情况就体现了传统方法的以下两点问题:
1.稀疏度固定或难于调整:稀疏度指的是模型保留多少个特征点(波长)。传统方法通常需要预先设置一个惩罚参数,比如lasso中的λ值,来决定保留多少点。这个参数不容易直观调整,导致模型有时保留太多无关点(造成过拟合,模型对新数据预测差),有时又保留太少(造成欠拟合,丢失重要信息)。
2.不支持灵活的结构化稀疏:光谱数据有自然结构,比如连续的波长点形成一个"谱带",这些点对应特定的化学特征(如糖的C-H振动),这也就是光谱数据处理与传统特征工程不同的点,我们往往选择连续的波段截取,而不是提取离散的分离点。传统PLS可以做一些稀疏,但对组稀疏支持不好。组稀疏意思是将相邻点作为一个组来处理,而不是单独点。这样选出的特征往往是零散的单个点,而不是完整的谱带,这让模型的解释性差,无法清楚说明哪些化学区域重要。
二、Dual-sPLS方法的引入
2.1 范数的概念
假设你有一条光谱数据,在5个波长下测量,得到数值是 [2, -3, 5, -1, 4]。
L1范数的计算: 把所有数值的绝对值加起来: |2| + |-3| + |5| + |-1| + |4| = 2 + 3 + 5 + 1 + 4 = 15
L2范数的计算: 先把每个数值平方,加起来,再开方: √(2² + (-3)² + 5² + (-1)² + 4²) = √(4 + 9 + 25 + 1 + 16) = √55 ≈ 7.42
L∞范数的计算: 找出绝对值最大的那个数: 在 [2, -3, 5, -1, 4] 中,绝对值最大的是5,所以L∞范数 = 5
就这么简单,范数就是把一堆数字按照不同规则"浓缩"成一个数值。在光谱分析中,我们不是直接对光谱数据算范数,而是对权重向量算范数。比如算法给5个波长分配的权重是 [0.8, 0, 0.3, 0, 0.5],它的L1范数就是 0.8+0+0.3+0+0.5=1.6。通过限制这个1.6不能太大(比如要求≤1.0),算法就会被迫把一些权重压到零,从而实现波长筛选。
2.2 Dual-sPLS的原理
Dual-sPLS 的数学形式(对偶范数)天然支持 Group Lasso(组稀疏)。
- 结构化选择: 你可以告诉算法:"请把相邻的波长看作一组"。算法在筛选时,要么把这整个波段都留下,要么整个都扔掉。这极大地提高了模型的 解释性。选出来的不再是零散的点,而是完整的吸收峰,这与化学原理(分子振动能级)是吻合的。
为什么L1范数能确保稀疏?
这是L1范数的几何特性决定的:
- 假设两个波长的权重是 [w₁, w₂]
- L1约束 :|w₁| + |w₂| ≤ 1,在平面上画出来是一个菱形(有4个尖角)
- L2约束 :√(w₁² + w₂²) ≤ 1,画出来是一个圆形(光滑无尖角)
当优化算法寻找"协方差最大"的权重时,相当于在这个约束区域内找最优点。关键来了:
- L1的菱形有尖角,尖角正好在坐标轴上(比如点(1,0)或(0,1)),意味着某些权重恰好=0
- 优化过程很容易"撞到"这些尖角,自然产生大量零权重(稀疏)
- 而L2的圆形光滑,优化结果通常是(0.7, 0.7)这种所有权重都非零的情况
如果有500个波长,L1约束会逼迫算法把权重分配成 [0.8, 0, 0, 0.3, 0, ..., 0.5, 0] 这种只有15个非零的形式(自动选出15个关键波长,其他485个全部剔除);而L2约束可能给出500个都非零的密集权重,无法实现特征选择。
但这样求解很难: 这就像在"最大化协方差"和"控制L1范数"两个目标之间走钢丝,数学上很难直接求解,因为L1范数产生的"尖角"让优化算法容易卡住(导数在尖角处不存在)。传统方法需要反复迭代试探,计算慢且容易陷入局部最优(找到的不是真正最好的那15个波长)。
对偶范数的妙用: Dual-sPLS使用了一个数学技巧:不直接限制权重的L1范数,而是转到"对偶空间"求解。对偶范数是这样定义的------L1范数的对偶是L∞范数(回忆:L∞就是取绝对值最大的那个数)。通过数学变换,原问题变成:在L∞范数≤1的约束下,找一个向量最大化另一个目标。
为什么这样更简单?
- 原问题:要同时考虑"协方差大不大"和"L1范数有没有超标",两件事纠缠在一起,且L1的尖角让求导困难
- 对偶问题 :先不管约束,算出一个"理想向量";然后把这个向量投影到L∞范数球上(就像把一个点拉回到允许范围内),投影操作可以用简单公式完成
具体怎么操作:
- 用SVD(奇异值分解)快速算出"不考虑稀疏约束时的最优方向"(可能500个波长都有权重)
- 用软阈值算子 把这个方向"修剪"成稀疏的------软阈值就是:如果某个权重的绝对值小于阈值λ,直接砍成0;否则往0的方向缩λ个单位(比如2.5变成2.5-λ,-1.8变成-1.8+λ)。这个操作正好对应投影到对偶范数球,自动把不重要的485个波长权重清零,只保留15个关键波长
本质优势: 原来是"边优化边约束"(很难,因为L1的尖角),现在是"先优化,后投影"(两步都很简单)。软阈值算子天然地把小权重清零,保留重要波长,实现稀疏性。就像你本来要在有尖刺的山坡上找最高点且不能离营地太远,很难走;现在改成先爬到最高点,再用一把"修枝剪"(软阈值)把不重要的485根枝条剪掉、只留15根粗壮的,每一步都清晰可执行。这避免了算法在复杂地形中迷路(局部最优),保证能稳定收敛到真正重要的波长组合,最终得到既准确又简洁、抗噪声能力强的模型。
完整实现代码示例如下:
python
import os
import matplotlib
matplotlib.use('TkAgg')
import csv
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error, r2_score
from scipy.signal import savgol_filter
import seaborn as sns
from BaselineRemoval import BaselineRemoval
# 设置绘图样式
sns.set(context='notebook', style='darkgrid', palette='deep', font='sans-serif', font_scale=1, color_codes=False)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# ==========================================
# 实现 Dual-sPLS 类
# ==========================================
class DualSPLS:
"""
基于 Dual-sPLS 原理的稀疏偏最小二乘回归。
核心逻辑:
1. SVD 计算协方差最大化方向 (unconstrained direction)
2. Soft-Thresholding 算子进行稀疏化投影 (L1/L_inf constraint)
3. Deflation (剥离已解释的信息)
"""
def __init__(self, n_components=2, sparsity_alpha=0.0):
"""
:param n_components: 潜变量(Latent Variables)个数
:param sparsity_alpha: 稀疏阈值 (lambda)。
0 表示不稀疏(退化为普通PLS),值越大稀疏度越高。
建议范围通常在 [0, 1) 之间,或者根据数据量级调整。
"""
self.n_components = n_components
self.alpha = sparsity_alpha
self.coef_ = None
self.x_mean_ = None
self.y_mean_ = None
self.x_weights_ = None # W
self.x_loadings_ = None # P
self.y_loadings_ = None # Q
def _soft_thresholding(self, x, alpha):
"""
软阈值算子 (Soft Thresholding Operator)
对应文中:如果绝对值小于阈值,直接砍成0;否则往0的方向缩减。
"""
if alpha <= 0:
return x
# sign(x) * max(|x| - alpha, 0)
return np.sign(x) * np.maximum(np.abs(x) - alpha, 0)
def fit(self, X, Y):
# 1. 数据中心化
self.x_mean_ = np.mean(X, axis=0)
self.y_mean_ = np.mean(Y, axis=0)
X_c = X - self.x_mean_
Y_c = Y - self.y_mean_
# 确保 Y 是二维的 (n_samples, 1)
if Y_c.ndim == 1:
Y_c = Y_c.reshape(-1, 1)
n_samples, n_features = X_c.shape
n_targets = Y_c.shape[1]
# 存储列表
W_list = [] # X weights
P_list = [] # X loadings
Q_list = [] # Y loadings
# 迭代提取成分 (Deflation Loop)
for k in range(self.n_components):
# --- Step 1: 计算协方差矩阵 M = X'Y ---
M = np.dot(X_c.T, Y_c)
# --- Step 2: SVD 求解最优非约束方向 ---
# 只需第一奇异向量,它指向协方差最大的方向
try:
# 某些情况下 svd 可能不收敛,使用 try-except
U_svd, S_svd, Vt_svd = np.linalg.svd(M, full_matrices=False)
w = U_svd[:, 0] # 获取左奇异向量作为权重初始值
except np.linalg.LinAlgError:
print("SVD did not converge, breaking loop.")
break
# --- Step 3: Dual-sPLS 核心 - 应用软阈值 (稀疏化) ---
# 这里对应将 "理想向量" 投影到 L_inf 球对应的对偶空间
w = self._soft_thresholding(w, self.alpha)
# --- Step 4: 归一化 (L2 Norm Constraint) ---
norm_w = np.linalg.norm(w)
if norm_w < 1e-10:
print(f"Warning: Component {k + 1} is empty (sparsity_alpha too high). Stopping.")
break
w = w / norm_w
# --- Step 5: 计算得分 (Scores) 和 载荷 (Loadings) ---
# t = Xw
t = np.dot(X_c, w).reshape(-1, 1)
# p = (X't) / (t't)
t_sq = np.dot(t.T, t)
if t_sq < 1e-10:
break
p = np.dot(X_c.T, t) / t_sq
q = np.dot(Y_c.T, t) / t_sq # 对于单目标回归,q 是标量
# --- Step 6: 剥离信息 (Deflation) ---
# X_new = X - t p'
# Y_new = Y - t q'
X_c = X_c - np.dot(t, p.T)
Y_c = Y_c - np.dot(t, q.T)
# 存储结果
W_list.append(w)
P_list.append(p.flatten())
Q_list.append(q.flatten())
# 转换为数组
self.x_weights_ = np.array(W_list).T # (n_features, n_components)
self.x_loadings_ = np.array(P_list).T # (n_features, n_components)
self.y_loadings_ = np.array(Q_list).T # (n_targets, n_components)
# --- Step 7: 计算最终回归系数 Beta ---
# standard PLS formula: Beta = W (P'W)^-1 Q'
# 注意:在稀疏情况下,P'W 可能会秩亏,使用 pinv (伪逆) 更加稳健
W = self.x_weights_
P = self.x_loadings_
Q = self.y_loadings_
try:
inner = np.dot(P.T, W)
inner_inv = np.linalg.pinv(inner)
self.coef_ = np.dot(np.dot(W, inner_inv), Q.T)
except Exception as e:
print(f"Error calculating coefficients: {e}")
self.coef_ = np.zeros((n_features, n_targets))
return self
def predict(self, X):
if self.coef_ is None:
raise ValueError("Model not fitted yet.")
X_c = X - self.x_mean_
return np.dot(X_c, self.coef_) + self.y_mean_
# ==========================================
# 数据预处理函数
# ==========================================
def preprocess_spectrum(spectrum_data, sg_w, sg_n, sg_d, lambda_, porder, norm_wavenumber, start_idx, end_idx):
# ...
# 读取数据函数 (保持不变)
def read_data(file_path, sg_w, sg_n, sg_d, lambda_, porder, start_idx, end_idx, norm_wavenumber):
X = []
Y = []
if not os.path.exists(file_path):
print(f"Warning: File not found: {file_path}")
return np.array([]), np.array([])
with open(file_path, mode='r', newline='', encoding='ISO-8859-1') as file:
reader = csv.reader(file)
try:
header = next(reader)
except StopIteration:
return np.array([]), np.array([])
previous_od_value = None
current_spectra = []
for row in reader:
if not row: continue # skip empty lines
try:
spectrum_data = [float(val) for val in row[3:3 + 1024]]
od_value = float(row[1])
except (ValueError, IndexError):
continue
spectrum_segment = spectrum_data[start_idx:end_idx]
preprocessed_spectrum = preprocess_spectrum(
spectrum_segment, sg_w, sg_n, sg_d, lambda_, porder, norm_wavenumber, start_idx, end_idx)
if previous_od_value is None or od_value != previous_od_value:
if current_spectra:
mean_spectrum = np.mean(current_spectra, axis=0)
X.append(mean_spectrum)
Y.append(previous_od_value)
current_spectra = [preprocessed_spectrum]
else:
current_spectra.append(preprocessed_spectrum)
previous_od_value = od_value
if current_spectra:
mean_spectrum = np.mean(current_spectra, axis=0)
X.append(mean_spectrum)
Y.append(previous_od_value)
return np.array(X), np.array(Y)
# 训练集和测试集路径
train_file_paths = [
r"D:\pythonProject\KangMa\Data\LabeledData\LabeledData0807.csv",
r"D:\pythonProject\KangMa\Data\LabeledData\LabeledData0813.csv",
r"D:\pythonProject\KangMa\Data\LabeledData\LabeledData0907.csv",
r"D:\pythonProject\KangMa\Data\LabeledData\LabeledData0920.csv",
r"D:\pythonProject\KangMa\Data\LabeledData\LabeledData1012.csv"
]
test_file_paths = [
r"D:\pythonProject\KangMa\Data\LabeledData\LabeledData0820.csv",
r"D:\pythonProject\KangMa\Data\LabeledData\LabeledData0828.csv",
]
def main():
# 参数设置
best_params = {
'sg_w': 47,
'sg_n': 14,
'sg_d': 1,
'lambda_': 76.19968486314983,
'porder': 42,
'start_idx': 169,
'end_idx': 363,
'n_components': 9,
'norm_wavenumber': 1645.412436,
# --- Dual-sPLS 特有参数 ---
# sparsity_alpha (lambda): 软阈值参数。
# 针对归一化后的光谱数据(数值通常较小),这个值需要仔细调整。
# 如果设得太大,所有系数都会变成0;如果太小,就接近普通PLS。
# 建议尝试值:0.05, 0.1, 0.2 等
'sparsity_alpha': 0.08
}
print("正在读取并处理数据...")
# 读取训练数据
X_train, Y_train = np.empty((0, best_params['end_idx'] - best_params['start_idx'])), np.empty((0,))
for fpath in train_file_paths:
X, Y = read_data(
fpath,
best_params['sg_w'], best_params['sg_n'], best_params['sg_d'],
best_params['lambda_'], best_params['porder'],
best_params['start_idx'], best_params['end_idx'],
best_params['norm_wavenumber']
)
if X.size > 0:
X_train = np.vstack([X_train, X]) if X_train.size else X
Y_train = np.concatenate([Y_train, Y]) if Y_train.size else Y
# 读取测试数据
X_test, Y_test = np.empty((0, best_params['end_idx'] - best_params['start_idx'])), np.empty((0,))
for fpath in test_file_paths:
X, Y = read_data(
fpath,
best_params['sg_w'], best_params['sg_n'], best_params['sg_d'],
best_params['lambda_'], best_params['porder'],
best_params['start_idx'], best_params['end_idx'],
best_params['norm_wavenumber']
)
if X.size > 0:
X_test = np.vstack([X_test, X]) if X_test.size else X
Y_test = np.concatenate([Y_test, Y]) if Y_test.size else Y
if X_train.shape[0] == 0:
print("错误:没有加载到训练数据,请检查路径。")
return
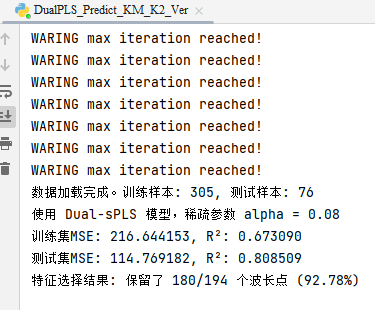
print(f"数据加载完成。训练样本: {X_train.shape[0]}, 测试样本: {X_test.shape[0]}")
print(f"使用 Dual-sPLS 模型,稀疏参数 alpha = {best_params['sparsity_alpha']}")
# --- 使用 Dual-sPLS 模型 ---
model = DualSPLS(
n_components=best_params['n_components'],
sparsity_alpha=best_params['sparsity_alpha']
)
model.fit(X_train, Y_train)
# 预测
# 注意:DualSPLS的predict返回的是(n, 1)数组,需要flatten以便和Y (n,) 对应
Y_pred_train = model.predict(X_train).flatten()
Y_pred_test = model.predict(X_test).flatten()
# 计算误差指标
mse_train = mean_squared_error(Y_train, Y_pred_train)
r2_train = r2_score(Y_train, Y_pred_train)
mse_test = mean_squared_error(Y_test, Y_pred_test)
r2_test = r2_score(Y_test, Y_pred_test)
print(f"训练集MSE: {mse_train:.6f}, R²: {r2_train:.6f}")
print(f"测试集MSE: {mse_test:.6f}, R²: {r2_test:.6f}")
# 计算非零系数数量(特征选择情况)
non_zero_features = np.sum(np.abs(model.coef_) > 1e-10)
total_features = model.coef_.shape[0]
print(
f"特征选择结果: 保留了 {non_zero_features}/{total_features} 个波长点 ({(non_zero_features / total_features) * 100:.2f}%)")
# 绘图
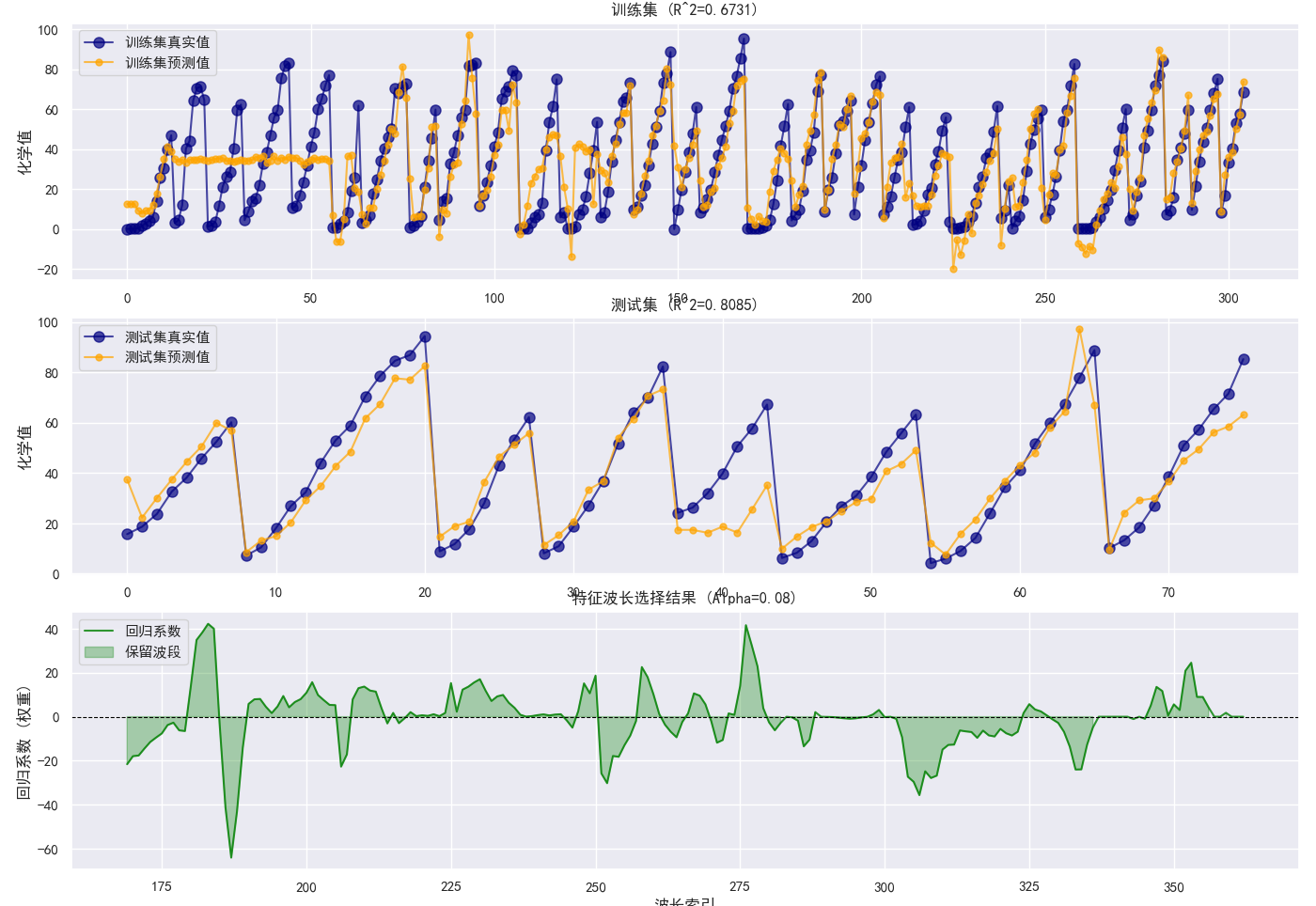
plt.figure(figsize=(14, 16))
# 1. 训练集预测图
plt.subplot(3, 1, 1)
indices_train = np.arange(len(Y_train))
plt.plot(indices_train, Y_train, 'o-', label='训练集真实值', color='navy', alpha=0.7, markersize=8)
plt.plot(indices_train, Y_pred_train, 'o-', label='训练集预测值', color='orange', alpha=0.7, markersize=5)
plt.ylabel('化学值')
plt.legend()
plt.title(f'训练集 (R^2={r2_train:.4f})')
plt.grid(True)
# 2. 测试集预测图
plt.subplot(3, 1, 2)
indices_test = np.arange(len(Y_test))
plt.plot(indices_test, Y_test, 'o-', label='测试集真实值', color='navy', alpha=0.7, markersize=8)
plt.plot(indices_test, Y_pred_test, 'o-', label='测试集预测值', color='orange', alpha=0.7, markersize=5)
plt.ylabel('化学值')
plt.legend()
plt.title(f'测试集 (R^2={r2_test:.4f})')
plt.grid(True)
# 3. 波长系数图 (展示稀疏性)
plt.subplot(3, 1, 3)
coefficients = model.coef_.flatten()
wavelength_indices = np.arange(len(coefficients)) + best_params['start_idx']
# 绘制所有系数
plt.plot(wavelength_indices, coefficients, label='回归系数', color='green', alpha=0.8)
# 标出为0的区域 (被剔除的波长)
plt.fill_between(wavelength_indices, 0, coefficients, where=(np.abs(coefficients) > 1e-10),
color='green', alpha=0.3, label='保留波段')
plt.axhline(0, color='black', linewidth=0.8, linestyle='--')
plt.xlabel('波长索引')
plt.ylabel('回归系数 (权重)')
plt.title(f'特征波长选择结果 (Alpha={best_params["sparsity_alpha"]})')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
if __name__ == "__main__":
main()运行结果: