Tetuan的电力消耗数据进行时间序列预测

数据清洗

处理缺失值

填充均值

在获取的原始数据中，部分时间段的数据存在缺失值，对于缺失值，采取数据填充的办法，填充的数据为样本平均值，为补上的平均值，其数据是相同观察天的平均值。
填充空

对于数值型数据，在pandas使用浮点值NaN，使用NaN作为标识容易被检测。
插值

运用线性插值，三次样条插值等方法将插值不全。

具体填补缺失值要考虑数据的形态，实际的应用要求，本报告中缺失值填充的为样本的均值。

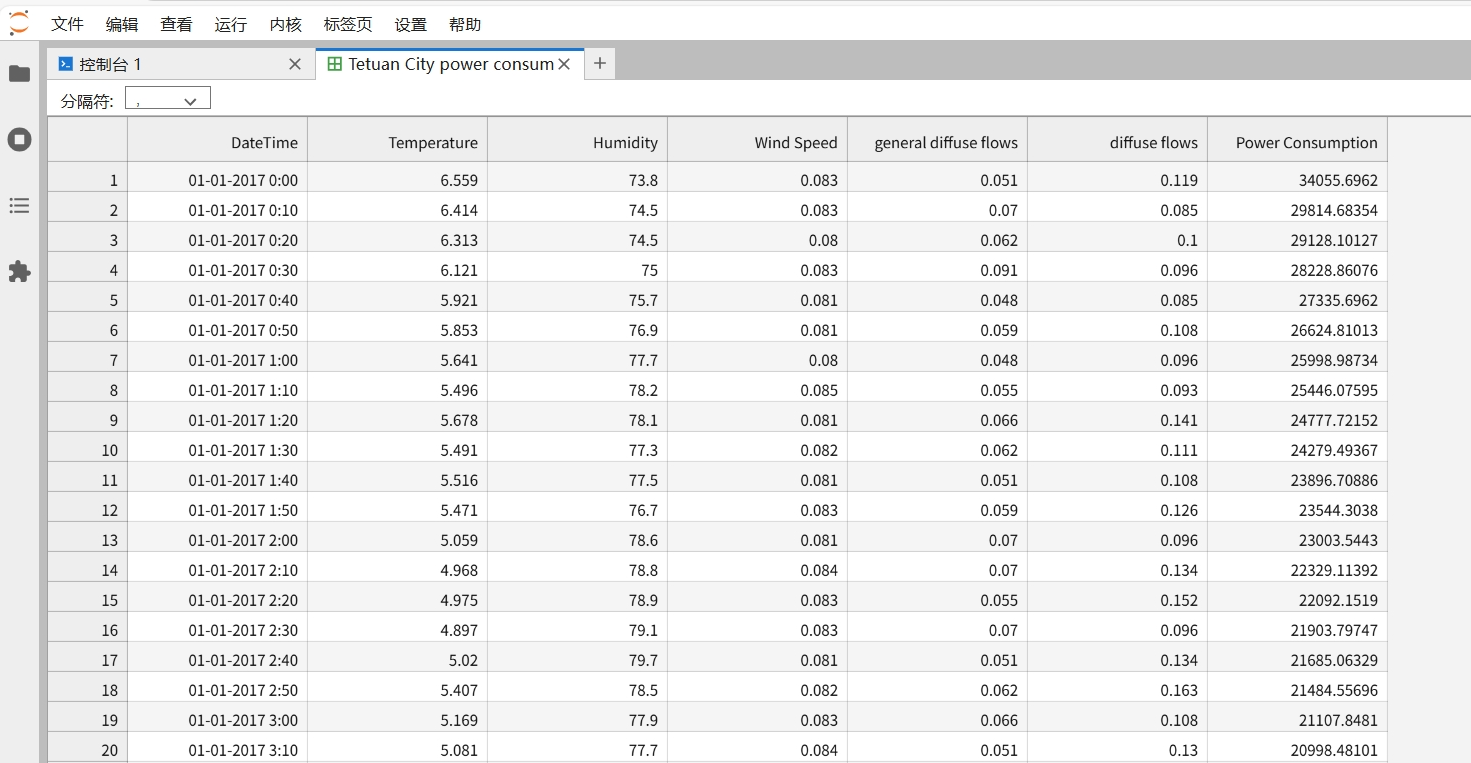
http://localhost:8888/lab/tree/Tetuan City power consumption.csv

LSTM预测

#导入核心库：数值计算、LSTM模型、数据处理、可视化、数据归一化
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM
from tensorflow.keras.layers import Dense, Dropout
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.preprocessing import MinMaxScaler
import seaborn as sns

#读取电力消耗数据集
df=pd.read_csv("Tetuan City power consumption.csv",parse_dates=["DateTime"],index_col=[0])
df.shape #查看数据维度

df.head() #预览前5行数据，确保数据正常

#划分训练/测试集（非传统按时间先后顺序）
df_for_training=df[601:3000]
df_for_testing=df[1:600]
print(df_for_training.shape)
print(df_for_testing.shape)

#数据归一化；将特征缩放到0-1之间（LSTM对数据敏感可视化是必要步骤）
scaler = MinMaxScaler(feature_range=(0,1))
df_for_training_scaled = scaler.fit_transform(df_for_training)
df_for_testing_scaled=scaler.transform(df_for_testing)
df_for_training_scaled.shape


df_for_testing_scaled.shape


# 构建时间序列样本；将序列数据转换为"输入序列+标签"的格式	
# n_past:用前n_past个时间步的特征预测当前时间步的特征值
def createXY(dataset,n_past):
    dataX = [] # 输入：前n_past个时间步的所有特征
    dataY = [] # 输出：当前时间步的第6列（电力消耗）
    for i in range(n_past, len(dataset)):
    				# 输入维度：（n_past, 特征数）
            dataX.append(dataset[i - n_past:i, 0:dataset.shape[1]])
            # 目标：第六列
            dataY.append(dataset[i,5])
    return np.array(dataX),np.array(dataY)        

# 生成训练/测试样本：用前10个时间步预测当前值
trainX,trainY=createXY(df_for_training_scaled,10)
testX,testY=createXY(df_for_testing_scaled,10)

# 导入网格搜索工具：用于自动调优模型超参数
from scikeras.wrappers import KerasRegressor
from sklearn.model_selection import GridSearchCV

# 定义lstm模型构建函数（网络搜索的模型基础）
def build_model():
    grid_model = Sequential()
    # 第一层LSTM：50个神经元，返回序列（因为后序还有LSTM层），输入维度：（10， 6）（10个时间步，6个特征）
    grid_model.add(LSTM(50,return_sequences=True,input_shape=(10,6)))
    # 第二层LSTM：50个神经元，不返回序列（后序接全连接层）
    grid_model.add(LSTM(50))
    # 随机丢弃20%的神经元，防止过拟合
    grid_model.add(Dropout(0.2))
    # 输出层：1个神经元（回归任务，预测连续值）
    grid_model.add(Dense(1))
		# 编译模型：损失函数MSE（回归任务），优化器由参数指定
    grid_model.compile(loss = 'mse',optimizer = 'sgd')
    return grid_model

# 初始化网格搜索：estimator为包装后的模型，param_grid为超参数空间，cv=2（2折交叉验证）
grid_model = KerasRegressor(build_fn=build_model,verbose=1)
# 定义网格搜索的超参数空间
parameters = {'batch_size' : [12], # 批次大小
              'epochs' : [10], # 训练轮数
              'optimizer' : ['adam','Adadelta'] } # 优化器
# 初始化网格搜索：estimator为包装后的模型，param_grid为超参数空间，cv=2（2折交叉验证）
grid_search  = GridSearchCV(estimator = grid_model,
                            param_grid = parameters,
                            cv = 2) #2-10


# 记录训练时间：评估网格搜索耗时
import time
t1 = time.perf_counter()
 # 执行网格搜索，训练并选择最优模型
grid_search = grid_search.fit(trainX,trainY) 
t2 = time.perf_counter()
total_time = (t2-t1)*1000 # 转换为毫秒

# 输出网格搜索总耗时
print(total_time)

# 搜索网格搜索后的最优模型
my_model=grid_search.best_estimator_
my_model # 打印最优模型的参数

# 用最优的模型测试测试集
prediction=my_model.predict(testX)	
print("\nPrediction Shape-",prediction.shape) # 输出预测结果维度

# 逆归一化准备：预测值仅为6列，需扩展为6列
prediction_copies_array = np.repeat(prediction,6, axis=-1)  # 重复6次，维度：(n,6)

prediction_copies_array.shape

# 逆归一化：恢复原始数值尺度（仅关注第6列，即电力消耗）
pred=scaler.inverse_transform(np.reshape(prediction_copies_array,(len(prediction),6)))
pred = pred[:,5]  # 提取第6列（预测的电力消耗）

# 测试集真实值逆归一化：同样扩展为6列后逆缩放，再提取第6列
original_copies_array = np.repeat(testY,6, axis=-1)
original_copies_array.shape
original=scaler.inverse_transform(np.reshape(original_copies_array,(len(testY),6)))[:,5]

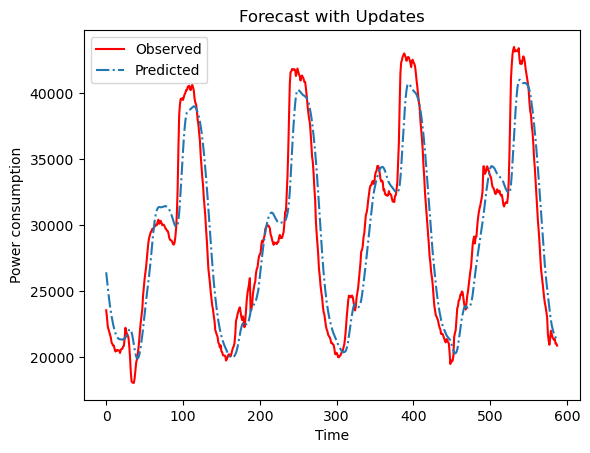
# 可视化1：预测值vs真实值（测试集范围内）
plt.plot(original, color = 'red', label = 'Observed')
plt.plot(pred, '-.', label = 'Predicted')
plt.title('Forecast with Updates')
plt.xlabel('Time')
plt.ylabel('Power consumption')
plt.legend()
plt.show()

ori = np.array(df[590:3000])[:,5]  # 原始数据第590-2999行的电力消耗
x_ori = np.linspace(1,2410,2410)
x_pred = np.linspace(2410,3000,588)
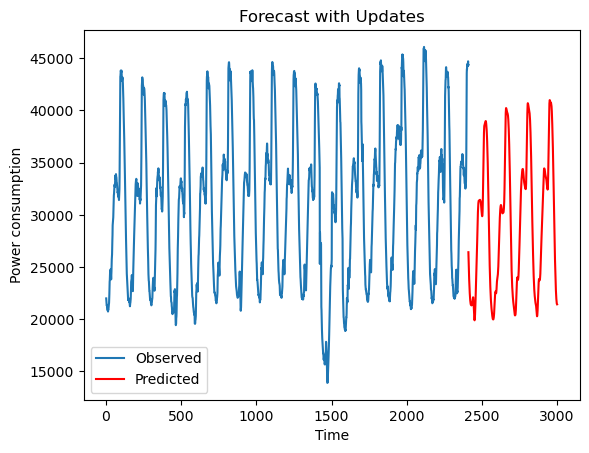
plt.plot(x_ori,ori,label = 'Observed')
plt.plot(x_pred,pred,color = 'red',label = 'Predicted')
plt.title('Forecast with Updates')
plt.xlabel('Time')
plt.ylabel('Power consumption')
plt.legend()
plt.show()

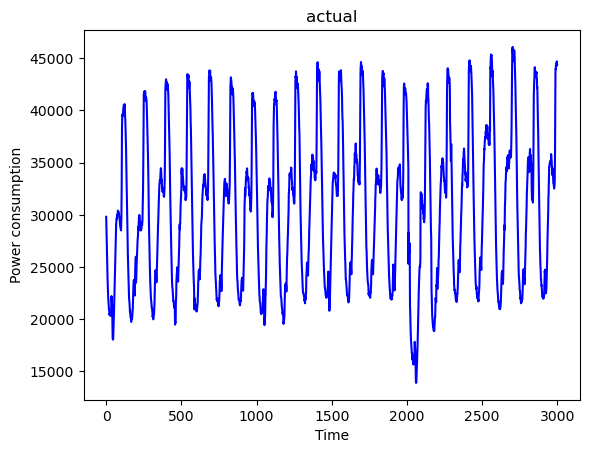
# 可视化3：完整原始数据（1-2999行）的电力消耗趋势
full_ori = np.array(df[1:3000])[:,5]
plt.plot(full_ori,color='blue')
plt.title('actual')
plt.xlabel('Time')
plt.ylabel('Power consumption')
plt.show()

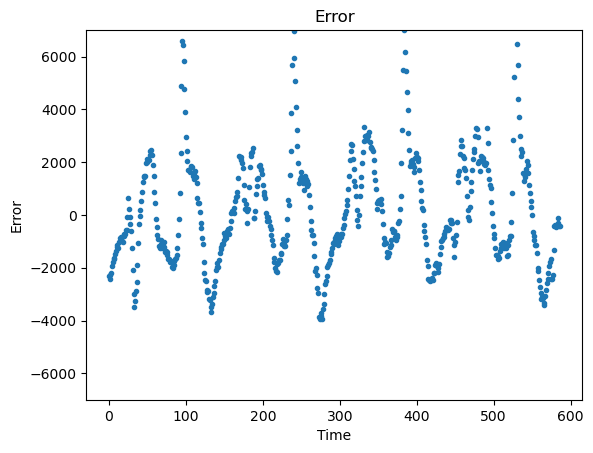
# 可视化4：预测误差（真实值-预测值）
error = original[:-1]-pred[1:] # 对齐维度后计算误差
plt.plot(error,'.')
plt.ylim([-7000,7000]) # 限制y轴范围，便于观察
plt.title('Error')
plt.xlabel('Time')
plt.ylabel('Error')
plt.show()

# 计算均方根误差（RMSE）：评估预测精度（值越小，预测越准）
rootMeanSquaredError = np.power(np.sum(np.power(error,2))/len(error),0.5)
print(rootMeanSquaredError)

预测价值

基础调度支撑

模型预测结果与电力消耗的周期性波动高度匹配，可直接支撑电网 "基础负荷调度"------ 业务部门能依据预测的周期趋势，提前 1-3 天规划常规发电资源（如火力机组基础出力、水电资源分配），减少日常调度的盲目性，降低基础运营成本。
无系统性偏差

预测结果误差为出现定向偏移，避免了因长期偏差导致的 "发电资源过度储备"（增加成本）或 "供电能力不足"（引发用户投诉），保障了运营效率与用户体验的平衡。

业务风险点

峰值供电缺口风险

模型对电力消耗 "峰值 / 谷值" 的预测误差较大，若峰值时段预测偏低，会导致供电能力不足、局部跳闸；若谷值时段预测偏高，会造成发电资源浪费，直接影响供电可靠性与运营经济性。
精细化业务受限

因未纳入 "小时级负荷特征"，模型无法精准捕捉 "日内负荷波动"（如早高峰、晚高峰的具体时段），无法支撑 "分时电价调整""峰谷时段错峰调度" 等精细化业务动作，制约了需求侧管理的效率。

合理化建议

电网调度采用分级响应、备用缓冲机制

以模型的 "周期性趋势预测" 为基础调度依据，同时针对 ±4000 的误差范围，配置15%-20% 的峰值备用资源池（如备用发电机组、储能设备）------ 当预测峰值负荷时，提前启动部分备用资源，覆盖误差缺口，避免供电中断。
特殊场景单独适配

针对历史数据中的 "极端负荷时段"（如节假日、极端高温 / 低温），梳理业务标签（如 "暴雨天"），与模型结果结合形成 "特殊场景调度规则"，提前 24 小时调整资源配置。
建立数据协同机制

在现有数据基础上，接入用户类型占比（居民 / 工业 / 商业）、节假日安排、本地重大活动计划等业务数据，提升模型对特殊场景的预测精度，减少极端误差。将模型预测结果接入电网调度系统，实时同步 "预测负荷" 与 "实际负荷" 数据，建立 "每日预测精度复盘机制"------ 若当日误差超过 ±2000，次日调整调度策略（如增加备用资源比例)。
从需求侧降低用电负荷波动

基于模型预测的 "波动趋势"，在误差较高的时段试点动态电价（如预测峰值前 2 小时提高电价，谷值时段降低电价），通过价格杠杆引导用户错峰用电，间接降低负荷波动的不确定性。在预测峰值时段前，通过短信、APP 推送 "错峰用电建议"（如工业用户避开 18:00-20:00 的居民用电高峰），平抑极端负荷，减少模型误差对业务的影响。

通过，可将模型的 "趋势预测价值" 最大化，同时规避预测误差带来的业务风险，实现电力供应的 "可靠性与经济性" 平衡。