矩阵,看似是由数字组成的冰冷表格,实则是描述空间变换的 "魔法咒语"。从手机拍照的裁剪旋转,到游戏中 3D 角色的动作舒展,再到人工智能的图像识别,背后都藏着矩阵操控空间的奥秘。接下来,我们将从直观感知到数学本质,一步步揭开这场 "空间转换魔术" 的面纱。
一、先搞懂:什么是 "空间变换"?
我们生活在 3D 空间,屏幕是 2D 空间,甚至可以抽象出 1D 直线空间。空间变换,就是对空间中的 "点" 或 "向量" 做 "改造"------ 比如移动位置、放大缩小、旋转方向、拉伸变形等。
举几个直观例子(以 2D 平面为例):
- 把一张照片放大 2 倍(缩放变换);
- 把手机屏幕顺时针转 90 度(旋转变换);
- 把一个正方形拉成平行四边形(剪切变换);
- 把地图上的点从北京移到上海(平移变换)。
这些看似不同的操作,都可以用统一的数学工具 ------矩阵来描述。而其中最基础、最核心的是 "线性变换",矩阵与线性变换几乎是 "一一对应" 的关系。
二、铺垫:变换的对象 ------ 向量与坐标
要谈变换,先明确 "变换什么"。空间中的点或物体,都可以用 "向量" 表示:

向量的核心是 "方向" 和 "长度",而空间变换的本质,就是改变向量的方向、长度,或同时改变两者。
关键前提:线性变换的两个规则(矩阵直接对应的是线性变换):
- 保持原点不变(比如旋转、缩放不会让原点移位,但平移会,所以平移不是线性变换);
- 保持 "线性组合" 不变 ------ 简单说,空间中的网格线变换后依然平行且等距(比如不会把直线变曲线)。
只要满足这两个规则,这个变换就是线性变换,一定能找到一个矩阵来表示它;反之,一个矩阵也一定对应一个线性变换。
三、核心桥梁:矩阵如何 "描述" 线性变换?
这是理解 "矩阵魔术" 的关键 ------矩阵的列,就是空间 "基向量" 变换后的结果。
1. 什么是 "基向量"?
空间的 "基向量",是构建空间的 "基本单位"。比如 2D 平面,我们最熟悉的基向量是:

2. 基向量变了,所有向量都变了
线性变换的规则决定了:只要知道基向量\(\vec{i}\)和\(\vec{j}\)变换后的结果,就能推导出所有向量的变换结果。
比如,假设一个线性变换把基向量变成:

3. 矩阵登场:把基向量的变换结果 "装" 进矩阵

这就是矩阵与线性变换的核心关系:
矩阵是线性变换的 "数学编码",矩阵的列是基向量变换后的坐标,矩阵与向量的乘法是 "应用这个变换"。
从此以后,"对向量做线性变换" 和 "用矩阵乘向量" 就成了一回事 ------ 矩阵就是变换的 "操作手册"。
四、实战:常见的 "空间魔术" 与对应矩阵
我们用具体的线性变换,验证上面的结论,感受矩阵的 "魔力"。
1. 魔术 1:缩放变换(放大 / 缩小)
目标:把 2D 平面的所有向量,x 方向缩放k倍,y 方向缩放m倍。

2. 魔术 2:旋转变换(绕原点旋转)
目标:把 2D 平面的所有向量,绕原点顺时针旋转\(\theta\)角。
用三角函数推导基向量的变换(画图可直观理解):

这正是我们日常看到的 "旋转" 效果 ------ 矩阵用三角函数编码了旋转的角度。
3. 魔术 3:剪切变换(拉伸变形)
目标:把 2D 平面的向量 "斜着拉",比如 x 方向随 y 变化(水平剪切)。

这种变换常见于图像矫正(比如倾斜的文档扫描后拉正)。
五、进阶魔术:矩阵乘法 = 变换的 "组合"
如果我们想做 "先旋转,再缩放" 的复合操作,不需要单独计算两次变换 ------矩阵乘法可以表示变换的组合。
关键规则:先做变换 A,再做变换 B,对应的复合矩阵是 B×A(矩阵乘法不交换,顺序不能乱)。
例子:先旋转 90 度(矩阵 R),再 x 方向缩放 2 倍(矩阵 S)。


六、拓展:从 2D 到 3D,再到 "平移"(仿射变换)
1. 3D 空间的变换
3D 空间的线性变换(旋转、缩放、剪切),用 3×3 矩阵表示,核心逻辑和 2D 一致:
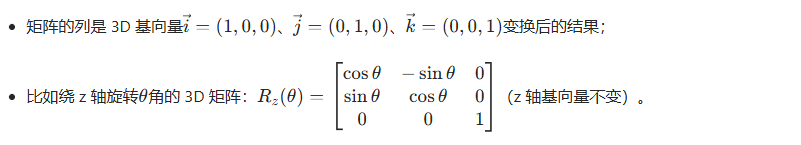
3D 矩阵的应用更广泛:比如 VR/AR 中的视角变换、3D 建模软件的模型旋转缩放。
2. 解决 "平移":仿射变换与齐次坐标

计算机图形学中,所有物体的变换(旋转 + 缩放 + 平移)都用齐次矩阵表示,一次乘法就能完成所有操作 ------ 这是矩阵 "魔术" 在工程中的核心应用。
七、深层奥秘:行列式与逆矩阵
1. 行列式:变换的 "面积 / 体积缩放因子"

3D 矩阵的行列式,是单位立方体的体积缩放因子 ------ 这解释了 "行列式为 0" 的意义:变换后空间被压缩成更低维度(比如 2D 压成直线,3D 压成平面),体积为 0,这种变换无法 "撤销"。
2. 逆矩阵:变换的 "撤销操作"

八、现实中的 "矩阵魔术" 应用
- 计算机图形学:游戏、动画中的 3D 模型变换(旋转、缩放、移动)、相机视角切换,都用齐次矩阵实现;
- 图像处理:图像的旋转、缩放、剪切矫正、镜像翻转,本质是矩阵与像素坐标的乘法;
- 机器人学:机械臂的每个关节旋转都对应一个矩阵,复合矩阵能计算末端执行器的位置,逆矩阵用于路径规划;
- 人工智能:深度学习中的卷积操作、特征变换,本质是高维空间的线性变换(矩阵乘法);
- 物理:坐标变换(比如从直角坐标到极坐标)、向量的旋转(比如力学中的力的分解)。
九、总结:矩阵是空间变换的 "通用语言"
矩阵的本质,不是数字的堆砌,而是线性变换的 "数学编码" ------ 基向量的变换决定了矩阵的形式,矩阵乘法对应变换的组合,行列式描述变换的缩放效果,逆矩阵是变换的撤销。
从 2D 平面的简单旋转,到 3D 空间的复杂动作,再到高维数据的特征变换,矩阵用统一的规则操控着空间中的一切,这就是 "空间转换魔术" 的核心 ------ 用简洁的数学工具,描述复杂的空间变化。
当你下次看到游戏角色转身、照片被旋转时,不妨想想:背后正是矩阵在默默 "施展魔法"。