(leetcode)力扣100 21搜索二维矩阵2（z型搜索）

题目

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。

每列的元素从上到下升序排列。

数据范围

m == matrix.length

n == matrix[i].length

1 <= n, m <= 300

-10⁹ <= matrix[i][j] <= 10⁹

每行的所有元素从左到右升序排列每列的所有元素从上到下升序排列

-10⁹ <= target <= 10⁹

测试用例

示例1

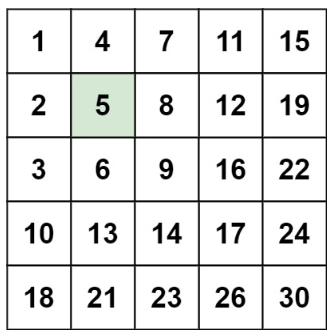
java 复制代码

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例2

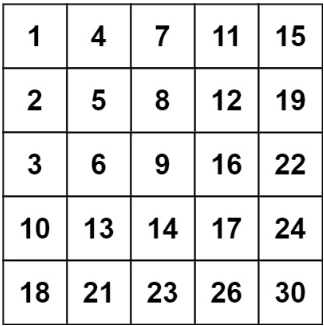
java 复制代码

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

题解（z型搜索）

java 复制代码

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int x = 0, y = n - 1;
        while (x < m && y >= 0) {
            if (matrix[x][y] == target) {
                return true;
            }
            if (matrix[x][y] > target) {
                --y;
            } else {
                ++x;
            }
        }
        return false;
    }
}

思路

这道题依然可以说不难把，就是需要一点积累，遇到这种情况要想到使用Z型搜索，具体是哪种情况一会儿会说明。博主的代码就不拿出来献丑了，确实是很少接触Z型搜索，结果写了个裁枝bfs出来，时间居然和暴力搜索一样，麻，感觉也是，这种递增矩阵bfs没有体现任何优势，最近几道题都比较简单，没有动脑了。

具体思路就引用官解了

java 复制代码

我们可以从矩阵 matrix 的右上角 (0,n−1) 进行搜索。在每一步的搜索过程中，如果我们位于位置 (x,y)，那么我们希望在以 matrix 的左下角为左下角、以 (x,y) 为右上角的矩阵中进行搜索，即行的范围为 [x,m−1]，列的范围为 [0,y]：

如果 matrix[x,y]=target，说明搜索完成；

如果 matrix[x,y]>target，由于每一列的元素都是升序排列的，那么在当前的搜索矩阵中，所有位于第 y 列的元素都是严格大于 target 的，因此我们可以将它们全部忽略，即将 y 减少 1；

如果 matrix[x,y]<target，由于每一行的元素都是升序排列的，那么在当前的搜索矩阵中，所有位于第 x 行的元素都是严格小于 target 的，因此我们可以将它们全部忽略，即将 x 增加 1。

在搜索的过程中，如果我们超出了矩阵的边界，那么说明矩阵中不存在 target。

然后是具体哪些情况需要用到z型搜索，这里做个小总结。

首先最经典的情况，就是本道题的情况，行列单调，然后我们找到可以采用的角（朝一个方向走变大，另一个方向走变小的角，例如本题的左下右上）

典型例题

LeetCode 240. 搜索二维矩阵 II

LeetCode 74. 搜索二维矩阵 I (虽然这题可以用二分，但 Z 字形同样适用)

剑指 Offer 04. 二维数组中的查找 (等同于 240 题)

乘法表中第K小的数 (部分变种思路涉及此逻辑)

第二种，很多题目表面上不是矩阵，但如果你把两个变量 iii 和 jjj 分别看作行和列，它就变成了一个隐形的有序矩阵。

典型例子：有序数组的两数之和 (Two Sum II)

虽然这是一维数组，但它的双指针收缩逻辑本质就是 Z 搜索。

假设数组 A=[2,7,11,15]A = [2, 7, 11, 15]A=[2,7,11,15]，我们要找和为 999。我们可以想象一个矩阵 M[i][j]=A[i]+A[j]M[i][j] = A[i] + A[j]M[i][j]=A[i]+A[j]。因为 AAA 是递增的，所以这个虚拟矩阵的每一行和每一列都是递增的。我们从 i=0,j=n−1i=0, j=n-1i=0,j=n−1 开始，这相当于在矩阵的右上角开始 Z 搜索。

类似题目：

三数之和：固定一个数后，剩下两个数的寻找过程就是 Z 搜索（双指针）。

平方数之和：判断 a2+b2=ca^2 + b^2 = ca2+b2=c。aaa 从 000 开始，bbb 从 c\sqrt{c}c 开始。这就是在一个无限大的行列递增矩阵中进行 Z 搜索。

此外还有
统计有序矩阵中的特定元素（划分边界 ）

Z 搜索不仅能"找一个点"，还能"画一条线"。

典型例子：统计有序矩阵中的负数 (LeetCode 1351)

给定一个每一行、每一列都按非递增顺序排列的矩阵，计算负数的个数。

逻辑：从左下角开始。如果当前值是负数，那么它右边的所有数肯定都是负数（因为行单调），直接计算数量并向上移；如果是正数，就向右移。

本质：Z 搜索在这里是用来寻找正负数的分界线。

乘法表或相似结构的第 K 小元素 (LeetCode 668/378)

这类题通常使用二分法 + Z 搜索。场景：要在 m×nm \times nm×n 的乘法表中找第 kkk 小的数。

Z 搜索的作用：当我们二分猜测一个值 XXX 时，我们需要统计矩阵中有多少个数小于 XXX。由于乘法表 i×ji \times ji×j 天然满足行列单调性，我们可以用 Z 搜索在 O(m+n)O(m+n)O(m+n) 的时间内划出分界线，统计出小于 XXX 的元素个数。

曼哈顿距离与旋转坐标系

在处理坐标系中的距离问题时，有时通过坐标转换，能把复杂的搜索变成 Z 搜索。曼哈顿距离转换为切比雪夫距离：通过将坐标 (x,y)(x, y)(x,y) 转换为 (x+y,x−y)(x+y, x-y)(x+y,x−y)，原来的菱形搜索区域会变成矩形区域。这种转换后，原本在某些距离限制下的搜索问题，有时会退化为在旋转后的单调空间里进行 Z 型过滤。