目标
- 理解回归任务与分类任务的区别
- 掌握数据预处理和特征工程的完整流程
- 构建适合回归任务的神经网络
- 使用PyTorch实现气温预测模型
- 评估回归模型的性能并可视化结果
知识铺垫
1.1 回归 vs 分类:有什么区别?
分类任务(如手写数字识别):
- 预测离散的类别
- 输出:0、1、2、3...(类别标签)
- 使用softmax + 交叉熵损失
- 准确率作为评价指标
回归任务(如气温预测):
- 预测连续的值
- 输出:25.6℃、-3.2℃、18.9℃...(具体数值)
- 使用线性输出 + MSE损失
- MAE、MSE、R²作为评价指标
💡 通俗理解:
- 分类:这是猫还是狗?(选择)
- 回归:明天多少度?(预测数值)
1.2 回归神经网络的特点
-
输出层:
- 分类:神经元数 = 类别数,用softmax
- 回归:1个神经元(单输出)或多个神经元(多输出),无激活函数(或线性激活)
-
损失函数:
- 分类:交叉熵损失(CrossEntropyLoss)
- 回归:均方误差(MSE)、平均绝对误差(MAE)
-
评估指标:
- 分类:准确率、精确率、召回率
- 回归:R²分数、MSE、MAE、RMSE
1.3 气温预测任务说明
我们将使用一个模拟的气温数据集,包含:
- 特征:月份、时间、湿度、风速、气压...
- 目标:气温值(摄氏度)
- 任务:根据气象特征预测气温
代码实践
2.1 完整项目结构
先看整个项目的结构,然后分模块详细讲解:
python
# 气温预测回归任务完整代码框架
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
# 1. 数据加载与预处理
# 2. 神经网络模型定义
# 3. 训练函数
# 4. 评估函数
# 5. 可视化结果第一部分:数据准备与预处理
3.1 生成模拟气温数据
由于真实气象数据获取复杂,先创建一个模拟数据集:
python
def generate_temperature_data(n_samples=1000):
"""
生成模拟气温数据
参数:
n_samples: 样本数量
返回:
DataFrame格式的数据
"""
np.random.seed(42) # 设置随机种子,保证可重复性
# 生成特征
data = {
'month': np.random.randint(1, 13, n_samples), # 月份 1-12
'hour': np.random.randint(0, 24, n_samples), # 小时 0-23
'humidity': np.random.uniform(30, 90, n_samples), # 湿度 30-90%
'wind_speed': np.random.uniform(0, 15, n_samples), # 风速 0-15 m/s
'pressure': np.random.uniform(980, 1030, n_samples), # 气压 980-1030 hPa
'cloud_cover': np.random.uniform(0, 1, n_samples), # 云量 0-1
}
df = pd.DataFrame(data)
# 生成目标值(气温)基于特征的简单关系
# 真实的气温受到多种因素影响,这里模拟一个非线性关系
df['temperature'] = (
15 + # 基准温度
10 * np.sin(2 * np.pi * df['month'] / 12) + # 季节影响
5 * np.sin(2 * np.pi * df['hour'] / 24) + # 昼夜影响
-0.1 * df['humidity'] + # 湿度影响
-0.3 * df['wind_speed'] + # 风速影响
0.05 * df['pressure'] + # 气压影响
-2 * df['cloud_cover'] + # 云量影响
np.random.normal(0, 2, n_samples) # 随机噪声
)
# 添加一些交互特征
df['feels_like'] = df['temperature'] - 0.5 * df['wind_speed'] * (1 - df['humidity']/100)
return df
# 生成数据
df = generate_temperature_data(2000)
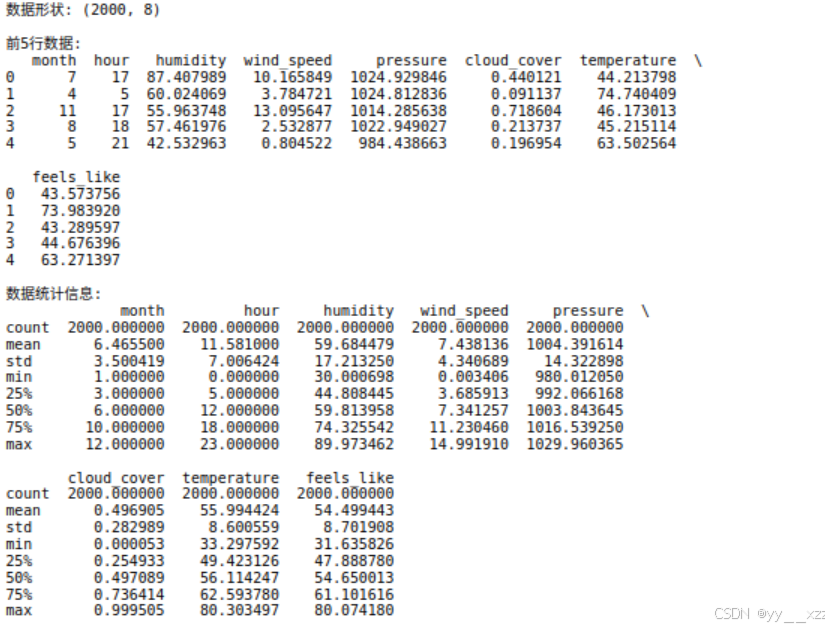
print("数据形状:", df.shape)
print("\n前5行数据:")
print(df.head())
print("\n数据统计信息:")
print(df.describe())代码解释:
np.random.seed(42):设置随机种子,保证每次生成的数据相同- 生成6个特征:月份、小时、湿度、风速、气压、云量
- 生成目标值
temperature:基于特征的组合加上一些噪声 - 添加体感温度
feels_like作为额外特征
运行:
3.2 数据探索与可视化
python
def explore_data(df):
"""数据探索和可视化"""
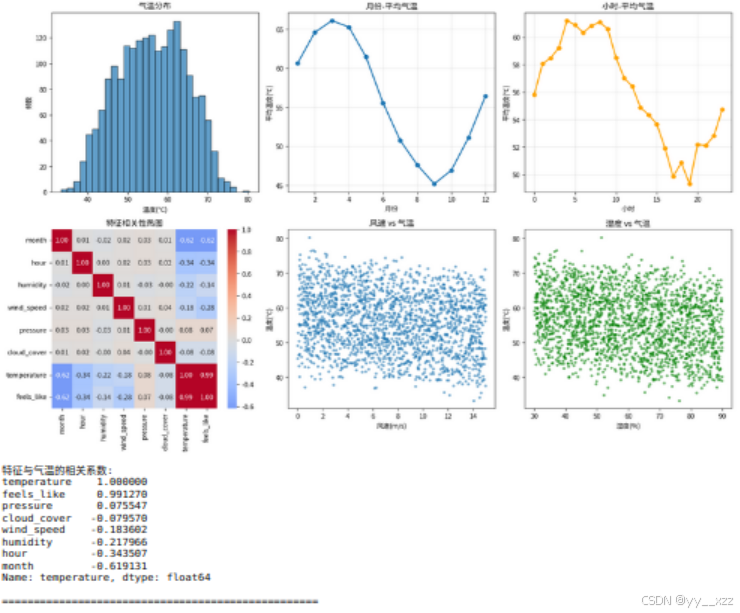
# 1. 查看目标变量分布
plt.figure(figsize=(15, 10))
plt.subplot(2, 3, 1)
plt.hist(df['temperature'], bins=30, edgecolor='black', alpha=0.7)
plt.title('气温分布')
plt.xlabel('温度(℃)')
plt.ylabel('频数')
# 2. 月份与气温关系
plt.subplot(2, 3, 2)
month_avg = df.groupby('month')['temperature'].mean()
plt.plot(month_avg.index, month_avg.values, 'o-', linewidth=2)
plt.title('月份-平均气温')
plt.xlabel('月份')
plt.ylabel('平均温度(℃)')
plt.grid(True, alpha=0.3)
# 3. 时间与气温关系
plt.subplot(2, 3, 3)
hour_avg = df.groupby('hour')['temperature'].mean()
plt.plot(hour_avg.index, hour_avg.values, 'o-', linewidth=2, color='orange')
plt.title('小时-平均气温')
plt.xlabel('小时')
plt.ylabel('平均温度(℃)')
plt.grid(True, alpha=0.3)
# 4. 相关性热图
plt.subplot(2, 3, 4)
import seaborn as sns
corr_matrix = df.corr()
sns.heatmap(corr_matrix, annot=True, fmt='.2f', cmap='coolwarm', center=0)
plt.title('特征相关性热图')
# 5. 风速与气温散点图
plt.subplot(2, 3, 5)
plt.scatter(df['wind_speed'], df['temperature'], alpha=0.5, s=10)
plt.title('风速 vs 气温')
plt.xlabel('风速(m/s)')
plt.ylabel('温度(℃)')
# 6. 湿度与气温散点图
plt.subplot(2, 3, 6)
plt.scatter(df['humidity'], df['temperature'], alpha=0.5, s=10, color='green')
plt.title('湿度 vs 气温')
plt.xlabel('湿度(%)')
plt.ylabel('温度(℃)')
plt.tight_layout()
plt.show()
# 打印相关系数
print("特征与气温的相关系数:")
print(df.corr()['temperature'].sort_values(ascending=False))
print("\n" + "="*50)
# 运行数据探索
explore_data(df)数据探索的重要性:
- 发现异常值:数据是否有异常温度值
- 理解关系:哪些特征与气温强相关
- 检查分布:数据是否需要归一化
- 验证逻辑:月份-气温关系是否符合常识
运行:
3.3 数据预处理
python
def prepare_data(df, test_size=0.2, random_state=42):
"""
数据预处理流程
步骤:1.特征选择 2.分割 3.标准化 4.转换为Tensor
"""
# 1. 分离特征和目标
# 选择特征(排除目标列和可能泄露信息的列)
feature_cols = ['month', 'hour', 'humidity', 'wind_speed', 'pressure', 'cloud_cover']
X = df[feature_cols].values # 转换为numpy数组
y = df['temperature'].values.reshape(-1, 1) # 保持二维形状 (n_samples, 1)
print(f"特征形状: {X.shape}, 目标形状: {y.shape}")
# 2. 分割训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=test_size, random_state=random_state
)
print(f"训练集: {X_train.shape}, 测试集: {X_test.shape}")
# 3. 特征标准化(非常重要!)
# 回归任务中,特征的尺度差异会影响梯度下降
scaler_X = StandardScaler()
X_train_scaled = scaler_X.fit_transform(X_train)
X_test_scaled = scaler_X.transform(X_test) # 注意:用训练集的参数转换测试集
scaler_y = StandardScaler()
y_train_scaled = scaler_y.fit_transform(y_train)
y_test_scaled = scaler_y.transform(y_test)
print("\n标准化后的统计信息:")
print(f"X_train - 均值: {X_train_scaled.mean():.2f}, 标准差: {X_train_scaled.std():.2f}")
print(f"y_train - 均值: {y_train_scaled.mean():.2f}, 标准差: {y_train_scaled.std():.2f}")
# 4. 转换为PyTorch Tensor
X_train_tensor = torch.FloatTensor(X_train_scaled)
y_train_tensor = torch.FloatTensor(y_train_scaled)
X_test_tensor = torch.FloatTensor(X_test_scaled)
y_test_tensor = torch.FloatTensor(y_test_scaled)
return {
'X_train': X_train_tensor,
'y_train': y_train_tensor,
'X_test': X_test_tensor,
'y_test': y_test_tensor,
'scaler_X': scaler_X,
'scaler_y': scaler_y,
'feature_names': feature_cols
}
# 执行数据预处理
data_dict = prepare_data(df)
print("\n" + "="*50)
print("数据预处理完成!")预处理关键点:
-
为什么需要标准化?
- 特征尺度不同(月份1-12,湿度30-90)
- 标准化后所有特征均值为0,方差为1
- 帮助梯度下降更快收敛
-
为什么用训练集参数标准化测试集?
- 防止数据泄露(data leakage)
- 测试集应该模拟真实情况,不能"看到"训练集的信息
-
为什么目标值也要标准化?
- 加速训练收敛
- 使用标准化后的目标值,最后再反标准化回原始尺度
运行:

第二部分:神经网络模型设计
4.1 回归神经网络模型
python
class TemperaturePredictor(nn.Module):
"""
气温预测神经网络
回归任务的特点:
1. 输出层没有激活函数(或使用线性激活)
2. 输出维度为1(预测单个连续值)
"""
def __init__(self, input_size, hidden_sizes=[64, 32, 16]):
"""
参数:
input_size: 输入特征数量
hidden_sizes: 隐藏层神经元数量列表
"""
super(TemperaturePredictor, self).__init__()
# 动态构建网络层
layers = []
prev_size = input_size
# 添加隐藏层
for i, hidden_size in enumerate(hidden_sizes):
layers.append(nn.Linear(prev_size, hidden_size))
layers.append(nn.ReLU()) # 隐藏层使用ReLU激活
layers.append(nn.BatchNorm1d(hidden_size)) # 批归一化,加速训练
layers.append(nn.Dropout(0.2)) # Dropout防止过拟合
prev_size = hidden_size
# 输出层:线性层,无激活函数(回归任务)
layers.append(nn.Linear(prev_size, 1))
# 将层列表转换为Sequential模型
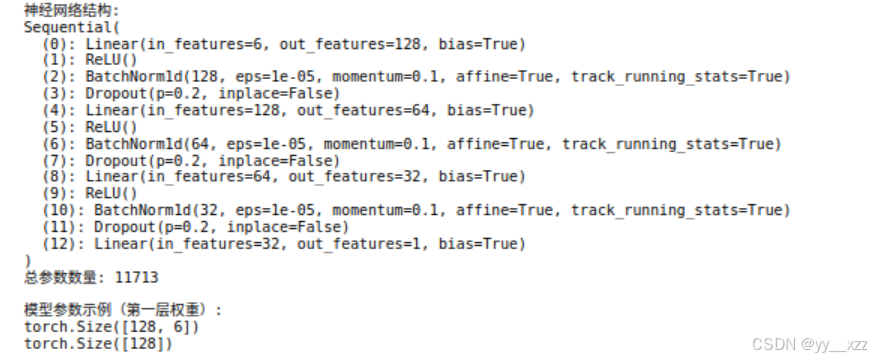
self.network = nn.Sequential(*layers)
# 打印网络结构
print("神经网络结构:")
print(self.network)
print(f"总参数数量: {sum(p.numel() for p in self.parameters())}")
def forward(self, x):
"""前向传播"""
return self.network(x)
# 创建模型实例
input_size = len(data_dict['feature_names'])
model = TemperaturePredictor(input_size=input_size, hidden_sizes=[128, 64, 32])
# 检查模型
print("\n模型参数示例(第一层权重):")
print(model.network[0].weight.shape) # 第一层线性层的权重形状
print(model.network[0].bias.shape) # 第一层线性层的偏置形状回归模型设计要点:
- 输出层 :
nn.Linear(prev_size, 1),无激活函数 - 激活函数:隐藏层用ReLU,输出层不用激活函数
- 批归一化 :
nn.BatchNorm1d(),加速收敛,提高稳定性 - Dropout:防止过拟合,训练时随机"关闭"一些神经元
运行:
4.2 损失函数与优化器
python
def setup_training(model, learning_rate=0.001):
"""设置训练组件:损失函数和优化器"""
# 1. 损失函数 - 回归任务常用MSE
# MSE = 平均(预测值 - 真实值)^2
criterion = nn.MSELoss()
# 也可以尝试L1损失(对异常值不敏感)
# criterion = nn.L1Loss()
# 2. 优化器 - Adam优化器
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
# 3. 学习率调度器(可选)
scheduler = optim.lr_scheduler.ReduceLROnPlateau(
optimizer, mode='min', factor=0.5, patience=10, verbose=True
)
print(f"使用损失函数: {criterion.__class__.__name__}")
print(f"使用优化器: {optimizer.__class__.__name__}, 学习率: {learning_rate}")
return criterion, optimizer, scheduler
# 设置训练组件
criterion, optimizer, scheduler = setup_training(model)损失函数选择:
- MSE(均方误差):对异常值敏感,惩罚大误差
- MAE(平均绝对误差):对异常值不敏感,更稳健
- Huber损失:MSE和MAE的结合,对异常值有一定鲁棒性
第三部分:模型训练
5.1 训练循环实现
python
def train_model(model, data_dict, criterion, optimizer, scheduler,
n_epochs=200, batch_size=32, early_stopping_patience=20):
"""
训练回归模型
包含:训练循环、验证、早停、学习率调整
"""
X_train, y_train = data_dict['X_train'], data_dict['y_train']
X_test, y_test = data_dict['X_test'], data_dict['y_test']
# 数据加载器
from torch.utils.data import TensorDataset, DataLoader
train_dataset = TensorDataset(X_train, y_train)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
# 记录训练历史
history = {
'train_loss': [],
'val_loss': [],
'learning_rate': []
}
# 早停相关变量
best_val_loss = float('inf')
patience_counter = 0
best_model_state = None
print("开始训练...")
print("="*60)
for epoch in range(n_epochs):
# 训练阶段
model.train() # 设置为训练模式(启用Dropout、BatchNorm更新)
train_loss = 0.0
for batch_X, batch_y in train_loader:
# 梯度清零
optimizer.zero_grad()
# 前向传播
outputs = model(batch_X)
loss = criterion(outputs, batch_y)
# 反向传播
loss.backward()
# 梯度裁剪(防止梯度爆炸)
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
# 更新权重
optimizer.step()
train_loss += loss.item() * batch_X.size(0)
# 计算平均训练损失
train_loss = train_loss / len(train_loader.dataset)
# 验证阶段
model.eval() # 设置为评估模式(禁用Dropout、固定BatchNorm)
with torch.no_grad():
val_outputs = model(X_test)
val_loss = criterion(val_outputs, y_test).item()
# 记录历史
history['train_loss'].append(train_loss)
history['val_loss'].append(val_loss)
history['learning_rate'].append(optimizer.param_groups[0]['lr'])
# 学习率调整
scheduler.step(val_loss)
# 早停检查
if val_loss < best_val_loss:
best_val_loss = val_loss
patience_counter = 0
best_model_state = model.state_dict().copy() # 保存最佳模型
else:
patience_counter += 1
# 打印进度
if (epoch + 1) % 20 == 0:
print(f"Epoch [{epoch+1:03d}/{n_epochs}] | "
f"Train Loss: {train_loss:.4f} | "
f"Val Loss: {val_loss:.4f} | "
f"LR: {optimizer.param_groups[0]['lr']:.6f}")
# 早停判断
if patience_counter >= early_stopping_patience:
print(f"\n早停触发!在epoch {epoch+1}停止训练。")
break
# 加载最佳模型
if best_model_state is not None:
model.load_state_dict(best_model_state)
print("="*60)
print(f"训练完成!最佳验证损失: {best_val_loss:.4f}")
return model, history
# 开始训练
trained_model, history = train_model(
model=model,
data_dict=data_dict,
criterion=criterion,
optimizer=optimizer,
scheduler=scheduler,
n_epochs=200,
batch_size=64
)训练技巧详解:
-
model.train() / model.eval():
train():启用Dropout和BatchNorm的统计更新eval():禁用Dropout,固定BatchNorm的统计
-
梯度裁剪 :
clip_grad_norm_- 防止梯度爆炸(gradient explosion)
- 限制梯度向量的最大范数
-
早停(Early Stopping):
- 当验证损失不再改善时停止训练
- 防止过拟合,节省训练时间
-
学习率调度:
- 当验证损失平台期时降低学习率
- 帮助模型跳出局部最小值
运行:

5.2 训练过程可视化
python
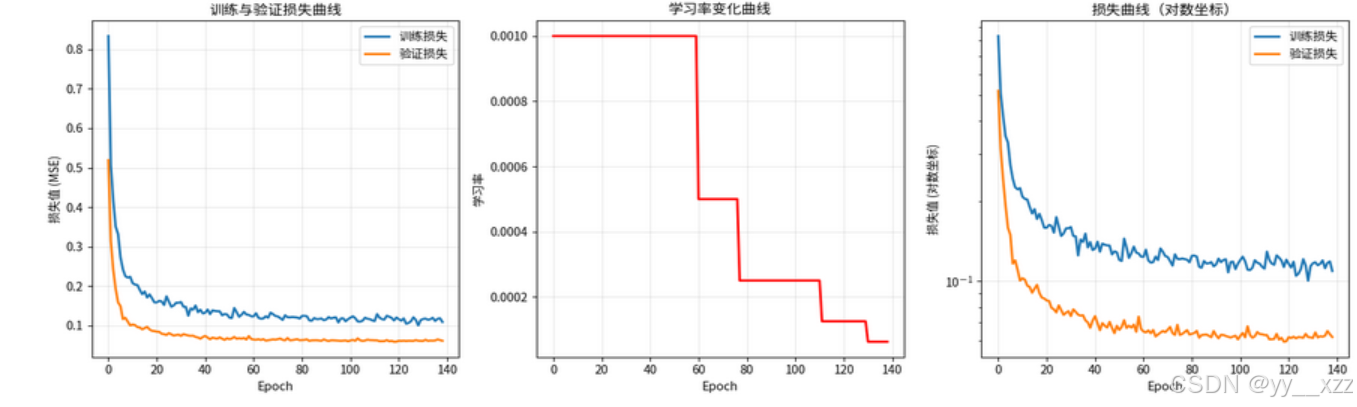
def plot_training_history(history):
"""可视化训练过程"""
plt.figure(figsize=(15, 5))
# 1. 损失曲线
plt.subplot(1, 3, 1)
plt.plot(history['train_loss'], label='训练损失', linewidth=2)
plt.plot(history['val_loss'], label='验证损失', linewidth=2)
plt.xlabel('Epoch')
plt.ylabel('损失值 (MSE)')
plt.title('训练与验证损失曲线')
plt.legend()
plt.grid(True, alpha=0.3)
# 2. 学习率变化
plt.subplot(1, 3, 2)
plt.plot(history['learning_rate'], color='red', linewidth=2)
plt.xlabel('Epoch')
plt.ylabel('学习率')
plt.title('学习率变化曲线')
plt.grid(True, alpha=0.3)
# 3. 损失对数坐标
plt.subplot(1, 3, 3)
plt.semilogy(history['train_loss'], label='训练损失', linewidth=2)
plt.semilogy(history['val_loss'], label='验证损失', linewidth=2)
plt.xlabel('Epoch')
plt.ylabel('损失值 (对数坐标)')
plt.title('损失曲线(对数坐标)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 绘制训练历史
plot_training_history(history)运行:
第四部分:模型评估与预测
6.1 模型评估函数
python
def evaluate_model(model, data_dict, scaler_y):
"""
全面评估回归模型性能
返回:评估指标和预测结果
"""
model.eval()
X_test, y_test = data_dict['X_test'], data_dict['y_test']
with torch.no_grad():
# 预测
predictions_scaled = model(X_test)
# 反标准化到原始尺度
predictions = scaler_y.inverse_transform(predictions_scaled.numpy())
y_test_original = scaler_y.inverse_transform(y_test.numpy())
# 计算评估指标
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
mse = mean_squared_error(y_test_original, predictions)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test_original, predictions)
r2 = r2_score(y_test_original, predictions)
# 计算平均绝对百分比误差 (MAPE)
mape = np.mean(np.abs((y_test_original - predictions) / y_test_original)) * 100
print("="*50)
print("模型评估结果:")
print("="*50)
print(f"均方误差 (MSE): {mse:.4f}")
print(f"均方根误差 (RMSE): {rmse:.4f} ℃")
print(f"平均绝对误差 (MAE): {mae:.4f} ℃")
print(f"平均绝对百分比误差 (MAPE): {mape:.2f}%")
print(f"R²分数: {r2:.4f}")
print("="*50)
# 解释R²分数
if r2 > 0.8:
print("✅ 优秀!模型能解释80%以上的数据变异")
elif r2 > 0.6:
print("👍 良好!模型有不错的预测能力")
elif r2 > 0.4:
print("📊 一般!模型有基本预测能力")
else:
print("⚠️ 需要改进!模型预测能力有限")
return {
'predictions': predictions,
'true_values': y_test_original,
'metrics': {
'MSE': mse,
'RMSE': rmse,
'MAE': mae,
'MAPE': mape,
'R2': r2
}
}
# 评估模型
evaluation = evaluate_model(trained_model, data_dict, data_dict['scaler_y'])回归评估指标解读:
- MSE/RMSE:对异常值敏感,值越小越好
- MAE:更稳健的指标,值越小越好
- R²分数:模型解释的方差比例,0-1之间,越大越好
- MAPE:百分比误差,直观但要求目标值不为0
运行:

6.2 预测结果可视化
python
def visualize_predictions(evaluation, n_samples=50):
"""可视化预测结果"""
predictions = evaluation['predictions'].flatten()
true_values = evaluation['true_values'].flatten()
plt.figure(figsize=(15, 10))
# 1. 预测值 vs 真实值散点图
plt.subplot(2, 3, 1)
plt.scatter(true_values, predictions, alpha=0.5, s=20)
# 绘制理想预测线(y=x)
min_val = min(true_values.min(), predictions.min())
max_val = max(true_values.max(), predictions.max())
plt.plot([min_val, max_val], [min_val, max_val],
'r--', linewidth=2, label='理想预测线')
plt.xlabel('真实温度 (℃)')
plt.ylabel('预测温度 (℃)')
plt.title('预测值 vs 真实值')
plt.legend()
plt.grid(True, alpha=0.3)
# 2. 残差图
plt.subplot(2, 3, 2)
residuals = true_values - predictions
plt.scatter(predictions, residuals, alpha=0.5, s=20)
plt.axhline(y=0, color='r', linestyle='--', linewidth=2)
plt.xlabel('预测温度 (℃)')
plt.ylabel('残差 (真实-预测)')
plt.title('残差图')
plt.grid(True, alpha=0.3)
# 3. 误差分布直方图
plt.subplot(2, 3, 3)
plt.hist(residuals, bins=30, edgecolor='black', alpha=0.7)
plt.axvline(x=0, color='r', linestyle='--', linewidth=2)
plt.xlabel('预测误差 (℃)')
plt.ylabel('频数')
plt.title('预测误差分布')
# 4. 前50个样本对比
plt.subplot(2, 3, 4)
sample_indices = np.arange(min(n_samples, len(true_values)))
plt.plot(sample_indices, true_values[:n_samples],
'o-', label='真实值', linewidth=2, markersize=6)
plt.plot(sample_indices, predictions[:n_samples],
's-', label='预测值', linewidth=2, markersize=6)
plt.xlabel('样本索引')
plt.ylabel('温度 (℃)')
plt.title(f'前{n_samples}个样本对比')
plt.legend()
plt.grid(True, alpha=0.3)
# 5. 累积分布函数
plt.subplot(2, 3, 5)
sorted_residuals = np.sort(np.abs(residuals))
cdf = np.arange(1, len(sorted_residuals) + 1) / len(sorted_residuals)
plt.plot(sorted_residuals, cdf, linewidth=2)
plt.xlabel('绝对误差 (℃)')
plt.ylabel('累积概率')
plt.title('误差累积分布函数')
plt.grid(True, alpha=0.3)
# 添加误差统计
plt.axvline(x=np.percentile(np.abs(residuals), 50),
color='r', linestyle='--', alpha=0.7, label='中位数误差')
plt.axvline(x=np.percentile(np.abs(residuals), 90),
color='g', linestyle='--', alpha=0.7, label='90%分位数')
plt.legend()
# 6. 按温度区间的误差分析
plt.subplot(2, 3, 6)
temperature_bins = np.linspace(true_values.min(), true_values.max(), 6)
bin_errors = []
bin_labels = []
for i in range(len(temperature_bins)-1):
mask = (true_values >= temperature_bins[i]) & (true_values < temperature_bins[i+1])
if np.sum(mask) > 0:
bin_error = np.mean(np.abs(residuals[mask]))
bin_errors.append(bin_error)
bin_labels.append(f'{temperature_bins[i]:.0f}-{temperature_bins[i+1]:.0f}')
bars = plt.bar(bin_labels, bin_errors, alpha=0.7, color='skyblue')
plt.xlabel('温度区间 (℃)')
plt.ylabel('平均绝对误差 (℃)')
plt.title('不同温度区间的预测误差')
# 在柱子上添加数值
for bar, error in zip(bars, bin_errors):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.05,
f'{error:.2f}', ha='center', va='bottom')
plt.xticks(rotation=45)
plt.tight_layout()
plt.show()
# 打印详细统计
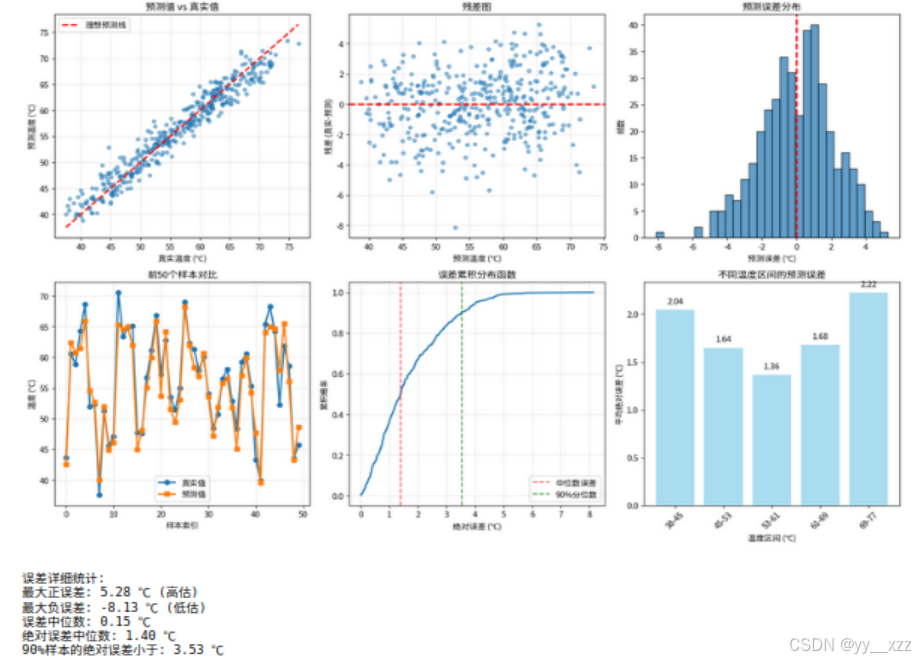
print("\n误差详细统计:")
print(f"最大正误差: {residuals.max():.2f} ℃ (高估)")
print(f"最大负误差: {residuals.min():.2f} ℃ (低估)")
print(f"误差中位数: {np.median(residuals):.2f} ℃")
print(f"绝对误差中位数: {np.median(np.abs(residuals)):.2f} ℃")
print(f"90%样本的绝对误差小于: {np.percentile(np.abs(residuals), 90):.2f} ℃")
# 可视化预测结果
visualize_predictions(evaluation, n_samples=50)运行:
6.3 特征重要性分析
python
def analyze_feature_importance(model, data_dict):
"""分析特征重要性(使用简单的扰动方法)"""
model.eval()
X_test = data_dict['X_test']
feature_names = data_dict['feature_names']
with torch.no_grad():
# 基准预测
baseline_pred = model(X_test)
baseline_loss = criterion(baseline_pred, data_dict['y_test']).item()
feature_importance = []
# 对每个特征添加噪声,看损失变化
for i in range(X_test.shape[1]):
X_perturbed = X_test.clone()
# 添加噪声(标准差为原始特征标准差的0.2倍)
X_perturbed[:, i] += torch.randn_like(X_perturbed[:, i]) * 0.2
perturbed_pred = model(X_perturbed)
perturbed_loss = criterion(perturbed_pred, data_dict['y_test']).item()
# 损失增加越多,特征越重要
importance = (perturbed_loss - baseline_loss) / baseline_loss * 100
feature_importance.append(importance)
# 创建重要性DataFrame
importance_df = pd.DataFrame({
'特征': feature_names,
'重要性(%)': feature_importance
}).sort_values('重要性(%)', ascending=False)
# 可视化
plt.figure(figsize=(10, 6))
bars = plt.barh(range(len(importance_df)),
importance_df['重要性(%)'],
color='steelblue')
plt.xlabel('重要性 (%)')
plt.title('特征重要性分析')
plt.yticks(range(len(importance_df)), importance_df['特征'])
# 添加数值标签
for i, (bar, imp) in enumerate(zip(bars, importance_df['重要性(%)'])):
plt.text(bar.get_width() + 0.1, bar.get_y() + bar.get_height()/2,
f'{imp:.1f}%', va='center')
plt.grid(True, alpha=0.3, axis='x')
plt.tight_layout()
plt.show()
return importance_df
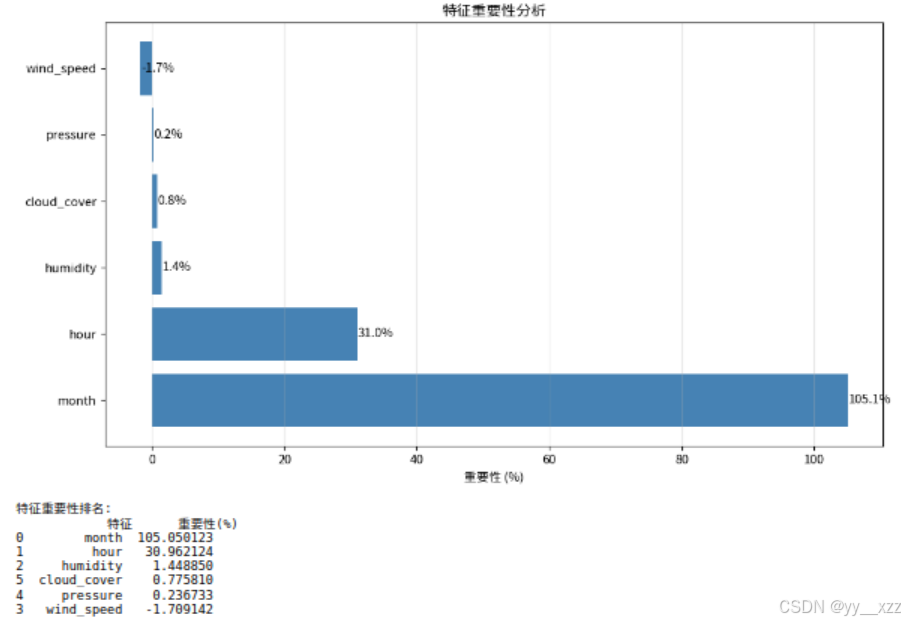
# 分析特征重要性
importance_df = analyze_feature_importance(trained_model, data_dict)
print("特征重要性排名:")
print(importance_df)运行:
第五部分:模型保存与应用
7.1 保存和加载模型
python
def save_model(model, data_dict, evaluation, filepath='temperature_predictor.pth'):
"""保存完整模型和相关数据"""
import pickle
save_data = {
'model_state_dict': model.state_dict(),
'model_architecture': {
'input_size': len(data_dict['feature_names']),
'hidden_sizes': [128, 64, 32] # 与模型定义一致
},
'scalers': {
'X': data_dict['scaler_X'],
'y': data_dict['scaler_y']
},
'feature_names': data_dict['feature_names'],
'evaluation_metrics': evaluation['metrics'],
'training_info': {
'best_val_loss': min(history['val_loss']),
'final_epoch': len(history['val_loss'])
}
}
# 保存模型权重
torch.save(model.state_dict(), filepath)
# 保存完整配置
config_file = filepath.replace('.pth', '_config.pkl')
with open(config_file, 'wb') as f:
pickle.dump(save_data, f)
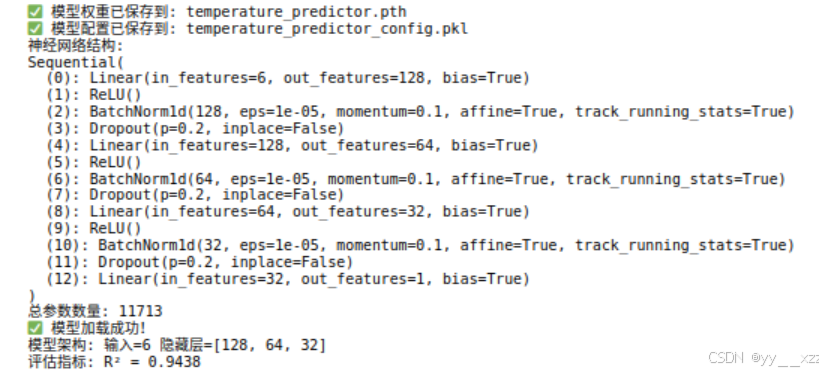
print(f"✅ 模型权重已保存到: {filepath}")
print(f"✅ 模型配置已保存到: {config_file}")
return filepath, config_file
def load_model(filepath='temperature_predictor.pth'):
"""加载已保存的模型"""
import pickle
# 加载配置
config_file = filepath.replace('.pth', '_config.pkl')
with open(config_file, 'rb') as f:
save_data = pickle.load(f)
# 创建模型实例
model = TemperaturePredictor(
input_size=save_data['model_architecture']['input_size'],
hidden_sizes=save_data['model_architecture']['hidden_sizes']
)
# 加载权重
model.load_state_dict(torch.load(filepath))
model.eval()
print("✅ 模型加载成功!")
print(f"模型架构: 输入={save_data['model_architecture']['input_size']} "
f"隐藏层={save_data['model_architecture']['hidden_sizes']}")
print(f"评估指标: R² = {save_data['evaluation_metrics']['R2']:.4f}")
return model, save_data
# 保存模型
model_path, config_path = save_model(trained_model, data_dict, evaluation)
# 加载模型(演示)
loaded_model, loaded_data = load_model(model_path)运行:
7.2 实际预测应用
python
def predict_temperature(model, scalers, feature_names, new_data):
"""
使用训练好的模型进行新数据预测
参数:
new_data: DataFrame或字典,包含所有特征
返回:
预测的温度值
"""
# 确保是DataFrame格式
if isinstance(new_data, dict):
new_data = pd.DataFrame([new_data])
# 确保包含所有必要特征
missing_features = set(feature_names) - set(new_data.columns)
if missing_features:
raise ValueError(f"缺少特征: {missing_features}")
# 提取特征并转换为numpy
X_new = new_data[feature_names].values
# 标准化(使用训练时的scaler)
X_new_scaled = scalers['X'].transform(X_new)
# 转换为Tensor
X_new_tensor = torch.FloatTensor(X_new_scaled)
# 预测
model.eval()
with torch.no_grad():
predictions_scaled = model(X_new_tensor)
# 反标准化到原始尺度
predictions = scalers['y'].inverse_transform(predictions_scaled.numpy())
return predictions.flatten()
# 示例:使用模型进行预测
print("\n" + "="*50)
print("示例预测:")
print("="*50)
# 创建一些新数据
new_samples = pd.DataFrame({
'month': [6, 12, 3], # 6月、12月、3月
'hour': [14, 8, 20], # 下午2点、早上8点、晚上8点
'humidity': [65, 45, 80], # 湿度
'wind_speed': [3, 10, 5], # 风速
'pressure': [1013, 1020, 1005], # 气压
'cloud_cover': [0.2, 0.8, 0.5] # 云量
})
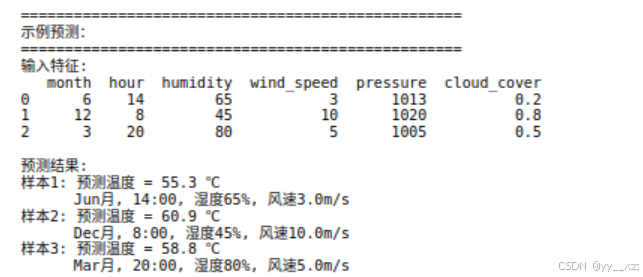
print("输入特征:")
print(new_samples)
# 进行预测
predictions = predict_temperature(
model=trained_model,
scalers={'X': data_dict['scaler_X'], 'y': data_dict['scaler_y']},
feature_names=data_dict['feature_names'],
new_data=new_samples
)
print("\n预测结果:")
month_names = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun',
'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']
for i, pred in enumerate(predictions):
print(f"样本{i+1}: 预测温度 = {pred:.1f} ℃")
# 修复:确保获取的值是Python整数
month_val = int(new_samples.iloc[i]['month']) # 转换为int
month_idx = month_val - 1
hour_val = int(new_samples.iloc[i]['hour'])
humidity_val = int(new_samples.iloc[i]['humidity'])
wind_speed_val = new_samples.iloc[i]['wind_speed']
print(f" {month_names[month_idx]}月, "
f"{hour_val}:00, "
f"湿度{humidity_val}%, "
f"风速{wind_speed_val}m/s")运行:
常见问题与解决方案
Q1: 模型预测结果都是同一个值?
原因:
- 学习率太大导致梯度爆炸
- 数据没有标准化
- 网络太深导致梯度消失
解决方案:
- 减小学习率(如0.0001)
- 检查并实施数据标准化
- 使用BatchNorm和合适的激活函数
Q2: R²分数为负值怎么办?
原因:模型预测效果比简单使用均值还差
解决方案:
- 检查数据预处理是否正确
- 降低模型复杂度(减少层数或神经元数)
- 增加训练数据或使用数据增强
- 检查是否有数据泄露
Q3: 训练损失下降但验证损失上升?
原因:过拟合(模型记住了训练数据但泛化能力差)
解决方案:
- 增加Dropout比例
- 使用L2正则化(权重衰减)
- 获取更多训练数据
- 使用早停(Early Stopping)
- 简化模型结构
Q4: 如何选择隐藏层的数量和大小?
经验法则:
- 从简单开始:1-3个隐藏层
- 神经元数量:输入层和输出层之间的值
- 逐步增加直到性能不再提升
- 使用交叉验证选择最佳结构
总结与练习
核心知识点回顾:
- 数据预处理:标准化、分割、Tensor转换
- 回归模型设计:输出层无激活函数,使用MSE损失
- 训练技巧:BatchNorm、Dropout、梯度裁剪、早停
- 评估指标:MSE、MAE、R²、可视化分析
- 模型部署:保存、加载、新数据预测
扩展练习:
练习1:优化模型性能
python
# 尝试不同的网络结构
configs = [
{'hidden_sizes': [64, 32], 'dropout': 0.1},
{'hidden_sizes': [128, 64, 32], 'dropout': 0.2},
{'hidden_sizes': [256, 128, 64, 32], 'dropout': 0.3},
]
# 比较不同配置的性能,找到最佳组合练习2:添加更多特征
python
# 1. 添加多项式特征
from sklearn.preprocessing import PolynomialFeatures
# 2. 添加交互特征(如温度×湿度)
df['temp_humidity_interaction'] = df['temperature'] * df['humidity']
# 3. 添加时间特征(如是否周末、季节)练习3:尝试不同的损失函数
python
# 比较MSE、MAE、Huber损失的效果
loss_functions = {
'MSE': nn.MSELoss(),
'MAE': nn.L1Loss(),
'Huber': nn.SmoothL1Loss(beta=1.0) # Huber损失
}
# 分别训练并比较结果练习4:超参数调优
python
# 使用网格搜索或随机搜索优化:
# 1. 学习率 [0.001, 0.0005, 0.0001]
# 2. 批大小 [16, 32, 64]
# 3. 隐藏层结构
# 4. Dropout比例 [0.1, 0.2, 0.3]