在机器人运动学建模领域,D-H(Denavit-Hartenberg)参数法绝对是绕不开的核心技术。它以极简的4个参数,就能清晰描述机械臂各连杆间的相对位姿关系,是实现正运动学求解、轨迹规划的基础。本文将从理论原理出发,一步步拆解六轴机械臂的D-H法建模流程,最后结合代码实现让理论落地,适合机器人初学者或技术爱好者深入学习。
一、为什么选择D-H法?------ 机械臂建模的"通用语言"
六轴机械臂作为工业场景中最常用的机器人构型,其连杆与关节的空间关系复杂。如果直接用三维坐标系叠加计算,不仅公式繁琐,还容易出现坐标混乱的问题。而D-H法的核心优势的在于"标准化":
- 简化参数:用仅4个参数(关节角、连杆偏移、连杆长度、连杆扭转角)描述相邻连杆的位姿,替代复杂的三维坐标变换;
- 通用性强:适用于所有串联机械臂,无论是六轴、四轴还是协作机械臂,都能套用同一套建模逻辑;
- 计算高效:通过齐次变换矩阵的乘积,可快速求解末端执行器相对于基坐标系的位姿,为后续运动学分析奠定基础。
简单来说,学会D-H法,就掌握了串联机械臂建模的"通用语言"。
二、D-H法核心:4个参数+1个变换矩阵
在D-H法中,我们需要为机械臂的每个连杆和关节建立坐标系(通常称为"D-H坐标系"),然后通过4个参数描述相邻坐标系间的变换关系,最终通过矩阵乘法得到整体变换。
1. 先搞懂:4个核心参数的定义
D-H法的4个参数是基于相邻两个关节坐标系(第i-1个关节坐标系和第i个关节坐标系)定义的,核心逻辑是"从坐标系i-1到坐标系i的变换需要4个步骤",每个步骤对应一个参数:
|-----------|-------|--------------------------|---------------------------|
| 参数符号 | 参数名称 | 核心定义 | 补充说明 |
| θᵢ(Theta) | 关节角 | 绕zᵢ₋₁轴旋转,使xᵢ₋₁轴与xᵢ轴平行的角度 | 旋转关节为变量(随关节运动变化),移动关节为常量 |
| dᵢ(d) | 连杆偏移 | 沿zᵢ₋₁轴移动,使xᵢ₋₁轴与xᵢ轴重合的距离 | 移动关节为变量,旋转关节为常量(机械臂结构固定值) |
| aᵢ(a) | 连杆长度 | 沿xᵢ轴移动,使zᵢ₋₁轴与zᵢ轴重合的距离 | 由机械臂连杆物理结构决定,为固定值 |
| αᵢ(Alpha) | 连杆扭转角 | 绕xᵢ轴旋转,使zᵢ₋₁轴与zᵢ轴平行的角度 | 由连杆的几何形状决定,为固定值 |
|-----------------------------------------------------------------------------------|
| 关键提醒:所有参数的定义都基于"相邻两个坐标系",核心是"让两个坐标系逐步重合"------先旋转z轴,再平移z轴,接着平移x轴,最后旋转x轴,四步完成坐标变换。 |
2. 核心公式:相邻连杆的齐次变换矩阵
通过上述4个参数,我们可以构建出从第i-1个坐标系到第i个坐标系的齐次变换矩阵ⁱᵢ₋₁T,这个矩阵既包含了旋转变换,也包含了平移变换,公式如下:
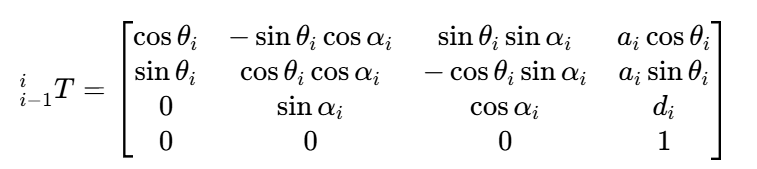
矩阵的前3行3列是旋转矩阵,描述坐标系i相对于坐标系i-1的姿态;前3行第4列是平移向量,描述坐标系i原点相对于坐标系i-1的位置;最后一行是齐次坐标的标准形式(0,0,0,1)。
3. 末端位姿求解:总变换矩阵的乘积
对于六轴机械臂,我们需要依次建立基坐标系(0号)、关节1~6的坐标系(1~6号)、末端执行器坐标系(6号,与关节6坐标系重合或固定偏移)。末端执行器相对于基坐标系的总变换矩阵⁶₀T,就是各相邻连杆变换矩阵的乘积:
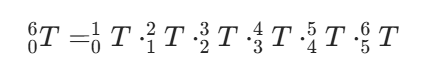
通过这个总变换矩阵,我们可以直接提取末端执行器的位置(前3行第4列)和姿态(前3行3列旋转矩阵),这就是正运动学的核心目标。
三、六轴机械臂D-H建模实战:以通用工业机械臂为例
理论讲完,我们用一个通用六轴工业机械臂(类似UR5、PUMA560构型)进行实战建模,步骤分为"建立坐标系→填写D-H参数表→计算总变换矩阵"三步。
1. 第一步:为机械臂建立D-H坐标系
建立坐标系是D-H建模的关键,需遵循严格的规则(避免参数混乱):
- z轴:与关节i的旋转轴(或移动轴)重合,方向任意(建议统一向上,方便后续计算);
- x轴:沿两个相邻z轴(zᵢ₋₁和zᵢ)的公垂线方向,指向从zᵢ₋₁到zᵢ的方向;若zᵢ₋₁与zᵢ平行,x轴垂直于z轴且指向机械臂前方;
- y轴:由右手定则确定(x×y=z),无需手动定义;
- 原点:xᵢ轴与zᵢ₋₁轴的交点;若xᵢ轴与zᵢ₋₁轴不相交,原点取zᵢ₋₁轴上的任意点(建议取关节中心,简化参数)。
按照上述规则,为六轴机械臂的每个关节建立坐标系后,我们就能直观看到各坐标系的相对位置,为填写参数表做准备。
2. 第二步:填写D-H参数表
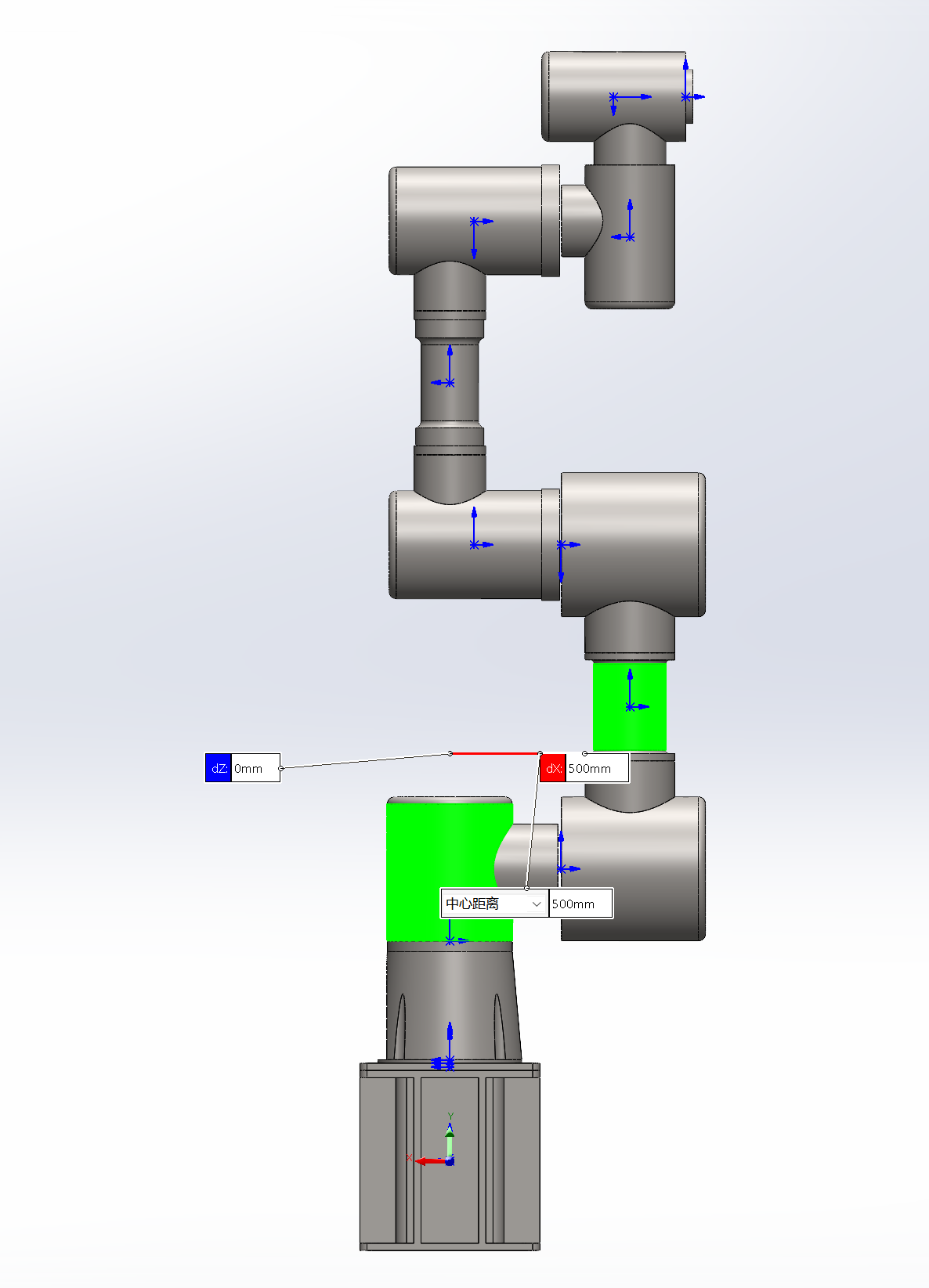
以我自己创建的机械臂模型为例,根据建立的坐标系,结合机械臂的物理结构尺寸,我们可以填写出完整的D-H参数表。
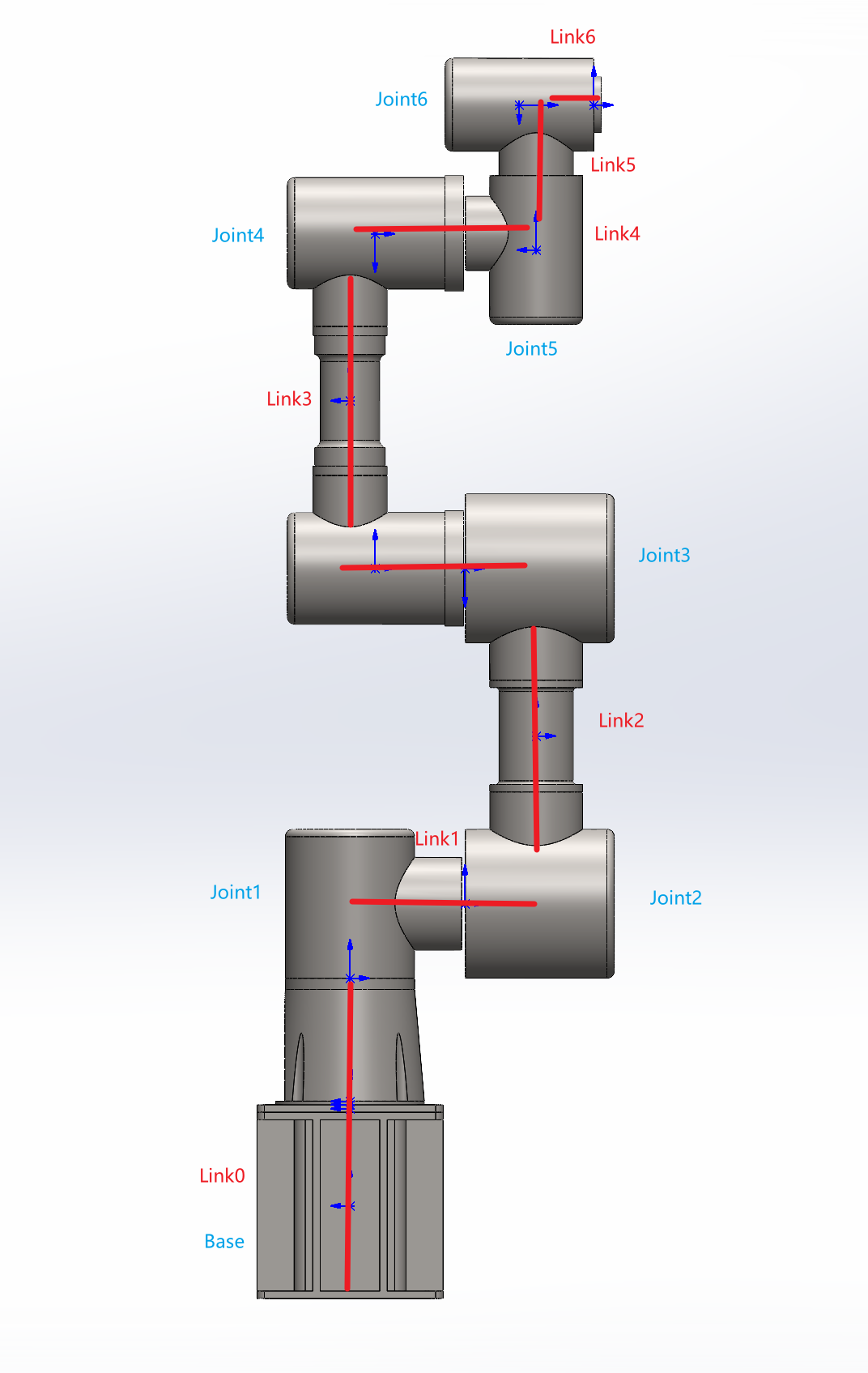
在实际研发中,我们常常需要根据自定义机械臂的结构建立参数表。例如,此自定义六轴机械臂的 D-H 参数表(含关节角零位偏移)如下:
| 连杆 i | 关节角 qᵢ(°) | 连杆偏移 dᵢ(mm) | 连杆长度 aᵢ(mm) | 连杆扭转角 αᵢ(°) | 关节角偏移 offset(°) |
|---|---|---|---|---|---|
| 1 | q₁(变量) | 540 | 0 | 90 | 90 |
| 2 | q₂(变量) | 0 | -900 | 0 | -90 |
| 3 | q₃(变量) | 0 | -900 | 0 | 0 |
| 4 | q₄(变量) | 500 | 0 | 90 | -90 |
| 5 | q₅(变量) | 345 | 0 | -90 | 0 |
| 6 | q₆(变量) | 175 | 0 | 0 | 0 |
注意事项:
注:a₂和a₃为负值,是因为x轴方向与机械臂连杆延伸方向相反,不影响计算,只需严格按照坐标系定义填写即可。
3. 第三步:计算总变换矩阵与末端位姿
根据参数表,我们先将θᵢ转换为弧度,再依次计算每个连杆的变换矩阵(¹₀T、²₁T...⁶₅T),最后将6个矩阵相乘得到总变换矩阵⁶₀T。
例如,当所有关节角为0°时,代入参数计算得到的总变换矩阵中,前3行第4列即为末端执行器的位置(x,y,z),前3行3列即为末端姿态的旋转矩阵。通过这个结果,我们可以验证建模的正确性(比如零位时末端位置是否与机械臂物理结构一致)。
四、代码实现:用Python验证D-H建模结果
光有理论不够,我们用Python结合NumPy实现D-H建模与正运动学求解,同时加入Matplotlib可视化,直观看到机械臂姿态。
1. 依赖安装
首先安装必要的库(矩阵运算+3D可视化):
python
pip install numpy matplotlib2. 完整代码(含可视化)
python
import numpy as np
import math
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
# ====================== 解决Matplotlib中文显示问题 ======================
plt.rcParams["font.family"] = ["SimHei", "PingFang SC", "WenQuanYi Micro Hei", "DejaVu Sans"]
plt.rcParams['axes.unicode_minus'] = False
mpl.rcParams['font.sans-serif'] = plt.rcParams["font.family"]
# 角度转弧度
def deg2rad(deg):
return deg * math.pi / 180
# 弧度转角度
def rad2deg(rad):
return rad * 180 / math.pi
# 计算单个连杆的D-H变换矩阵(标准D-H)
def dh_transform(theta, d, a, alpha):
T = np.array([
[math.cos(theta), -math.sin(theta) * math.cos(alpha), math.sin(theta) * math.sin(alpha), a * math.cos(theta)],
[math.sin(theta), math.cos(theta) * math.cos(alpha), -math.cos(theta) * math.sin(alpha), a * math.sin(theta)],
[0, math.sin(alpha), math.cos(alpha), d],
[0, 0, 0, 1]
])
return T
# 机械臂正运动学求解(含offset)
def your_arm_forward_kinematics(joint_angles):
"""
参数:
joint_angles: 列表,6个关节角(弧度)[q1, q2, q3, q4, q5, q6]
返回:
T_total: 末端总变换矩阵
joint_positions: 各关节(0-6)的坐标列表
end_rotation: 末端旋转矩阵
"""
# 提取关节角(叠加offset)
q1, q2, q3, q4, q5, q6 = joint_angles
offset = [math.pi / 2, -math.pi / 2, 0, -math.pi / 2, 0, 0] # 关节角偏移
theta1 = q1 + offset[0]
theta2 = q2 + offset[1]
theta3 = q3 + offset[2]
theta4 = q4 + offset[3]
theta5 = q5 + offset[4]
theta6 = q6 + offset[5]
# 机械臂D-H参数(根据你的参数表定义)
d = [540, 0, 0, 500, 345, 175] # 连杆偏移d_i
a = [0, -900, -900, 0, 0, 0] # 连杆长度a_i
alpha = [math.pi / 2, 0, 0, math.pi / 2, -math.pi / 2, 0] # 连杆扭转角α_i
# 计算各连杆变换矩阵
T1 = dh_transform(theta1, d[0], a[0], alpha[0])
T2 = dh_transform(theta2, d[1], a[1], alpha[1])
T3 = dh_transform(theta3, d[2], a[2], alpha[2])
T4 = dh_transform(theta4, d[3], a[3], alpha[3])
T5 = dh_transform(theta5, d[4], a[4], alpha[4])
T6 = dh_transform(theta6, d[5], a[5], alpha[5])
# 各关节相对于基坐标系的变换矩阵
T0_0 = np.eye(4) # 基坐标系
T0_1 = T0_0 @ T1
T0_2 = T0_1 @ T2
T0_3 = T0_2 @ T3
T0_4 = T0_3 @ T4
T0_5 = T0_4 @ T5
T0_6 = T0_5 @ T6 # 末端坐标系
# 提取各关节位置(x,y,z)
joint_positions = [
T0_0[:3, 3], T0_1[:3, 3], T0_2[:3, 3],
T0_3[:3, 3], T0_4[:3, 3], T0_5[:3, 3], T0_6[:3, 3]
]
return T0_6, joint_positions, T0_6[:3, :3]
# 机械臂3D可视化函数
def visualize_your_arm(joint_angles, title="六轴机械臂正运动学可视化"):
# 获取关节位置
T_total, joint_positions, end_rot = your_arm_forward_kinematics(joint_angles)
x = [pos[0] for pos in joint_positions]
y = [pos[1] for pos in joint_positions]
z = [pos[2] for pos in joint_positions]
# 创建3D绘图
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 绘制连杆、关节、末端
ax.plot(x, y, z, 'b-', linewidth=3, label='机械臂连杆')
ax.scatter(x, y, z, c='r', s=100, label='关节', marker='o')
ax.scatter(x[-1], y[-1], z[-1], c='red', s=300, label='末端执行器', marker='*')
# 坐标轴与标题(中文)
ax.set_xlabel('X轴 (mm)', fontsize=12)
ax.set_ylabel('Y轴 (mm)', fontsize=12)
ax.set_zlabel('Z轴 (mm)', fontsize=12)
ax.set_title(title, fontsize=14, fontweight='bold')
ax.legend(loc='upper left', fontsize=10)
# 调整坐标轴范围(适配机械臂尺寸)
ax.set_xlim([-2000, 2000])
ax.set_ylim([-2000, 2000])
ax.set_zlim([0, 2000])
# 打印末端位姿
print("=" * 60)
print("机械臂末端位姿信息:")
print(f"末端位置 (x, y, z):({x[-1]:.2f}, {y[-1]:.2f}, {z[-1]:.2f}) 毫米")
print("末端旋转矩阵:")
print(np.round(end_rot, 3))
# 旋转矩阵转欧拉角(RPY)
def rot2euler(rot):
sy = math.sqrt(rot[0, 0] ** 2 + rot[1, 0] ** 2)
singular = sy < 1e-6
if not singular:
roll = math.atan2(rot[2, 1], rot[2, 2])
pitch = math.atan2(-rot[2, 0], sy)
yaw = math.atan2(rot[1, 0], rot[0, 0])
else:
roll = math.atan2(-rot[1, 2], rot[1, 1])
pitch = math.atan2(-rot[2, 0], sy)
yaw = 0
return [rad2deg(roll), rad2deg(pitch), rad2deg(yaw)]
rpy = rot2euler(end_rot)
print(f"末端姿态(横滚角Roll, 俯仰角Pitch, 偏航角Yaw):({rpy[0]:.2f}, {rpy[1]:.2f}, {rpy[2]:.2f}) 度")
print("=" * 60)
plt.show()
# 自定义输入关节角(支持角度/弧度输入)
def input_joint_angles():
"""
让用户选择输入模式(角度/弧度),并输入6个关节角,返回弧度制的关节角列表
"""
print("=" * 60)
print("欢迎输入六轴机械臂的关节角!")
# 选择输入模式
while True:
mode = input("请选择输入模式(1=角度,2=弧度):")
if mode in ["1", "2"]:
mode = int(mode)
break
else:
print("输入错误!请输入1或2。")
# 输入6个关节角
joint_angles_input = []
joint_names = ["关节1 (q1)", "关节2 (q2)", "关节3 (q3)", "关节4 (q4)", "关节5 (q5)", "关节6 (q6)"]
for i, name in enumerate(joint_names):
while True:
try:
angle = float(input(f"请输入{name}的角度值:"))
joint_angles_input.append(angle)
break
except ValueError:
print("输入错误!请输入数字(整数/小数均可)。")
# 转换为弧度(如果是角度输入)
if mode == 1:
joint_angles_rad = [deg2rad(angle) for angle in joint_angles_input]
print(f"\n你输入的角度(角度制):{[round(angle, 2) for angle in joint_angles_input]}")
print(f"转换为弧度制:{[round(rad, 4) for rad in joint_angles_rad]}")
else:
joint_angles_rad = joint_angles_input
print(f"\n你输入的角度(弧度制):{[round(rad, 4) for rad in joint_angles_rad]}")
print("=" * 60)
return joint_angles_rad
# 主函数
if __name__ == "__main__":
# 自定义输入关节角
joint_angles = input_joint_angles()
# 可视化机械臂
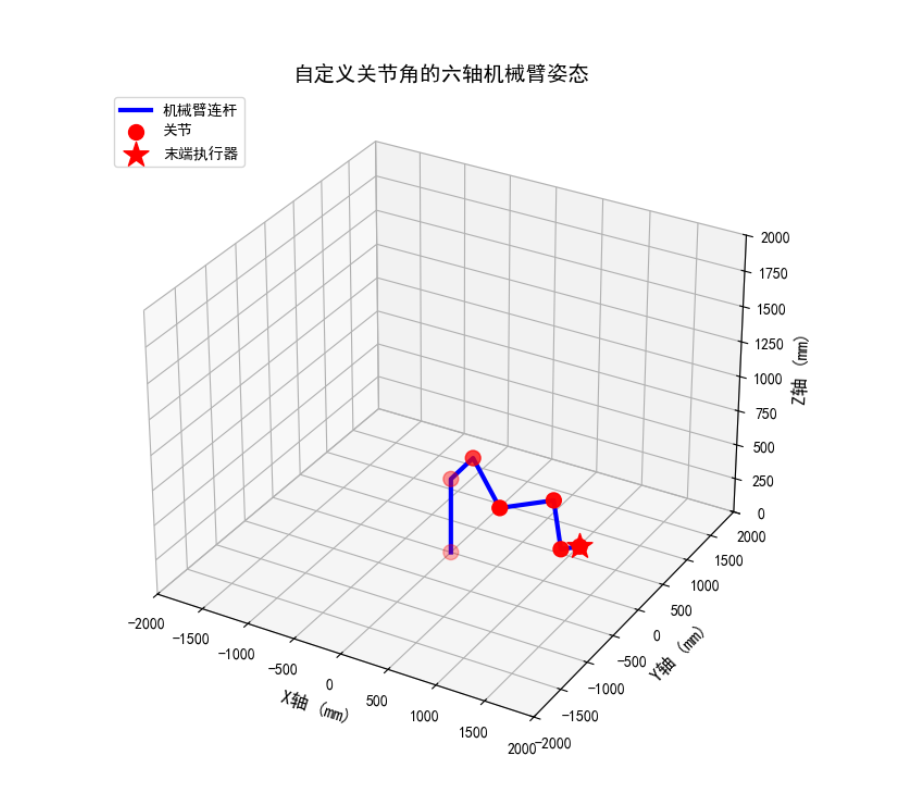
visualize_your_arm(joint_angles, "自定义关节角的六轴机械臂姿态")3. 代码说明与运行效果
代码核心逻辑:用户输入6个关节角(角度制)→ 转换为弧度→ 计算各连杆D-H变换矩阵→ 得到总变换矩阵→ 提取关节位置并可视化。
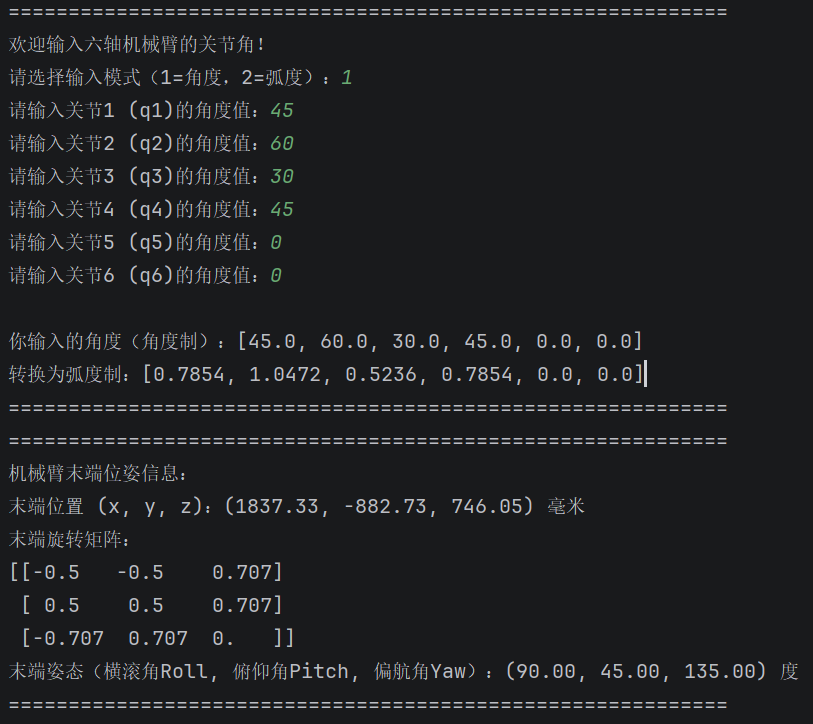
运行后,会弹出3D可视化窗口,蓝色线段为机械臂连杆,红色圆点为关节,红色星号为末端执行器;控制台会输出末端位置和旋转矩阵,方便验证建模结果。