论文发表时间:2019
论文地址:https://arxiv.org/abs/1901.03892
文档: https://dai-lab.github.io/SteganoGAN/
官方代码:(pytorch) https://github.com/DAI-Lab/SteganoGAN
1. Introduction
传统隐写方法在 0.4 bpp 下有效
深度学习可用于识别嵌入位置,或者作为端到端的方案
但深度学习对载体图像大小有限制;或试图在图像中嵌入图像
之前的工作没有探讨能够成功隐藏信息的极限
本文提出一种端到端图像隐写模型SteganoGAN
- 使用dense连接,缓解梯度消失问题,提升性能;
- 在对抗训练框架中使用多个损失函数同时优化 encoder、decoder 和 critic networks;
- 实现任意数据嵌入自然场景载体图片,嵌入率达到 4.4 bpp;

最左边的图是原始载体图片,右侧4幅图分别包含大约每像素1、2、3和4bit的秘密信息,不会产生任何可见伪影
贡献:
- 使用对抗训练解决隐写任务,隐写容量为其他方法10倍;
- 提出评估基于深度学习隐写算法capacity 的方法;
- 通过检测对抗传统隐写分析工具的能力来评估方法;
- 通过检测避免深度学习隐写分析工具的能力来评估方法;
2. Motivation
- 弥补密码学固有缺陷(能够保护信息但无法隐藏信息的存在本身);
- 满足实际场景对隐写需求:高容量(嵌入更多信息)、不可检测(不被发现信息的存在)、无损回复(接收方准确提取信息);
- 解决现有隐写技术的缺陷(嵌入容量低、易被隐写分析工具检测);
3. SteganoGAN
隐写的两个操作:encoding 和 decoding
- endoding : 使用载体图像和二进制消息,创建隐写图像(steganographic image);
- decoding :获取隐写图像,恢复二进制消息
3.1 Notation
- C C C:载体图像
- S S S :隐写图像
以上两者都是RGB格式,有相同分辨率 W × H W\times H W×H - M M M:要写入的二进制消息
M ∈ { 0 , 1 } D × W × H M\in\{0,1\}^{D\times W\times H} M∈{0,1}D×W×H
D D D是相对有效载荷(relative payload)的上限;实际相对有效载荷为 ( 1 − 2 p ) D (1-2p)D (1−2p)D,其中, p ∈ [ 0 , 1 ] p∈[0, 1] p∈[0,1],为error rate.
载体图像 C C C从自然图像分布中采样得到。隐写图像 S S S 通过 learned encoder 生成,即 S = ε ( C , M ) S= {\Large{\varepsilon}} (C,M) S=ε(C,M),秘密消息用 learned decoder 从隐写图像中提取得到,即 M = D ( S ) M=\mathcal D(S) M=D(S)
优化任务: 训练编码器和解码器,最小化损失
- 解码错误率 p p p
- 自然图像和隐写图像分布之间的距离 d i s ( P C , P S ) dis(\mathbb{P}_C, \mathbb{P}_S) dis(PC,PS)。
为了优化解码器和编码器,需要一个评估器 C ( ⋅ ) \mathcal{C}(\cdot) C(⋅) 来度量 d i s ( P C , P S ) dis(\mathbb{P}_C, \mathbb{P}_S) dis(PC,PS)。
定义3种对张量的处理操作:
(1)Cat(拼接):
- 输入:两个张量 X ∈ R D × W × H X \in \mathbb{R}^{D \times W \times H} X∈RD×W×H、 Y ∈ R D ′ × W × H Y \in \mathbb{R}^{D' \times W \times H} Y∈RD′×W×H(宽高相同、深度不同)
- 输出: Φ ∈ R ( D + D ′ ) × W × H \Phi \in \mathbb{R}^{(D+D') \times W \times H} Φ∈R(D+D′)×W×H
- 沿深度轴拼接两个张量,用于合并不同维度的特征
(2) C o n v D → D ′ Conv_{D \rightarrow D'} ConvD→D′ (卷积块)
- 输入: X ∈ R D × W × H X \in \mathbb{R}^{D \times W \times H} X∈RD×W×H
- 输出: Φ ∈ R D ′ × W × H \Phi \in \mathbb{R}^{D' \times W \times H} Φ∈RD′×W×H(宽高不变、深度调整)
- 实现张量深度转换,结构包含:3×3卷积核(步长1、填充"same")+ leaky ReLU 激活函数 + 批归一化;若为网络最后一个块,则省略激活与批归一化。
(3)Mean(自适应均值空间池化)
- 输入: X ∈ R D × W × H X \in \mathbb{R}^{D \times W \times H} X∈RD×W×H
- 输出: R D \mathbb{R}^D RD
- 对张量每个特征图的 W × H W \times H W×H 个空间元素求均值,用于压缩空间维度、提取全局特征。
3.2 Architecture
网络结构如下所示:
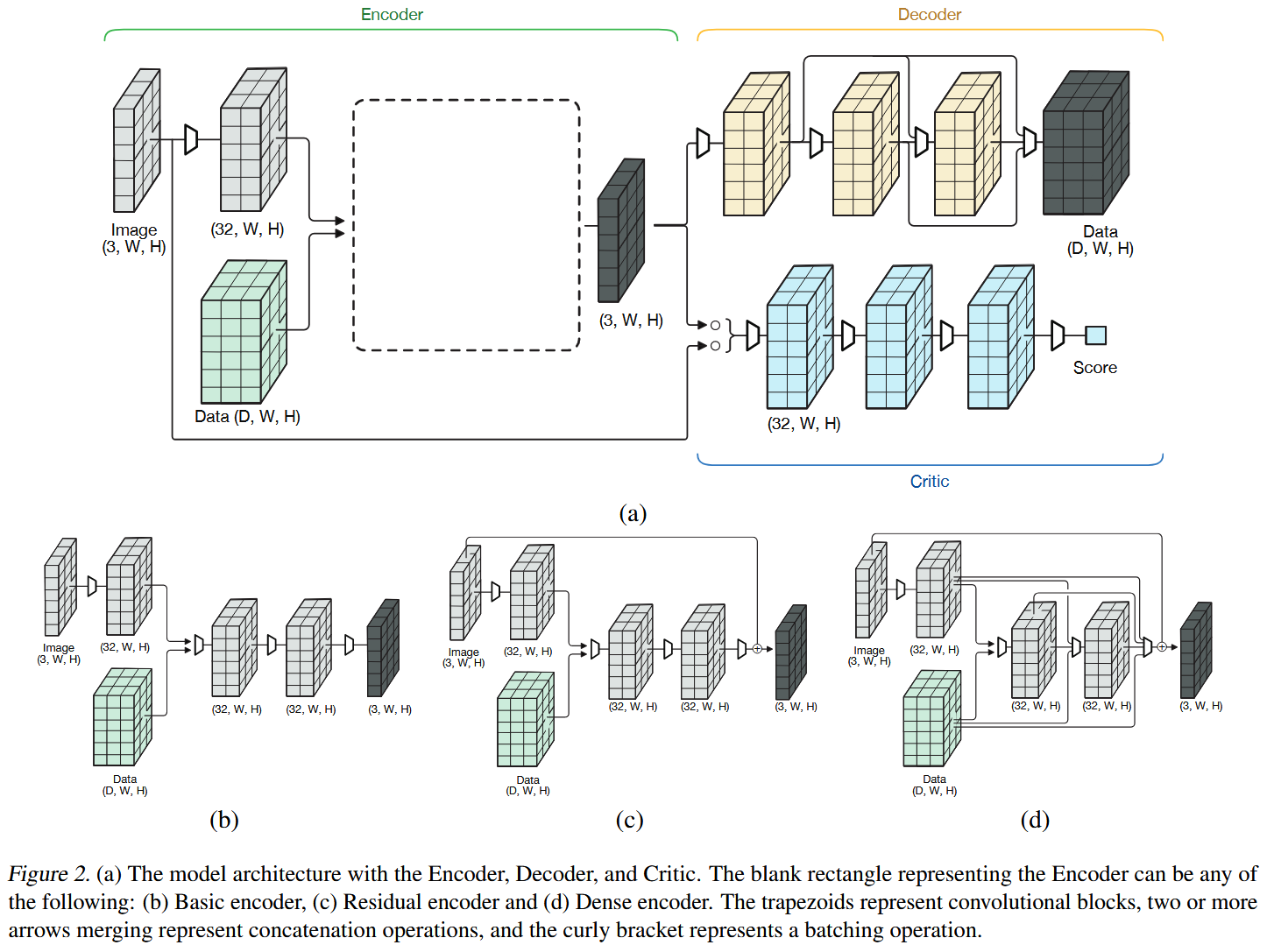
共包含三个模块:
- 编码器:使用载体图像和数据 tensor 或 message,产生隐写图像;
- 解码器:从隐写图像中恢复数据;
- 评估器:评估载体图像和隐写图像的质量;
3.2.1 ENCODER
编码器输入载体图像 C C C 和秘密消息 M M M, M ∈ { 0 , 1 } D × W × H M\in \{0,1\}^{D\times W\times H} M∈{0,1}D×W×H ,其中, D D D 是在每个载体图像像素上试图隐藏的比特数。
论文提出了三种编码器结构,分别是Basic,Residual,Dense,它们最开始都是同样两个步骤
1、对载体图像进行卷积得到张量 a a a
a = C o n v 3 → 32 ( C ) (1) a=Conv_{3\rightarrow32}(C) \tag{1} a=Conv3→32(C)(1)
这里维度从3维转换到32维
2、把 M M M连接到 a a a上,再进行卷积,得到张量 b b b
b = C o n v 32 + D → 32 ( C a t ( a , M ) ) (2) b=Conv_{32+D\rightarrow32}(Cat(a,M)) \tag{2} b=Conv32+D→32(Cat(a,M))(2)
Cat是连接操作
Basic:
对 b b b 进 行两次卷积,生成隐写图像
E ( C , M ) = C o n v 32 → 3 ( C o n v 32 → 32 ( b ) ) (3) \mathcal{E} (C,M)=Conv_{32\rightarrow3}(Conv_{32\rightarrow32}(b)) \tag{3} E(C,M)=Conv32→3(Conv32→32(b))(3)
Residual:
把 C C C(载体图像)加到Basic产生的隐写图像上
E r ( C , M ) = C + E b ( C , M ) (4) \mathcal{E}_r (C,M)=C + \mathcal{E}_b(C,M) \tag{4} Er(C,M)=C+Eb(C,M)(4)
Dense:
采用DenseNet,允许特征重用,缓和梯度消失问题,提升嵌入率
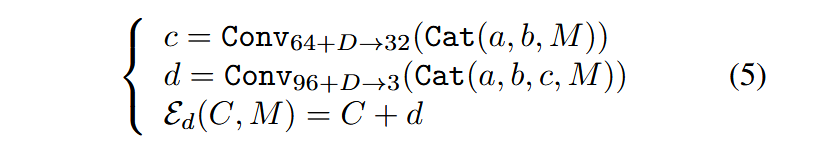
在训练的时候选择这三种编码器其中一个,得到隐写图像(当然,效果最好的是Dense)
最后,每个变体的输出是隐写图像 S = E b , r , d ( C , M ) S = E_{b,r,d} (C,M) S=Eb,r,d(C,M),其分辨率和深度与载体图像 C C C 相同。
3.2.2 DECODER
输入隐写图像,得出秘密消息
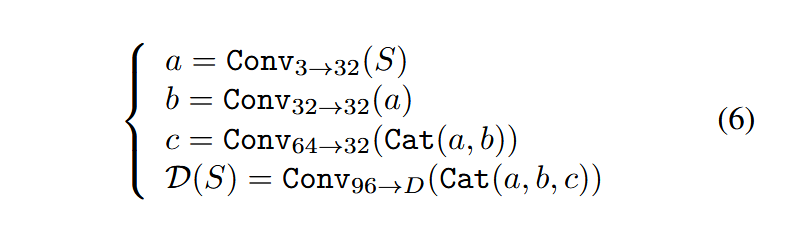
3.2.3 CRITIC
目的:对编码器的性能提供反馈并生成更真实的图像。三个卷积块后接一个输出为1的卷积层,最后生成一个得分,来评估生成图像为隐写图像的概率,采用自适应均值池化
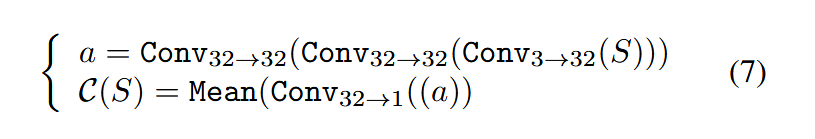
3.3 Training
迭代优化 encoder-decoder 和 critic 网络
1、优化编码-解码网咯,要最优化三个损失
(1)解码正确率:用交叉熵损失来衡量
L d = E X ∼ P C CrossEntropy ( D ( E ( X , M ) ) , M ) (8) \mathcal{L}d = \mathbb{E}{X \sim \mathbb{P}_C} \text{CrossEntropy}\left(\mathcal{D}\left(\mathcal{E}(X,M)\right), M\right) \tag{8} Ld=EX∼PCCrossEntropy(D(E(X,M)),M)(8)
(2)隐写图像和载体图像的相似性:用均方误差来衡量
L s = E X ∼ P C 1 3 × W × H ∥ X − E ( X , M ) ∥ 2 2 (9) \mathcal{L}s = \mathbb{E}{X \sim \mathbb{P}_C} \frac{1}{3 \times W \times H} \left\| X - \mathcal{E}(X,M) \right\|_2^2 \tag{9} Ls=EX∼PC3×W×H1∥X−E(X,M)∥22(9)
(3)隐写图像的真实性:用评估器来衡量
L r = E X ∼ P C C ( E ( X , M ) ) (10) \mathcal{L}r = \mathbb{E}{X \sim \mathbb{P}_C} \ \mathcal{C}\left(\mathcal{E}(X,M)\right) \tag{10} Lr=EX∼PC C(E(X,M))(10)
训练目标是最小化以上三个损失
minimize L d + L s + L r (11) \text{minimize} \quad \mathcal{L}_d + \mathcal{L}_s + \mathcal{L}_r \tag{11} minimizeLd+Ls+Lr(11)
2、优化评估网络,需要最小化 Wasserstein loss
隐写图像和载体图像数据分布之间的差异
L c = E X ∼ P C C ( X ) − E X ∼ P C C ( E ( X , M ) ) \begin{equation} \tag{12} \begin{aligned} \mathcal{L}c &= \mathbb{E}{X \sim \mathbb{P}C}\ \mathcal{C}(X) \\ &\quad - \mathbb{E}{X \sim \mathbb{P}_C} \ \mathcal{C}\left(\mathcal{E}(X,M)\right) \end{aligned} \end{equation} Lc=EX∼PC C(X)−EX∼PC C(E(X,M))(12)
在每次迭代中,对每个载体图像 C C C,都用一个数据张量 M M M 匹配, M M M 是由从伯努利分布中采样得到的, M ∼ Ber ( 0.5 ) M \sim \text{Ber}(0.5) M∼Ber(0.5),由 D × W × H D×W×H D×W×H bit随机序列组成,随着训练进行,生成的隐写图像越来越趋近于真实图像。
预处理中采用标准数据增强处理,包括水平翻转、随机裁剪。
使用Adam优化器,学习率0.0001,梯度标准为0.25,裁剪评估器权重在 [ − 0.1 , 0.1 ] [-0.1,0.1] [−0.1,0.1],训练 32 epoch。
4. Evaluation Metrics
隐写算法从3个维度进行评估:
- 容量(capacity):隐藏的数据量;
- 失真(distortion):载体图像和隐写图像的相似度;
- 保密性(secrecy):避免被隐写分析工具检测的能力;
本文提出了一些评估标准:
1、每像素有效传输比特数RS-BPP(reed solomon bits per pixel)
背景 :
在隐写算法中,单比特解码错误概率为 p p p 时,直接用 "总比特数×( 1 − p 1-p 1−p)" 估算有效载荷是没有意义的---该方法仅能统计正确解码的比特数,无法纠错或识别错误比特。
解决方案:里德-所罗门(Reed-Solomon)纠错码
- 对于长度为 k k k的原始消息,经过编码生成长度为 n n n的消息, n ≥ k n≥k n≥k;
- 最多可纠正 n − k 2 \frac{n-k}{2} 2n−k位的错误比特(Reed & Solomon, 1960)
为了保证错误可纠正,需满足 "错误比特数≤ 可纠正比特数",即
p ⋅ n ≤ n − k 2 (13) p \cdot n \leq \frac{n - k}{2} \tag{13} p⋅n≤2n−k(13)
可推导出有效载荷的比特率为 k n ≤ 1 − 2 p \frac{k}{n} \leq 1-2p nk≤1−2p
最终 Reed-Solomon bits-per-pixel (RSBPP) 定义为:尝试隐藏的每像素比特数× k n \frac{k}{n} nk,代表每像素有效传输的实际比特数,可与传统隐写技术的比特率直接对比。
2、峰值信噪比(PSNR)
通过测量图像失真来评估隐写的质量。(越大越好)
给定两幅大小为 ( W , H ) (W,H) (W,H) 的图像 X X X 与 Y Y Y ,和一个表示每个像素中可能存在的最大差异的缩放因子 s c sc sc 。则PSNR可以由均方误差MSE给出
MSE = 1 W H ∑ i = 1 W ∑ j = 1 H ( X i , j − Y i , j ) 2 (14) \text{MSE} = \frac{1}{WH} \sum_{i=1}^{W} \sum_{j=1}^{H} (X_{i,j} - Y_{i,j})^2 \tag{14} MSE=WH1i=1∑Wj=1∑H(Xi,j−Yi,j)2(14)
PSNR = 20 ⋅ log 10 ( s c ) − 10 ⋅ log 10 ( MSE ) (15) \text{PSNR} = 20 \cdot \log_{10}(sc) - 10 \cdot \log_{10}(\text{MSE}) \tag{15} PSNR=20⋅log10(sc)−10⋅log10(MSE)(15)
MSE越小,则PSNR越大;所以PSNR越大,代表着图像质量越好。一般来说:
- PSNR高于40dB说明图像质量极好(即非常接近原始图像);
- 在30---40dB通常表示图像质量是好的(即失真可以察觉但可以接受);
- 在20---30dB说明图像质量差;
- 低于20dB图像不可接受。
但PSNR可能不太适合用于比较不同隐写算法,所以引入结构相似性指数(SSIM)
结构相似度指数(SSIM)
同样用于测量图像质量
对于给定图像 X X X 和 Y Y Y ,SSIM可用均值 μ X \mu_X μX , μ Y \mu_Y μY,方差 σ X 2 \sigma_X^2 σX2、 σ Y 2 \sigma_Y^2 σY2 和协方差 σ X Y \sigma_{XY} σXY 来计算
SSIM = ( 2 μ X μ Y + k 1 R ) ( 2 σ X Y + k 2 R ) ( μ X 2 + μ Y 2 + k 1 R ) ( σ X 2 + σ Y 2 + k 2 R ) (16) \text{SSIM} = \frac{(2\mu_X \mu_Y + k_1 R)(2\sigma_{XY} + k_2 R)}{(\mu_X^2 + \mu_Y^2 + k_1 R)(\sigma_X^2 + \sigma_Y^2 + k_2 R)} \tag{16} SSIM=(μX2+μY2+k1R)(σX2+σY2+k2R)(2μXμY+k1R)(2σXY+k2R)(16)
k 1 = 0.01 k_1 = 0.01 k1=0.01, k 2 = 0.03 k_2 = 0.03 k2=0.03, 返回值范围在 [ − 1.0 , 1.0 ] [−1.0, 1.0] [−1.0,1.0] ,1.0表示内容相同
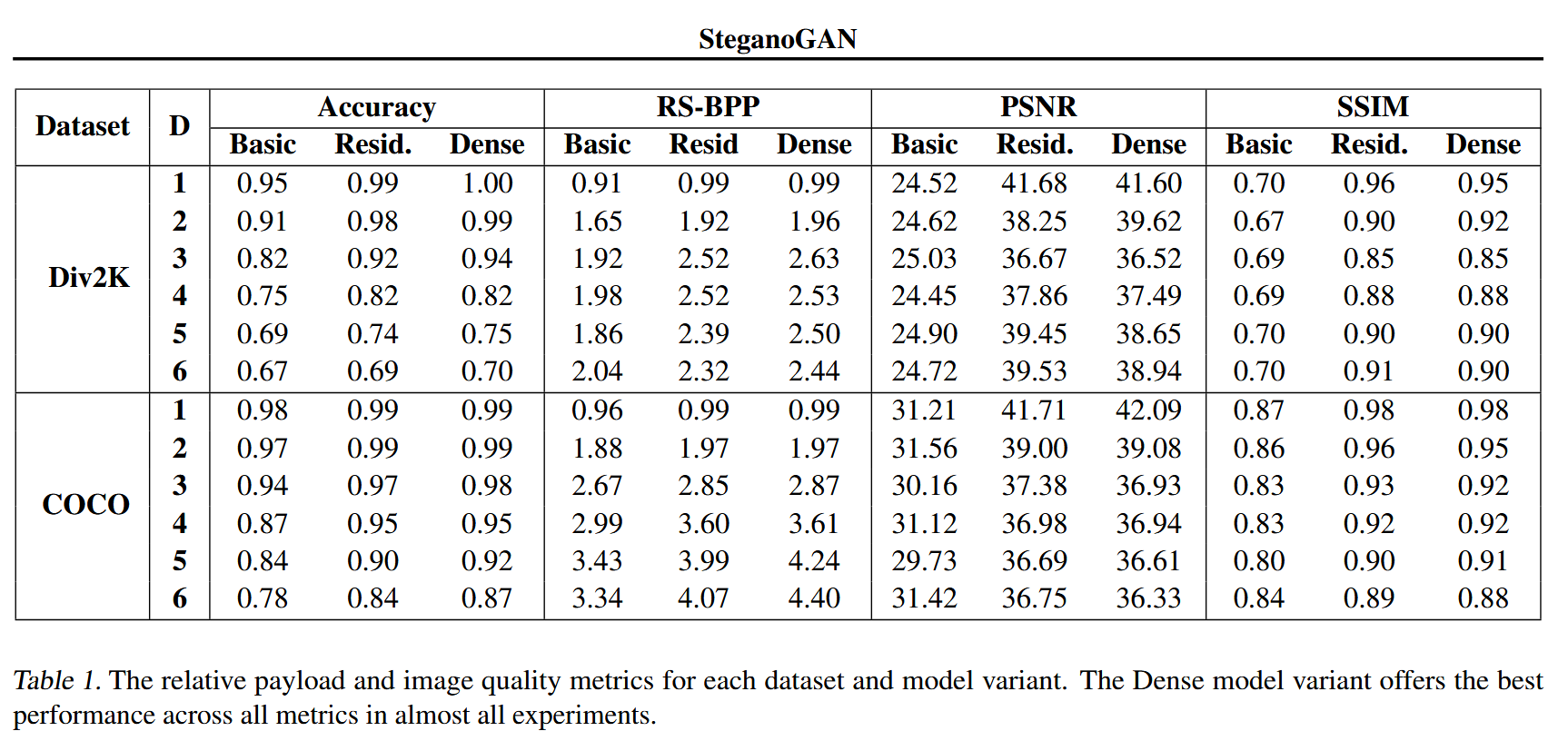
5. Results and Analysis
- 使用Div2k和 COCO 2014训练模型,采用官方默认的训练/测试划分;
- 测试3种模型,6种数据深度 D D D;
6. Detecting Steganographic Images
隐写算法的关键指标之一是规避隐写分析工具检测的能力
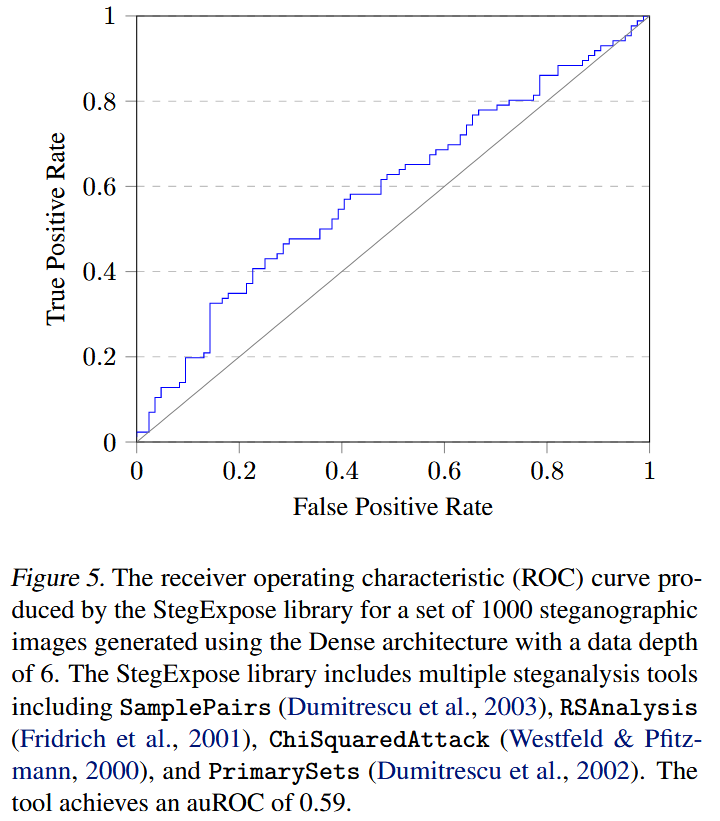
6.1. Statistical Steganalysis
- 隐写分析工具:StegExpose
- auROC为0.59
6.2 Neural Steganalysis
-
方法:Ye et al. (2017) 的深度学习隐写分析模型
-
模拟 "检测方已知隐写算法(STEGANOGAN)但未知具体模型权重" 的场景:
- 用不同随机种子训练 N N N个密集模型;
- 每个模型生成 1000 张隐写图像;
- 保留第 N N N个模型的图像作为测试集,用前1到 N − 1 N-1 N−1个模型的图像训练检测模型;
- 重复实验 3 次,报告平均 auROC;
-
核心问题:检测方仅知隐写算法(不知具体模型权重)时,能否检测出本文模型生成的隐写图像?
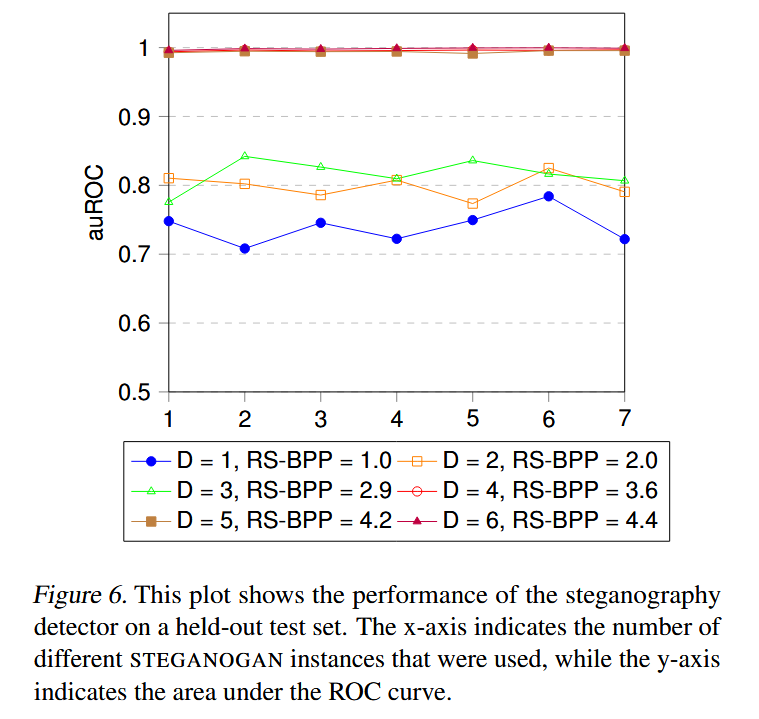
Figure 6展示了不同有效载荷(RS-BPP)和训练集规模下的检测器 auROC:
- 有效载荷的影响:每像素编码比特数(RS-BPP)越高,检测器的 auROC 越高(检测性能越强);
- 训练模型数量的影响:增加训练用的 STEGANOGAN 模型数量,auROC 无明显趋势 ------ 说明 "仅知隐写算法、不知具体模型参数" 的检测方,难以构建有效的检测模型。
与现有隐写技术的对比,在 "检测错误率 20%" 的固定条件下,对比 STEGANOGAN 与 3 种经典隐写算法的最大有效载荷:WOW为0.3 bpp,S-UNIWARD 为0.4 bpp,HILL为0.5 bpp。
7. 相关工作
传统隐写方法:传统方法以 "手工设计特征 + 最小化失真" 为核心思路
- HUGO
- JSteg
基于深度学习的隐写方法:
- Hayes & Danezis(2017)
- 仅支持固定尺寸图像,灵活性差;
- payload 超过 0.4 bpp 时,图像质量严重下降
- Zhu et al.(2018)
- 高 payload 下内存开销大
SteganoGAN 创新点:
- 支持任意尺寸载体图像和任意二进制数据嵌入,而非局限于 "图像嵌入图像";
- 采用Dense Connection和多损失函数优化,实现 4.4 bpp 的 state-of-the-art payload;
- 提出 RS-BPP metric,解决了深度学习方法与传统方法的 "payload 对比难题"。
缺点:鲁棒性较差,如JPEG压缩、截图、调整大小或旋转,将使隐藏的数据无法提取。无法保证完全提取秘密信息。
参考 :
1、【论文阅读】SteganoGAN: High Capacity Image Steganography with GANs
2、基于GAN的高容量隐写术:SteganoGAN: High Capacity Image Steganography with GANs