matlab推导QPR离散公式并验证

轻微的风格艾丝凡2025-12-25 11:37

目录

[1. 功能概述](#1. 功能概述)

[2. 依赖环境](#2. 依赖环境)

[3. 核心参数说明](#3. 核心参数说明)

[4. 关键输出说明](#4. 关键输出说明)

[5. 核心算法逻辑](#5. 核心算法逻辑)

[6. 使用方法](#6. 使用方法)

[7. 注意事项](#7. 注意事项)

[8. 典型应用场景](#8. 典型应用场景)

9.代码

1. 功能概述

本脚本实现准谐振控制器（QPR） 的离散化设计，核心包含两大模块：

  • 符号推导：基于 Tustin 变换推导 QPR 离散化通用公式，代入数值得到离散系数；
  • 官方验证：通过 MATLAB 内置c2d函数（数值传递函数输入）验证符号推导结果，输出频率特性对比及工程化差分方程。
2. 依赖环境
  • MATLAB 版本：R2014b 及以上（兼容所有新版本）；
  • 必备工具箱：
    • Symbolic Math Toolbox（符号推导）；
    • Control System Toolbox（tf/c2d函数）。
3. 核心参数说明
参数名 含义 默认值 单位
Kr_val 谐振系数 100 -
f0_val 谐振频率 50 Hz
wc_val 截止角频率 10 rad/s
Ts_val 采样周期 1e-4 s（100μs）
4. 关键输出说明
输出模块 核心内容 用途
符号推导通用公式 z²/z¹/z⁰阶的分子 / 分母符号系数 理论分析、参数化设计
数值离散系数 代入参数后的具体系数值 代码实现、硬件部署
c2d 验证结果 官方工具离散化系数 验证符号推导正确性
频率特性图 连续 / 离散 QPR 的波特图 频域性能验证
差分方程 数值化的递推公式 嵌入式代码（C/MCU）实现
5. 核心算法逻辑
  1. 连续 QPR 模型：Gcont(s)=s2+2ωcs+ω022Krs；
  2. Tustin 变换：s=Ts2⋅z+1z−1，代入连续模型后通分、展开；
  3. 系数提取：遍历多项式幂次，精准提取 z²/z¹/z⁰阶系数（避免顺序错误）；
  4. 归一化 ：分母首项归一化为 1，与c2d输出格式对齐；
  5. 验证 ：对比符号推导与c2d系数，计算最大误差；
  6. 工程化：将离散传递函数转换为差分方程，直接用于实时控制。
6. 使用方法
  1. 保存脚本为QPR.m，确保 MATLAB 加载所需工具箱；
  2. （可选）修改参数（如f0_val/Ts_val）适配具体应用场景；
  3. 直接运行脚本，按命令行输出和图形化结果分析：
    • 若「验证通过」，则符号推导系数可直接使用；
    • 频率特性图需确认 50Hz 处增益与连续 QPR 一致；
    • 差分方程系数可复制到嵌入式代码中实现 QPR 控制。
7. 注意事项
  1. 若提示coeffs未定义：确认安装 Symbolic Math Toolbox；
  2. 若系数对比误差大于 1e-8：检查参数赋值（如ω0=2πf0）或采样周期单位；
  3. 工程实现时：差分方程需注意变量延迟（e (k-1)/u (k-1)）的缓存与更新。
8. 典型应用场景
  • 并网逆变器谐波抑制；
  • 有源电力滤波器（APF）；
  • 不间断电源（UPS）电压 / 电流控制；
  • 其他需要谐振点无静差跟踪的场合。
9.代码
Matlab 复制代码 
%% QPR离散化：符号推导+官方c2d对比（无Kp）
clear; clc; close all;

% 符号变量定义
syms Kr wc w0 Ts z s;

% 连续QPR传递函数
G_cont = (2*Kr*s) / (s^2 + 2*wc*s + w0^2);
disp('\n1. 连续QPR传递函数（符号）：');
pretty(G_cont);

% Tustin变换映射
s_tustin = (2/Ts) * (z - 1)/(z + 1);
disp('\n2. Tustin变换：s → z映射：');
pretty(s_tustin);

% 代入并化简
G_z_unreduced = subs(G_cont, s, s_tustin);
[num_unreduced, den_unreduced] = numden(G_z_unreduced);
num_expanded = expand(num_unreduced);
den_expanded = expand(den_unreduced);

% 提取分子系数（z²/z¹/z⁰）
[num_coeffs, num_powers] = coeffs(num_expanded, z);
num_z2 = 0; num_z1 = 0; num_z0 = 0;
for i = 1:length(num_powers)
    power = num_powers(i);
    if power == z^2
        num_z2 = num_coeffs(i);
    elseif power == z^1
        num_z1 = num_coeffs(i);
    elseif power == z^0
        num_z0 = num_coeffs(i);
    end
end
num_coeff_z_sym = [num_z2, num_z1, num_z0];

% 提取分母系数（z²/z¹/z⁰）
[den_coeffs, den_powers] = coeffs(den_expanded, z);
den_z2 = 0; den_z1 = 0; den_z0 = 0;
for i = 1:length(den_powers)
    power = den_powers(i);
    if power == z^2
        den_z2 = den_coeffs(i);
    elseif power == z^1
        den_z1 = den_coeffs(i);
    elseif power == z^0
        den_z0 = den_coeffs(i);
    end
end
den_coeff_z_sym = [den_z2, den_z1, den_z0];

% 输出符号系数
disp('\n3. 符号推导：离散系数通用公式（z²/z¹/z⁰）：');
disp('分子系数（a2*z² + a1*z + a0）：');
fprintf('a2 = '); pretty(num_coeff_z_sym(1));
fprintf('a1 = '); pretty(num_coeff_z_sym(2));
fprintf('a0 = '); pretty(num_coeff_z_sym(3));
disp('分母系数（b2*z² + b1*z + b0）：');
fprintf('b2 = '); pretty(den_coeff_z_sym(1));
fprintf('b1 = '); pretty(den_coeff_z_sym(2));
fprintf('b0 = '); pretty(den_coeff_z_sym(3));

% 代入数值
Kr_val = 100;
f0_val = 50;
wc_val = 10;
w0_val = 2*pi*f0_val;
Ts_val = 1e-4;
sym_subs = {Kr, wc, w0, Ts};
val_subs = {Kr_val, wc_val, w0_val, Ts_val};
num_z_sym_num = double(subs(num_coeff_z_sym, sym_subs, val_subs));
den_z_sym_num = double(subs(den_coeff_z_sym, sym_subs, val_subs));

% 分母归一化
den_lead_sym = den_z_sym_num(1);
if den_lead_sym ~= 0
    num_z_sym_num = num_z_sym_num / den_lead_sym;
    den_z_sym_num = den_z_sym_num / den_lead_sym;
end

% 输出符号推导数值结果
disp('\n4. 符号推导→数值离散系数：');
fprintf('分子（z²/z¹/z⁰）：a2=%.6f, a1=%.6f, a0=%.6f\n', num_z_sym_num(1), num_z_sym_num(2), num_z_sym_num(3));
fprintf('分母（z²/z¹/z⁰）：b2=%.6f, b1=%.6f, b0=%.6f\n', den_z_sym_num(1), den_z_sym_num(2), den_z_sym_num(3));

% 官方c2d（数值num/den）
num_cont = [0, 2*Kr_val, 0];
den_cont = [1, 2*wc_val, w0_val^2];
G_cont_tf = tf(num_cont, den_cont);
G_z_tf = c2d(G_cont_tf, Ts_val, 'tustin');

% 提取c2d系数
num_c2d = [];
den_c2d = [];
if iscell(G_z_tf.Numerator)
    num_c2d = G_z_tf.Numerator{1};
    den_c2d = G_z_tf.Denominator{1};
else
    num_c2d = num(G_z_tf);
    den_c2d = den(G_z_tf);
end

% 补全c2d系数
num_c2d_num = zeros(1, 3);
den_c2d_num = zeros(1, 3);
num_c2d_len = length(num_c2d);
den_c2d_len = length(den_c2d);
if num_c2d_len == 1
    num_c2d_num(3) = num_c2d(1);
elseif num_c2d_len == 2
    num_c2d_num(2:3) = num_c2d(1:2);
elseif num_c2d_len >= 3
    num_c2d_num(1:3) = num_c2d(1:3);
end
if den_c2d_len == 1
    den_c2d_num(3) = den_c2d(1);
elseif den_c2d_len == 2
    den_c2d_num(2:3) = den_c2d(1:2);
elseif den_c2d_len >= 3
    den_c2d_num(1:3) = den_c2d(1:3);
end

% c2d系数归一化
den_lead_c2d = den_c2d_num(1);
if den_lead_c2d ~= 0
    num_c2d_num = num_c2d_num / den_lead_c2d;
    den_c2d_num = den_c2d_num / den_lead_c2d;
end

% 输出c2d数值结果
disp('\n5. 官方c2d离散系数：');
fprintf('分子（z²/z¹/z⁰）：a2=%.6f, a1=%.6f, a0=%.6f\n', num_c2d_num(1), num_c2d_num(2), num_c2d_num(3));
fprintf('分母（z²/z¹/z⁰）：b2=%.6f, b1=%.6f, b0=%.6f\n', den_c2d_num(1), den_c2d_num(2), den_c2d_num(3));

% 结果对比
disp('\n6. 符号推导 vs 官方c2d：');
fprintf('分子系数：\n  符号推导：[%.6f, %.6f, %.6f]\n  官方c2d：[%.6f, %.6f, %.6f]\n', ...
    num_z_sym_num(1), num_z_sym_num(2), num_z_sym_num(3), num_c2d_num(1), num_c2d_num(2), num_c2d_num(3));
fprintf('分母系数：\n  符号推导：[%.6f, %.6f, %.6f]\n  官方c2d：[%.6f, %.6f, %.6f]\n', ...
    den_z_sym_num(1), den_z_sym_num(2), den_z_sym_num(3), den_c2d_num(1), den_c2d_num(2), den_c2d_num(3));

% 误差计算
num_error = max(abs(num_z_sym_num - num_c2d_num));
den_error = max(abs(den_z_sym_num - den_c2d_num));
fprintf('最大误差：\n  分子：%.8f\n  分母：%.8f\n', num_error, den_error);
if num_error < 1e-8 && den_error < 1e-8
    fprintf('✅ 验证通过：结果完全一致\n');
else
    fprintf('⚠️  存在误差：需检查参数或推导\n');
end

% 频率特性验证
freq = linspace(10, 100, 1000);
omega = 2 * pi * freq;
mag_cont = zeros(size(freq));
mag_sym = zeros(size(freq));
mag_c2d = zeros(size(freq));
for i = 1:length(freq)
    s_j = 1j * omega(i);
    G_cont = (num_cont(1)*s_j^2 + num_cont(2)*s_j + num_cont(3)) / (den_cont(1)*s_j^2 + den_cont(2)*s_j + den_cont(3));
    mag_cont(i) = 20 * log10(abs(G_cont));
    
    z_j = exp(1j * omega(i) * Ts_val);
    G_sym = (num_z_sym_num(1)*z_j^2 + num_z_sym_num(2)*z_j + num_z_sym_num(3)) / (den_z_sym_num(1)*z_j^2 + den_z_sym_num(2)*z_j + den_z_sym_num(3));
    mag_sym(i) = 20 * log10(abs(G_sym));
    
    G_c2d = (num_c2d_num(1)*z_j^2 + num_c2d_num(2)*z_j + num_c2d_num(3)) / (den_c2d_num(1)*z_j^2 + den_c2d_num(2)*z_j + den_c2d_num(3));
    mag_c2d(i) = 20 * log10(abs(G_c2d));
end

% 绘制波特图
figure('Color','white','Position',[100,100,1000,600]);
plot(freq, mag_cont, 'b-', 'LineWidth',1.5); hold on;
plot(freq, mag_sym, 'r--', 'LineWidth',1.5); hold on;
plot(freq, mag_c2d, 'g:', 'LineWidth',1.5); hold off;
grid on;
legend('连续QPR','符号推导离散QPR','官方c2d离散QPR','Location','best');
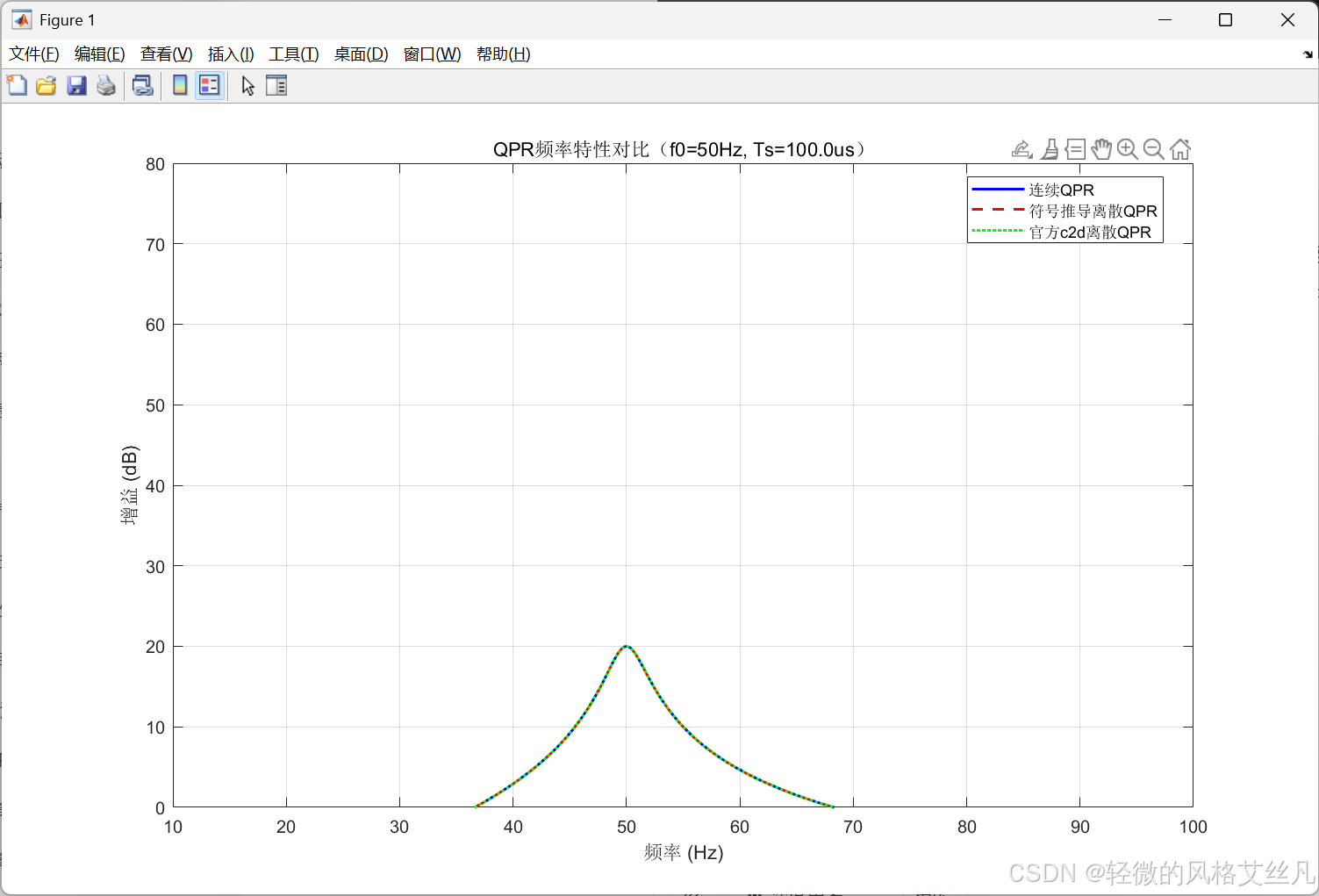
title(sprintf('QPR频率特性对比（f0=%dHz, Ts=%.1fus）', f0_val, Ts_val*1e6), 'FontSize',12);
xlabel('频率 (Hz)'); ylabel('增益 (dB)');
xlim([10, 100]); ylim([0, 80]);
set(gca, 'FontSize',10);

% 50Hz增益
idx_50 = find(freq>=50, 1);
if ~isempty(idx_50)
    fprintf('\n7. 50Hz处增益：\n  连续：%.2fdB\n  符号推导：%.2fdB\n  官方c2d：%.2fdB\n', ...
        mag_cont(idx_50), mag_sym(idx_50), mag_c2d(idx_50));
end

% 差分方程
a2 = num_z_sym_num(1); a1 = num_z_sym_num(2); a0 = num_z_sym_num(3);
b1 = den_z_sym_num(2); b0 = den_z_sym_num(3);
fprintf('\n8. 工程化差分方程：\n');
fprintf('u(k) = %.6f·e(k) + %.6f·e(k-1) + %.6f·e(k-2) - %.6f·u(k-1) - %.6f·u(k-2)\n', ...
    a2, a1, a0, b1, b0);
10.运行结果
  1. 连续QPR传递函数（符号）：

2 Kr s

2 2

s + wc s 2 + w0

\n2. Tustin变换：s → z映射：

2 (z - 1)

Ts (z + 1)

\n3. 符号推导：离散系数通用公式（z²/z¹/z⁰）：

分子系数（a2*z² + a1*z + a0）：

a2 = 4 Kr Ts

a1 = 0

a0 = -4 Kr Ts

分母系数（b2*z² + b1*z + b0）：

b2 = 2 2

Ts w0 + wc Ts 4 + 4

b1 = 2 2

2 Ts w0 - 8

b0 = 2 2

Ts w0 - wc Ts 4 + 4

\n4. 符号推导→数值离散系数：

分子（z²/z¹/z⁰）：a2=0.009988, a1=0.000000, a0=-0.009988

分母（z²/z¹/z⁰）：b2=1.000000, b1=-1.997017, b0=0.998002

\n5. 官方c2d离散系数：

分子（z²/z¹/z⁰）：a2=0.009988, a1=0.000000, a0=-0.009988

分母（z²/z¹/z⁰）：b2=1.000000, b1=-1.997017, b0=0.998002

\n6. 符号推导 vs 官方c2d：

分子系数：

符号推导：[0.009988, 0.000000, -0.009988]

官方c2d：[0.009988, 0.000000, -0.009988]

分母系数：

符号推导：[1.000000, -1.997017, 0.998002]

官方c2d：[1.000000, -1.997017, 0.998002]

最大误差：

分子：0.00000000

分母：0.00000000

✅ 验证通过：结果完全一致

  1. 50Hz处增益：

连续：20.00dB

符号推导：20.00dB

官方c2d：20.00dB

  1. 工程化差分方程：

u(k) = 0.009988·e(k) + 0.000000·e(k-1) + -0.009988·e(k-2) - -1.997017·u(k-1) - 0.998002·u(k-2)

结论

公式为

其中

推导可见推导

相关推荐
ytttr8732 小时前
MATLAB基于CNN的图像超分辨率重建实现
matlab·cnn·超分辨率重建
岁岁的O泡奶2 小时前
NSSCTF_crypto_[SWPU 2020]happy
经验分享·python·算法·密码学
EchoL、3 小时前
【论文阅读】SteganoGAN：High Capacity Image Steganography with GANs
论文阅读·人工智能·笔记·算法
CoovallyAIHub3 小时前
深度学习驱动的视频异常检测（VAD），AI如何让监控更智能？
深度学习·算法·计算机视觉
于樱花森上飞舞3 小时前
【多线程】常见的锁策略与锁
java·开发语言·算法·java-ee
HUST3 小时前
C 语言 第八讲：VS实用调试技巧
运维·c语言·开发语言·数据结构·算法·c#
历程里程碑3 小时前
LeetCode128：哈希集合巧解最长连续序列
开发语言·数据结构·c++·算法·leetcode·哈希算法·散列表
@淡 定3 小时前
Hash 索引与 B+树索引的区别与适用场景
b树·算法·哈希算法
Tzarevich3 小时前
算法效率的核心：时间复杂度与空间复杂度
javascript·算法
热门推荐
01GitHub 镜像站点02从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击033D 圣诞树网页代码04UV安装并设置国内源05Gemini3 生成的基于手势控制3D粒子圣诞树06Linux下V2Ray安装配置指南07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题09GLM-4.7 vs MiniMax-M2.1：代码工程理解10Labelme从安装到标注：零基础完整指南