【计算机视觉】07_几何变换

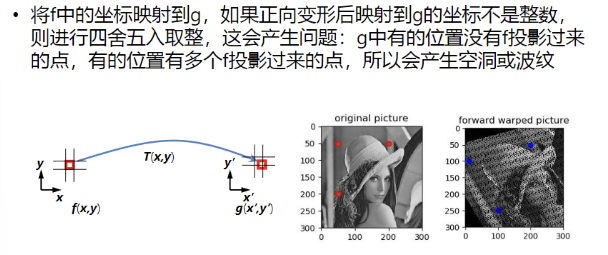
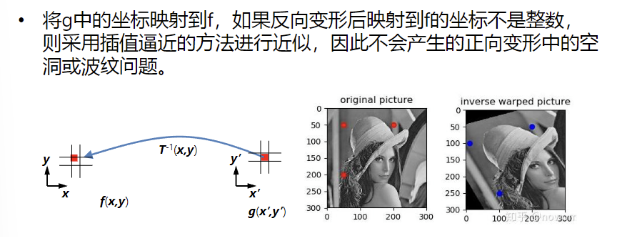
1. 图像形变与几何变换类型

A. 图像形变 (Image Warping)

与改变像素值的图像滤波不同，图像形变是改变图像的空间坐标。

它定义了源图像像素 (x,y)(x, y)(x,y) 如何映射到目标图像 (x′,y′)(x', y')(x′,y′)。

B. 变换的层级

课件介绍了几种从简单到复杂的 2D 平面变换,：

平移 (Translation)：仅移动位置。
刚体变换 (Rigid) ：平移 + 旋转。
相似变换 (Similarity) ：刚体 + 均匀缩放。
仿射变换 (Affine)：

相比刚体变换，它还会改变目标的形状，但保持平直性（平行线变换后依然平行）。

投影变换 / 单应性变换 (Projective / Homography)：

这是最通用的线性变换。
直观含义 ：用无镜头畸变的相机从不同位置拍摄同一平面物体的图像之间存在单应性。
它是图像拼接（全景图）的核心模型。
自由度 ：单应性矩阵是一个 3×33 \times 33×3 的矩阵，但只有 8 个自由度 （通常归一化使得 h33=1h_{33}=1h33=1 或模为1）。

2. 如何估计变换矩阵？（核心：RANSAC）

我们通常通过匹配的特征点对来计算单应性矩阵 HHH。但上一讲提到，特征匹配存在误匹配（Outliers）。如果直接用最小二乘法求解，一个错误的匹配就会破坏整个结果。

因此，我们需要使用 RANSAC (Random Sample Consensus，随机抽样一致算法)。

A. RANSAC 算法流程

RANSAC 是一种迭代算法，其核心思想是："好的匹配都是相似的，坏的匹配各有各的坏法"。

随机采样 ：随机选择最少数量的数据点（例如计算单应性矩阵至少需要 4 对匹配点）。
模型估计 ：利用这些"内点"估计模型参数（计算 HHH 矩阵）。
验证模型 ：用估计出的模型去测试所有观测数据，计算有多少点符合该模型（即计算 Inliers 的数量）。
迭代更新：重复上述步骤。如果在某次迭代中，内点数量最多，则更新最佳模型。
最终拟合 ：最后使用所有被判定为内点的数据，重新计算最终的矩阵 HHH（通常使用最小二乘法）。

B. 迭代次数

RANSAC 需要运行多少次？这取决于我们希望达到正确结果的概率 ppp、局外点（错误匹配）的比例 eee 以及每次采样所需的点数 sss。公式为：N=log⁡(1−p)log⁡(1−(1−e)s)N = \frac{\log(1-p)}{\log(1-(1-e)^s)}N=log(1−(1−e)s)log(1−p)。

几何变换类型影响 sss：不同的变换需要不同的最少点数（如仿射需要3点，单应性需要4点），因此需要的迭代次数也不同。

要的最少迭代轮数与几何变换类型有关。为什么

我们可以通过三个步骤来拆解这个逻辑：

1. 核心变量：样本数 sss

RANSAC 的每一次迭代，都要先随机抽取一组**"最少样本集"**来计算模型。这个"最少样本数"记为 sss。

不同的几何变换，自由度（DOF）不同，导致解出方程所需的最少点对数量 (sss) 也不同：

平移变换 (Translation): 2 个自由度 →\rightarrow→ 1 对点提供 2 个方程 →\rightarrow→ s=1s=1s=1 (只要 1 个点就能算出平移量)。
相似变换 (Similarity): 4 个自由度 →\rightarrow→ s=2s=2s=2 (需要 2 个点)。
仿射变换 (Affine): 6 个自由度 →\rightarrow→ s=3s=3s=3 (需要 3 个点)。
单应性变换 (Homography): 8 个自由度 →\rightarrow→ s=4s=4s=4 (需要 4 个点)。

2. 概率陷阱：指数级难度

假设在一堆数据中，好点（内点）的比例是 www （比如 50%，即 w=0.5w=0.5w=0.5）。

我们要一次性 连续抽中 sss 个好点，才能算出一把正确的模型。只要其中混入 1 个坏点，这次计算就废了。

一次抽样成功的概率是：

P(Success)=wsP(\text{Success}) = w^sP(Success)=ws

请注意，sss 是在指数位置上的！

如果是平移 (s=1s=1s=1): 成功率 0.51=50%0.5^1 = 50\%0.51=50%。 (很容易，扔两次硬币就能对一次)
如果是仿射 (s=3s=3s=3): 成功率 0.53=12.5%0.5^3 = 12.5\%0.53=12.5%。
如果是单应性 (s=4s=4s=4): 成功率 0.54=6.25%0.5^4 = 6.25\%0.54=6.25%。
(如果是一个更复杂的模型，比如基础矩阵 s=8s=8s=8): 成功率 0.58≈0.39%0.5^8 \approx 0.39\%0.58≈0.39%。 (千分之三的概率)

3. 结论：为什么要更多迭代？

因为随着变换变复杂（sss 变大），单次抽中全好点的概率 (wsw^sws) 会呈指数级下降。

为了保证我们最终能有 99% 的把握 (p=0.99p=0.99p=0.99) 至少找到一次正确的模型，我们需要尝试的次数 kkk 公式如下：

k=log⁡(1−p)log⁡(1−ws)k = \frac{\log(1-p)}{\log(1-w^s)}k=log(1−ws)log(1−p)