hot100-51搜索二维矩阵

一、题目

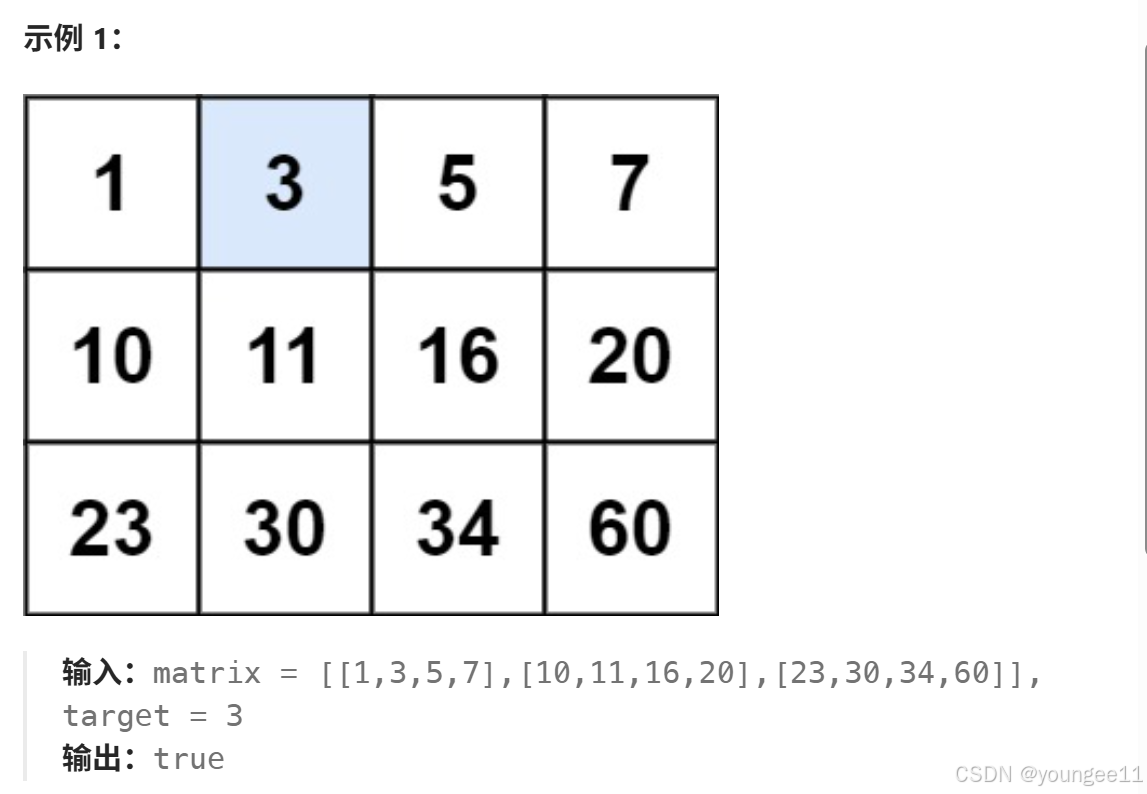
m×n的矩阵，每行中的整数从左到右递增排列，每行第一个整数大于前一行的最后一个整数。

给定矩阵和target，如果target在矩阵中，返回true，否则返回false。

二、思路

1、这个题目和搜索二维矩阵 II 做法可以相同，从右上角开始搜索。如果当前值 大于 target → 向左走（排除这一列）；如果当前值 小于 target → 向下走（排除这一行）；如果相等 → 找到了！

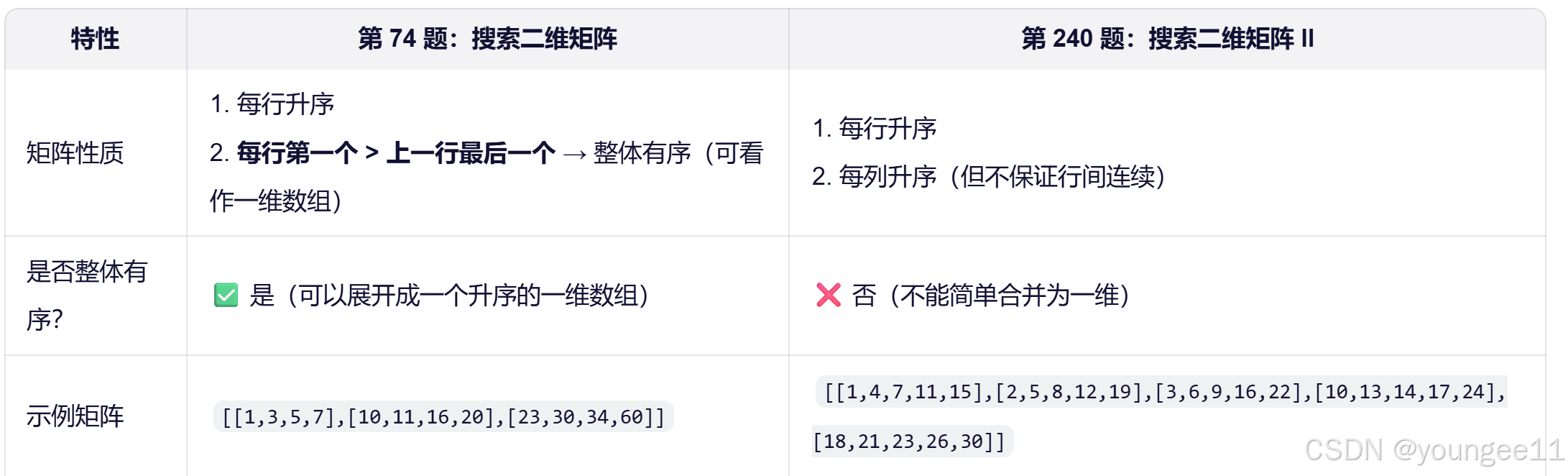
2、这个题目的特性是，每行的第一个元素 > 上一行的最后一个怨怒是，说明所有行是严格递增拼接的，使用上面的解法时间复杂度是O(m+n)，如果使用二分查找时间复杂度是O(log(mn))。

展开为一个一维数组，总长度m x n，在[0,N-1]范围内进行二分查找。对于任意一维索引mid，转换为二维坐标，行号：row=mid/n，列号：col=mid%n。比较matrix[m][n]与target，调整左右边界。

int row = mid / n; // 整除 → 得到"完整行数"

int col = mid % n; // 取余 → 得到"在该行中的偏移"

三、代码

复制代码

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length-1,n = matrix[0].length-1;
        int row = 0, col = n;
        while(row <= m && col >= 0){
            if(matrix[row][col] == target){
                return true;
            }else if(matrix[row][col] > target){
                col--;
            }else{
                row++;
            }
        }
        return false;
    }
}

做法二

复制代码

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length,n = matrix[0].length;
        int left=0,right = m*n -1;
        while(left <= right){
            int mid = left + (right - left) /2;
            int row = mid / n;
            int col = mid % n;
            if(matrix[row][col] == target){
                return true;
            }else if(matrix[row][col] < target){
                left = mid + 1;
            }else{
                right = mid - 1;
            }
        }
        return false;
    }
}