（论文速读）GAT：图注意神经网络

论文题目：Graph Attention Networks （图注意神经网络）

会议：ICLR2018

摘要：我们提出了图注意网络(GATs)，这是一种新颖的神经网络架构，可以在图结构数据上运行，利用隐藏的自注意层来解决基于图卷积或其近似的先前方法的缺点。通过堆叠层，其中的节点能够参与其邻居的特征，我们可以(隐式地)为邻居中的不同节点指定不同的权重，而不需要任何昂贵的矩阵操作(例如反转)或依赖于预先知道的图结构。通过这种方式，我们同时解决了基于频谱的图神经网络的几个关键挑战，并使我们的模型很容易适用于感应和转导问题。我们的GAT模型已经在四个已建立的传导和归纳图基准中达到或匹配了最先进的结果:Cora, Citeseer和Pubmed引文网络数据集，以及蛋白质-蛋白质相互作用数据集(其中测试图在训练期间保持不可见)。

图注意力网络GAT - 让图神经网络学会"关注重点"

引言

在GCN大获成功之后，研究者们开始思考：能否让图神经网络更加智能，学会自动判断哪些邻居更重要？Petar Veličković等人在ICLR 2018发表的Graph Attention Networks（GAT）给出了漂亮的答案。今天我们深入解读这篇将注意力机制引入图学习的经典论文。

动机：GCN的局限

回顾GCN的传播公式：

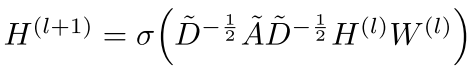
这里的归一化系数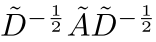是预先计算好的，意味着：

每个邻居的权重是固定的（由图结构决定）
不同邻居的重要性无法自适应学习
依赖于特定的图结构（归纳学习困难）

问题：在社交网络中，并非所有朋友都同等重要；在引用网络中，不同引用文献的相关性也各不相同。我们需要一种机制来学习这种差异化的重要性。

GAT的核心设计

1. 图注意力层（Graph Attentional Layer）

输入：节点特征集合

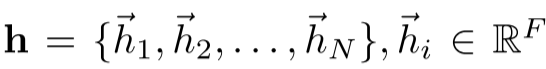
输出：新的节点特征

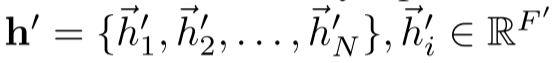
步骤：

Step 1 - 线性变换 ：首先对所有节点应用共享的线性变换（权重矩阵）：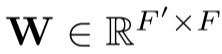

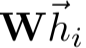
Step 2 - 注意力系数计算：使用注意力机制a(., .)计算边的重要性：

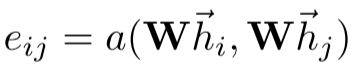
这个系数表示节点j的特征对节点i的重要性。

Step 3 - Masked Attention ：只计算邻居节点的注意力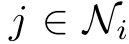，注入图结构信息。

Step 4 - 归一化：使用softmax归一化，使系数跨邻居可比较：

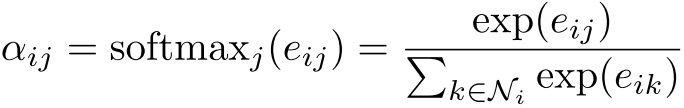
具体实现：论文中使用单层前馈神经网络作为注意力机制：

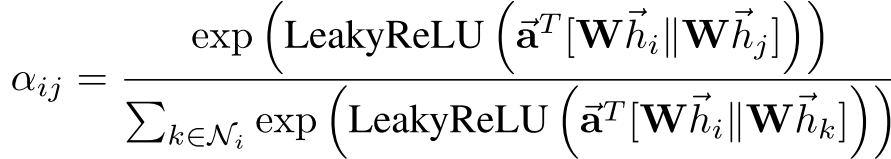
其中：

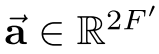是可学习的权重向量
| 表示拼接操作
LeakyReLU的负斜率 = 0.2

Step 5 - 聚合：使用学到的注意力系数聚合邻居特征：

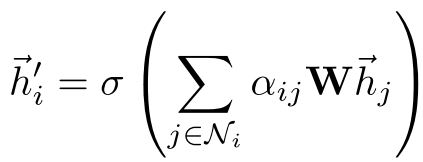
2. Multi-Head Attention（多头注意力）

为了稳定学习过程并增强模型表达能力，GAT采用多头注意力机制（借鉴Transformer）。使用K个独立的注意力头并拼接输出：

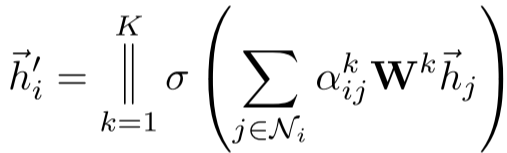
其中|表示拼接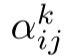，是第k个注意力头计算的系数。

对于最后一层（预测层），使用平均而非拼接：

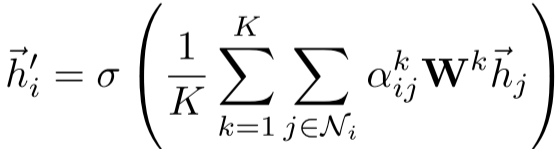
架构设计

转导学习设置（Cora/Citeseer）：

第一层 ：8个注意力头，每头输出8维特征（共64维）
- 激活函数：ELU
第二层 ：单个注意力头，输出C维（类别数）
- 激活函数：Softmax
正则化 ：
- L2正则化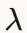： = 0.0005
- Dropout：p = 0.6（应用于输入和归一化的注意力系数）

归纳学习设置（PPI）：

第一层：4个注意力头，每头256维（共1024维），ELU
第二层：4个注意力头，每头256维（共1024维），ELU + Skip Connection
第三层：6个注意力头，每头121维，平均后Sigmoid（多标签分类）
批大小：2个图
无需L2正则化或Dropout

与相关工作的对比

vs. GCN：

计算效率：都是O(|V|FF' + |E|F')，在同一水平
表达能力：GAT可学习不同邻居的权重，GCN权重固定
可解释性：GAT的注意力权重可以可视化分析

vs. GraphSAGE：

邻域采样：GraphSAGE采样固定大小邻域，GAT使用完整邻域
顺序假设：GraphSAGE-LSTM假设邻居有序（通过随机排列缓解），GAT无此假设
归纳能力：都支持归纳学习，但GAT不需要采样

vs. MoNet： GAT可视为MoNet的特殊实例，其中伪坐标函数使用节点特征而非结构属性。

实验结果详解

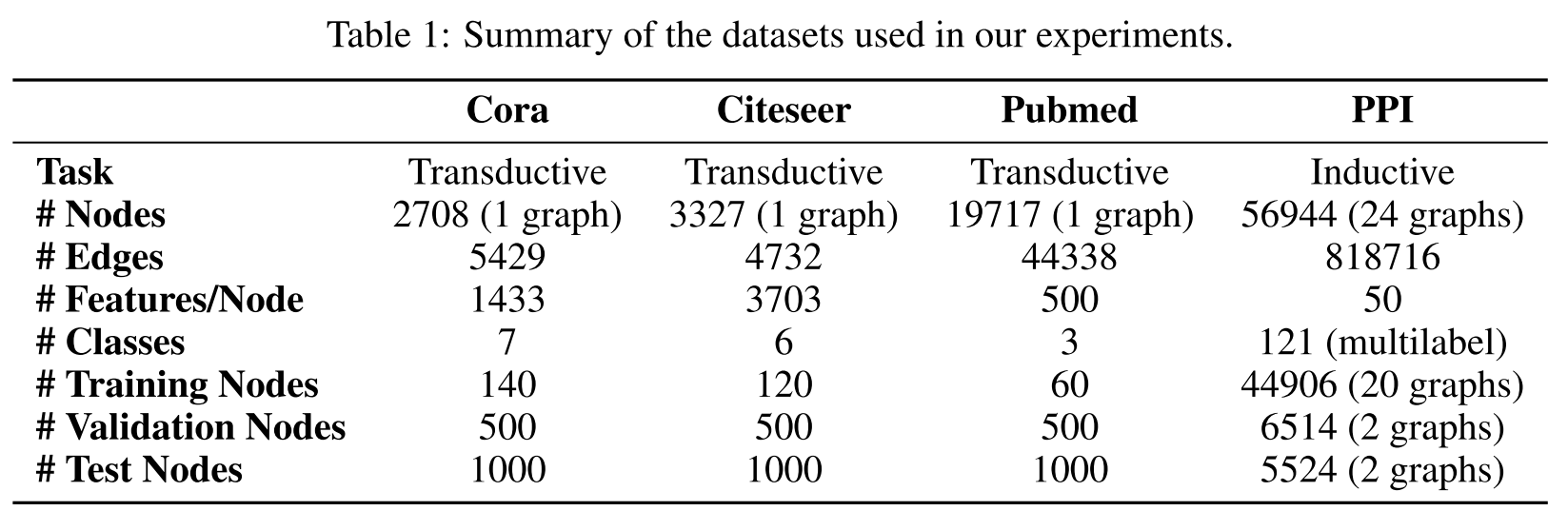
1. 转导学习性能

方法	Cora	Citeseer	Pubmed
MLP	55.1%	46.5%	71.4%
DeepWalk	67.2%	43.2%	65.3%
Planetoid	75.7%	64.7%	77.2%
GCN	81.5%	70.3%	79.0%
GAT	83.0 ± 0.7%	72.5 ± 0.7%	79.0 ± 0.3%

关键发现：

在Cora上比GCN提升1.5%
在Citeseer上比GCN提升2.2%
Pubmed上与GCN持平（可能因为图较为规则）

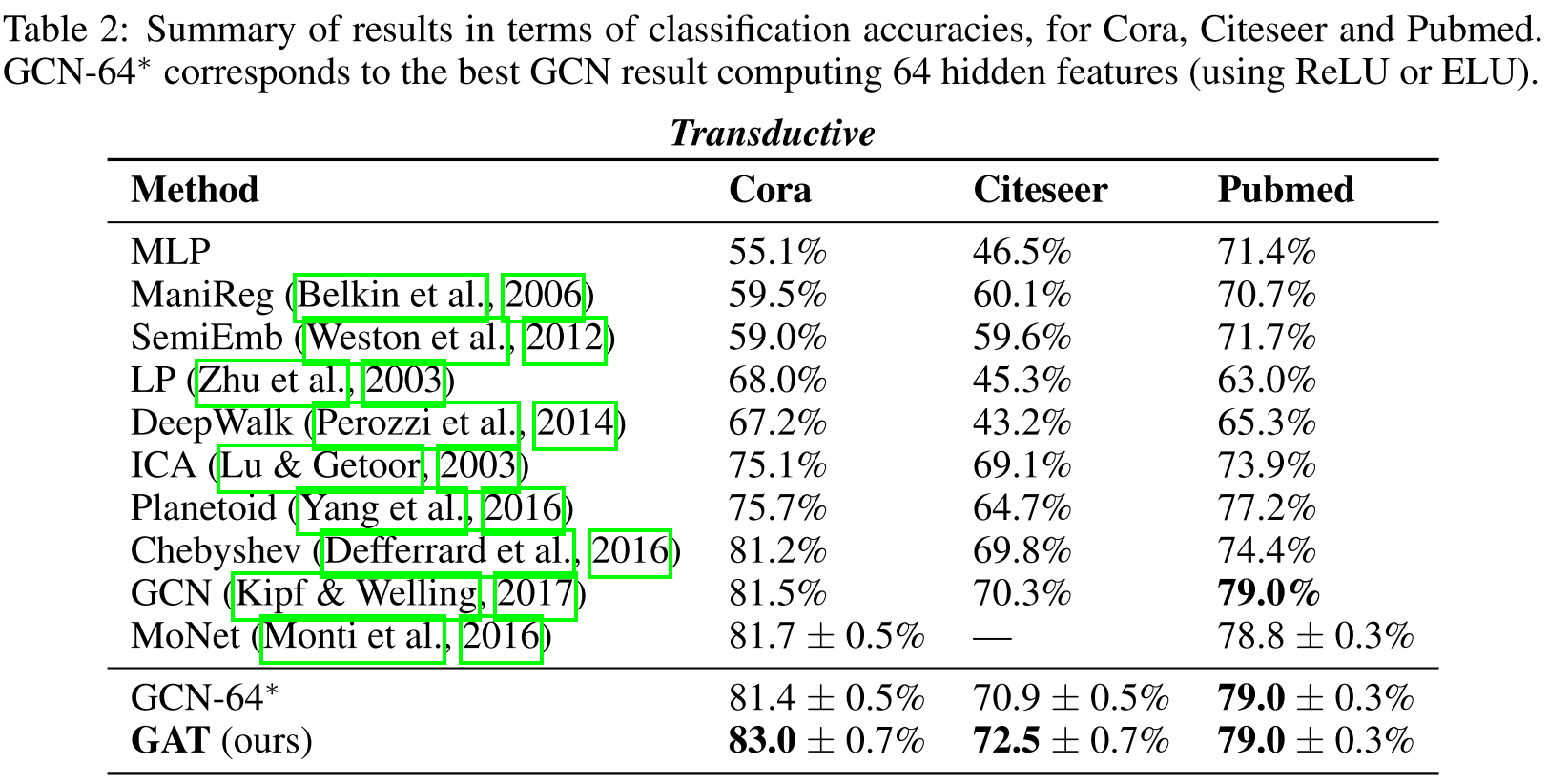
2. 归纳学习性能（PPI数据集）

PPI数据集统计：

训练：20个图，44,906个节点
验证：2个图，6,514个节点
测试：2个图，5,524个节点（训练时完全未见）
特征：50维（位置基因集、motif基因集、免疫学特征）
标签：121个（多标签分类，来自基因本体）

方法	Micro-F1
Random	0.396
MLP	0.422
GraphSAGE-GCN	0.500
GraphSAGE-mean	0.598
GraphSAGE-LSTM	0.612
GraphSAGE-pool	0.600
Const-GAT	0.934 ± 0.006
GAT	0.973 ± 0.002

惊人的发现：

GAT比最佳GraphSAGE方法提升36.1% (0.612 → 0.973)
即使是常数注意力的Const-GAT也达到0.934，说明完整邻域聚合很重要
GAT vs. Const-GAT提升3.9%，证明注意力机制的价值

3. 可视化分析

论文提供了Cora数据集上第一隐藏层的t-SNE可视化：

不同颜色代表7个文档类别
边的粗细表示8个注意力头的平均注意力系数
观察到明显的聚类结构，验证了模型的判别能力

注意力机制的可解释性

注意力权重可以揭示：

哪些邻居对当前节点最重要
不同注意力头关注的模式是否不同
图中的关键结构模式

虽然论文没有深入分析，但指出这是未来的重要研究方向（类似机器翻译中的attention可视化）。

计算复杂度分析

时间复杂度（单个注意力头）： O(|V|FF' + |E|F')

线性变换：O(|V|FF')
注意力计算：O(|E|F')（每条边计算一次）

使用K个注意力头，乘以因子K，但各头计算完全独立可并行。

空间复杂度：

稠密图：O(|V|^2)（存储注意力系数）
稀疏图：O(|E|)（使用稀疏矩阵操作）

论文实现了稀疏版本，将存储复杂度降至线性。

局限与未来工作

论文诚实地讨论了几个限制：

批处理限制：当前稀疏实现只支持rank-2张量的稀疏乘法，限制了批处理能力
GPU效率：对于非常稀疏的图，GPU相比CPU可能没有明显优势
感受野深度：与GCN类似，受限于网络深度（ $K$ 层网络的感受野是 $K$ 阶邻域）
重复计算：在分布式场景下，高度重叠的邻域会导致冗余计算
边特征：当前版本不直接支持边特征（虽然可以扩展）

总结

GAT通过引入注意力机制，成功解决了GCN的几个关键局限：

核心贡献：

自适应学习邻居重要性（不同邻居不同权重）
保持计算效率（与GCN相当）
支持归纳学习（不依赖固定图结构）
提供可解释性（注意力权重可分析）

性能提升：

转导任务：小幅但稳定的提升
归纳任务：巨大提升（36%+）

影响力： GAT已成为图神经网络的标准架构之一，启发了大量后续工作（如GATv2、SuperGAT等）。其核心思想------让模型学会"关注重点"------在图学习中具有普遍价值。

如果你在处理图数据，特别是需要归纳学习或可解释性的场景，GAT绝对值得一试！