线代第二章矩阵第九、十节：初等变换、矩阵的标准形、阶梯形与行最简阶梯形、初等矩阵

初等变换、矩阵的标准形、阶梯形与行最简阶梯形、初等矩阵

这几个概念是线性代数中矩阵化简的核心，是求解线性方程组、计算矩阵秩、求逆矩阵的基础工具，彼此关联紧密。

一、矩阵的初等变换

矩阵的初等变换分为初等行变换 和初等列变换，两者操作规则一致，只是作用对象不同。

1. 定义

设 A 是 m×n 矩阵，以下三种操作称为矩阵的初等行变换：

1. 换行变换 ：交换矩阵的任意两行，记作 （交换第 i,j 行）。
2. 数乘变换 ：用一个非零常数 k 乘以矩阵的某一行，记作 。
3. 倍加变换 ：将某一行的 k 倍加到另一行上，记作 （第 j 行的 k 倍加到第 i 行）。

初等列变换 的定义完全类似，只需将 "行" 换成 "列"，记作 、、

2. 核心性质

1. 可逆性 ：初等变换是可逆的，且逆变换是同类型的初等变换：
   • 换行变换 的逆变换是自身；
   • 数乘变换 的逆变换是 ；
   • 倍加变换 的逆变换是 。
2. 等价矩阵 ：若矩阵 A 经过有限次初等变换得到矩阵 B，则称 A 与 B 等价 ，记作 A≅B。等价矩阵的性质：
   • 反身性：A≅A；
   • 对称性：若 A≅B，则 B≅A；
   • 传递性：若 A≅B 且 B≅C，则 A≅C；
   • 等价矩阵的秩相等：。

二、阶梯形矩阵与行最简阶梯形矩阵

通过初等行变换，任何矩阵都可以化为阶梯形矩阵和行最简阶梯形矩阵，这是矩阵化简的核心目标。

1. 阶梯形矩阵（行阶梯形）

定义（满足两个条件）

1. 矩阵的零行（所有元素都为 0 的行）全部位于非零行的下方；
2. 各非零行的首非零元（从左到右第一个不为 0 的元素，也称主元）的列标，随着行标的增大而严格增大。

示例（3×4 阶梯形矩阵）

2. 行最简阶梯形矩阵

定义（在阶梯形矩阵基础上增加两个条件）

1. 各非零行的首非零元都是 1；
2. 每个首非零元所在列的其他元素都为 0。

示例（3×4 行最简阶梯形矩阵）

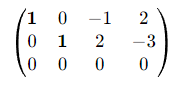
3. 化简步骤（初等行变换法）

4. 核心作用

• 阶梯形矩阵：直接读出矩阵的秩（秩 = 非零行的行数）；
• 行最简阶梯形矩阵：求解线性方程组的通解、求逆矩阵的初等变换法的核心步骤。

三、矩阵的标准形

1. 定义

对于 m×n 矩阵 A，若其秩为 r，则 A 等价于唯一的矩阵

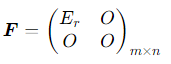
其中 Er​ 是 r 阶单位矩阵，O 是零矩阵。这个矩阵 F 称为 A 的等价标准形（简称标准形）。

2. 化简方法

对矩阵 A 同时进行初等行变换和初等列变换，步骤如下：

1. 先通过初等行变换将 A 化为行最简阶梯形；
2. 再通过初等列变换将主元列以外的列消为零，最终得到标准形。

示例

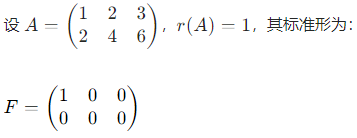
3. 核心性质

1. 任何矩阵的标准形由其行数 m、列数 n、秩 r 唯一确定；
2. 两个矩阵等价 ⟺ 它们的标准形相同；
3. n 阶方阵 A 可逆 ⟺A 的标准形是 n 阶单位矩阵 En。

四、初等矩阵

1. 定义

由单位矩阵 E 经过一次初等变换得到的矩阵，称为初等矩阵。初等矩阵分为三类，对应三种初等变换：

初等变换类型	对应的初等矩阵	记号	示例（3 阶）
交换 E 的第 i,j 行 / 列	换行 / 列初等矩阵	P(i,j)	​​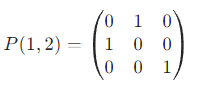
非零常数 k 乘 E 的第 i 行 / 列	数乘初等矩阵	P(i(k))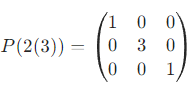
E 的第 j 行的 k 倍加到第 i 行 / 第 i 列的 k 倍加到第 j 列	倍加初等矩阵	P(i,j(k))	​​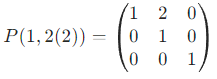

2. 核心定理（初等变换与初等矩阵的关系）

关键结论：对矩阵 A 进行初等行变换 ⟺ 左乘对应的初等矩阵；对 A 进行初等列变换 ⟺ 右乘对应的初等矩阵。

3. 初等矩阵的性质

1. 初等矩阵都是可逆矩阵 ，且其逆矩阵是同类型的初等矩阵：
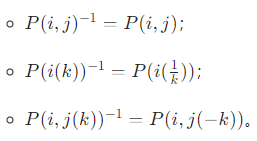
2. 可逆矩阵的等价结论：n 阶方阵 A 可逆 ⟺A 可以表示为有限个初等矩阵的乘积，即A=P1P2⋯Ps其中 P1,P2,...,Ps 均为初等矩阵。
3. 初等矩阵的转置：

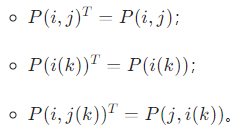
4. 应用：初等变换求逆矩阵的原理

求逆矩阵的初等行变换法 [A∣E]初等行变换​[E∣A−1]，本质是：

Ps​⋯P2​P1​A=E⟹A−1=Ps​⋯P2​P1​

因此 Ps​⋯P2​P1​E=A−1，即对 E 施加相同的初等行变换，就得到 A−1。