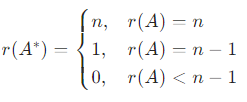线代第二章矩阵第五、六、七节矩阵的转置、方阵的行列式、方阵的伴随矩阵

一、矩阵的转置

1. 定义

对于一个 m×n 矩阵 ，将其行与列互换 后得到的 n×m 矩阵，称为矩阵 A 的转置矩阵，记作 。 的第 i 行第 j 列元素等于 A 的第 j 行第 i 列元素，即：

2. 示例

3. 核心运算性质

设 A,B 为可运算的矩阵，k 为常数，则：

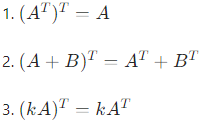
4. 特殊转置矩阵

• 对称矩阵 ：，满足 （如单位矩阵 E、对角矩阵）。
• 反对称矩阵 ：，满足，且主对角线元素 。

二、方阵的行列式

1. 定义

只有方阵 （行数 = 列数）才有行列式。对于 n 阶方阵 ，其行列式记作 ∣A∣ 或 det(A)，是一个标量值（实数或复数），由所有元素的特定组合运算得到。

2. 核心运算性质

设 A,B 为 n 阶方阵，k 为常数，则：

1. 转置行列式不变 ：。
2. 数乘行列式 ：（区别于矩阵数乘 kA 的元素缩放）。
3. 乘积行列式：∣AB∣=∣A∣∣B∣（可推广到多个方阵乘积）。
4. 可逆性判定 ：方阵 A 可逆 ⟺ （此时 A 称为非奇异矩阵 ；∣A∣=0 为奇异矩阵）。
5. 逆矩阵行列式 ：若 A 可逆，则 。
6. 行 / 列变换性质 ：
   • 交换两行 / 列，行列式变号；
   • 某行 / 列乘以常数 k，行列式变为原来的 k 倍；
   • 某行 / 列的倍数加到另一行 / 列，行列式不变

三、方阵的伴随矩阵

1. 定义

对于 n 阶方阵 A=(aij​)，将其每个元素 aij​ 替换为对应的代数余子式 Aij​ ，再将得到的矩阵转置，所得到的 n 阶方阵称为 A 的伴随矩阵，记作 A∗（或 adj(A)）。

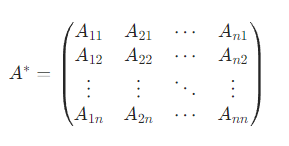
关键注意：A∗ 的第 i 行第 j 列元素是 A 的第 j 行第 i 列元素的代数余子式 Aji​。

2. 示例（2 阶方阵）

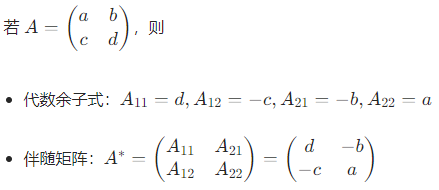
3. 核心定理与性质

核心恒等式：对任意 n 阶方阵 A，有

逆矩阵公式：若 A 可逆（∣A∣=0），则

伴随矩阵的行列式：

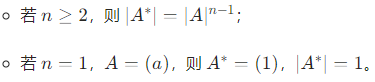
伴随矩阵的转置与逆：

数乘矩阵的伴随：(kA)∗=kn−1A∗（n 阶方阵，k 为常数）。

伴随矩阵的秩：

内容来源-B站宋浩老师