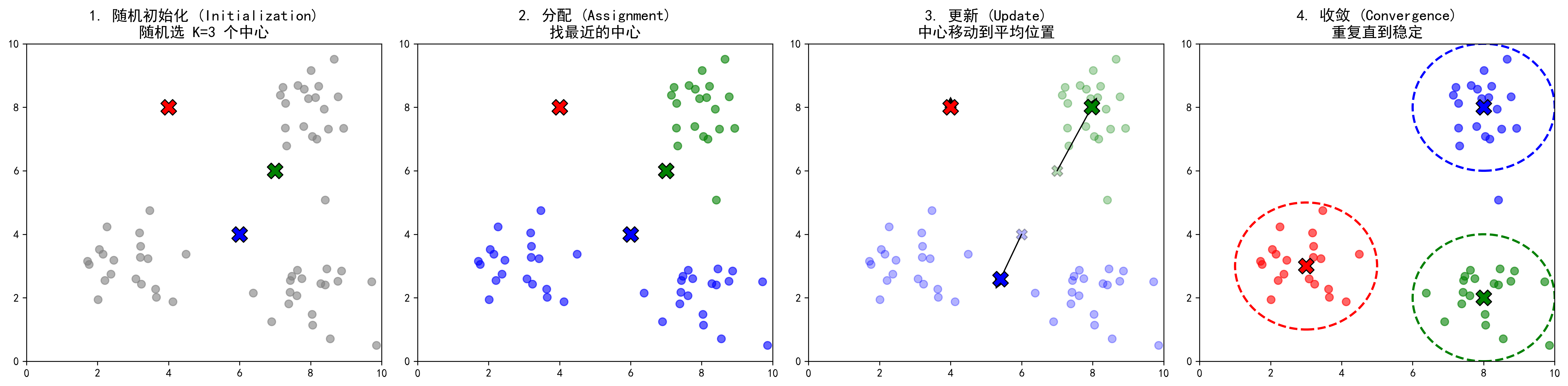
图解说明:
- ❌ 大叉叉:代表"桌长"(聚类中心)。
- 🔴🔵🟢 颜色点:代表不同的"桌子"(簇)。
- ➡️ 箭头:代表桌长为了寻找真正的中心,正在移动。
机器学习里最经典的聚类算法 ------K-Means。
之前我们介绍的算法(比如 SVM、KNN)都是有监督学习 ,也就是老师给了你标准答案(告诉你是猫还是狗)。
但 K-Means 不一样,它是无监督学习 。也就是说,没有标准答案,全靠自己找规律。
如果你完全不懂算法,没关系。想象一下,你是一个婚礼策划师。
1. 它是做什么的?(举个栗子)
你的任务是给 100 位宾客 安排座位。
但是,你完全不认识这些人!你不知道谁是新郎的亲戚,谁是新娘的同事。
你只知道他们的年龄 和职业(这就是数据特征)。
你的目标是:把这 100 个人分成 3 桌(K=3),让每一桌的人尽可能相似,这样他们才有共同话题,不会尴尬。
K-Means 就是帮你干这个的:把一堆杂乱无章的数据,自动分成 K 个堆。
2. K-Means 的"分桌"步骤
K-Means 的工作方式非常像一个不断调整的民主选举。
第一步:随机选"桌长" (初始化)
首先,你心里没底,于是随便指了 3 个人(比如张三、李四、王五)说:"你们三个先当桌长,分别坐到 A、B、C 三张桌子上。"
- 这时候,桌长的位置是随机的,可能很不合理。
第二步:各自找队伍 (分配)
剩下的 97 个人,看这 3 位桌长,谁离自己最近(特征最相似),就坐到谁那一桌去。
- 年轻人可能觉得张三也是年轻人,就去了 A 桌。
- 程序员可能觉得李四也是程序员,就去了 B 桌。
第三步:重新选"桌长" (更新中心)
大家都坐好后,你发现 A 桌虽然大部分是年轻人,但张三其实是个喜欢安静的文艺青年,坐在这一桌吵闹的年轻人中间有点格格不入(他不是真正的中心)。
于是,大家在 A 桌里重新选出一个最能代表这一桌平均水平 的人(真正的中心点),让他当新的桌长。
B 桌、C 桌也同样选出新的中心人物。
第四步:重复折腾 (迭代)
因为桌长换人了(中心点变了),大家发现:"咦?我现在离新的 B 桌桌长更近一点,我不该在 A 桌。"
于是,大家重新站起来,寻找离自己最近的新桌长 。
分好组后,再次选出新的中心...
第五步:尘埃落定 (收敛)
就这样重复了几轮,直到某一次,新的桌长位置不再变化了 (或者变化非常小)。
这时候,分桌结束!
3. 那个 "K" 是什么意思?
K 就是你想要分成的组数。
- 如果你想分 3 桌,K=3。
- 如果你想分 5 桌,K=5。
关键问题:我怎么知道 K 选几?
这确实是个难题。通常我们会试一试:
- K=2,分得太粗糙。
- K=10,分得太细碎。
- 我们会画一条曲线(叫手肘法),找那个"性价比"最高的点。
4. K-Means 的优缺点
✅ 优点 (为什么它好用?)
- 简单快:原理简单,算起来也快,是聚类算法里的"快刀手"。
- 直观:分出来的结果通常很好解释(比如分成了"高消费组"、"低消费组")。
❌ 缺点 (也要注意)
- K 值难定:你必须预先告诉它分几组,如果设错了(比如本来有 3 类,你非要分 2 类),效果会很差。
- 怕"脏"数据:如果有一个人特别离谱(异常值),比如一个 100 岁的老人混进了幼儿园聚会,他可能会把整个组的平均年龄拉大,导致中心点偏离。
- 只喜欢圆圆的团:它假设每一类都是圆圆的一坨。如果数据是弯弯曲曲的形状(比如笑脸形),它就分不好了。
5. 总结
K-Means 就是一个不断纠结的整理控:
- 随机开始:先随便定几个中心。
- 物以类聚:大家找最近的中心抱团。
- 自我修正:根据抱团结果,重新计算中心。
- 循环往复:直到找到最完美的平衡点。
下次你整理衣柜,把衣服分成"夏天穿的"、"冬天穿的"、"运动穿的",其实你就在人肉执行 K-Means 算法!🧹