利用Python挖掘城市数据

K-means

K-means是无监督聚类算法，核心是物以类聚，即根据数据点之间的相似性，把特征相近的点归为一类。

以识别城市热点商圈为例，相似性体现在：

1.空间位置相近（经纬度接近）

2.热度特征相似（人流量、消费金额、商铺密度都高/低）

需注意的点：

K-means算法基于欧氏距离计算数据点的相似度，而不同特征的尺度差异会严重影响结果，如经纬度的数值范围值100+，人流量的数值范围是1000+，如果不标准化，算法会优先被人流量特征这类数值特征主导，因此，用StandardScaler将所有特征转换为均值为0，方差为1的标准分布。最后结果还原时，需要用scaler.inverse_transform将聚类中心还原为真实数据值。

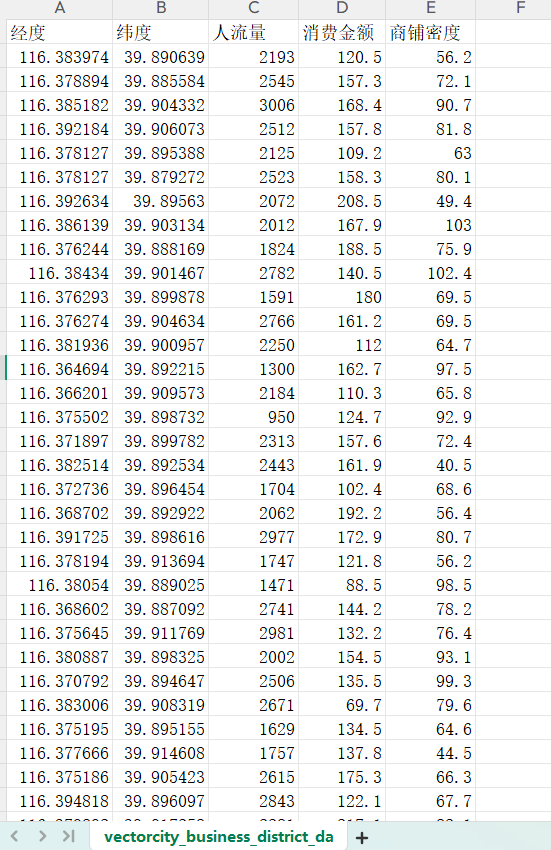
实验数据

完整代码

python 复制代码

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
data=r"C:\Users\Lenovo\Desktop\Python\data\vectorcity_business_district_data.csv"
business=pd.read_csv(data,encoding='utf-8')

#选择聚类特征
features=business[["经度", "纬度", "人流量", "消费金额", "商铺密度"]].copy()
#标准化
scaler=StandardScaler()
features_scaled=scaler.fit_transform(features)
#将标准化特征放回原数据，方便后续查看
feature_names=["经度_标准化", "纬度_标准化", "人流量_标准化", "消费金额_标准化", "商铺密度_标准化"]
business[feature_names]=features_scaled

#设置聚类数量
n_clusters=6
#初始化模型
kmeans=KMeans(n_clusters=n_clusters,random_state=123)
#执行聚类
business['聚类标签']=kmeans.fit_predict(features_scaled)

#还原聚类中心为真实值
cluster_centers=scaler.inverse_transform(kmeans.cluster_centers_)
centers_df=pd.DataFrame(cluster_centers,columns=["商圈核心经度", "商圈核心纬度", "核心区平均人流量", "核心区平均消费", "核心区平均商铺密度"])
print(f'各热点商圈核心特征：{centers_df.round(3)}')

#可视化
plt.rcParams["font.sans-serif"] = ["SimHei"]  
plt.rcParams["axes.unicode_minus"] = False   

fig, ax = plt.subplots(figsize=(12, 9))
scatter=ax.scatter(
    business['经度'],business['纬度'],
    c=business["聚类标签"],#按聚类标签分色
    cmap='viridis',
    s=20,
    alpha=0.8,
    label='商圈数据点'
)
#绘制聚类中心（热点商圈核心位置）
ax.scatter(
    centers_df['商圈核心经度'],centers_df["商圈核心纬度"],
    marker='*',
    color='red',
    s=50,
    label='商圈核心'
)
ax.set_xlabel('经度',fontsize=14)
ax.set_ylabel('纬度',fontsize=14)
ax.set_title("基于k-means的城市热点商圈聚类结果", fontsize=16)
plt.legend()
plt.colorbar(scatter, label="聚类标签（商圈编号）")
plt.tight_layout()
plt.show()

结果输出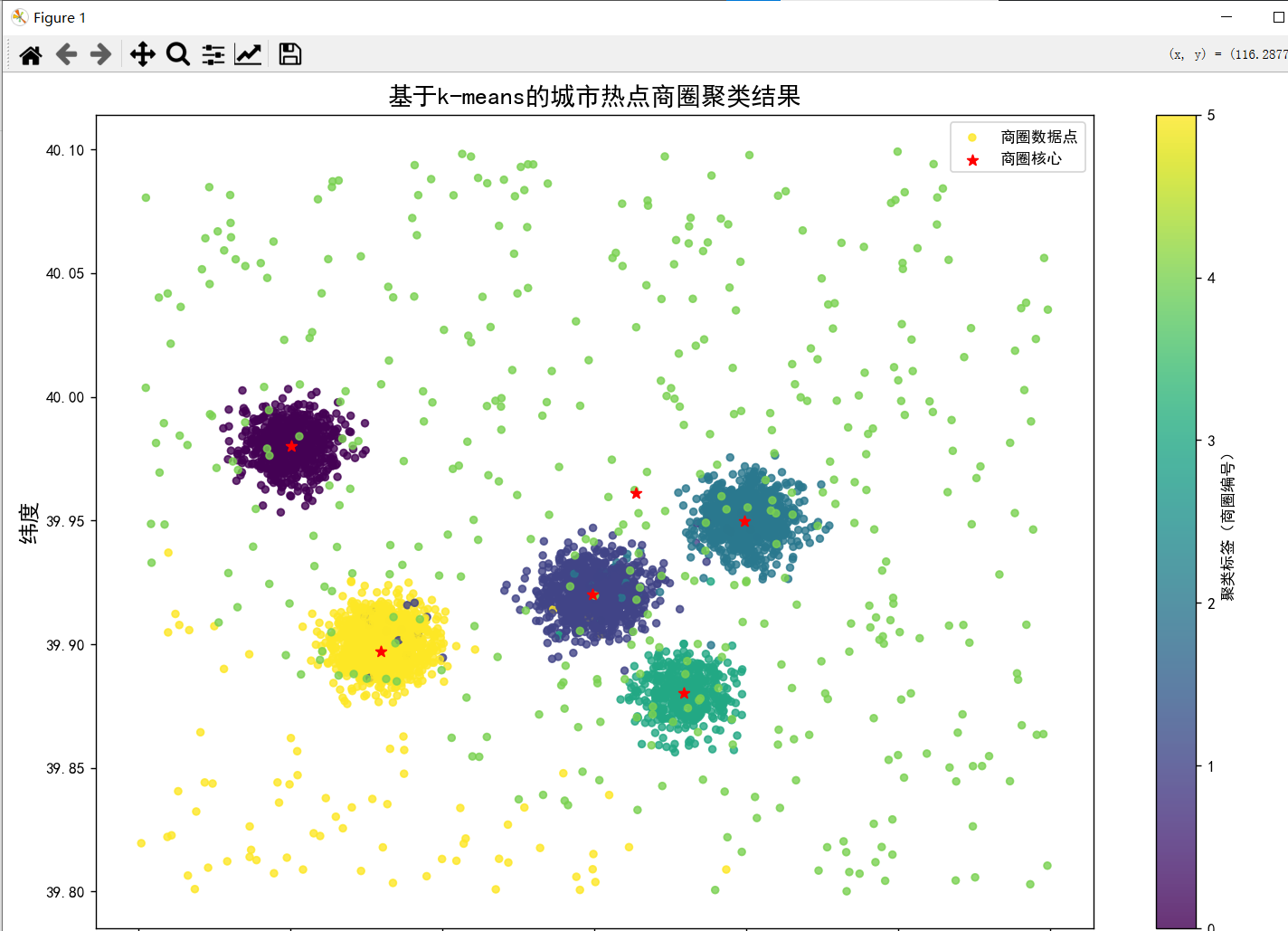

层次聚类

层次聚类是一种无监督聚类算法，核心思想是先把每个数据点当做一个独立的簇，然后按照相似度不断合并或拆分簇，直到满足停止条件，最终形成一个聚类树。分为凝聚式层次聚类和拆分式层次聚类，其中最常用的是凝聚式。

凝聚式流程步骤：

1.初始化：每个数据点 = 1 个独立簇（比如有5000 个数据点，初始有 5000 个簇）；

2.计算：所有簇之间的距离（相似度）；

3.合并：把距离最近的两个簇合并成一个新簇；

4.重复：重复步骤 2-3，直到所有簇合并成 1 个簇（或达到你想要的簇数）

层次聚类的关键是怎么计算两个簇之间的距离，常用4种方式

|-------------|---------------|--------------------|
| 单链接single | 两个簇中最近的两个点的距离 | 适用于检测非球形簇，如长条 |
| 全链接complete | 两个簇中最远的两个点的距离 | 让簇更紧凑，避免链式簇 |
| 平均链接Average | 两个簇中所有点对的平均距离 | 平衡single和complete |
| 沃德链接ward | 合并后簇内平均误差增加最小 | 类似k-means，生成紧凑、球形簇 |

仍然以商圈实验数据，选择沃德链接。

完整代码

python 复制代码

import pandas as pd
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram,linkage,fcluster
from sklearn.preprocessing import StandardScaler
data=r"C:\Users\Lenovo\Desktop\Python\data\vectorcity_business_district_data.csv"
business=pd.read_csv(data,encoding='gbk')

#选择聚类特征
features=business[["经度", "纬度", "人流量", "消费金额", "商铺密度"]].copy()
#标准化
scaler=StandardScaler()
features_scaled=scaler.fit_transform(features)
#将标准化特征放回原数据，方便后续查看
feature_names=["经度_标准化", "纬度_标准化", "人流量_标准化", "消费金额_标准化", "商铺密度_标准化"]
business[feature_names]=features_scaled

#构建层次聚类的linkage矩阵
linkage_matrix=linkage(features_scaled,method='ward',metric='euclidean')

#可视化
plt.rcParams["font.sans-serif"] = ["SimHei"]  
plt.rcParams["axes.unicode_minus"] = False   
#绘制树状图，展示聚类过程
dendrogram(
    linkage_matrix,
    p=20,#只显示最后20次合并，避免树状图过密
    truncate_mode='lastp',#截断显示
    labels=None,
    show_contracted=True,
    leaf_rotation=90,
    leaf_font_size=8
)
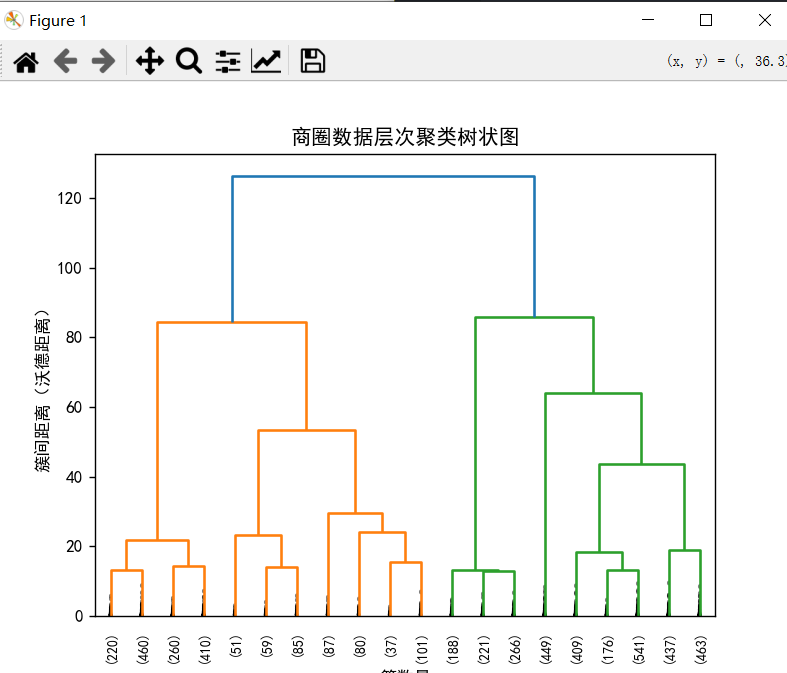
plt.title("商圈数据层次聚类树状图")
plt.xlabel("簇数量")
plt.ylabel("簇间距离（沃德距离）")
plt.show()
#确定簇数并提取聚类结果（两种方式）
#1.看树状图，选择距离突变的阈值
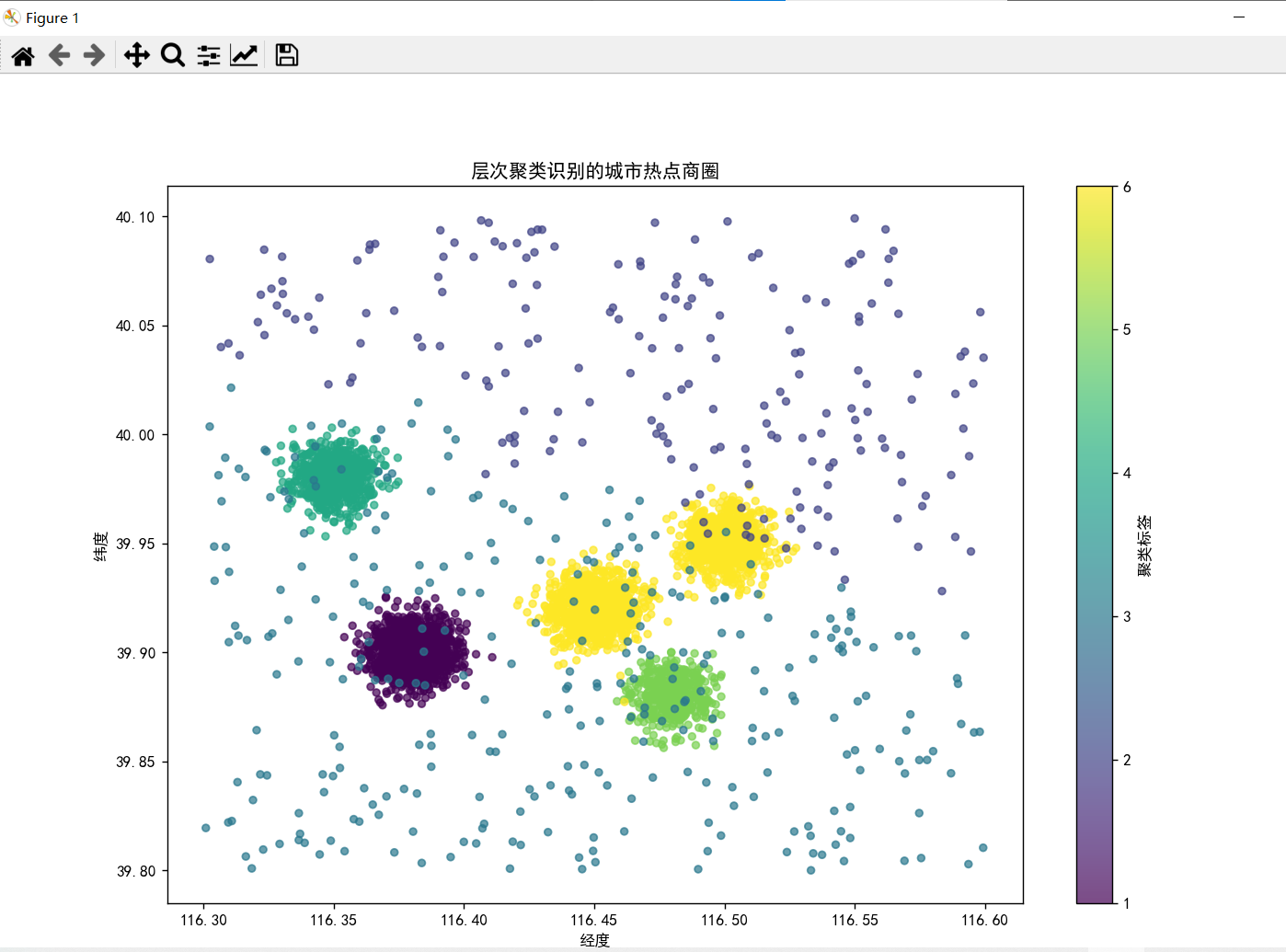
cluster_labels=fcluster(linkage_matrix,t=50,criterion='distance')#距离阈值50

#2.直接指定簇数
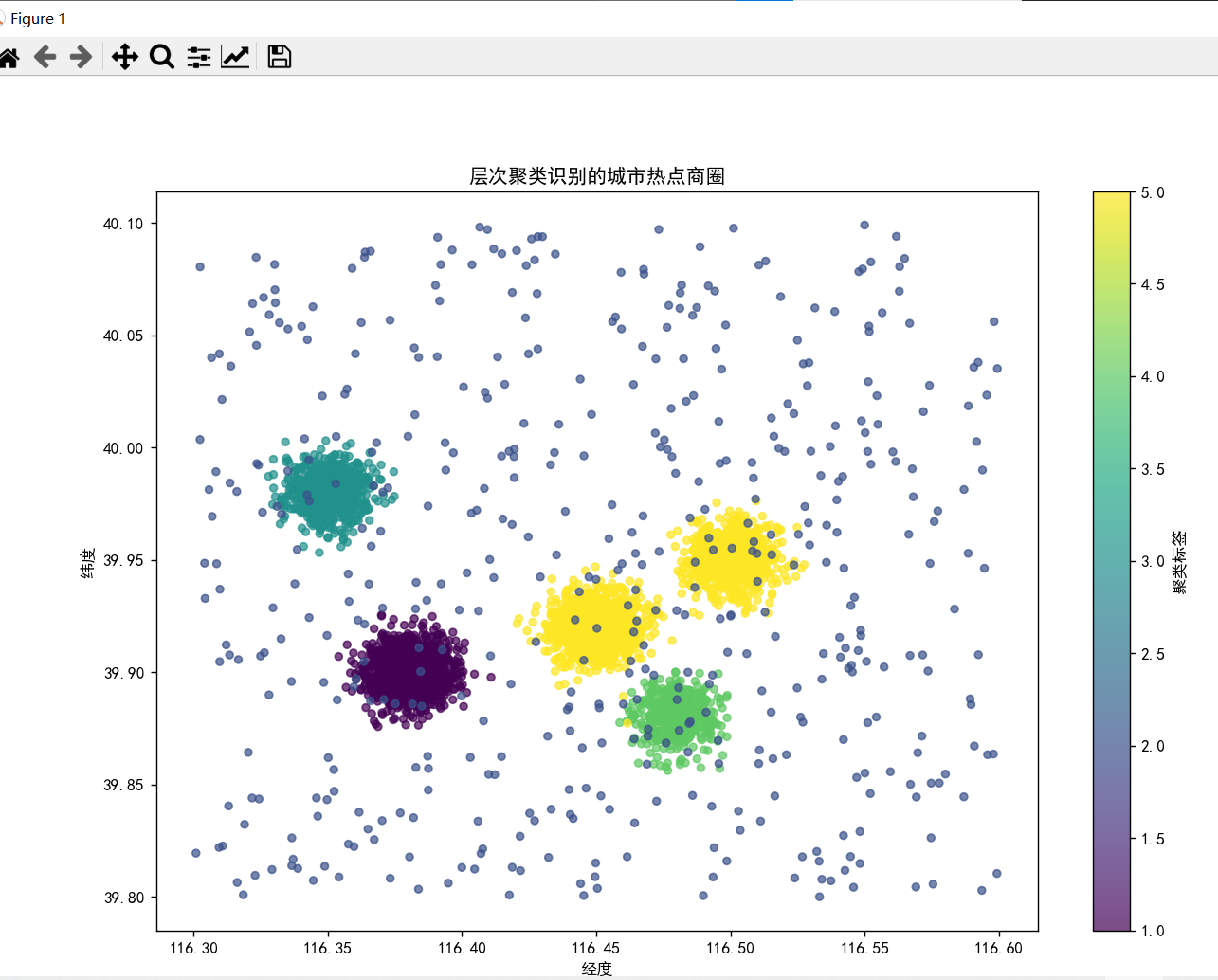
cluster_labels=fcluster(linkage_matrix,t=5,criterion='maxclust')
#把聚类标签添加到原始数据（fcluster标签从1开始）
business["层次聚类标签"]=cluster_labels
plt.figure(figsize=(12,9))
scatter=plt.scatter(
    business['经度'],business['纬度'],
    c=business['层次聚类标签'],
    cmap='viridis',
    s=20,
    alpha=0.7
)
plt.xlabel('经度')
plt.ylabel('纬度')
plt.title('层次聚类识别的城市热点商圈')
plt.colorbar(scatter,label='聚类标签')
plt.show()

结果输出

按距离阈值划分簇（距离50）

按手动指定簇数（n=5）

DBSCAN算法

DBSCAN是基于密度的无监督聚类算法，核心思想是根据数据点的空间密度划分簇，把密度相连的点归为一个簇，同时自动识别出噪声点。该算法特点是不依赖预设簇数，能识别任意形状的簇，且对噪声鲁棒性强。

关键概念

邻域ε

以某个数据点p为中心，以ε（epsilon，邻域半径）为半径的圆形区域，称为点p的 ε- 邻域，该区域内的所有点都是p的邻域点。

核心点core point

若某个点p的ε-邻域内，包含的点数量大于等于minpts（最小点数阈值），则p为核心点。

边界点border point

若某个点q的ε-邻域内的点数小于minpts，但q落在某个核心点的ε-邻域内，则q为边界点。

聚类流程与步骤

1.初始化：设定两个核心参数ε（邻域半径）和MinPts（最小点数），标记所有数据点为「未访问」；

2.遍历点：随机选取一个未访问的点p，标记为「已访问」；

3.找邻域点：找到p的 ε- 邻域内的所有点，组成集合N；

4.判断核心点：

若len(N)≥MinPts：p是核心点，新建一个簇，将N中所有点加入簇，再遍历N中的每个点，递归寻找其邻域内的核心点 / 边界点，全部加入当前簇；
若len(N)<MinPts：标记p为「噪声点」（后续若该点被核心点包含，会重新标记为边界点）；

5.重复：继续遍历下一个未访问的点，直到所有点都被访问；

6.结果：所有密度相连的点形成一个簇，未被任何簇包含的点为噪声点。

完整代码

python 复制代码

distances,index=nn_fit.kneighbors(features_scaled)

对每个数据点，计算它到前 MinPts 个最近邻点的欧氏距离，返回两个结果：

distances：二维数组，形状为(数据点数量, MinPts)。比如总共有 5000 个商圈数据点、MinPts=20，那么distances就是(5000, 20)的数组；
- distances[i][0]：第 i 个点到第 1 近邻居的距离；
- distances[i][1]：第 i 个点到第 2 近邻居的距离；
- ...
- distances[i][19]：第 i 个点到第 20 近邻居的距离（因为 MinPts=20，索引是 19）。
index：第二个返回值是每个近邻点的索引（比如第 i 个点的第 1 近邻居是第 j 个点）。

结果输出

python 复制代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn.neighbors import NearestNeighbors
from sklearn.preprocessing import StandardScaler
data=r"C:\Users\Lenovo\Desktop\Python\data\vectorcity_business_district_data.csv"
business=pd.read_csv(data,encoding='gbk')

#选择聚类特征
features=business[["经度", "纬度", "人流量", "消费金额", "商铺密度"]].copy()
#标准化
scaler=StandardScaler()
features_scaled=scaler.fit_transform(features)

#绘制k距离图，确定最优邻域半径
MinPts=20
#计算每个点到第MinPts个最近邻点的距离
nn=NearestNeighbors(n_neighbors=MinPts)
nn_fit=nn.fit(features_scaled)
distances,index=nn_fit.kneighbors(features_scaled)
#提取第 MinPts 个最近邻的距离并排序
k_dist=np.sort(distances[:,MinPts-1],axis=0)[::-1]

#可视化
plt.rcParams["font.sans-serif"] = ["SimHei"]  
plt.rcParams["axes.unicode_minus"] = False  

plt.figure(figsize=(10, 6))
plt.plot(k_dist)
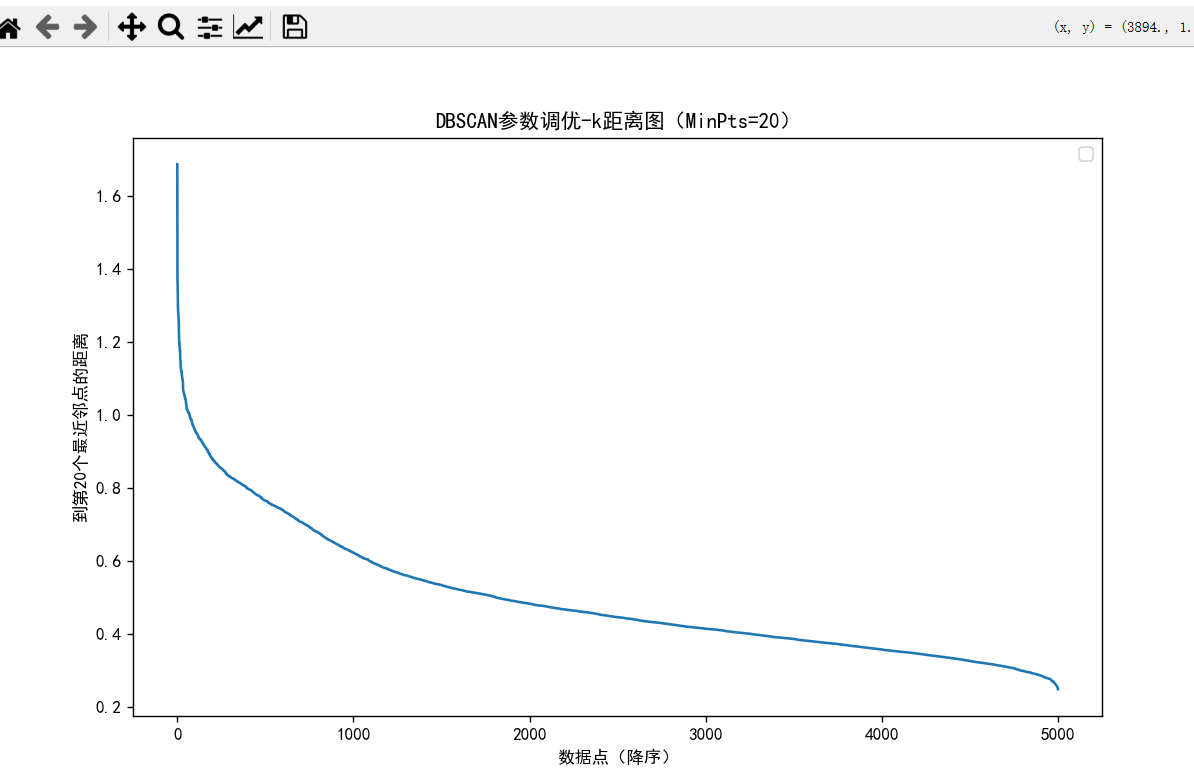
plt.title(f'DBSCAN参数调优-k距离图（MinPts={MinPts}）')
plt.xlabel('数据点（降序）')
plt.ylabel(f'到第{MinPts}个最近邻点的距离')
plt.legend()
plt.show()
#根据距离图的拐点获取最佳eps值
eps=0.75
min_samples=20
#初始化DBSCAN模型
dbscan=DBSCAN(eps=eps,min_samples=min_samples,metric='euclidean')
#执行聚类，获取聚类标签
business['聚类标签']=dbscan.fit_predict(features_scaled)
#注：标签=-1表示噪声点

plt.figure(figsize=(12, 9))
# 绘制噪声点
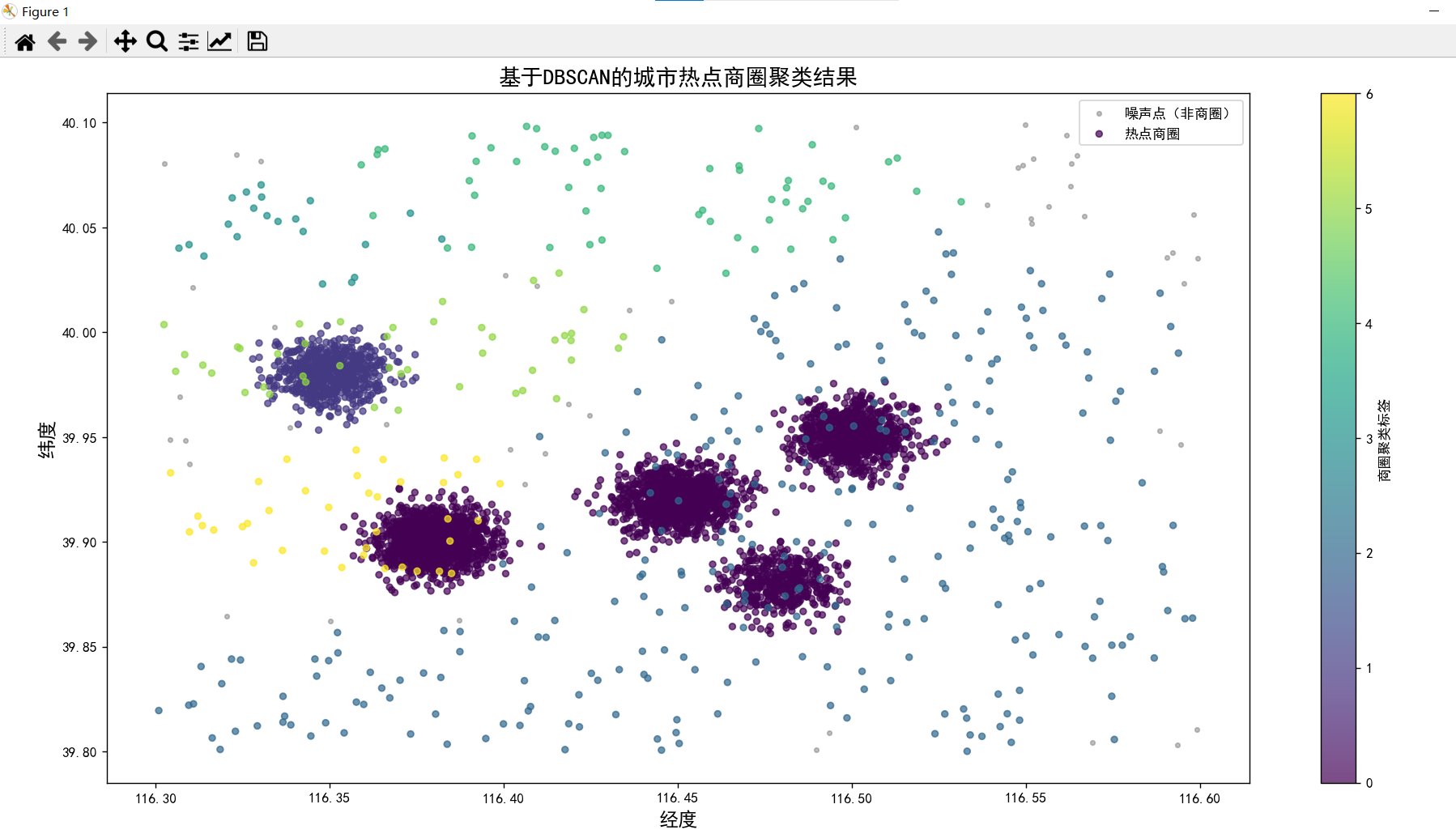
noise = business[business['聚类标签'] == -1]
plt.scatter(noise["经度"], noise["纬度"], c='gray', s=10, alpha=0.5, label='噪声点（非商圈）')
# 绘制商圈簇
cluster = business[business['聚类标签'] != -1]
scatter = plt.scatter(cluster["经度"], cluster["纬度"], c=cluster["聚类标签"], 
                     cmap="viridis", s=20, alpha=0.7, label='热点商圈')
plt.xlabel("经度", fontsize=14)
plt.ylabel("纬度", fontsize=14)
plt.title("基于DBSCAN的城市热点商圈聚类结果", fontsize=16)
plt.colorbar(scatter, label="商圈聚类标签")
plt.legend()
plt.tight_layout()
plt.show()