线代第三章向量第三节：向量间的线性关系二

设 α1,α2,...,αs 是一组 n 维向量，考虑齐次线性组合：

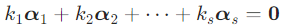
其中 k1,k2,...,ks 是一组实数。

若存在一组 不全为零 的实数 k1,k2,...,ks，使得上述等式成立，则称向量组 α1,α2,...,αs 线性相关 。

若只有当 k1=k2=⋯=ks=0 时 ，上述齐次线性组合等式才成立，则称向量组 α1,α2,...,αs 线性无关。

两向量成比例则组相关若向量组中存在两个向量成比例（如α1=kα2），则这两个向量线性相关，进而整个向量组线性相关。
含零向量的组必相关取零向量对应的系数为 1、其余向量系数为 0（非零组合），可使线性组合为零向量，故含零向量的任意向量组必线性相关。
单独零向量必相关取系数k=1（非零），满足k⋅0=0，故单独一个零向量线性相关。
单独非零向量必无关 若kα=0且α0，则只有k=0，故单独一个非零向量线性无关。
单独向量相关⟺该向量是零向量结合 "3、4"，单独向量的相关性等价于其是否为零向量。
部分组与整体组的关系
- 部分组相关⟹整体组相关（添加向量不改变相关性）；
- 整体组无关⟹部分组无关（删减向量不改变无关性）。
接长 / 截短向量组的关系
- 无关向量组 "接长"（给每个向量增加分量）后仍无关（约束更多，仅零解）；
- 相关向量组 "截短"（给每个向量减少分量）后仍相关（原非零解仍满足截短后的方程组）。
**n 个 n 维向量的相关性（行列式判定）**n 个 n 维向量构成的矩阵行列式为D：
- D0⟺向量组线性无关（矩阵满秩）；
- D=0⟺向量组线性相关（矩阵秩不足）。

定理 1：线性相关的等价条件 向量组α1,...,αs线性相关 ⟺ 该组中至少存在一个向量，可由其余s−1个向量线性表示。
- 证明思路：由线性相关的定义（存在不全为零的系数k1,...,ks，使k1α1+⋯+ksαs=0），取其中一个非零系数对应的向量，即可将其表示为其余向量的线性组合。
定理 2：无关组的表示唯一性 若α1,...,αs线性无关，且α1,...,αs,β线性相关，则β可由α1,...,αs唯一线性表示。

该定理是判断向量组相关性的重要工具：

两个等价的线性无关向量组，所含向量的个数必相同。