在实际研究与工程优化中,我们常常面临这样的问题:影响因素多、组合方案多,但试验成本和时间却十分有限。如何用尽可能少的试验次数,找出关键因素与最优水平组合?正交试验设计正是为解决这一难题而生。
本文将介绍**++正交表生成、正交试验设计、极差分析与方差分析,以及会补充介绍其他试验设计方法++** ++(如析因设计、均匀设计、响应面设计)++。
一、正交表结构与生成
正交表是正交试验设计的核心工具,用于在有限试验次数下,科学安排多因素、多水平的组合方案。其结构本质上是一张标准化的试验安排表,具有严格的数学性质,能够保证各因素水平组合的均衡性与可比性。
1、正交表的结构
(1 )因素与水平
在正交试验设计中,因素与水平是构建试验方案的两个最基本概念,它们共同决定了试验研究的对象和范围。
- **因素:**是指对试验结果可能产生影响的自变量。例如在工艺优化中,温度、时间、原料配比。
- **水平:**是指某一因素在试验中所取的不同状态或取值。例如温度可取20℃、40℃、60℃。在正交表中,通常用数字 1、2、3 等对各水平进行编码,以便于试验安排。
(2 )正交表核心结构
从整体结构看,正交表通常记为𝐿ₙ( 𝑚 ᵏ) 。其中:
- L 代表"正交表";
- n 表示试验次数(即表中的行数);
- m 表示每个因素的水平数;
- k 表示正交表中最多可安排的因素列数。
举例说明: 𝐿₉(3⁴)
- L:代表"正交表"。
- 下标 9:代表这张表一共需要做 9 次实验(表的行数)。
- 括号里的 3:代表表中每个因素(列)都有 3 个水平,用数字1, 2, 3表示。
- 指数 4:代表这张表最多可以安排 4 个因素(表的列数)。
- 所以,L₉(3⁴) 直译就是:一个最多能安排4个三水平因素,且仅需做9次实验的正交表。
2、正交表的生成
在SPSSAU【实验/医学研究】模块,选择【正交试验】,选择因子(因素)个数、对应水平数,然后点击"开始分析"按钮,即可得到对应正交表,操作如下图: 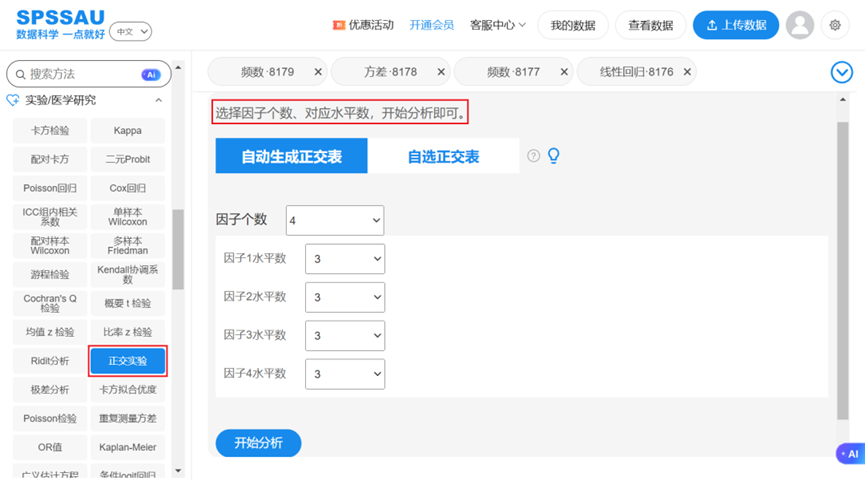
SPSSAU输出四因素三水平正交表如下:
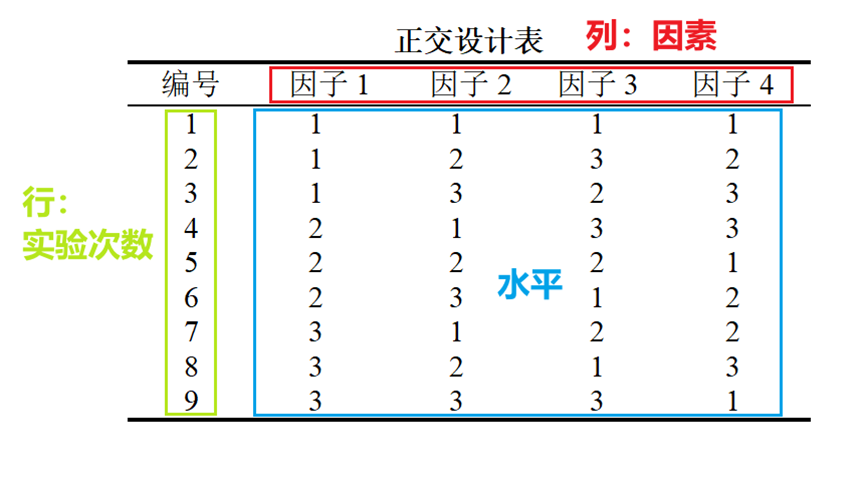
SPSSAU默认找到最接近的标准正交表,比如预期找3个因素的正交表,3个因素分别有3,4或5个水平。若生成的正交表与预期因素数水平数不一致,需要结合拟水平法,组合法,并列法对正交表进行改造,具体可查看下方帮助手册说明:
3、正交表的性质
正交表之所以强大,是因为它具备 "正交性" ,主要体现在两点:
(1 )均匀分散性
均匀分散性是指正交表所选取的试验方案在整体试验空间中分布均匀,任意两列因素的水平组合齐全且出现次数相等。例如,在四因素三水平正交表中,任意两列可以形成 9 种水平组合:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)、(3,3),且每种组合在试验中出现的次数相同,从而保证试验点对整体组合空间具有良好的代表性。
(2 )整齐可比性
整齐可比性是指正交表结构规则、对称有序,每一列中各水平出现的次数完全相同,从而保证不同水平之间具有良好的可比性。例如,在四因素三水平的正交表中,每一列中数字 1、2、3 均出现 3 次,使得各水平在同等条件下参与试验,便于比较其对试验结果的影响。
补充:正交表具有非唯一性
在给定因素数量和水平数的条件下,正交表并非唯一,可以存在多种满足正交性质的排列形式。因此,不同软件生成的正交表在具体排列顺序上可能存在差异,但只要满足正交表的基本性质,其试验设计和分析结论都是等价且可靠的。所以 SPSSAU 等统计软件生成的正交表大家都可以放心使用。
二、正交试验设计与分析步骤
正交试验设计与分析的一般步骤如下:
1确定因素及水平
明确研究目的和评价指标,同时选取主要影响因素并设置相应水平。
2生成正交表
根据因素数和水平数,使用SPSSAU软件生成正交表,完成试验安排。
3进行正交试验
按照正交表进行试验,记录并汇总试验结果。
4进行极差分析或方差分析
使用SPSSAU进行极差或方差分析,分析各因素对试验指标的影响程度及显著性。
5确定最优水平组合
综合分析结果,确定最优方案并进行结果解释。
三、正交试验案例分析
**案例:**某新材料研发团队正在优化合成工艺,希望提高材料的综合性能评分(0-100分)。经预实验确定了三个关键工艺变量,每个变量设置三个水平,需要通过正交试验寻找最优参数组合。
1、确定因素及水平
案例包括A烧结温度(°C)、B保温时间(min)、C添加剂比例(%),因素水平表如下:
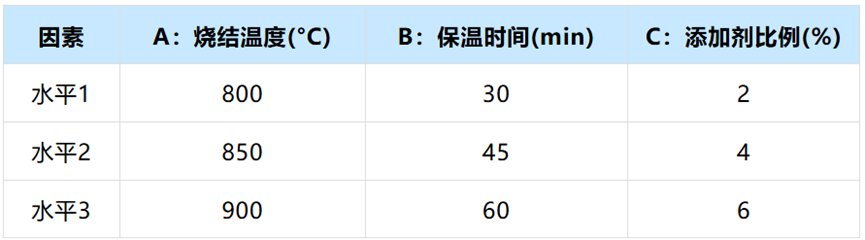
2、生成正交表
根据研究因素水平数可知,应该选择三因素三水平正交表,利用SPSSAU生成三因素三水平正交表如下: 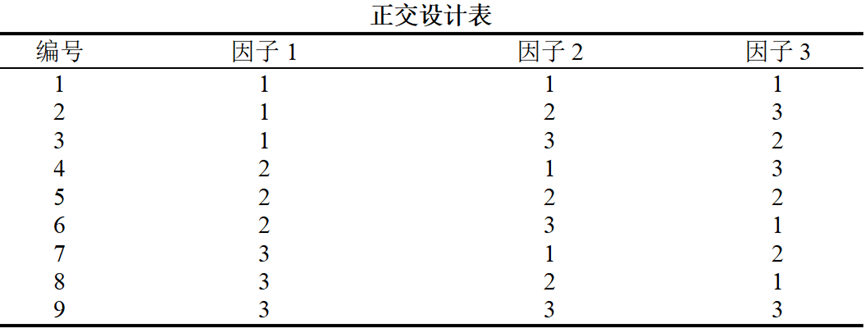
3、进行正交试验
得到正交表后,把表中各列因子下的数字"1"、"2"、"3",分别换成各因素在试验中的水平值,比如A烧结温度(℃)里面的数字1表示800℃、数字2表示850℃,其他因素水平类似。并根据此表格安排试验方案,得到正交试验结果,整理成如下表格:
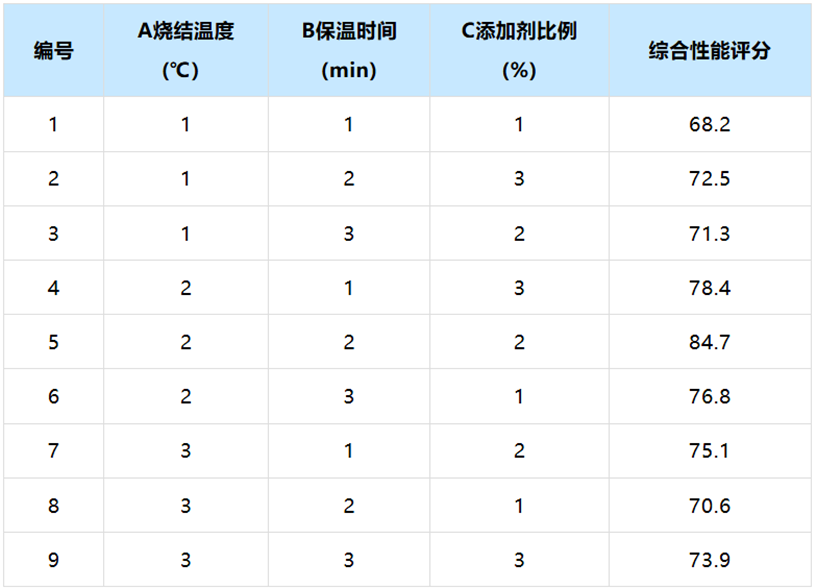
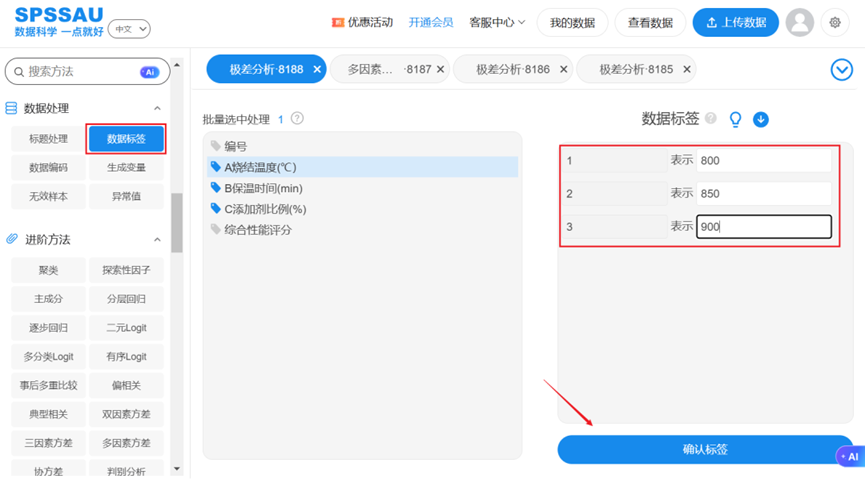
将上表上传数据至SPSSAU系统,可在【数据处理】模块,对因素的各水平设置【数据标签】,如下图:
接下来进行极差分析。
4、进行极差分析
极差分析,也称为直观分析法,是一种非常直观且易于理解的方法。它的核心思想是:通过比较各因素不同水平下实验结果的平均值,来判断该因素对结果影响的大小。
(1 )软件操作
在SPSSAU【实验/医学研究】模块选择【极差分析】,将变量拖拽至右侧对应分析框中,选择试验数据类型为越大越好,代表综合性能评分越大越好,操作如下图:
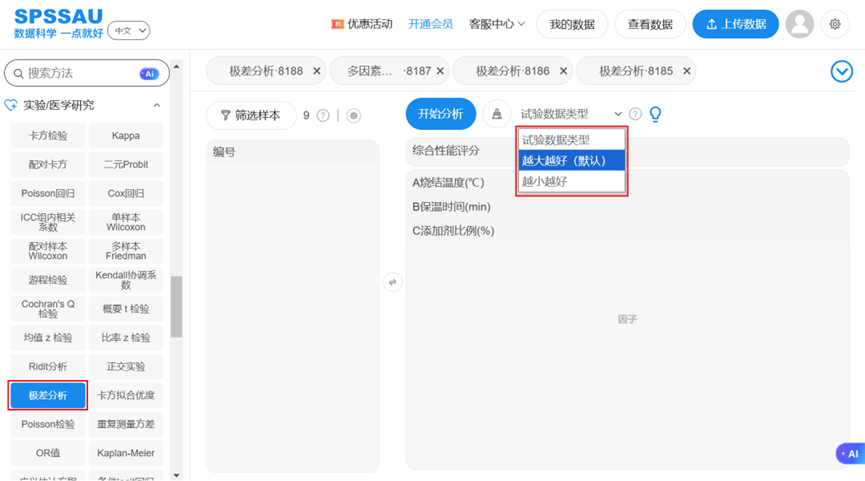
点击"开始分析"按钮,SPSSAU即可输出极差分析结果:
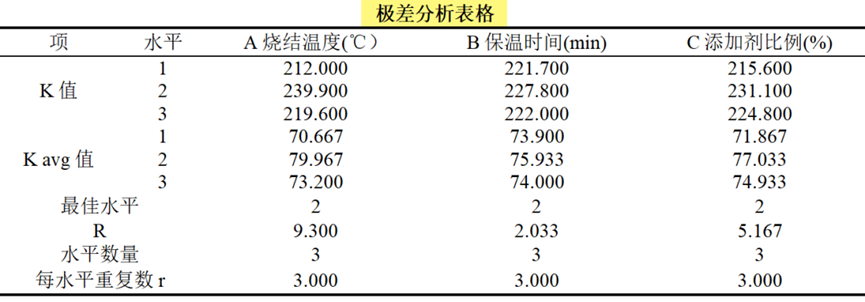
(2 )关键指标解读
极差分析结果中会有多种指标,说明如下:
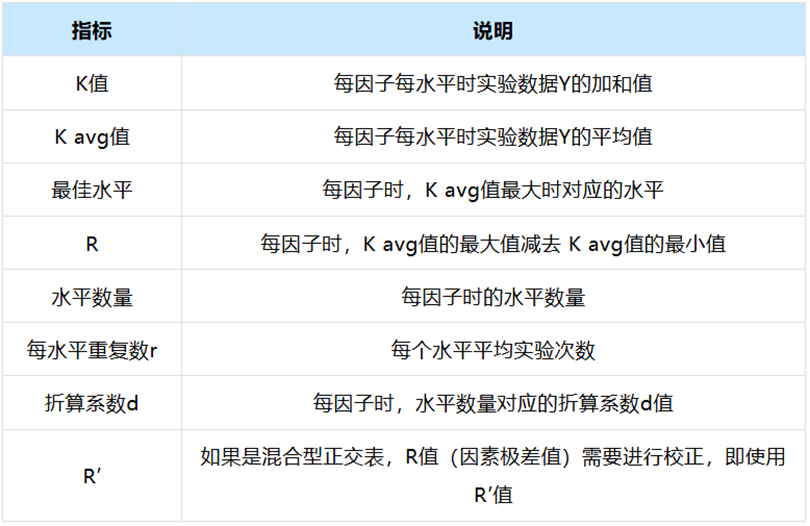
(3 )极差分析结果解读
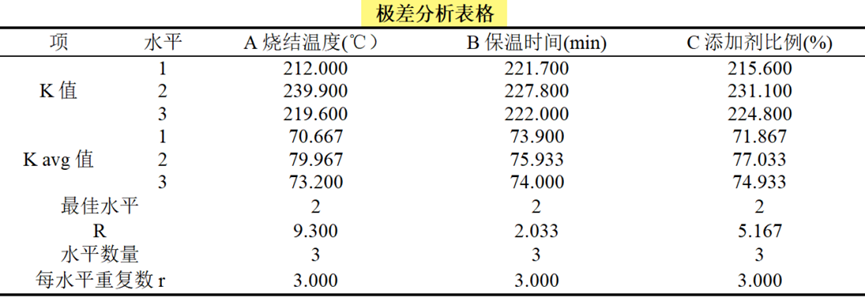
- 首先根据极差R值大小,判断各因素影响程度
A烧结温度(℃)R值最大为主要影响因素;其次是C添加剂比例(%);最后是B保温时间(min)。因此3个因素的重要性排序为:A烧结温度(℃)>C添加剂比例(%)>B保温时间(min)。
- 然后根据K avg值,确定每个因素的最佳水平
从上表可知,因素A、因素B、因素C最佳水平均为水平2。因此综合性能评分最优条件为:A 烧结温度850℃ 、B 保温时间45min 、C 添加剂比例4%。还可通过SPSSAU极差分析输出的"因子各水平均值图"直观判断组合最优水平,如下图:
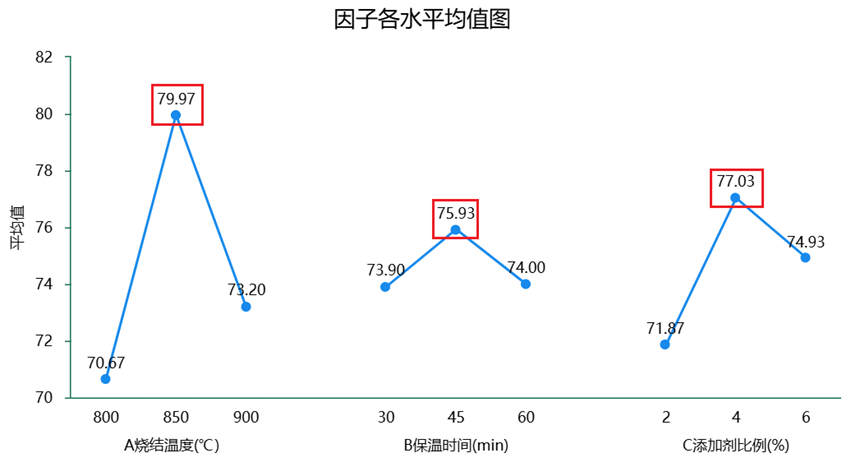
通过上图,可以很直观的看出:A烧结温度(℃)的极差最大(折线高度差最大)为最重要因素,其次是因素C,最后是因素B。三个因素最佳水平均为水平2(折线最高点)。所以综合性能评分最优条件为:A烧结温度850℃、B保温时间45min、C添加剂比例4%。
四、正交试验方差分析
在正交试验中,极差分析用于初步评估各因素影响力度的大小与主次。然而,极差分析无法判断各因素对试验结果的影响是否达到统计显著水平。因此,在实际研究中,可以进一步通过方差分析对正交试验结果进行检验,以验证因素影响的统计显著性。
(1)正交试验极差分析与方差分析对比

(2)方差分析软件操作与分析
在SPSSAU【进阶方法】模块选择【多因素方差】,将变量拖拽至右侧分析框中,若要进行事后多重比较,可自主选择,操作如下图:
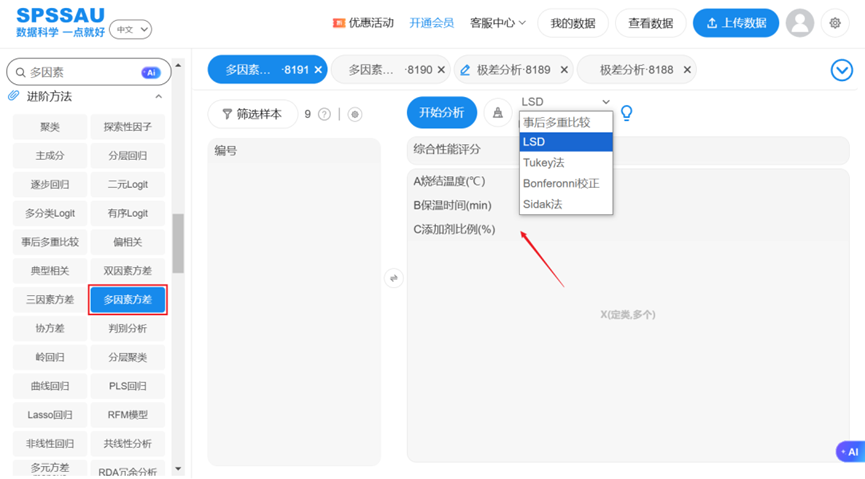
点击"开始分析"按钮,即可得到多因素方差分析结果,如下表:
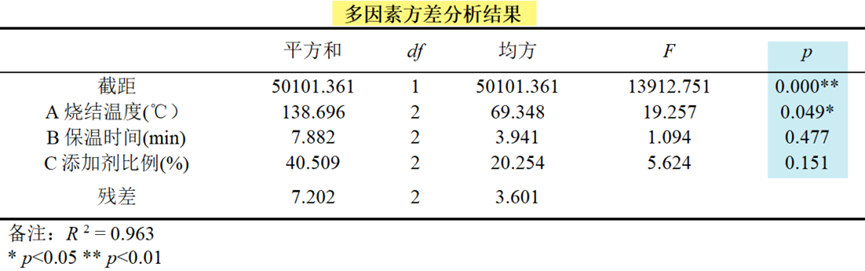
方差分析结果表明:在本实验条件下,仅有因素A烧结温度(℃)对产品综合性能评分有显著影响,因素B与因素C对结果影响均不显著。
五、其他实验设计方法
除了正交试验,还有几种常用的实验设计方法,例如析因设计、均匀设计以及响应面设计。这些实验设计方法各有特点,适用于不同的研究场景。对比说明如下:
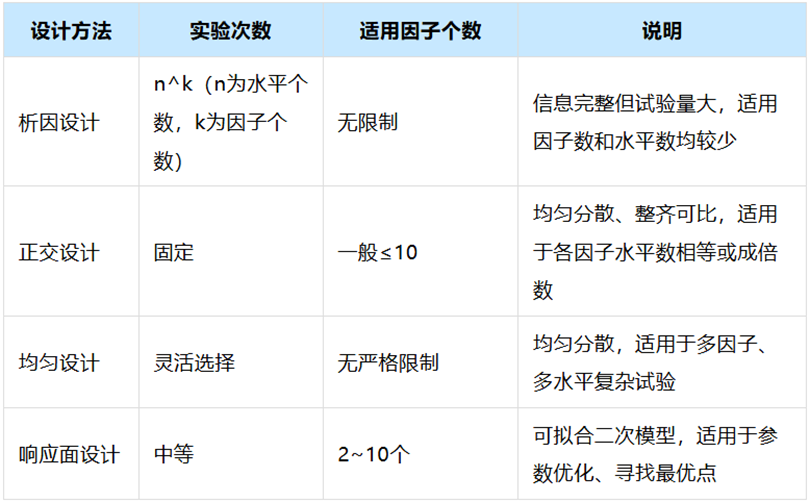
1 析因设计
研究多个因素及其交互作用,通过所有因素水平的组合进行试验,能全面分析因素影响。适用于因素和水平较少时使用,如新产品开发或过程优化。
2 正交设计
是一种基于正交表安排试验的多因素多水平实验设计方法,具有"均匀分散、整齐可比"性。正交设计适用于各因素水平数相等或成倍数且10个以内的因素情况。
3 均匀设计
原则是使试验点在试验空间内分布均匀,相对于正交设计,均匀设计更强调'均匀分散性',但其无'整齐可比性'特点,对因子个数限制少,实验次数也非常灵活。
4 响应面设计
适用于2~10个因子时但响应面设计可偏向于分析角度,比如需要拟合二次模型,寻找最优点等。