【数据结构】常见排序

本篇将介绍一下常见的排序。

1.插入排序和冒泡排序

先看一下插入排序（左图）和冒泡排序（右图）。

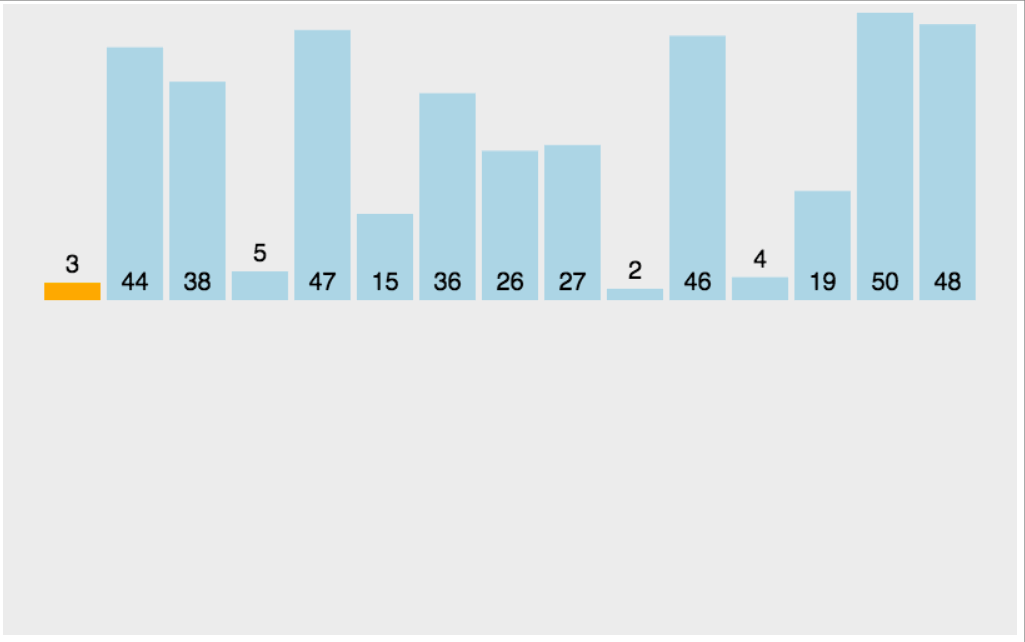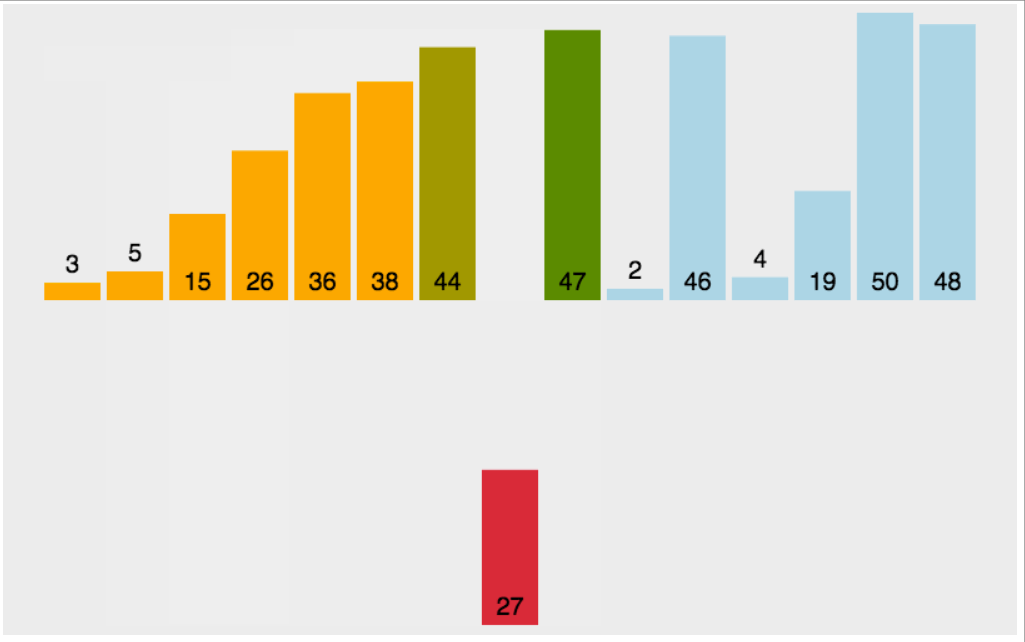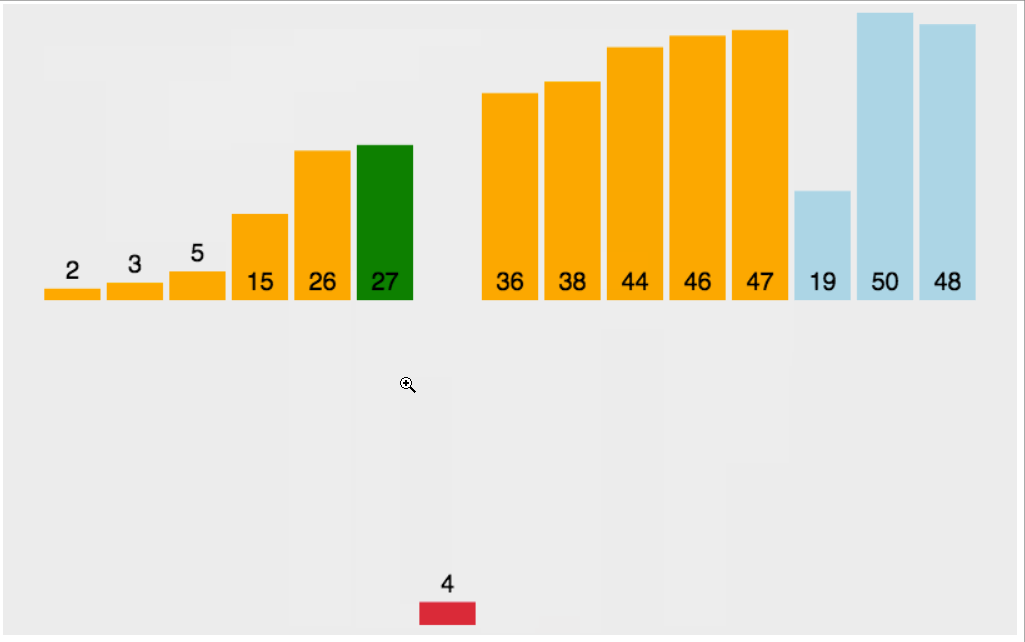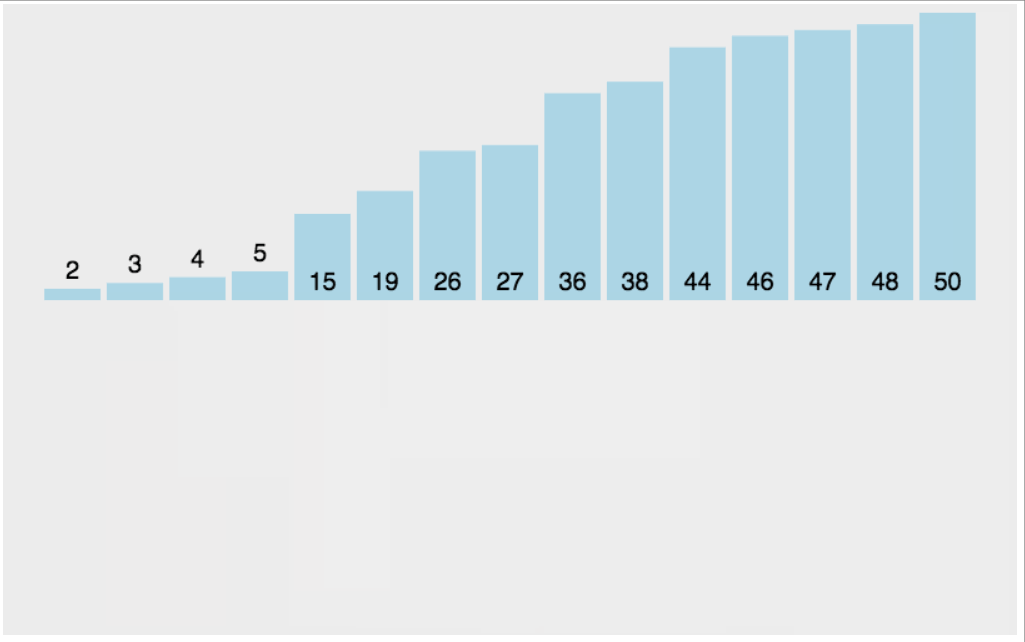
插入排序代码实现

当插入第i(i>=1)个元素时，前面的array[0],array[1],...,array[i-1]已经排好序，此时用array[i]的排序码与array[i-1],array[i-2],...的排序码顺序进行比较，找到插入位置即将array[i]插入，原来位置上的元素顺序后移。
这里需要注意的是，我们对2进行排序的时候，2是最小的，因为是和前一个比较，所以当2已经到了下标为0的位置的时候，就不需要再比较了，所以下面的j只需要>0，不用等于0。
下面是参考代码：

#include <stdio.h>

void Print(int* arr, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}

void Swap(int* p1, int* p2) //交换
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void InsertSort(int* arr, int n) //插入排序
{
	for (int i = 1; i < n; i++)
	{
		for (int j = i; j > 0; j--)
		{
			if (arr[j - 1] > arr[j]) //当前数比前一个小，就交换位置
			{
				Swap(&arr[j - 1], &arr[j]);
			}
			else //当前数小于或等于前一个数，直接退出
			{
				break;
			}
		}
	}
}

int main()
{
	int arr[] = { 30,5,12,34,7,26,87,4,39 };
	int n = sizeof(arr) / sizeof(arr[0]);
	Print(arr, n);
	InsertSort(arr, n);
	Print(arr, n);
	return 0;
}

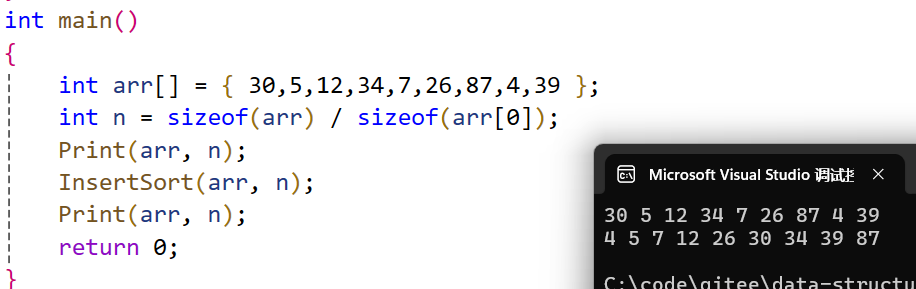
插入排序是将排好的数往后移，不是一个一个交换，是保存当前数，往后移动比它大的数，一个个交换效率特别低！

插入排序的时间复杂度是。当数组为逆序的时候，时间复杂度最高，数组为顺序的时候，时间复杂度可为。

冒泡排序参考代码

冒泡排序就是把大的往后挪。

void BubbleSort(int* arr, int n) // 冒泡排序
{
	for (int j = 0; j < n; j++)
	{
		for (int i = 1; i < n - j; i++)
		{
			int t = arr[i];
			if (arr[i - 1] > arr[i]) //前一个比后一个大就交换
			{
				Swap(&arr[i - 1], (&arr[i]));
			}
		}
	}
}

冒泡排序的时间复杂度是。当排了一趟后数组有序了，时间复杂度就有可能为。所以这个冒泡排序还可以做以下的优化。

void BubbleSort(int* arr, int n) // 冒泡排序
{
	for (int j = 0; j < n; j++)
	{
		int flag = 0;
		for (int i = 1; i < n - j; i++)
		{
			int t = arr[i];
			if (arr[i - 1] > arr[i]) //前一个比后一个大就交换
			{
				Swap(&arr[i - 1], (&arr[i]));
				flag = 1;
			}
		}
		if (flag == 0) break; // 数组遍历一次后没有发生交换，就可以直接退出
	}
}

就算我们排了2遍数组才有序，然后直接退出，那也是可以减少遍历次数的。

2.希尔排序

插入排序其实还可以，插入排序最怕的就是逆序的情况，希尔就对插入排序做了优化。

希尔排序的思想大概就是在插入排序之前，先来一个预排序，期望通过这个预排序让这个数组接近有序。

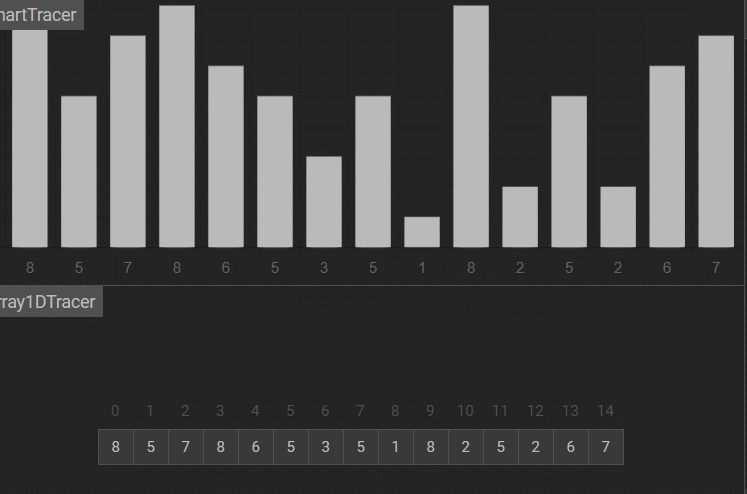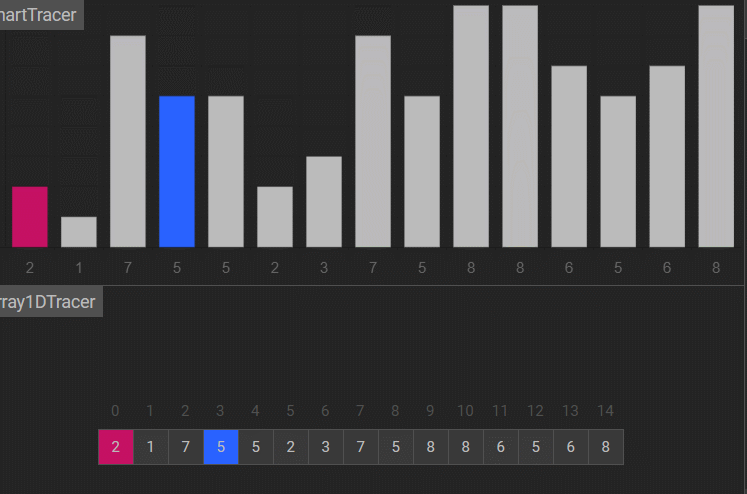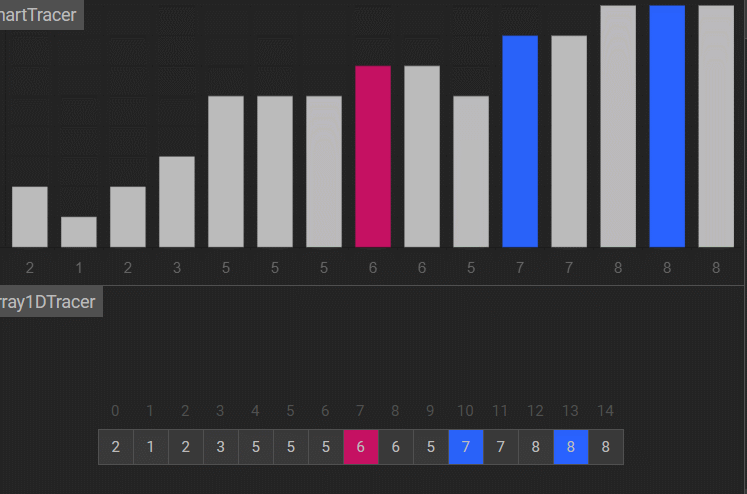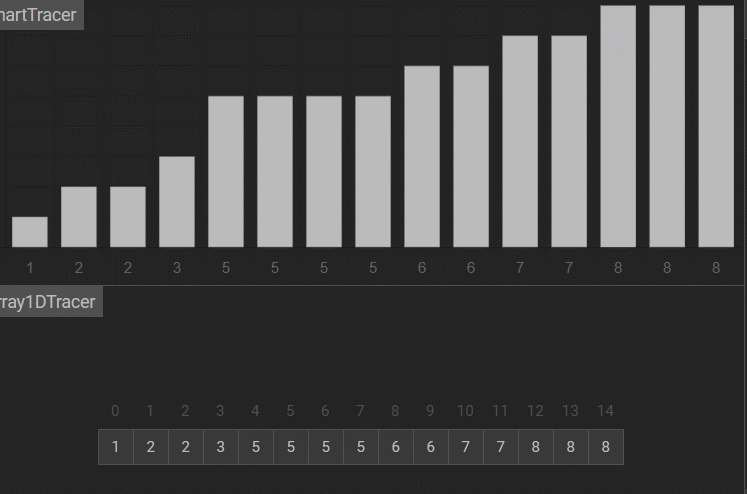
把数组分成gap组，这个gap是多少不确定，这里假设gap为5。5个数为间隔的比，其实也就是把数分成了5组，比如下面的9、4一组，1、8一组，2、6一组，5、3一组，7、5一组。在组内用插入排序的方式排序。

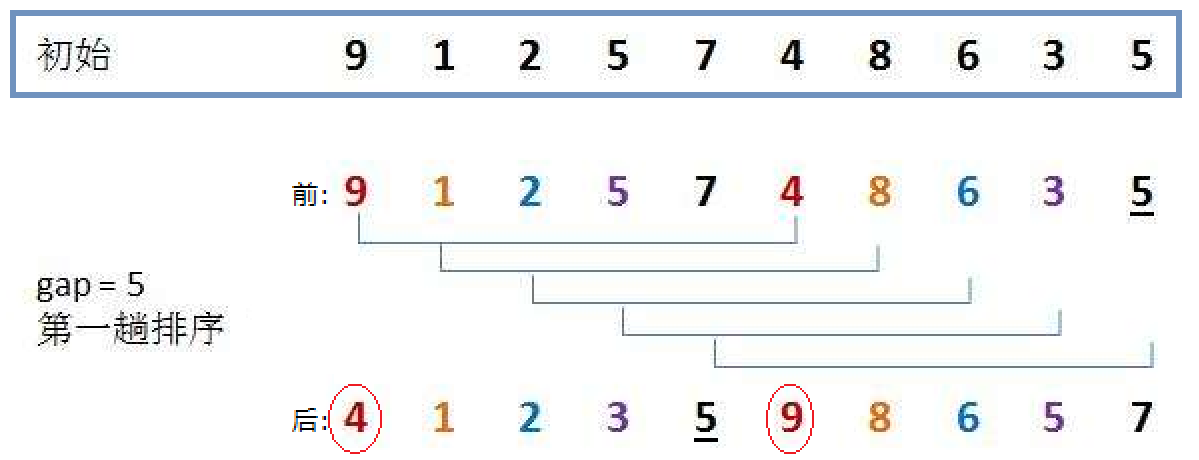
比如说这个9，之前的插入排序要让9一步一步往后走，现在一下就往后跳了5步。预排序之后这个数组就更接近有序了。

我们把第一组，也就是9和4这个排了，组内排序的方法就是希尔排序。

void ShellSort(int* arr, int n) //希尔排序
{
	int gap = 5;
    for (size_t i = 0; i < n - gap; ++i)
    {
	    int end = i;
	    int tmp = a[end + gap];
	    while (end >= 0)
	    {
		    if (tmp < a[end])
		    {
			    a[end + gap] = a[end];
			    end -= gap;
		    }
		    else
		    {
			    break;
		    }
	    }
	    a[end + gap] = tmp;
    }
}

然后我们排第二组的1和8还有后面的所有组，所以这里需要再加上一个循环。

void ShellSort(int* a, int n) //希尔排序
{
	int gap = 5;
	for (int j = 0; j < gap; j++)
	{
		for (size_t i = j; i < n - gap; i += gap)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

当gap为1是，其实就是插入排序，这里我们可以带入一下gap为1的情况，所有的判断条件和代码逻辑其实就是插入排序。

当gap越大，排的越快，但是数组越不接近有序，gap越小，排的速度越慢，但是数组越接近有序。

所以这个gap其实是变化的，不是固定的，可以每次除以任何数比如2、3等来进行变化，有大佬研究过这个gap除以3希尔排序的效果是最好的；

当gap为1时，我们就认为这个数组已经排好了，但是除以3的话gap可能不会等于1，所以gap最好的取值方法就是gap = gap / 3 + 1，完整参考代码如下。

void ShellSort(int* a, int n) //希尔排序
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		//printf("gap=%d: ", gap);
		for (int j = 0; j < gap; j++)
		{
			for (size_t i = j; i < n - gap; i += gap)
			{
				int end = i;
				int tmp = a[end + gap];
				while (end >= 0)
				{
					if (tmp < a[end])
					{
						a[end + gap] = a[end];
						end -= gap;
					}
					else
					{
						break;
					}
				}
				a[end + gap] = tmp;
			}
		}
		//Print(a, n);
	}
}

我们来测试一下。

int main()
{
	int arr[] = { 30,5,12,34,7,26,87,4,39,30,5,12,34,7,26, 1 };
	int n = sizeof(arr) / sizeof(arr[0]);
	Print(arr, n);
	ShellSort(arr, n);
	Print(arr, n);
	return 0;
}

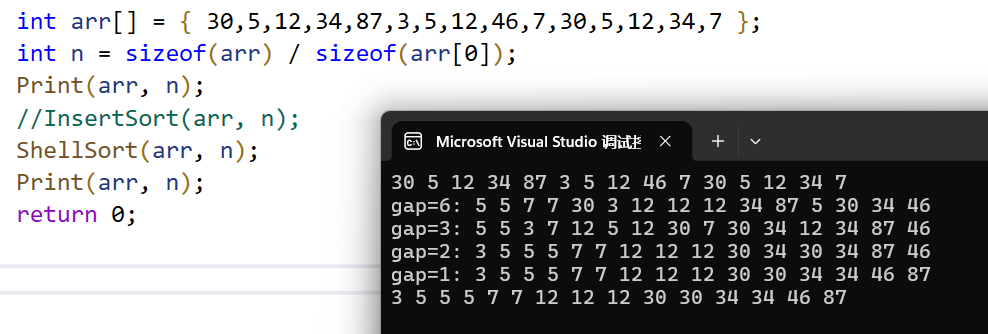
希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，希尔排序的时间复杂度大概是到，没有到。

3.选择排序

先直接看图一下选择排序的效果。

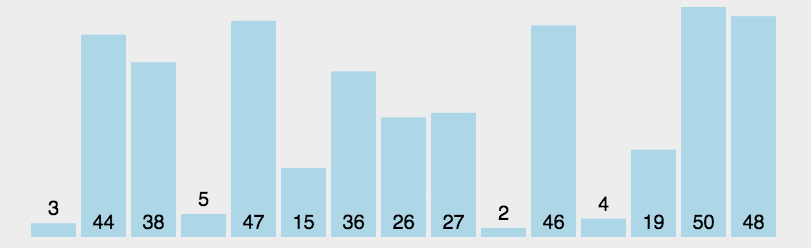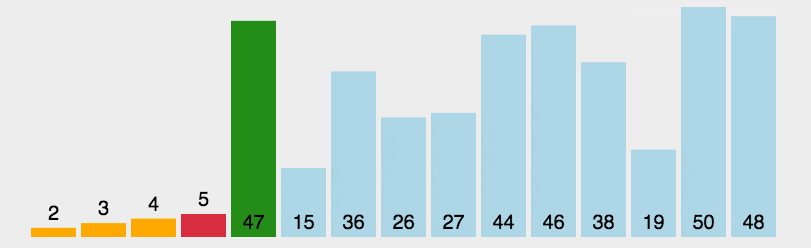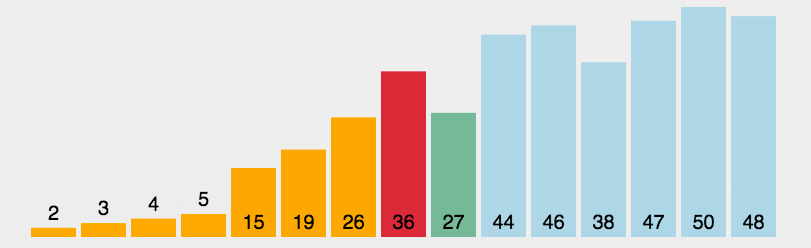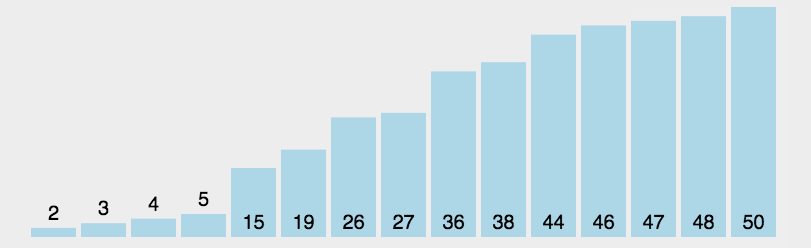
每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完 。
这个选择排序有一个可以优化的点，就是便利的时候我们可以直接 找出最大的和最小的，遍历一遍选出两个数，不一定是只找出某一个，这样会让排序更快。

• 注意这里找数的时候，不是直接覆盖别的数，其实本质就是找最小的数和最大的数的下标。

void SelectSort(int* arr, int n) //选择排序
{
	int left = 0, right = n - 1;
	while(left < right)
	{
		int min_index = left;
		int max_index = right;
		for (int i = left; i <= right; i++)
		{
			if (arr[i] > arr[max_index])
				max_index = i;
			else if (arr[i] < arr[min_index])
				min_index = i;
		}
		Swap(&arr[left], &arr[min_index]);
		Swap(&arr[right], &arr[max_index]);
		left++;
		right--;
	}
}

但是有个特殊情况，用下面的数组为例。

现在是已经找出来了最大数和最小数的下标。

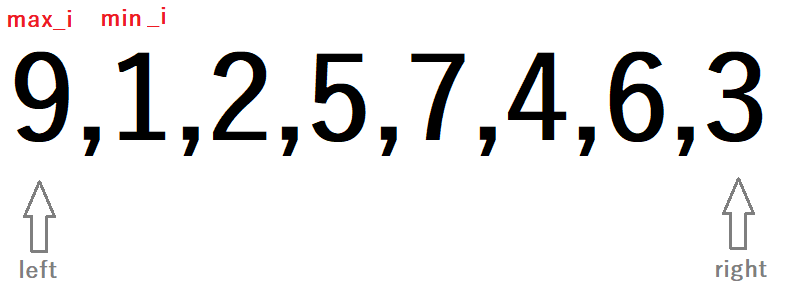
然后最小数放在左边，如下。

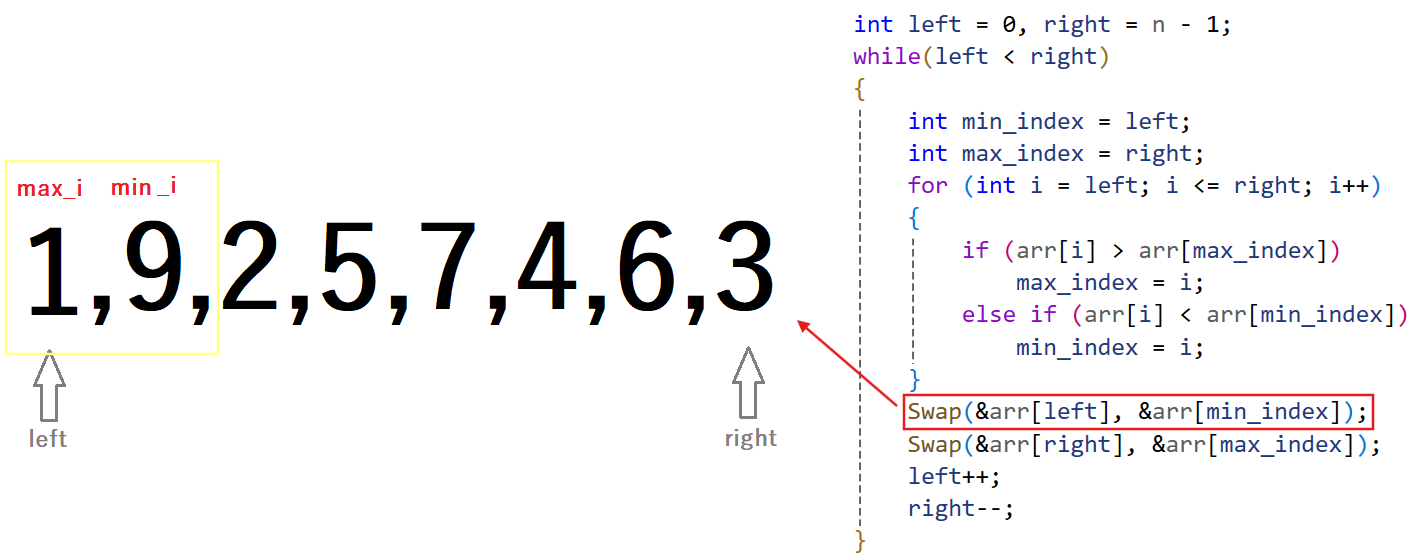
但是此时的最大数就被调换了，会导致最大数不能正确放置。

所以需要在交换最大数的时候更新最大数的下标，如下。

void SelectSort(int* arr, int n) //选择排序
{
	int left = 0, right = n - 1;
	while(left < right)
	{
		int min_index = left;
		int max_index = right;
		for (int i = left; i <= right; i++)
		{
			if (arr[i] > arr[max_index])
				max_index = i;
			else if (arr[i] < arr[min_index])
				min_index = i;
		}
		Swap(&arr[left], &arr[min_index]);
		if (left == max_index) max_index = min_index; //特殊情况下，更新下标
		Swap(&arr[right], &arr[max_index]);
		left++;
		right--;
	}
}

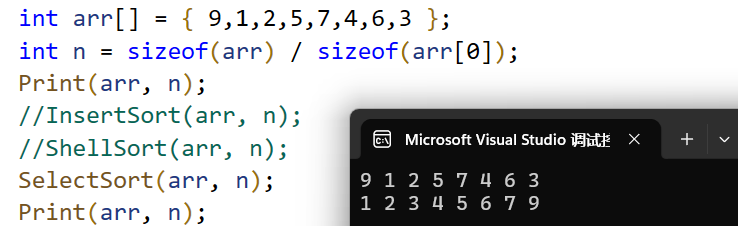
选择排序的时间复杂度是。

4.快速排序

递归实现

Hoare版本

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：

任取待排序元素序列中的某元素作为基准值**，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止**。

如下图。

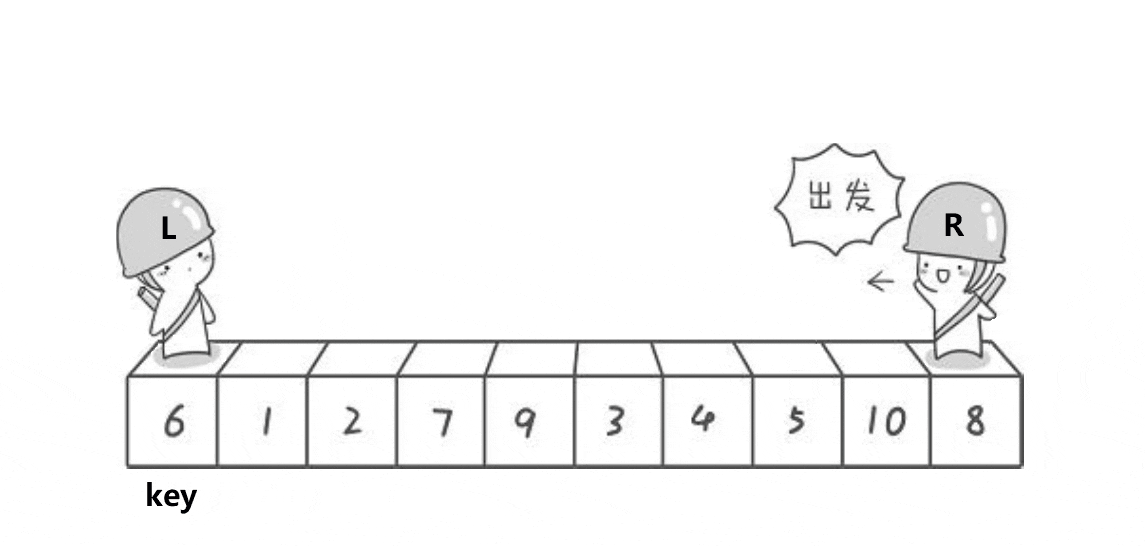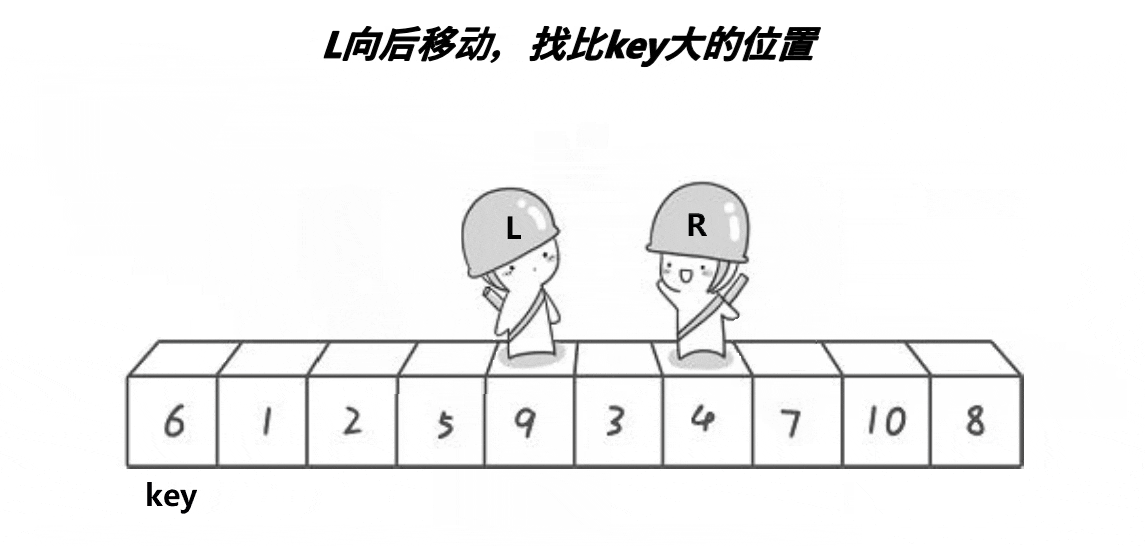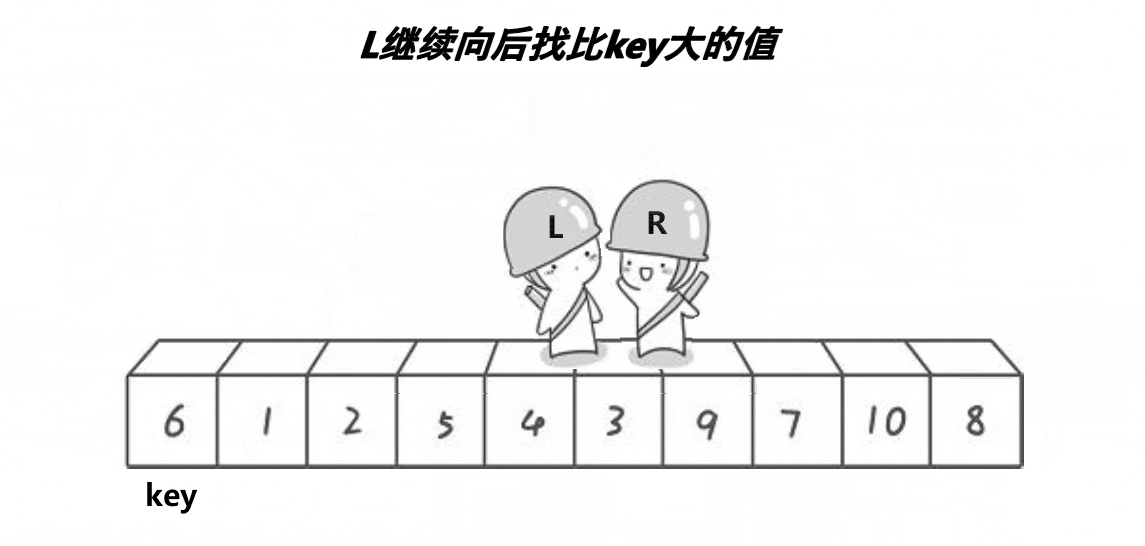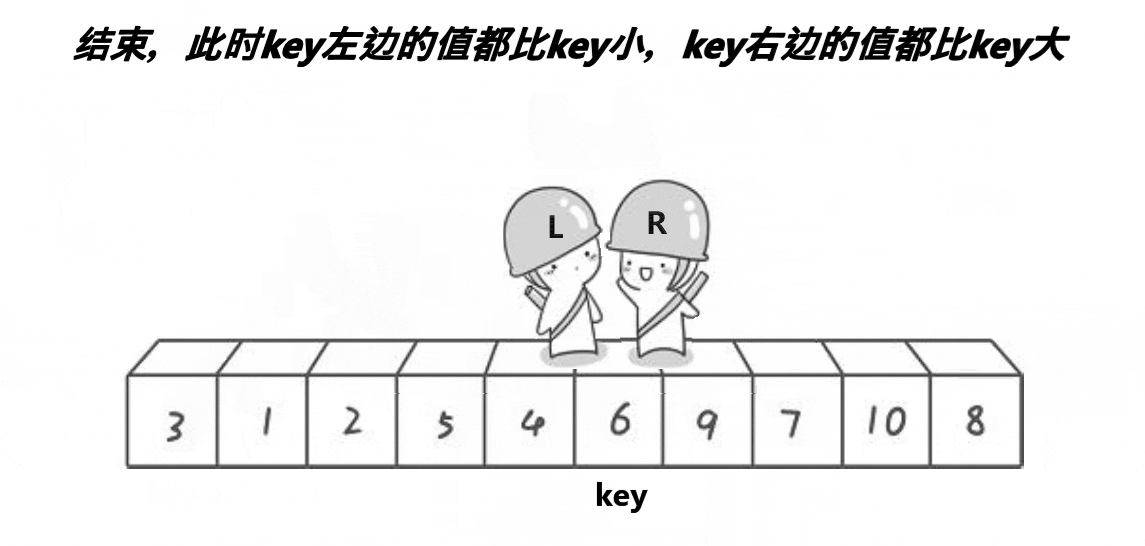
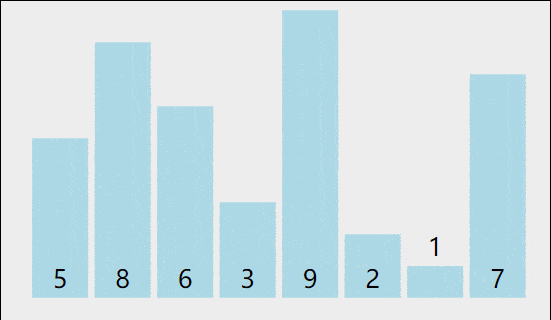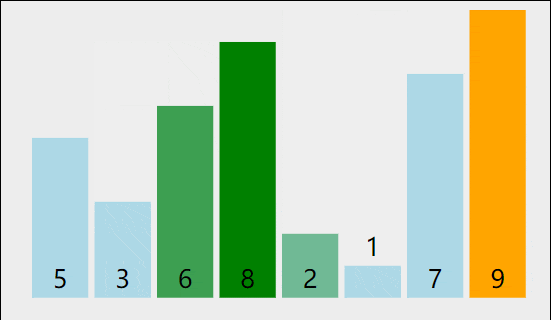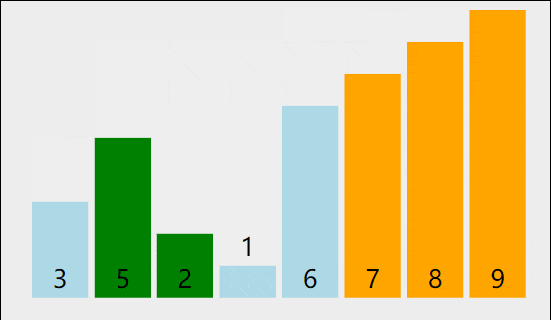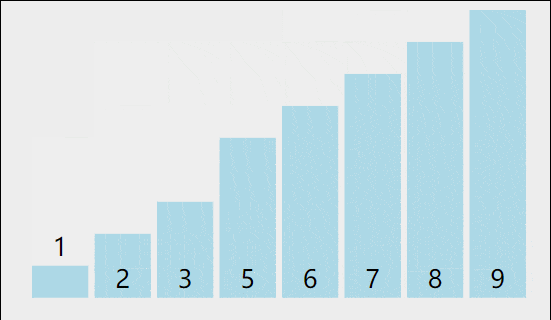
key设在最左边，右边就找比key小的数，左 边就找比key大的数，然后交换两个数的位置，再继续找，直到L和R相遇，相遇的位置的数一定比key小（前提是右边先走）。

如果让左边先走，相遇位置的值一定比key大，此时我们的key就要设在右边。

图中就将6排好了

，因为比6小的都在左边，比6大的都在右边，不管6的左右是否有序，6反正确定位置了，比6小或大的有几个数肯定是确定的。

此时如果6的左边有序，右边也有序的话，是不是就排好了。怎么让左边有序右边也有序？同样的道理。

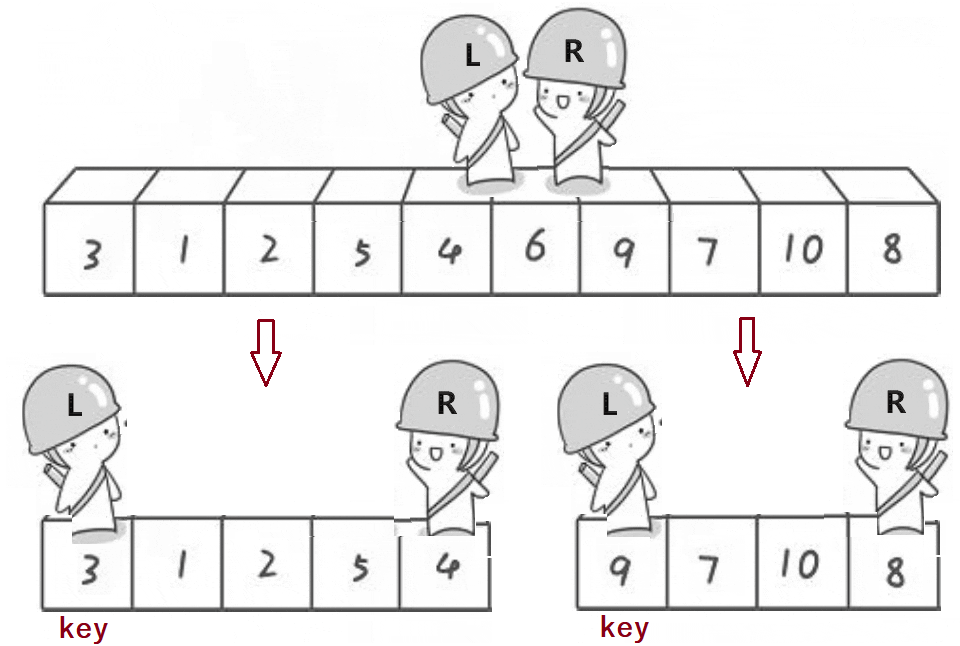
一直往后往后，其实就是一个二叉树。

先实现一次的排列，这里实现的是key设在左边，必须让右边先走的逻辑。

void QuickSort(int* arr, int begin, int end)
{
	int key = arr[begin];
	int left = begin, right = end;
	while (left < right)
	{
		while (left < right && arr[right] >= key) //右边找小，不小就一直找
		{
			right--;
		}
		while (left < right && arr[left] <= key) //左边找大，不大就一直找
		{
			left++;
		}
		Swap(&arr[left], &arr[right]); //交换
	}
	//将key与相遇位置的值交换
	arr[begin] = arr[left]; //此时left和right是一样的
	arr[left] = key;

}

排好了之后就是递归式的把右边和左边都排好，当这个区间只有一个数的时候，这个区间就绝对有序，所以递归结束的条件是其实就是begin >= end的情况。

排好的这个数不再参与排序。

void QuickSort(int* arr, int begin, int end)
{
	if (begin >= end) // 递归结束条件
		return; 
	int key = arr[begin];
	int left = begin, right = end;
	while (left < right)
	{
		while (left < right && arr[right] >= key) //右边找小，不小就一直找
		{
			right--;
		}
		while (left < right && arr[left] <= key) //左边找大，不大就一直找
		{
			left++;
		}
		Swap(&arr[left], &arr[right]); //交换
	}
	//将key与相遇位置的值交换
	arr[begin] = arr[left]; //此时left和right是一样的
	arr[left] = key;

	QuickSort(arr, begin, left - 1); //排左序列
	QuickSort(arr, left + 1, end); //排右序列
}

快排的时间复杂度其实是。

但是当前实现方式会有如下问题：

• 当数组有序的时候，这个排序是非常吃力的，因为key永远是最小的那个数，导致right一直往左走，left和right相遇后，其实就是在key的位置相遇，然后自己和自己交换一下，左区间触发递归结束条件，直接返回，右区间长度为n-1，重复上述过程，左区间没有，右区间长度为n-2...所以在这种情况下快排的时间复杂度为，效率明显降低。

• 并且，如果数太多，导致递归的深度太深，就会有栈溢出的风险。

避免有序情况下效率退化，我们在选key的时候就不能固定一个位置选。

• 这个key可以弄成随机数选key，但是这个方法还是有一点不太靠谱。
• 三数取中：最左边的数，最右边的数，中间的数，选择这三个数当中，不是最大的数也不是最小的数的那个数，为了保持之前的代码逻辑不变，我们找到不是最大也不是最小的那个数之后，还是放到最左边，用之前的逻辑。这样在有序的情况下，key的位置还是在最左边，但做左边的这个值不是最小值。

小区间优化：

• 当区间内的数比较少的时候，其实就不需要用递归了，一点点数用递归代价太大，我们可以在小区间内换一个排序方式，插入排序就是一个很好的选择。

void QuickSort(int* arr, int begin, int end)
{
	if (begin >= end) // 递归结束条件
		return; 
	if (end - begin <= 10)
	{
		//注意这里不是arr，要加上begin才是真正要排的起始位置
		InsertSort(arr + begin, end - begin + 1); 
	}
	else
	{
		int key = arr[begin];
		int left = begin, right = end;
		while (left < right)
		{
			while (left < right && arr[right] >= key) //右边找小，不小就一直找
			{
				right--;
			}
			while (left < right && arr[left] <= key) //左边找大，不大就一直找
			{
				left++;
			}
			Swap(&arr[left], &arr[right]); //交换
		}
		//将key与相遇位置的值交换
		arr[begin] = arr[left]; //此时left和right是一样的
		arr[left] = key;

		QuickSort(arr, begin, left - 1); //排左序列
		QuickSort(arr, left + 1, end); //排右序列
	}
}

前面的版本叫hoare****版本，其实还有一个版本叫挖坑法。挖坑法就不是实现了。

挖坑法

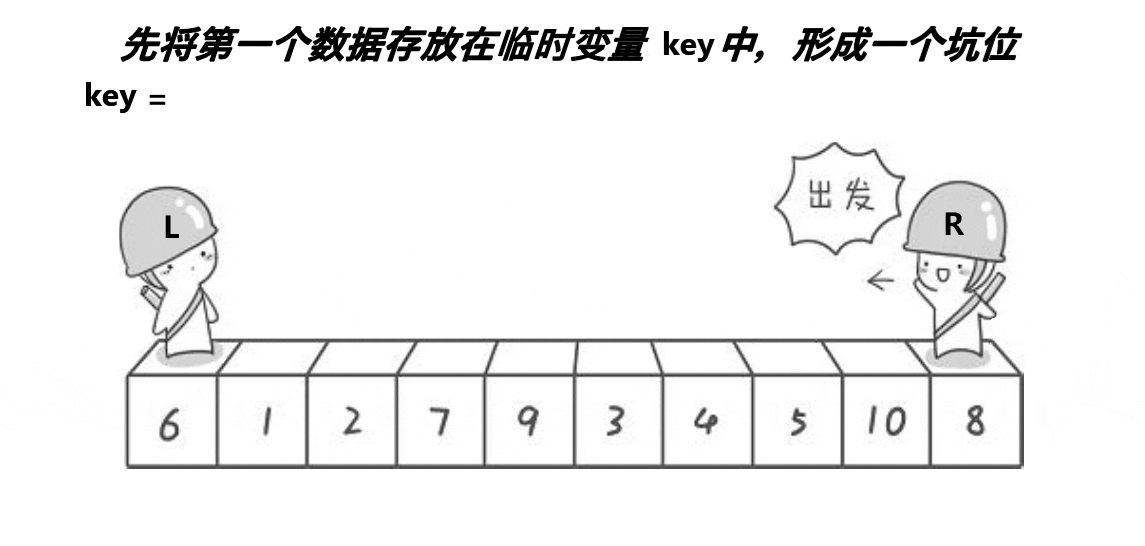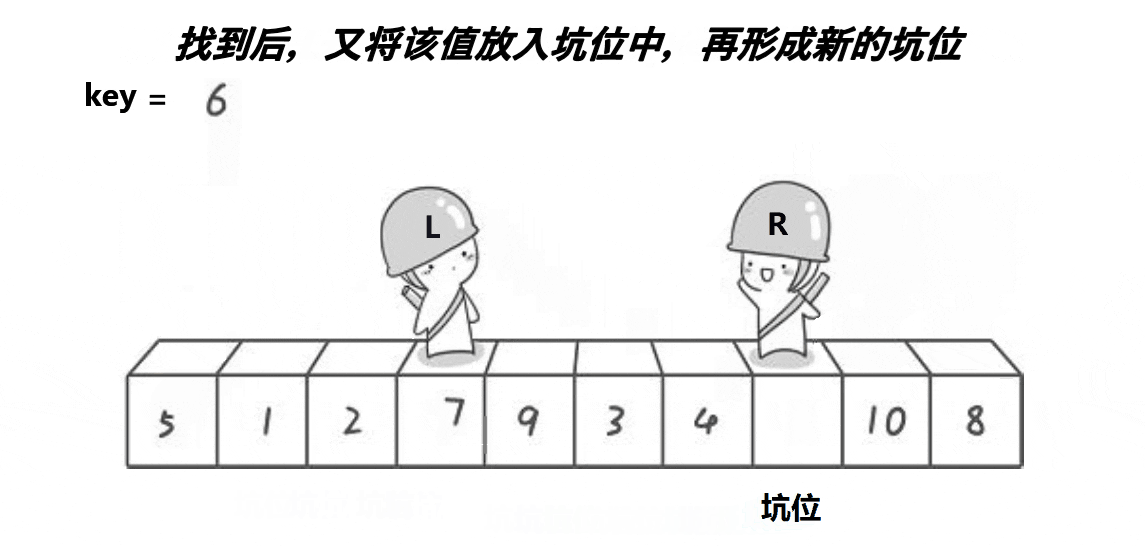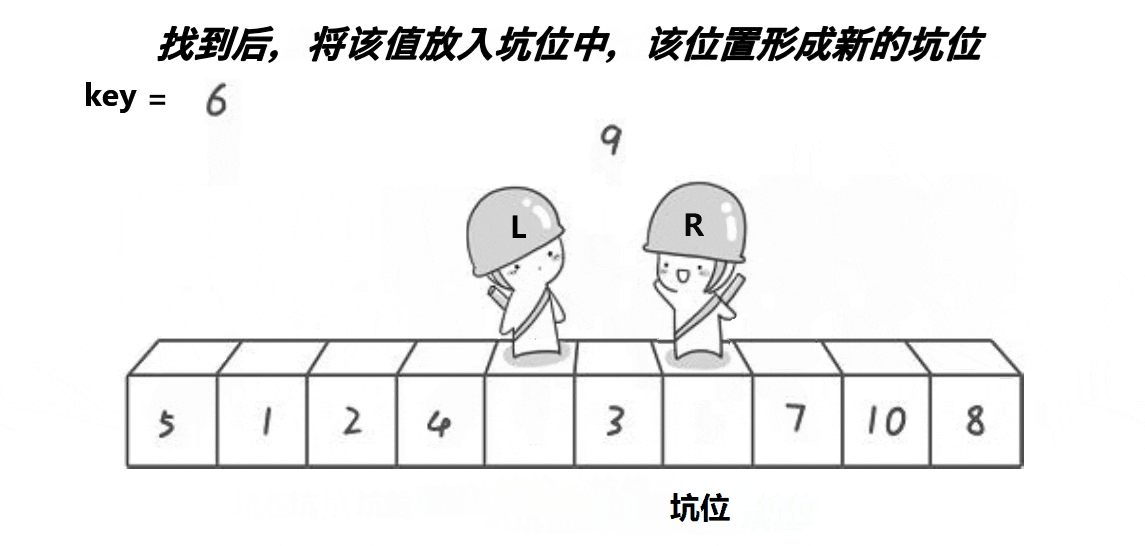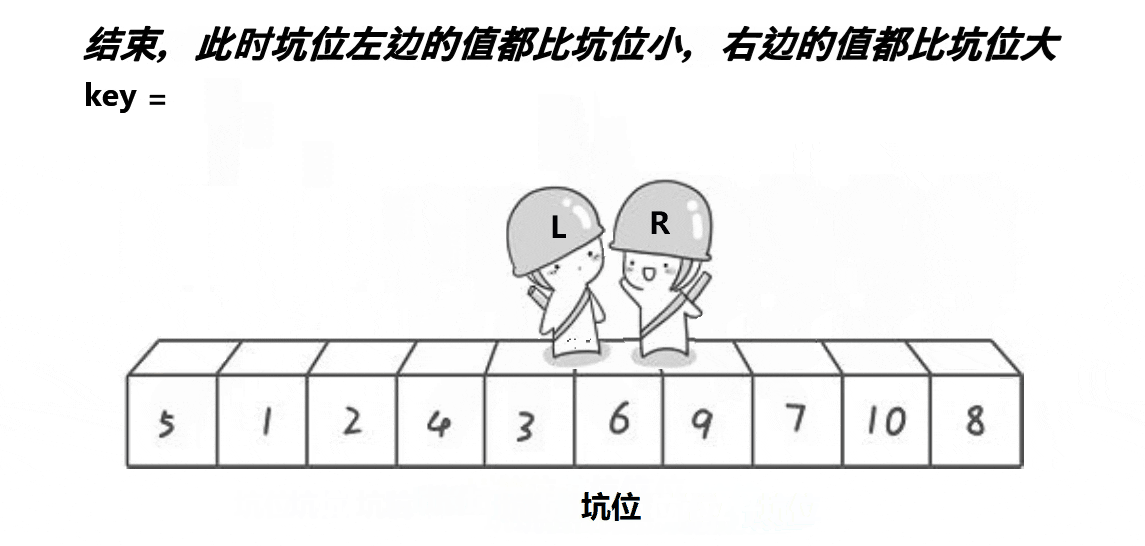
右边找比key小的数，放到坑里，这个数的位置成为新的坑，左边找比key大的数，放到坑里，这个数的位置变成新的坑，直到他们相遇。

效率上没有任何变化，但是逻辑上可能更容易理解，就比如为什么左边取为key就要让右边先走，相遇位置怎么就一定比key小...挖坑法就是直接放到坑里。

前后指针法

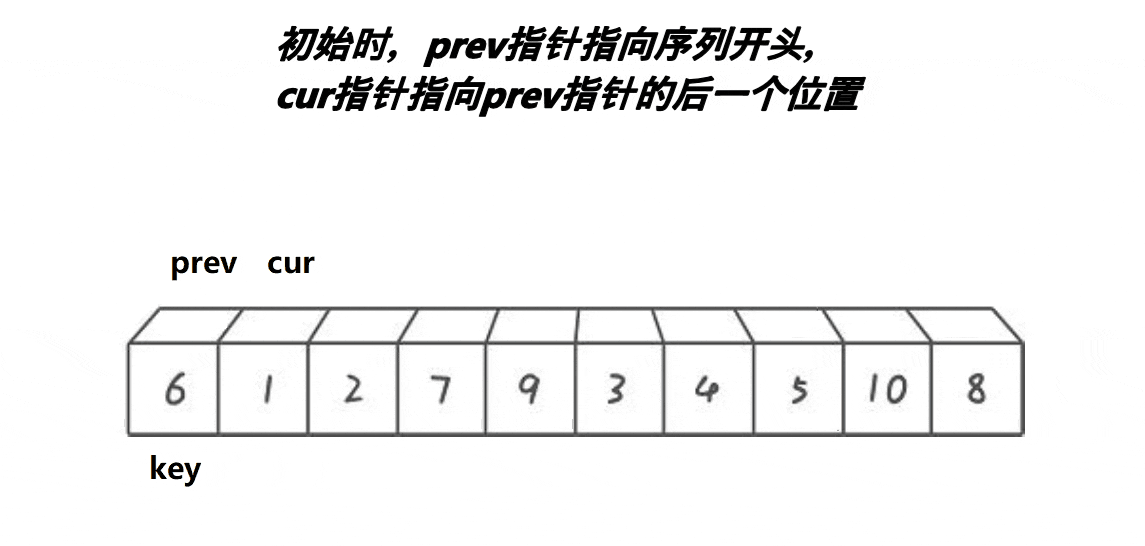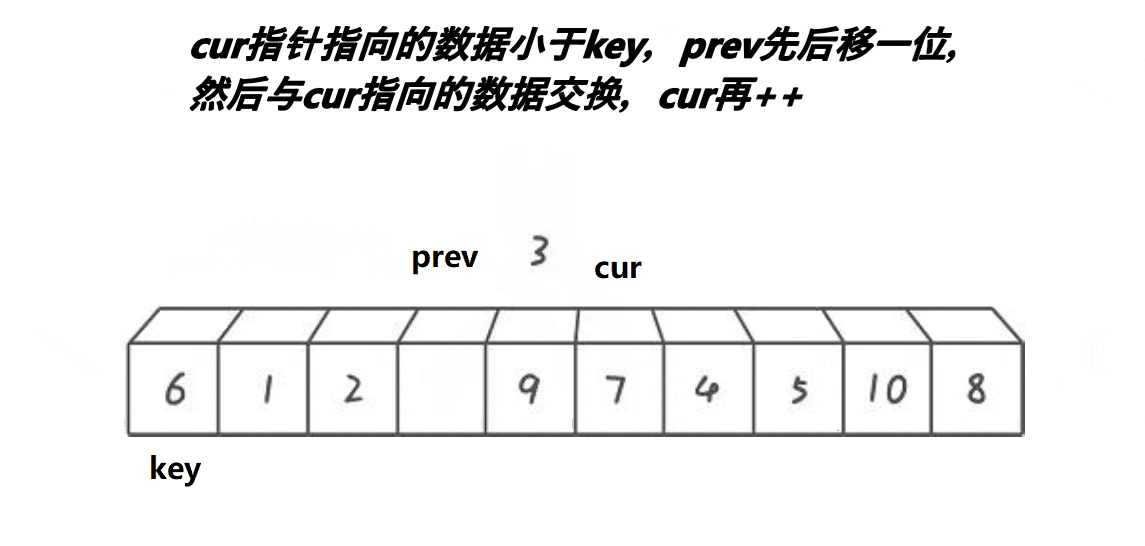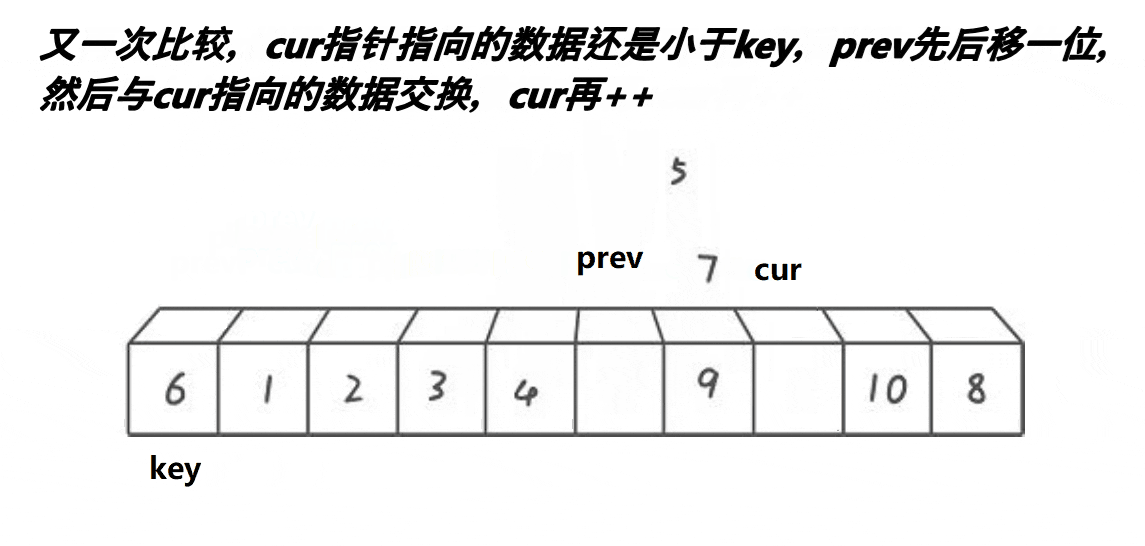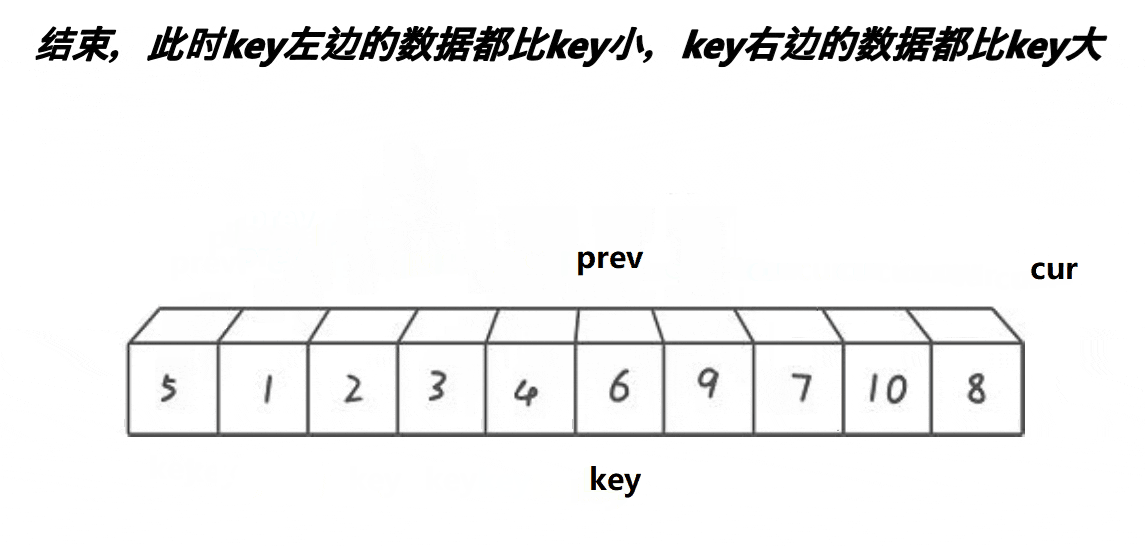
目的还是为了让左边的数比key小，右边的数比key大。cur找比key小的值，找到比key小的值之后，先让prev加1，然后交换cur和prev位置的数，遇到比key大的数就继续往后找；如果prev和cur相等，就是自己和自己交换，不用管；prev和cur中间的数都是比key大的数，让这些数像翻跟头一样往右边挪。

代码实现如下：

int Sort_Pointers(int* arr, int begin, int end) //前后指针版
{
	int prev = begin, cur = prev + 1;
	while (cur <= end)
	{
		if (arr[cur] < arr[begin])
		{
			++prev;
			if (prev != cur)
				Swap(&arr[prev], &arr[cur]);
		}
		cur++;
	}
	return prev; //prev就是key要交换的值所在的位置
}

void QuickSort(int* arr, int begin, int end)
{
	if (begin >= end) // 递归结束条件
		return;
	//单趟逻辑封装成函数，让单趟逻辑有多种方式可选
	//int swap_i = HoareSort_Part(arr, begin, end); //hoare版
	int swap_i = Sort_Pointers(arr, begin, end); //前后指针版
	Swap(&arr[begin], &arr[swap_i]);

	QuickSort(arr, begin, swap_i - 1); //排左序列
	QuickSort(arr, swap_i + 1, end); //排右序列
}

//封装的hoare版本接口如下
int HoareSort_Part(int* arr, int begin, int end) //hoare版本
{
	int left = begin, right = end;
	while (left < right)
	{
		while (left < right && arr[right] >= arr[begin]) //右边找小，不小就一直找
		{
			right--;
		}
		while (left < right && arr[left] <= arr[begin]) //左边找大，不大就一直找
		{
			left++;
		}
		if (left < right)
			Swap(&arr[left], &arr[right]); //交换
	}
	return left;
}

验证是没问题的。

快排的时间复杂度是。

非递归实现

非递归我们可以借助数据结构栈或者队列，如果使用栈，就是深度优先遍历，如果使用队列，就是广度优先遍历。

这里详细讲解借助栈实现非递归版的快排。

核心逻辑：将要排序的区间入栈，循环每走一次，就取栈区间，进行单趟排序，然后左右子区间在将要排序的区间入栈...

引入之前实现的栈，详细讲解在：【数据结构】栈的概念、结构和实现详解

参考代码：

void QuickSort_Non_R(int* arr, int begin, int end) //快排非递归实现
{
	ST st;
	STInit(&st);
	STPush(&st, begin); //先入区间左边界
	STPush(&st, end);   //再入区间右边界
	while (!STEmpty(&st))
	{
		end = STTopDate(&st);
		STPop(&st);
		begin = STTopDate(&st);
		STPop(&st);

		if (end - begin <= 1)
			continue;
		int div = HoareSort_Part(arr, begin, end);
		Swap(&arr[begin], &arr[div]);

		// 以基准值为分割点，形成左右两部分：[left, div) 和 [div+1, right)
		STPush(&st, div + 1);
		STPush(&st, end);

		STPush(&st, begin);
		STPush(&st, div);
	}
	STDestroy(&st);
}

5.归并排序

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：

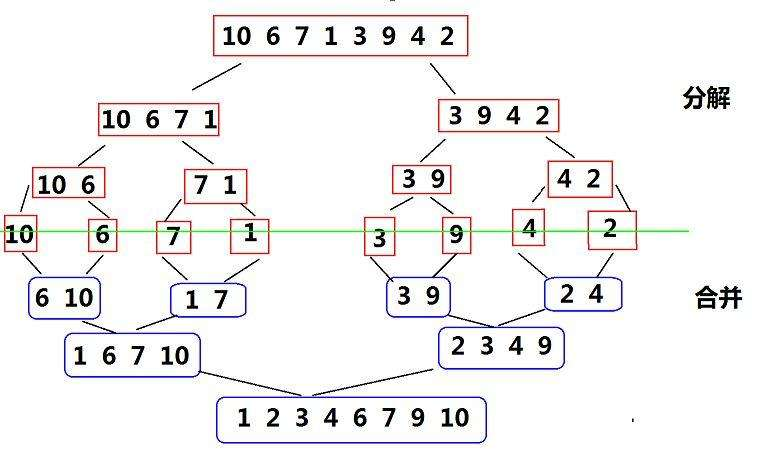
下面是动图：

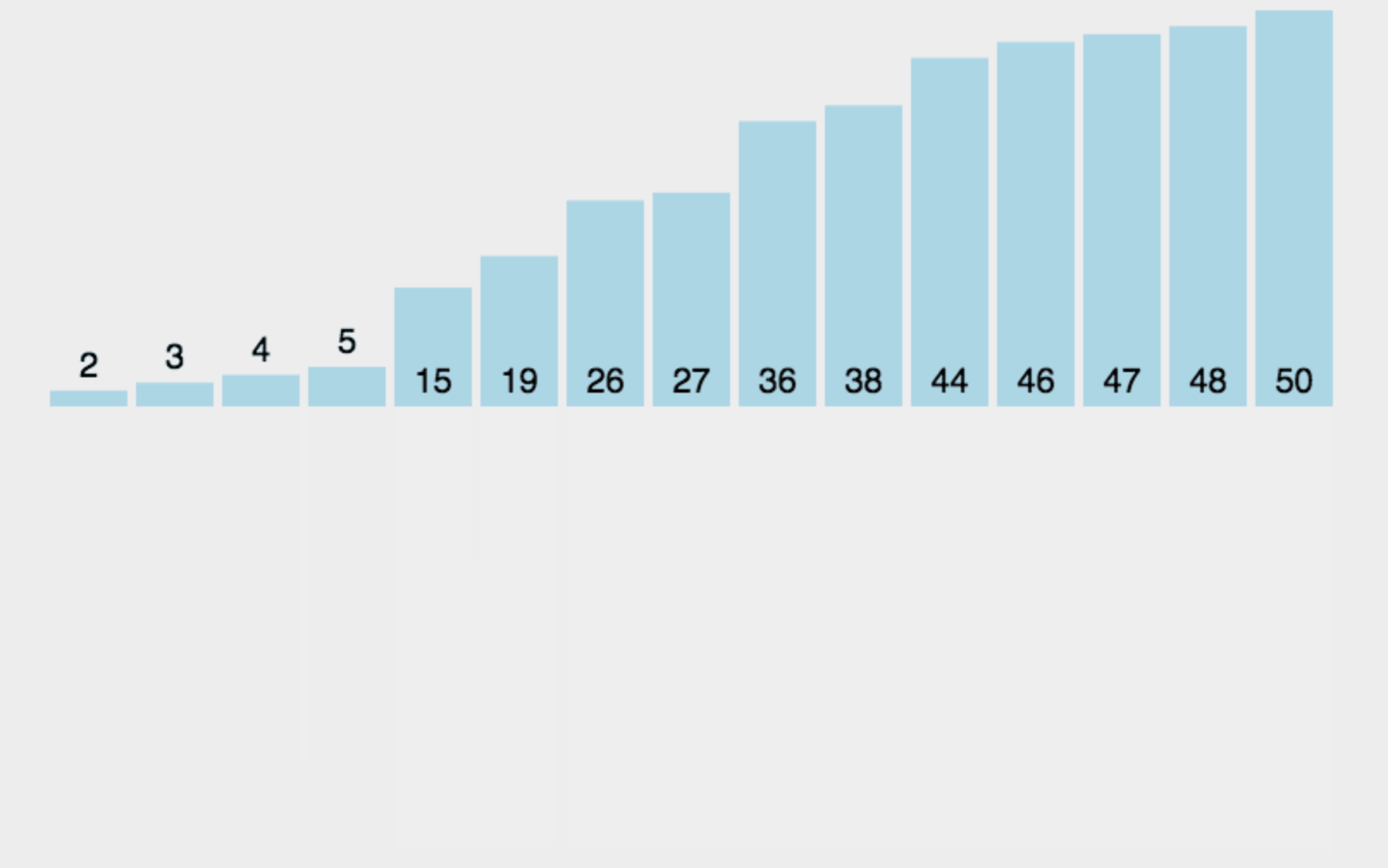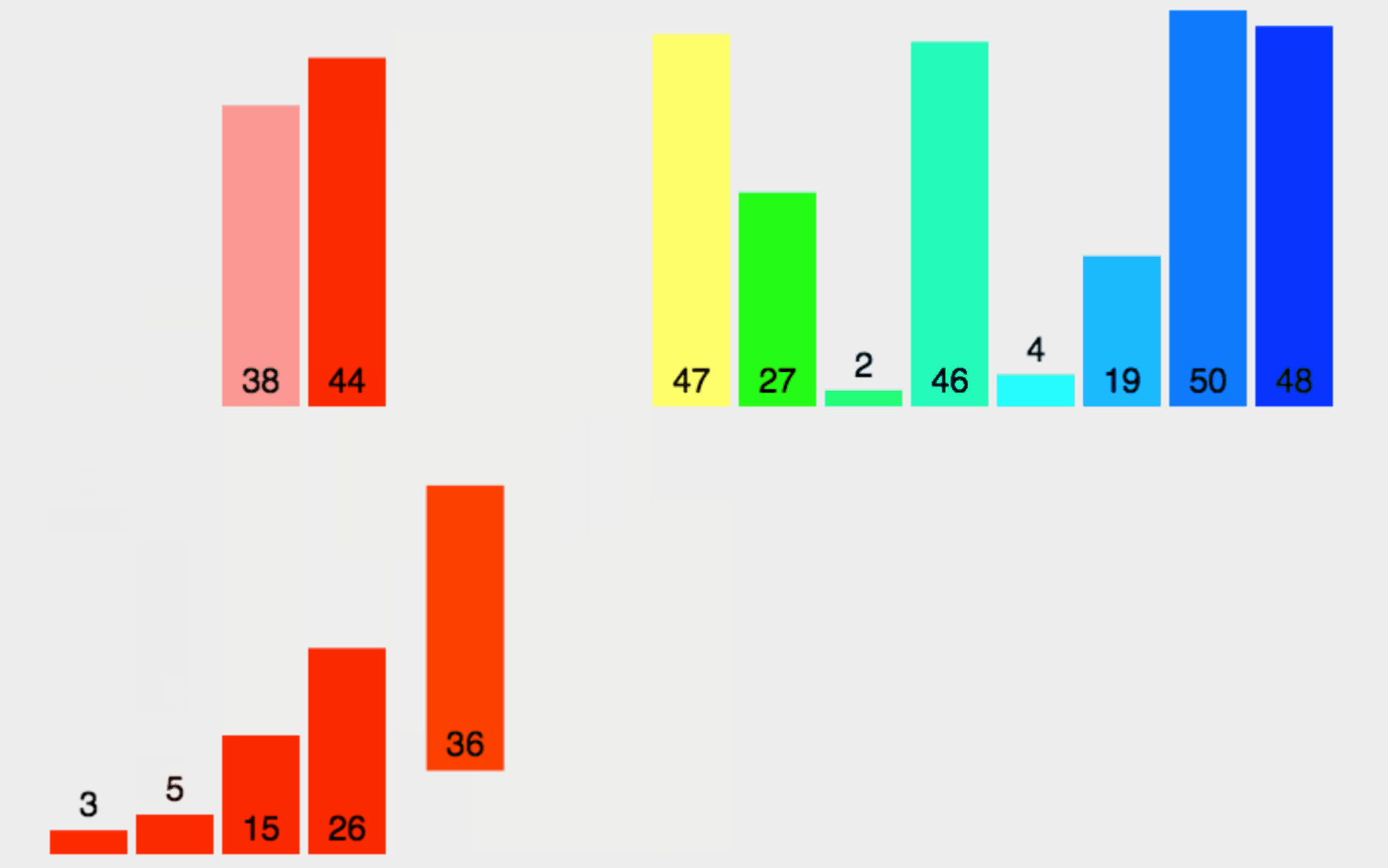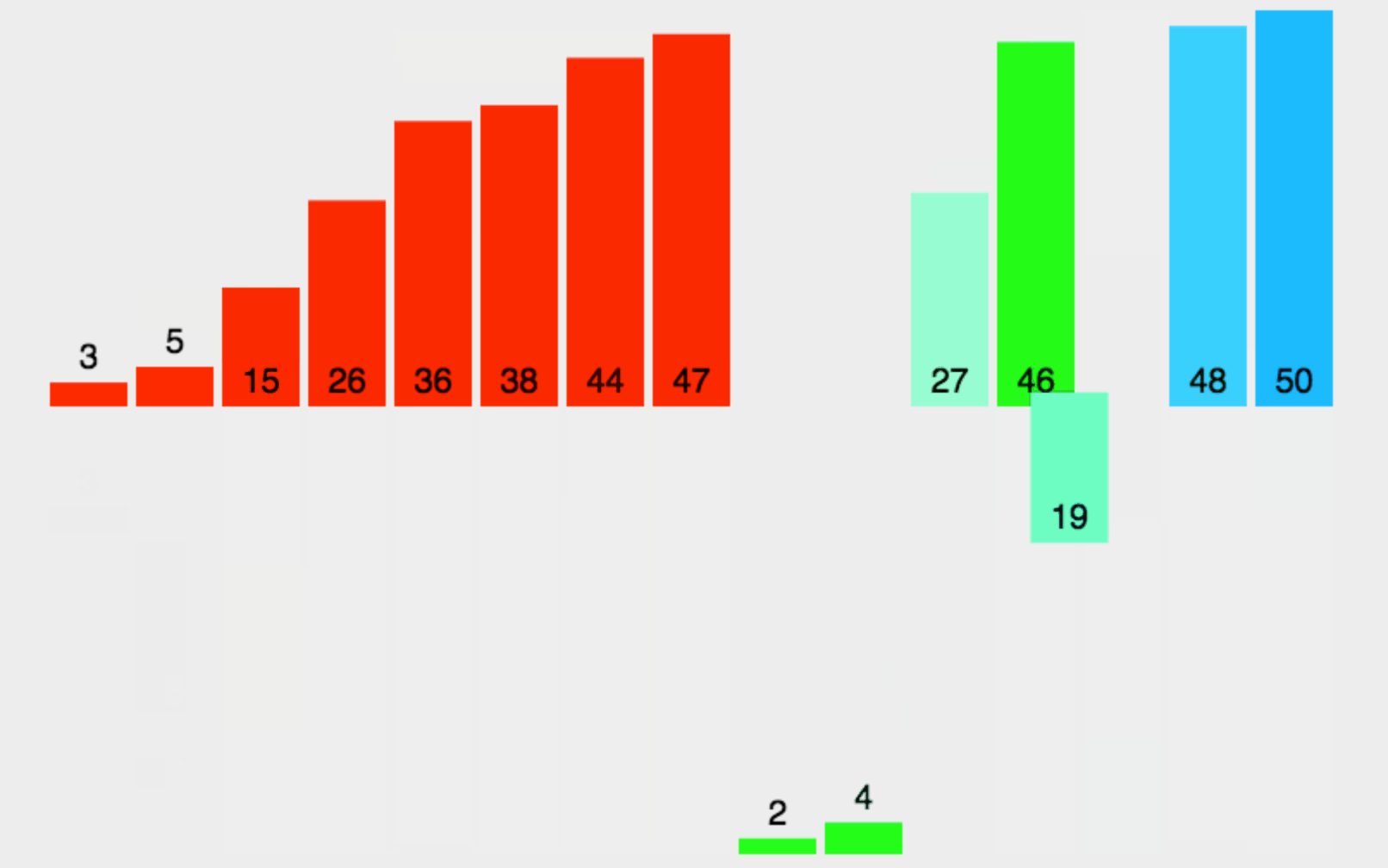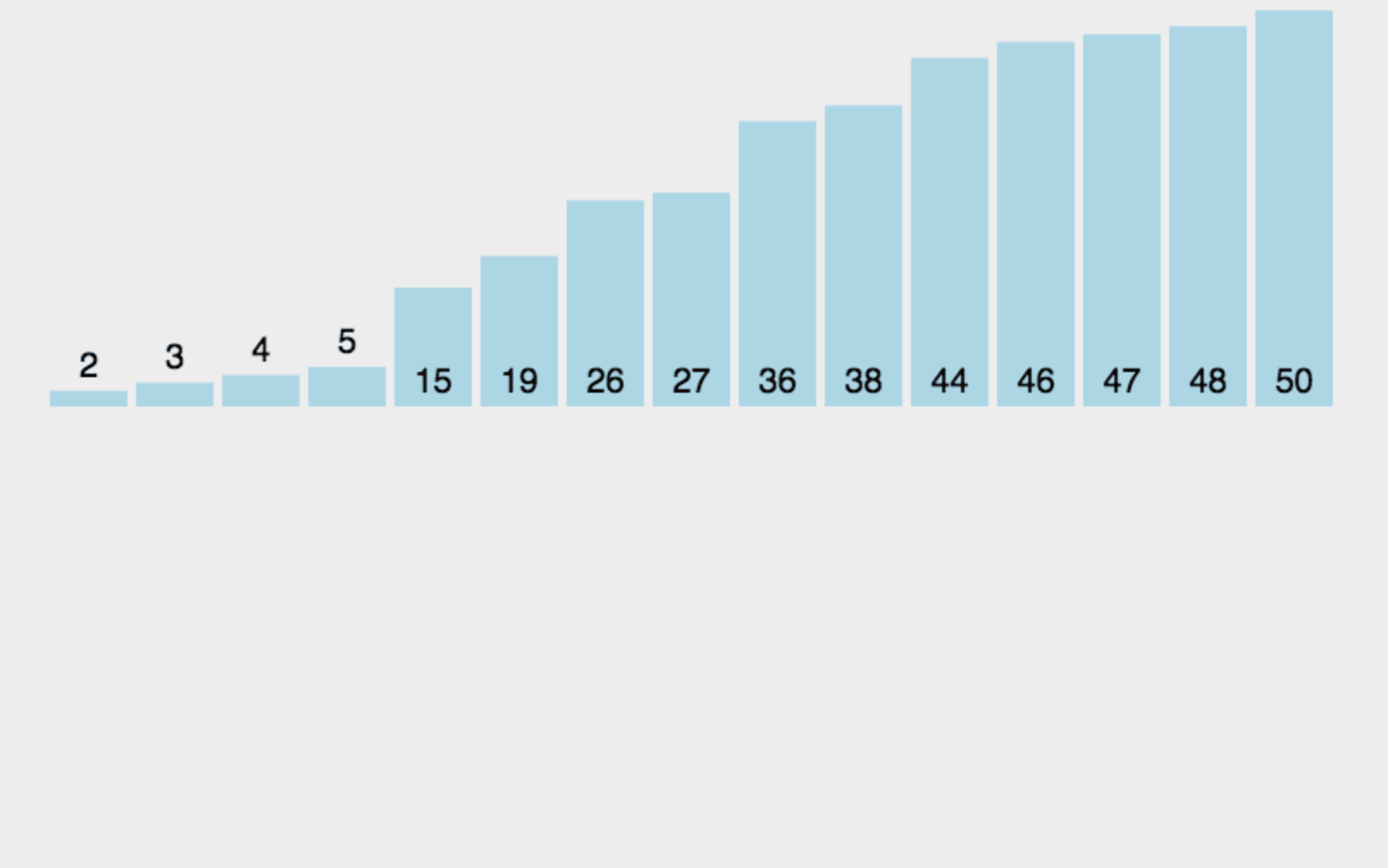
如果说把快排看成前序，这个归并排序就是一个后序。

拿一个部分举例。

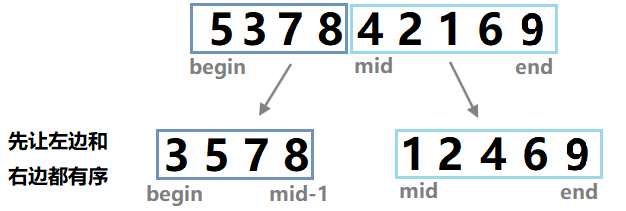
对排序好的数组再合并起来排序，用双指针。

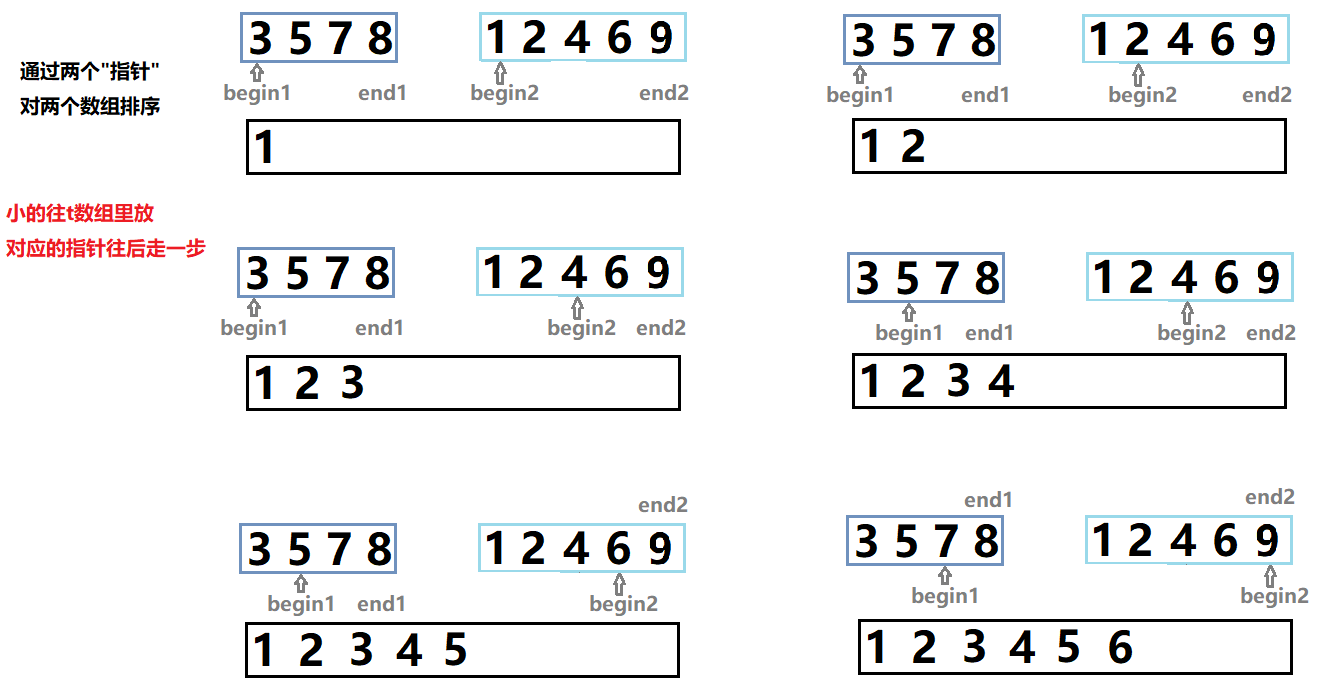
排完了之后还要拷贝进原数组，因为我们是在t数组里排的。

参考代码如下：

void _MergeSort(int *a, int *t, int begin, int end)
{
	if (begin >= end) return; //递归退出条件，只有一个数的时候
	int mid = begin + (end - begin) / 2;
	_MergeSort(a, t, begin, mid); //让左区间有序
	_MergeSort(a, t, mid+1, end); //让右区间有序
	//归并
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			t[i++] = a[begin1++];
		}
		else
		{
			t[i++] = a[begin2++];
		}
	}
	while (begin1 <= end1) //如果左区间没排完继续排
	{
		t[i++]= a[begin1++];
	}
	while (begin2 <= end2) //如果右区间没排完继续排
	{
		t[i++] = a[begin2++];
	}
	//往原数组拷贝
	memcpy(a + begin, t + begin, sizeof(int) * (end - begin + 1));//起始位置要加begin
}

void MergeSort(int* a, int n) //归并排序
{
	int* t = (int*)malloc(sizeof(int) * n); //需要一个临时空间存储排好的数
	if (t == NULL)
	{
		perror("malloc fail");
		return;
	}
	_MergeSort(a, t, 0, n - 1); 
	free(t);
	t = NULL;
}

测试一下。

int main()
{
	int arr[] = { 30,5,12,34,87,3,5,12,46,7,30,5,12,34,7,1 };
	int n = sizeof(arr) / sizeof(arr[0]);
	Print(arr, n);
	MergeSort(arr, n); //归并
	Print(arr, n);
	return 0;
}

归并排序的时间复杂度是；空间复杂度是，因为它额外开了一个数组t。

6.计数排序

这个排序不是比较数的大小，而是比较数出现的次数。

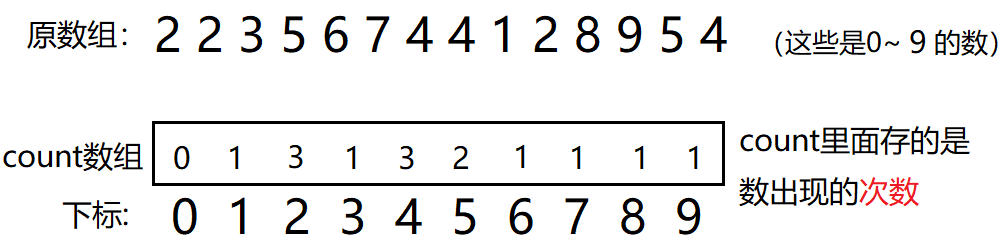
统计完了之后，直接覆盖式的写到原数组，出现几次就写几遍，出现0次的直接跳过。

本质就是利用count数组的自然序号排序。

但是如果数据是100、101、102、103...109那么从0到99的空间不就浪费了。

这个时候就可以按范围开空间，比如最大的数是109，最小的数是100，就开109-100=9个空间，这个就叫相对映射，图里面的就是绝对映射。

参考代码如下：

void CountSort(int* a, int n) //计数排序
{
	int min = a[0], max = a[n - 1];
	for (int i = 1; i < n; i++)
	{
		if (min > a[i]) min = a[i]; //选出最小值
		if (max < a[i]) max = a[i]; //选出最大值
	}
	int range = max - min + 1; //给出范围
	int* count = (int*)calloc(range, sizeof(int)); //开空间，count数组
	if (count == NULL)
	{
		perror("malloc fail");
		return;
	}
	//统计次数
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++; //要减min，比如105减去100才是对应5下标
	}
	//排序
	for (int i = 0, j = 0; i < range; i++)
	{
		while (count[i]--) //个数为0的不会进循环
		{
			a[j++] = i + min; //j是原数组下标，i是count数组下标，
		}
	}
	free(count);
	count = NULL;
}

测试一下。

int main()
{
	int arr[] = { 30,5,12,34,87,3,5,12,46,7,30,5,12,34,7,1 };
	int n = sizeof(arr) / sizeof(arr[0]);
	Print(arr, n);
	CountSort(arr, n);
	Print(arr, n);
	return 0;
}

负数也可以排，就是因为我们做了相对映射。

这个计数排序只适合整数或者数的范围比较集中的。

归并排序的时间复杂度是；空间复杂度是，因为它额外开了一个数组count。

7.总结

堆排之前介绍过，详细讲解在：【数据结构】堆的概念、结构、模拟实现以及应用

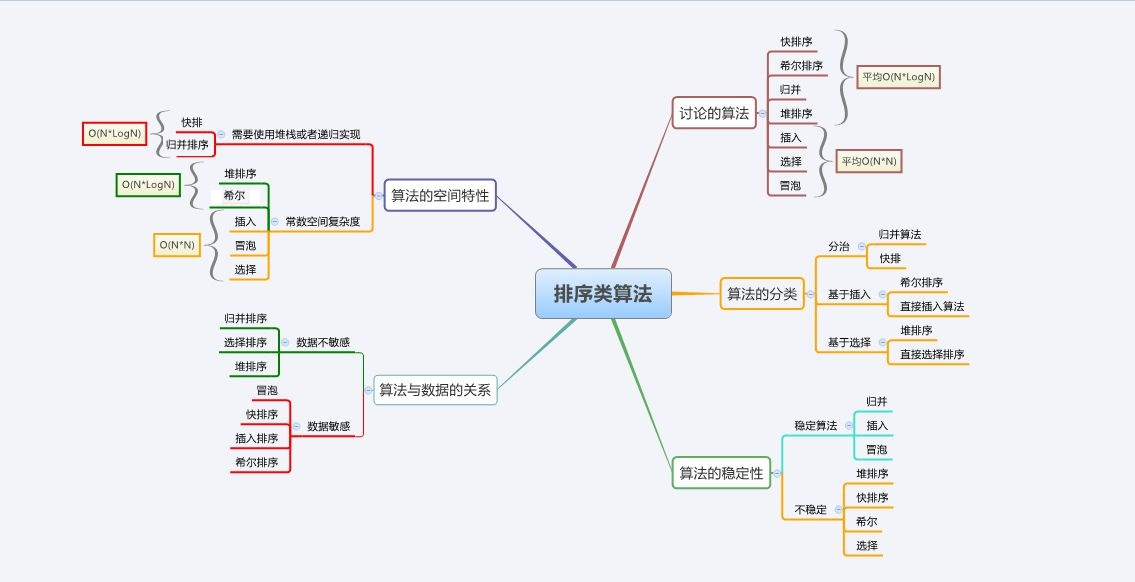
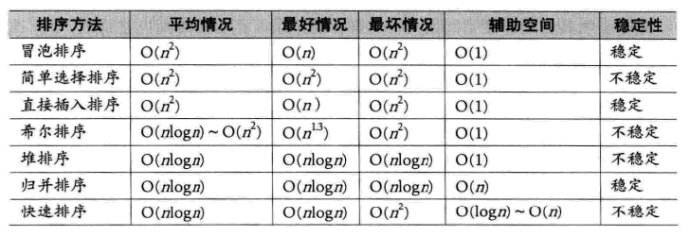
稳定性是指，相同的值，排序后与排序前的相对位置是否容易发生改变。

注意选择排序是不稳定的。快排的空间复杂度是。

本次分享就到这里，我们下篇见~