1 二叉树中序遍历
递归,如同俄罗斯套娃(哈哈哈)。
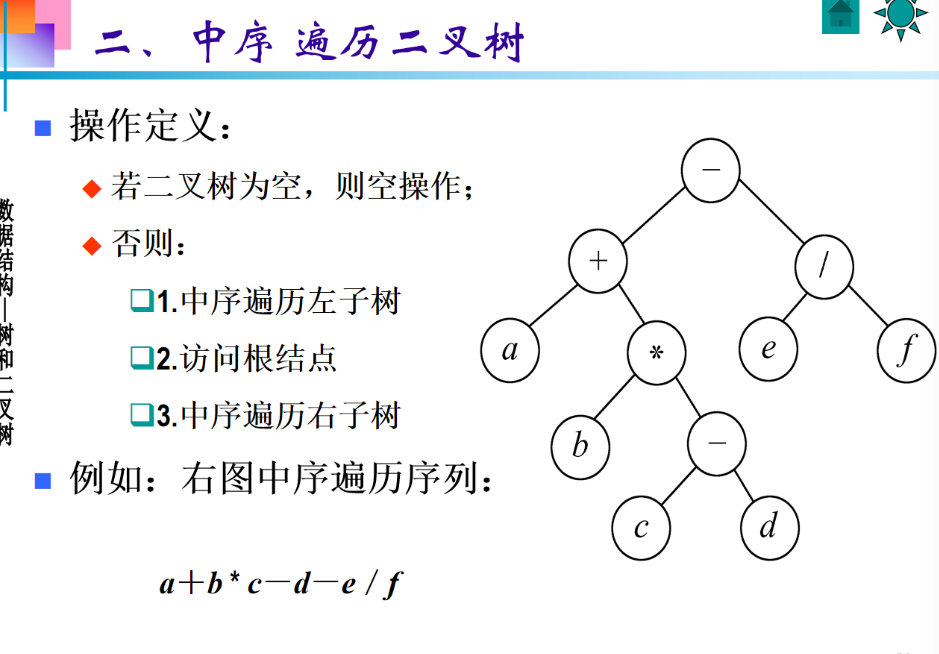
中序遍历是左 - 根 -右 ,从宏观上看,整个树从根节点来看,访问完整个左子树,打印,然后访问右子树,打印。
但是递归的视角来看,整个左子树,又可以当作一个新的树,左子树的第一个结点当作新的根节点(暂且这么表述),在这个新的根节点又开始处理左 - 根 - 右。
俄罗斯套娃的核心就是 "大娃里套中娃,中娃里套小娃,小娃里还有更小的娃",递归遍历二叉树完全就是这个逻辑 ------每一层子树都是一个 "新的套娃",都要遵循 "左→根→右" 的同一规则,直到摸到最里面的 "最小娃"(叶子节点),才会一层层退出来。
遍历历程
步骤 1:拆分二叉树的结构
先把这棵树拆成几个子树,方便逐层分析:
- 最底层子树:以
*为根,左子树是b,右子树是-(根为-,左c、右d) - 中间层子树:以
+为根,左子树是a,右子树是上面的*子树 - 整棵树的根:以
-为根,左子树是+子树,右子树是/子树(根为/,左e、右f)
步骤 2:从最底层子树开始中序遍历
中序遍历规则是:左子树 → 根节点 → 右子树。
子树 1:以-(根,子节点c、d)
- 中序遍历左子树
c→ 访问根-→ 中序遍历右子树d - 遍历结果:
c - d
子树 2:以*(根,子节点b、[c-d])
- 中序遍历左子树
b→ 访问根*→ 中序遍历右子树[c-d] - 遍历结果:
b * c - d
子树 3:以+(根,子节点a、[b*c-d])
- 中序遍历左子树
a→ 访问根+→ 中序遍历右子树[b*c-d] - 遍历结果:
a + b * c - d
子树 4:以/(根,子节点e、f)
- 中序遍历左子树
e→ 访问根/→ 中序遍历右子树f - 遍历结果:
e / f
步骤 3:遍历整棵树(根为-,子节点[a+b*c-d]、[e/f])
整棵树的根是最顶层的-,按照 "左子树 → 根 → 右子树" 规则:
- 中序遍历左子树
[a + b * c - d]→ 访问根-→ 中序遍历右子树[e / f]
最终拼接结果:a + b * c - d - e / f
为什么 "d 之后会输出根节点 -"?
因为d是左子树(+子树)的最后一个节点 ,遍历完左子树后,就会回到整棵树的根节点-,所以d之后会输出这个根节点-,再继续遍历右子树e/f。
三种遍历的叶子节点的先后顺序

完全相同。
二叉树的遍历顺序(先序:根→左→右;中序:左→根→右;后序:左→右→根),叶子节点没有子节点 ,因此对叶子节点的遍历逻辑是:
无论先序、中序、后序,叶子节点的访问顺序都遵循 "从左到右" 的自然顺序(因为叶子节点的 "左 / 右子树" 为空,遍历顺序只由它在树中的左右位置决定)。
例如:一棵简单的二叉树(根为A,左叶子B,右叶子C)
- 先序序列:
A → B → C(叶子顺序B→C) - 中序序列:
B → A → C(叶子顺序B→C) - 后序序列:
B → C → A(叶子顺序B→C)
可见所有叶子节点的先后顺序完全一致。
2 线索二叉树
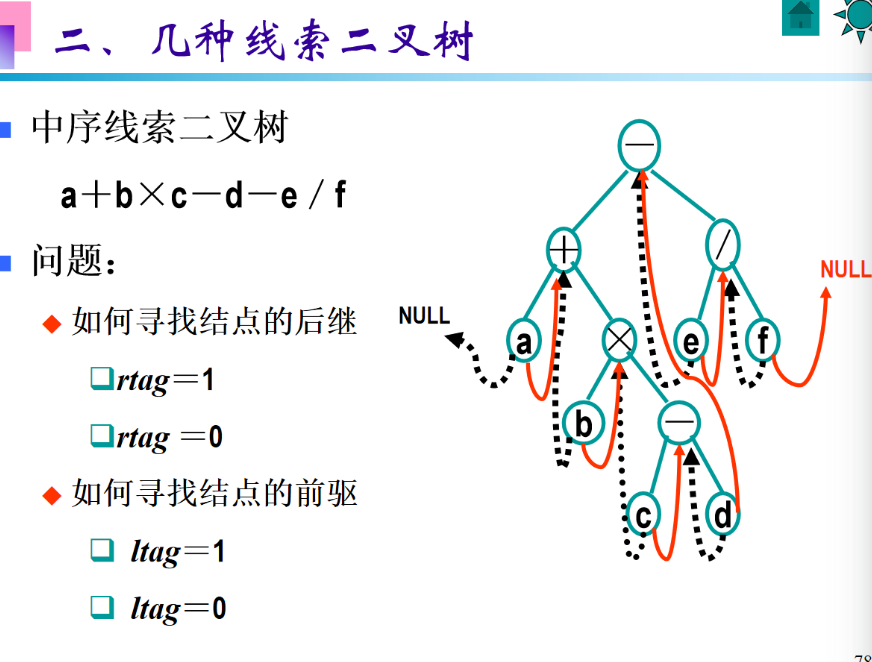
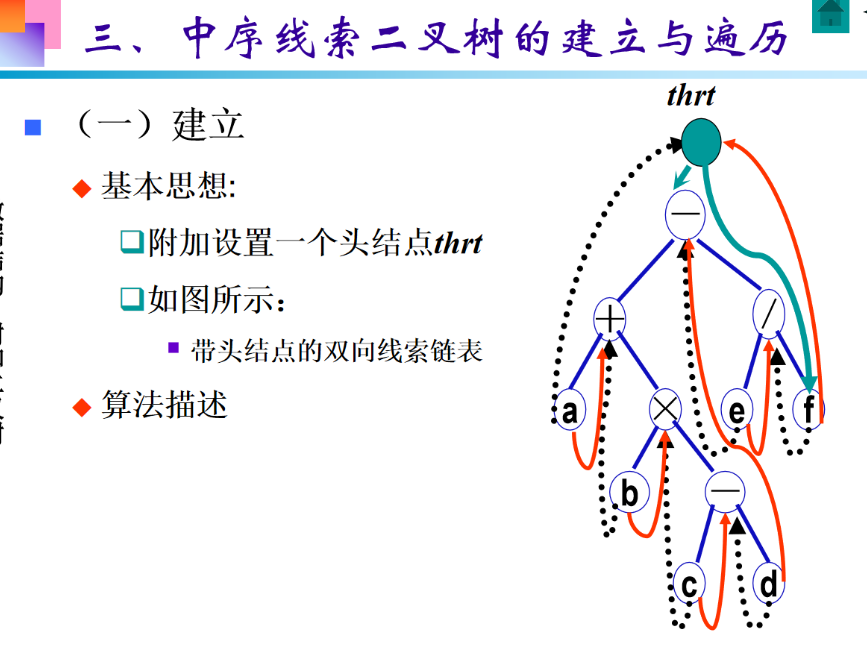
中序线索二叉树的线索连接原则 是:用 "线索" 替代二叉树中原本为空的左、右指针,指向该节点在中序遍历序列中的前驱 / 后继节点(中序遍历的顺序是 "左→根→右")。
具体连接规则(结合你提供的图):
- 空左指针→线索 :节点的左指针若为空,改为指向该节点在中序遍历中的前驱节点 (图中用黑色虚线表示);
- 空右指针→线索 :节点的右指针若为空,改为指向该节点在中序遍历中的后继节点 (图中用红色实线表示);
- 头结点 thrt 的特殊连接:头结点的左指针指向二叉树的根节点,右指针指向中序遍历的最后一个节点;同时,中序遍历的第一个节点的左指针、最后一个节点的右指针都指向头结点,形成双向循环链表。
以图中的节点为例(中序遍历序列是a + b * c - d - e / f):
- 节点
a(中序第一个节点):左指针为空,线索指向头结点thrt;右指针为空,线索指向其后继节点+; - 节点
f(中序最后一个节点):左指针为空,线索指向其前驱节点/;右指针为空,线索指向头结点thrt; - 节点
c:右指针为空,线索指向其后继节点-(中间的-)。
简单说:线索是 "中序遍历顺序的前后关系" 在二叉树中的指针化体现,空指针不再闲置,而是记录遍历的前驱 / 后继。
3 树的二叉链表存储
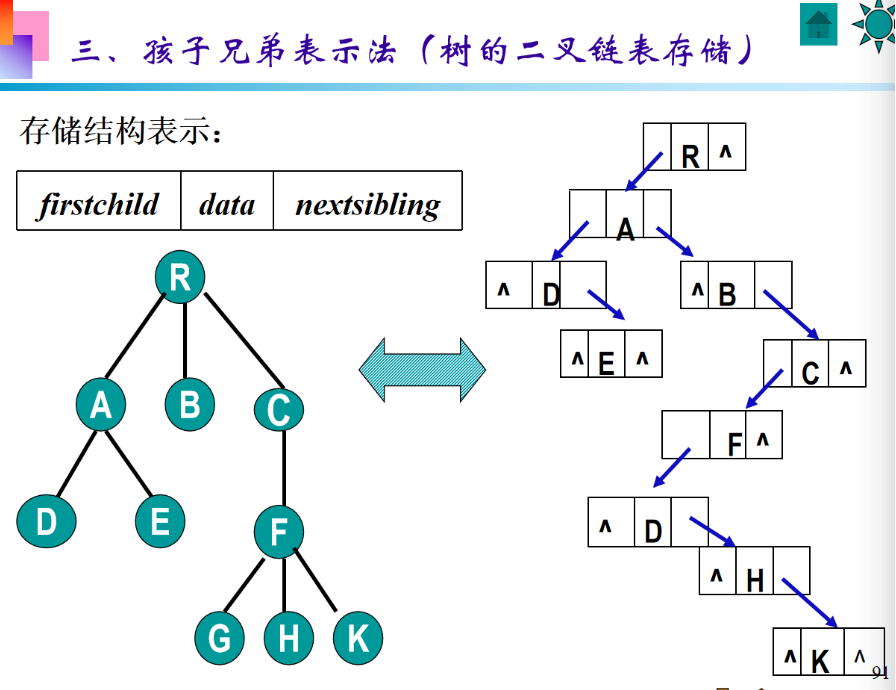
(注意后面这个D写错了,倒数第3个里面应该写的是G)
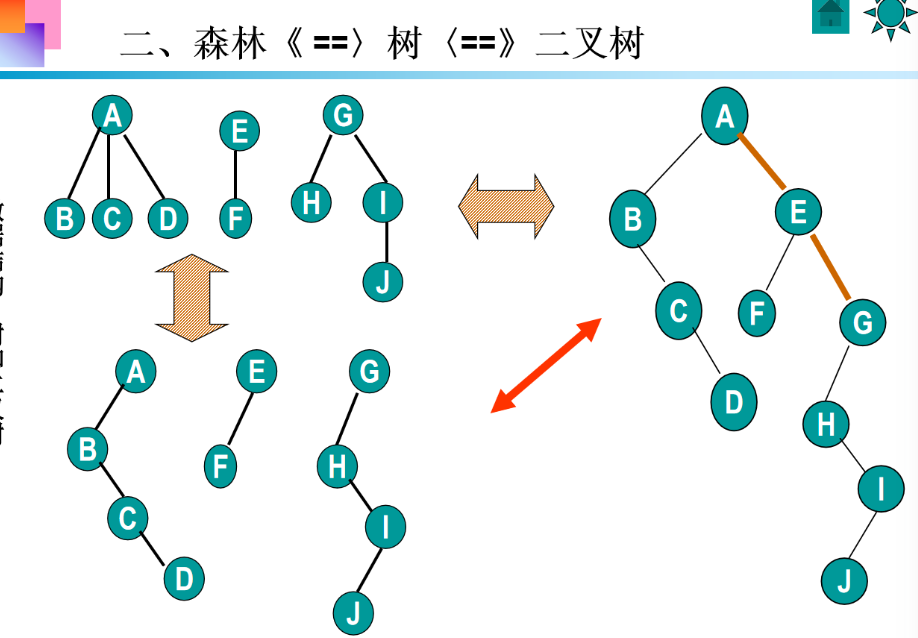
4 树、森林、二叉树的转换


步骤 1:加线 ------ 兄弟相连
- 操作:在普通树中,同一个父节点的所有子节点(即兄弟节点)之间,从左到右依次用线连接起来。
- 作用:标记兄弟节点的顺序关系,为后续转换为二叉树的 "右兄弟" 指针做准备。
步骤 2:抹线 ------ 长兄为父
- 操作:保留父节点与 ** 第一个子节点(长兄)** 的连线,删除父节点与其他子节点的连线。
- 作用:将普通树的 "父 - 多子" 关系,简化为二叉树的 "父 - 左孩子" 关系(长兄作为父节点的左孩子)。
步骤 3:旋转 ------ 孩子靠左
- 操作 :将整个结构以父节点为中心,顺时针旋转一定角度,使每个节点的左子节点是原树的子节点,右子节点是原树的兄弟节点。
- 作用:最终形成二叉树的 "左孩子右兄弟" 结构(符合二叉树的节点最多有 2 个子节点的规则)。
5 层次遍历二叉树
二叉树的递归/层序遍历 | labuladong 的算法笔记


cpp最简单的写法,回头来看也不过BFS遍历,c用队列模拟。
cpp
void levelOrderTraverse(TreeNode* root) {
if (root == nullptr) {
return;
}
std::queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode* cur = q.front();
q.pop();
// 访问 cur 节点
std::cout << cur->val << std::endl;
// 把 cur 的左右子节点加入队列
if (cur->left != nullptr) {
q.push(cur->left);
}
if (cur->right != nullptr) {
q.push(cur->right);
}
}
}6 习题
二叉树的度

答案是 B 。
二叉树的 "度" 是指树中所有节点的度的最大值(节点的度是该节点的子节点数量)。
由于二叉树的每个节点最多有 2 个子节点,因此二叉树的度最大为 2,但可以小于 2。
完全二叉树的顺序存储规则

这道题考查的是完全二叉树的顺序存储规则 ,但题目中的二叉树并没有说明是 "完全二叉树",因此答案是 D(无法确定),原因如下:
核心知识点:完全二叉树的顺序存储规则
只有完全二叉树(节点按 "从上到下、从左到右" 填满的二叉树),才能用 "第i个节点的左孩子是2i,右孩子是(2i+1)" 的规则确定位置(这也是选项 A、B 的依据)。
题目中的二叉树不满足 "完全二叉树" 条件
题目只说 "按层次存储在数组中",但普通二叉树(非完全二叉树)按层次存储时,节点的位置与 "2i、(2i+1)" 的规则无关。
例如:一棵普通二叉树(根节点 1,右孩子 2,无左孩子),按层次存储到数组中是[1,2]。此时根节点 1 的右孩子是 2,但按 "(2i+1)" 计算应为 3(超出数组范围),与实际位置不符。
因此,只有完全二叉树才能用 "2i、(2i+1)" 确定孩子位置,而题目中的二叉树未说明是完全二叉树,所以无法确定右孩子的位置。
二叉树的节点数与高度(深度)的关系

核心逻辑:
仅含度 0(叶子)和度 2 节点的二叉树,
"最少节点数" 的结构是 "满二叉树的单支扩展"
高度(h=4) 的示例:
cpp
第1层: 1(度2)
/ \
第2层: 2(度2) 3(度0)
/ \
第3层: 4(度2) 5(度0)
/ \
第4层: 6 7(均为度0)要让节点数最少,需保证每一层尽可能少节点,同时满足 "只有度 0 和度 2 节点" 的条件:
- 高度为h的二叉树,第 1 层(根)有 1 个节点(度 2);
- 第 2 层:根的 2 个孩子(度 2),共 2 个节点;
- 第 3 层到第 h-1 层:每个节点都是度 2,每层节点数与上层相同;
- 第h层:所有节点都是度 0(叶子),共 2 个节点。
公式推导
这种 "最少节点" 的二叉树,结构等价于深度为h的满二叉树的最小形态,
节点数公式为:{最少节点数} = 2h - 1
例如:
h=1时,节点数 1(2×1-1=1);
h=2时,节点数 3(2×2-1=3);
h=3时,节点数 5(2×3-1=5),均符合 "仅度 0 和度 2 节点" 的条件)
因此答案是(2h-1)(选项 B)。
二叉树的顺序存储(完全二叉树形式)
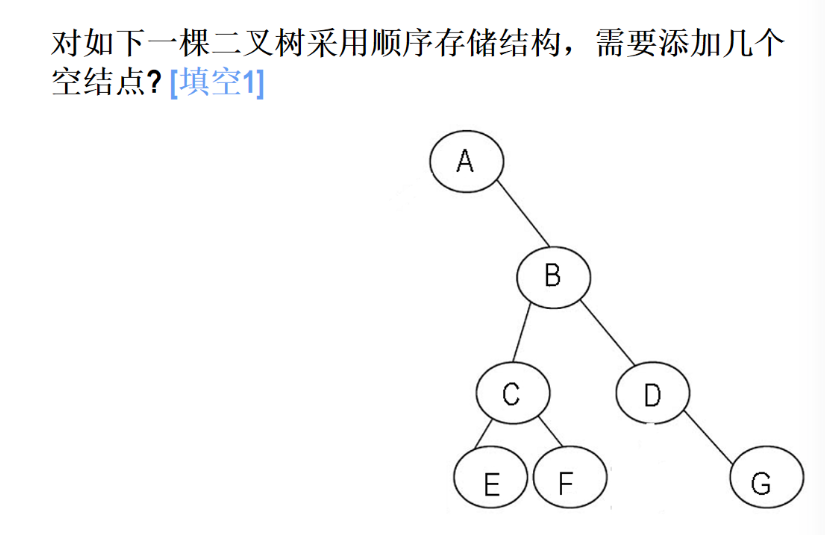
核心思路是:顺序存储需将二叉树补为 "完全二叉树",统计补全后总节点数与原节点数的差值,即为需要添加的空节点数。
