基于 MATLAB 的 AM/DSB-SC/VSB 模拟调制与解调仿真及性能对比研究

杰瑞不懂代码2025-12-28 12:37

文章目录

一、前言

模拟调制作为经典模拟通信系统的核心内容，既是频谱搬移思想最直观的载体，也是理解"带宽占用---解调复杂度---抗噪性能"三者权衡关系的基础。在通信实验中，AM（带载波幅度调制） 、DSB-SC（抑制载波双边带） 以及 VSB（残留边带） 通常被用作三个层次的代表：AM 强调包络可检波与实现简洁性，DSB-SC 强调同步解调与载波恢复的重要性，而 VSB 则体现频谱效率与系统工程折中的设计思想。

本文给出一个基于 MATLAB 的端到端仿真程序，用于对上述三类调制方式完成同一基带信号条件下的调制、信道扰动（AWGN）与解调恢复，并通过均方误差（MSE）、输出信噪比（SNR_out）以及带宽与功率效率等指标进行定量对比。

二、程序整体功能概述

本程序实现了一个较完整的模拟调制仿真链路，其核心思想是在统一的采样框架下构造多类基带信号，分别进行 AM、DSB-SC 与 VSB 调制，再引入加性高斯白噪声信道模型，并在接收端采用包络检波或相干解调完成恢复，最终以可视化与统计指标给出结论。为避免对单一测试信号的结论偏置，程序设计了三类基带源：单音正弦用于验证理论谱线与调制规律，多音叠加用于模拟语音/音乐中"离散谱成分"的典型结构，带限随机过程作为类语音信号用于观察连续谱条件下的带宽占用与噪声敏感性差异。

在调制部分，AM 采用带载波形式，其数学模型可写为
s A M ( t ) = ( 1 + μ m ( t ) ) cos ⁡ ( 2 π f c t ) s_{\mathrm{AM}}(t) = \bigl(1+\mu m(t)\bigr)\cos(2\pi f_c t) sAM(t)=(1+μm(t))cos(2πfct)其中 m ( t ) m(t) m(t) 为归一化后的基带信号， μ \mu μ 为调制指数。该形式既可用于演示欠调制/正常调制/过调制时包络形态的变化，也便于后续以包络检波与相干解调两种方式进行对比。DSB-SC 采用抑制载波的双边带形式
s D S B ( t ) = m ( t ) cos ⁡ ( 2 π f c t ) s_{\mathrm{DSB}}(t)=m(t)\cos(2\pi f_c t) sDSB(t)=m(t)cos(2πfct)其频域表现为载波分量显著降低，能量集中于两侧边带。VSB 在 DSB-SC 基础上引入残留边带滤波器，通过保留一侧边带并对另一侧边带进行部分保留与平滑过渡，实现带宽占用的降低，同时仍保持可行的相干解调路径。

信道部分采用 AWGN 模型，以输入 SNR（20/10/0 dB）三组条件对比性能趋势。解调部分中，AM 同时给出基于 Hilbert 变换的包络提取与基于乘法器+低通的相干解调；DSB-SC 与 VSB 采用相干解调，并进一步对 DSB-SC 引入本振相位偏差（0°/20°/60°）用于刻画同步误差的影响。

性能评估层面，程序对恢复信号与原信号计算 MSE，并给出输出 SNR 的估计，同时统计理论带宽占用与功率效率，从"频谱效率---实现复杂度---抗噪表现"三个维度完成综合比较。

三、系统模型与关键实现思路

3.1 统一采样框架与参数设计依据

为保证时域仿真与频域分析的精度一致性，程序采用统一采样率 F s F_s Fs 与固定时长 T T T 构造离散时间序列 t = n / F s t=n/F_s t=n/Fs。参数选择遵循两条基本原则 ：其一，为降低载波调制下离散化误差并使频谱峰值更清晰，采样率设置为远大于载波频率的数量级（满足 F s > 10 f c F_s>10f_c Fs>10fc 的经验条件）；其二，为使 FFT 分辨率能够细致区分基带频率成分与边带结构，仿真时长设置为包含足够多的基带周期，从而使频域谱线更接近理想离散峰值或连续谱包络。

在本文配置中， F s = 400 kHz F_s=400\ \text{kHz} Fs=400 kHz、 f c = 20 kHz f_c=20\ \text{kHz} fc=20 kHz、基带最高频率 f m , max ⁡ = 1 kHz f_{m,\max}=1\ \text{kHz} fm,max=1 kHz、仿真时长 T = 50 ms T=50\ \text{ms} T=50 ms，由此采样点数 N = F s T = 2 × 10 4 N=F_sT=2\times 10^4 N=FsT=2×104。该配置在不显著增加计算量的前提下，为时域波形细节、频谱边带位置标注以及噪声背景的可视化提供了稳定的数值基础。

3.2 基带信号构造与归一化处理

基带部分采用"可解释的三类信号源"以覆盖典型情况：单音正弦用于验证频谱对称性与调制搬移；多音叠加用于模拟多个离散谱线同时存在时的边带结构；带限随机过程用于近似类语音信号的连续谱形态。为了使不同信号在调制指数与噪声强度对比中具有可比性，所有基带信号统一进行幅度归一化，使其幅度落入 [ − 1 , 1 ] [-1,1] [−1,1] 区间，从而在 AM 中 1 + μ m ( t ) 1+\mu m(t) 1+μm(t) 的"包络非负条件"能够直接由 μ \mu μ 控制，避免信号幅度差异导致的额外偏置。

对类语音信号，程序先生成零均值白噪声，再通过低通滤波限制其带宽至 f m , max ⁡ f_{m,\max} fm,max，以获得在频域上连续且带限的基带谱形。该处理能较好体现模拟语音信号的能量集中区间，并使后续对带宽占用、残留边带与噪声敏感性的讨论更具代表性。

3.3 三类调制与解调链路的实现要点

AM 调制采用带载波结构，其核心在于调制指数 μ \mu μ 的选择直接决定包络是否发生交越。理论上，当 μ ≤ 1 \mu\le 1 μ≤1 且 m ( t ) ∈ [ − 1 , 1 ] m(t)\in[-1,1] m(t)∈[−1,1] 时，包络保持非负，包络检波能够在理想条件下恢复基带；当 μ > 1 \mu>1 μ>1 时，包络出现"翻转区间"，包络检波将产生明显失真，而相干解调在本振同步条件下仍可实现线性恢复。因此程序以 μ = 0.3 / 0.8 / 1.2 \mu=0.3/0.8/1.2 μ=0.3/0.8/1.2 三种典型状态进行对比，一方面展示包络几何意义，另一方面通过 MSE 量化不同解调方式的误差特征。

DSB-SC 调制的关键在于载波抑制后的同步需求。相干解调通常采用乘法器将信号与本振相乘，再通过低通滤波提取基带分量。若本振存在相位偏差 ϕ \phi ϕ，恢复信号幅度将按 cos ⁡ ϕ \cos\phi cosϕ 衰减，且在较大偏差下表现为显著失真。基于此，程序设置 ϕ = 0 ∘ / 20 ∘ / 60 ∘ \phi=0^\circ/20^\circ/60^\circ ϕ=0∘/20∘/60∘ 以观察从轻微同步误差到严重失配的性能变化，并用 MSE 给出定量结果。

VSB 调制部分的核心在于滤波器频响的构造。程序采用频域法直接设计残留边带滤波器 H V S B ( f ) H_{\mathrm{VSB}}(f) HVSB(f)，在载波附近引入具有平滑过渡特性的滚降区，使一侧边带基本保留，另一侧边带仅残留必要部分，从而在降低带宽占用的同时尽量减小解调幅度失真。该实现的优势在于参数可控、可视化直观，能够直接在频域比较 DSB-SC 与 VSB 的谱形差异。接收端同样采用相干解调并低通滤波恢复基带，随后通过误差曲线与 MSE 评估残留边带引入的幅度/相位畸变。

3.4 AWGN 条件下的性能评估与对比指标

为在统一基带与载波条件下比较抗噪性能，程序在调制信号上叠加加性高斯白噪声，并对三组输入 SNR 进行对比。评价指标以恢复误差的均方值为主：
M S E = 1 L ∑ n = 1 L ( m [ n ] − m ^ [ n ] ) 2 \mathrm{MSE}=\frac{1}{L}\sum_{n=1}^{L}\bigl(m[n]-\hat m[n]\bigr)^2 MSE=L1n=1∑L(m[n]−m^[n])2并结合输出 SNR 的估计作为补充，从而形成"误差大小---主观波形一致性---频谱噪声底抬升"三位一体的判断依据。此外，程序给出理论带宽占用的估计：AM 与 DSB-SC 的理论带宽近似为 2 f m , max ⁡ 2f_{m,\max} 2fm,max，VSB 在残留边带宽度 α \alpha α 下可近似为 f m , max ⁡ + α f_{m,\max}+\alpha fm,max+α，并据此完成带宽效率层面的定量对比。功率效率方面，AM（带载波）存在较多功率消耗在载波分量上，DSB-SC 与 VSB 则更倾向于将功率集中于信息承载的边带分量，该差异在综合对比图中给出直观呈现。

四、关键代码片段

一、信号生成

matlab 复制代码 
% 信号1：单音正弦信号
m1 = cos(2*pi*fm1*t);
m1 = m1 / max(abs(m1));  % 归一化到[-1,1]

% 信号2：多音信号 (300+600+900 Hz)
m2 = cos(2*pi*f_multi(1)*t) + 0.8*cos(2*pi*f_multi(2)*t) + 0.6*cos(2*pi*f_multi(3)*t);
m2 = m2 / max(abs(m2));  % 归一化到[-1,1]

% 信号3：类语音信号 (带限随机过程)
rng(42);  % 固定随机种子，保证可重复性
white_noise = randn(1, N);
% 设计低通滤波器，截止频率为fm_max
[b_lp, a_lp] = butter(6, fm_max/(Fs/2));
m3 = filter(b_lp, a_lp, white_noise);
m3 = m3 / max(abs(m3));  % 归一化到[-1,1]

二、AM调制与解调

matlab 复制代码 
% 使用多音信号进行AM调制演示
m_am = m2;  % 选择多音信号

% 载波信号
carrier = cos(2*pi*fc*t);

% 不同调制指数的AM调制
figure('Name', 'AM调制 - 不同调制指数对比', 'Position', [100, 100, 1400, 800]);
tiledlayout(3, 3, 'TileSpacing', 'compact', 'Padding', 'compact');

s_am = cell(1, 3);
for i = 1:length(mu_values)
    mu = mu_values(i);
    % AM调制: s_AM(t) = (1 + μ*m(t)) * cos(2πfct)
    s_am{i} = (1 + mu * m_am) .* carrier;
    
    % 时域波形
    nexttile;
    plot(t*1000, s_am{i}, 'b', 'LineWidth', 0.5);
    hold on;
    plot(t*1000, 1 + mu*m_am, 'r--', 'LineWidth', 1);  % 上包络
    plot(t*1000, -(1 + mu*m_am), 'r--', 'LineWidth', 1);  % 下包络
    xlabel('时间 (ms)'); ylabel('幅度');
    if mu < 1
        title(sprintf('AM调制 \\mu=%.1f (欠调制)', mu));
    elseif mu == 1
        title(sprintf('AM调制 \\mu=%.1f (临界调制)', mu));
    else
        title(sprintf('AM调制 \\mu=%.1f (过调制)', mu));
    end
    xlim([0, 5]); grid on;
    legend('调制信号', '包络', 'Location', 'best');
end

% 频谱对比
for i = 1:length(mu_values)
    mu = mu_values(i);
    nexttile;
    [S_AM, f_am] = calc_spectrum(s_am{i}, Fs, N);
    plot(f_am/1000, abs(S_AM), 'b', 'LineWidth', 1);
    xlabel('频率 (kHz)'); ylabel('幅度');
    title(sprintf('AM频谱 \\mu=%.1f', mu));
    xlim([fc/1000-3, fc/1000+3]); grid on;
    xline(fc/1000, 'r--', 'f_c', 'LineWidth', 1.5);
    xline((fc-fm_max)/1000, 'g--', 'LSB', 'LineWidth', 1);
    xline((fc+fm_max)/1000, 'g--', 'USB', 'LineWidth', 1);
end

% 局部放大 - 过调制失真
for i = 1:length(mu_values)
    mu = mu_values(i);
    nexttile;
    plot(t*1000, s_am{i}, 'b', 'LineWidth', 1);
    hold on;
    plot(t*1000, 1 + mu*m_am, 'r-', 'LineWidth', 1.5);
    xlabel('时间 (ms)'); ylabel('幅度');
    title(sprintf('局部放大 \\mu=%.1f', mu));
    xlim([10, 15]); grid on;
    if mu > 1
        % 标注过调制区域
        idx_over = find((1 + mu*m_am) < 0);
        if ~isempty(idx_over)
            plot(t(idx_over)*1000, zeros(size(idx_over)), 'mo', 'MarkerSize', 3);
        end
    end
end

三、DSB-SC调制与解调区

matlab 复制代码 
phase_offsets = [0, 20, 60];  % 相位偏差 (度)
mse_dsb_phase = zeros(1, 3);

for i = 1:length(phase_offsets)
    phi = phase_offsets(i) * pi / 180;  % 转换为弧度
    
    % 带相位偏差的本振
    carrier_offset = cos(2*pi*fc*t + phi);
    
    % 相干解调
    s_demod = s_dsb .* carrier_offset * 2;
    m_dsb_rec = lowpass_fir(s_demod, fm_max*1.5, Fs, 100);
    
    % 计算MSE
    valid_range = 1000:N-1000;
    mse_dsb_phase(i) = mean((m_dsb(valid_range) - m_dsb_rec(valid_range)).^2);
    
    nexttile;
    plot(t*1000, m_dsb, 'b', 'LineWidth', 1); hold on;
    plot(t*1000, m_dsb_rec, 'r--', 'LineWidth', 1);
    xlabel('时间 (ms)'); ylabel('幅度');
    title(sprintf('相干解调 \\phi=%d°, MSE=%.4f', phase_offsets(i), mse_dsb_phase(i)));
    xlim([10, 30]); grid on;
    legend('原始', '恢复', 'Location', 'best');
    
    % 理论幅度衰减
    theoretical_attn = cos(phi);
    fprintf('    phi=%d°: 理论衰减=%.3f, MSE=%.6f\n', phase_offsets(i), theoretical_attn, mse_dsb_phase(i));
end

四、DSB-SC vs AM 噪声性能对比

matlab 复制代码 
for i = 1:length(SNR_values)
    snr = SNR_values(i);
    
    % 添加AWGN噪声
    s_am_noisy = add_awgn(s_am_08, snr);
    s_dsb_noisy = add_awgn(s_dsb, snr);
    
    % AM包络检波
    env_am = abs(hilbert(s_am_noisy));
    m_am_rec = env_am - mean(env_am);
    m_am_rec = m_am_rec / max(abs(m_am_rec)) * max(abs(m_am));
    
    % DSB-SC相干解调
    s_demod_dsb = s_dsb_noisy .* carrier * 2;
    m_dsb_rec = lowpass_fir(s_demod_dsb, fm_max*1.5, Fs, 100);
    
    % 计算MSE和输出SNR
    valid_range = 1000:N-1000;
    mse_am_noise(i) = mean((m_am(valid_range) - m_am_rec(valid_range)).^2);
    mse_dsb_noise(i) = mean((m_dsb(valid_range) - m_dsb_rec(valid_range)).^2);
    
    e_am = m_am(valid_range) - m_am_rec(valid_range);
    e_dsb = m_dsb(valid_range) - m_dsb_rec(valid_range);
    snr_out_am(i) = 10*log10(mean(m_am(valid_range).^2)/mean(e_am.^2));
    snr_out_dsb(i) = 10*log10(mean(m_dsb(valid_range).^2)/mean(e_dsb.^2));
    
    % AM恢复结果
    nexttile;
    plot(t*1000, m_am, 'b', 'LineWidth', 1); hold on;
    plot(t*1000, m_am_rec, 'r--', 'LineWidth', 0.8);
    xlabel('时间 (ms)'); ylabel('幅度');
    title(sprintf('AM恢复 SNR=%ddB', snr));
    xlim([15, 35]); grid on;
    
    % DSB-SC恢复结果
    nexttile;
    plot(t*1000, m_dsb, 'b', 'LineWidth', 1); hold on;
    plot(t*1000, m_dsb_rec, 'g--', 'LineWidth', 0.8);
    xlabel('时间 (ms)'); ylabel('幅度');
    title(sprintf('DSB-SC恢复 SNR=%ddB', snr));
    xlim([15, 35]); grid on;
    
    % 噪声信号频谱
    nexttile;
    [S_AM_N, f_n] = calc_spectrum(s_am_noisy, Fs, N);
    plot(f_n/1000, 20*log10(abs(S_AM_N)+eps), 'b', 'LineWidth', 0.5);
    xlabel('频率 (kHz)'); ylabel('幅度 (dB)');
    title(sprintf('AM噪声频谱 SNR=%ddB', snr));
    xlim([fc/1000-5, fc/1000+5]); ylim([-80, 0]); grid on;
    
    % 误差对比
    nexttile;
    plot(t*1000, m_am - m_am_rec, 'r', 'LineWidth', 0.5); hold on;
    plot(t*1000, m_dsb - m_dsb_rec, 'g', 'LineWidth', 0.5);
    xlabel('时间 (ms)'); ylabel('误差');
    title(sprintf('解调误差 SNR=%ddB', snr));
    xlim([15, 35]); grid on;
    legend('AM', 'DSB-SC', 'Location', 'best');
end

五、VSB调制与解调

matlab 复制代码 
% 使用多音信号进行VSB调制
m_vsb = m2;

% 首先生成DSB-SC信号
s_dsb_vsb = m_vsb .* carrier;

% 设计VSB滤波器 (频域法)
% VSB滤波器: 保留上边带 + 下边带残留部分
% 使用raised-cosine过渡特性

% 频率向量
f_vec = (-N/2:N/2-1) * (Fs/N);

% VSB滤波器频率响应设计
% 中心频率为fc，保留上边带，下边带用raised-cosine过渡
H_vsb = zeros(1, N);
alpha = vsb_rolloff;  % 过渡带宽度

for k = 1:N
    f = f_vec(k);
    
    % 正频率部分
    if f >= 0
        if f >= fc + alpha && f <= fc + fm_max + alpha
            % 上边带完全通过
            H_vsb(k) = 1;
        elseif f >= fc - alpha && f < fc + alpha
            % 过渡带 (raised-cosine)
            H_vsb(k) = 0.5 * (1 + cos(pi * (f - fc) / (2*alpha)));
        elseif f >= fc + fm_max + alpha
            % 超出上边带
            H_vsb(k) = 0;
        elseif f < fc - alpha
            % 下边带被抑制
            H_vsb(k) = 0;
        end
    else
        % 负频率部分 (对称)
        f_pos = -f;
        if f_pos >= fc + alpha && f_pos <= fc + fm_max + alpha
            H_vsb(k) = 1;
        elseif f_pos >= fc - alpha && f_pos < fc + alpha
            H_vsb(k) = 0.5 * (1 + cos(pi * (f_pos - fc) / (2*alpha)));
        else
            H_vsb(k) = 0;
        end
    end
end

% 应用VSB滤波器 (频域)
S_DSB_VSB = fftshift(fft(s_dsb_vsb));
S_VSB = S_DSB_VSB .* H_vsb;
s_vsb = real(ifft(ifftshift(S_VSB)));

五、仿真结果展示

基带信号分析

AM调制情况下不同调制指数对比图

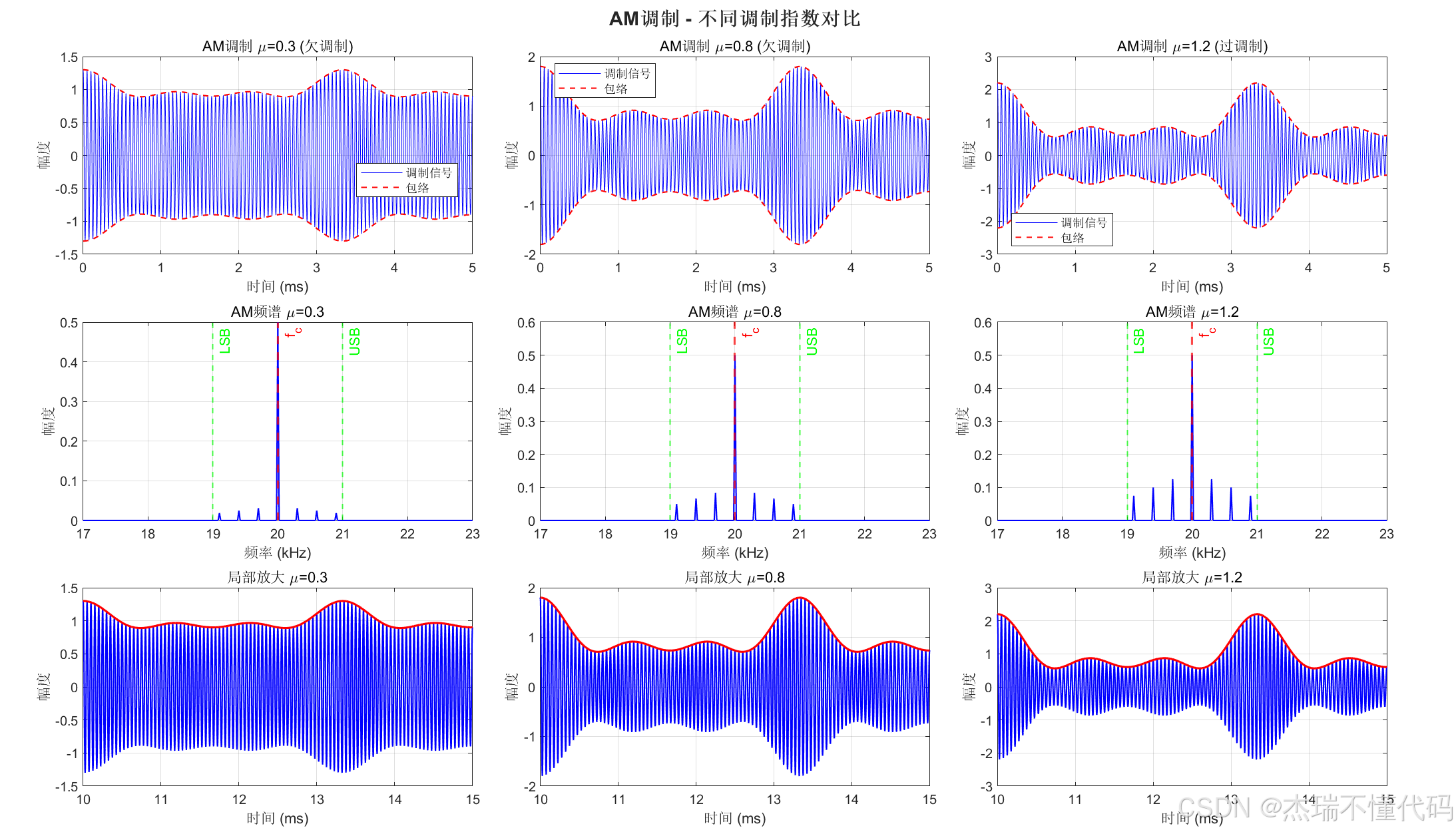
AM解调方式对比

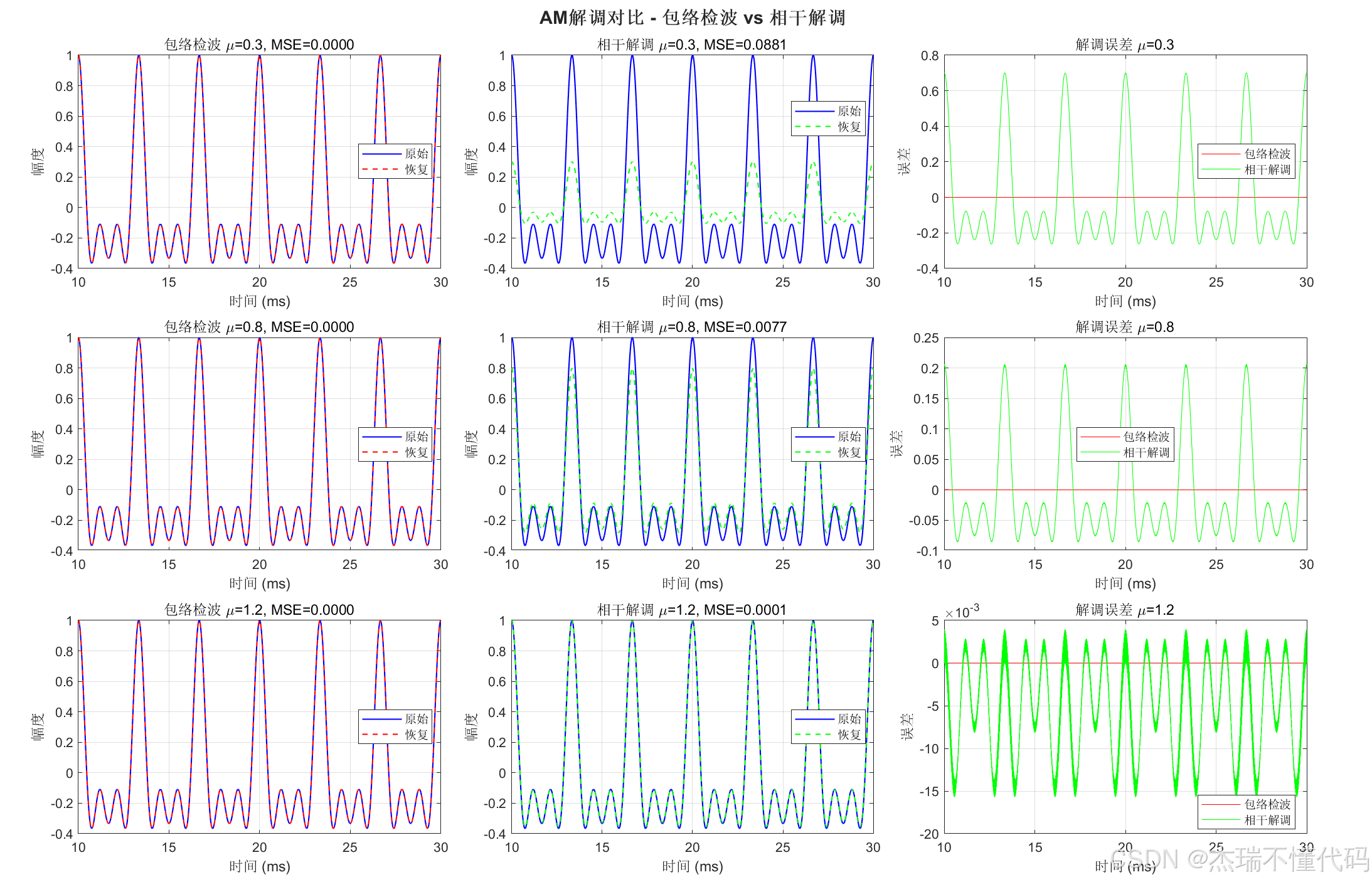
DSB-SC调制解调分析

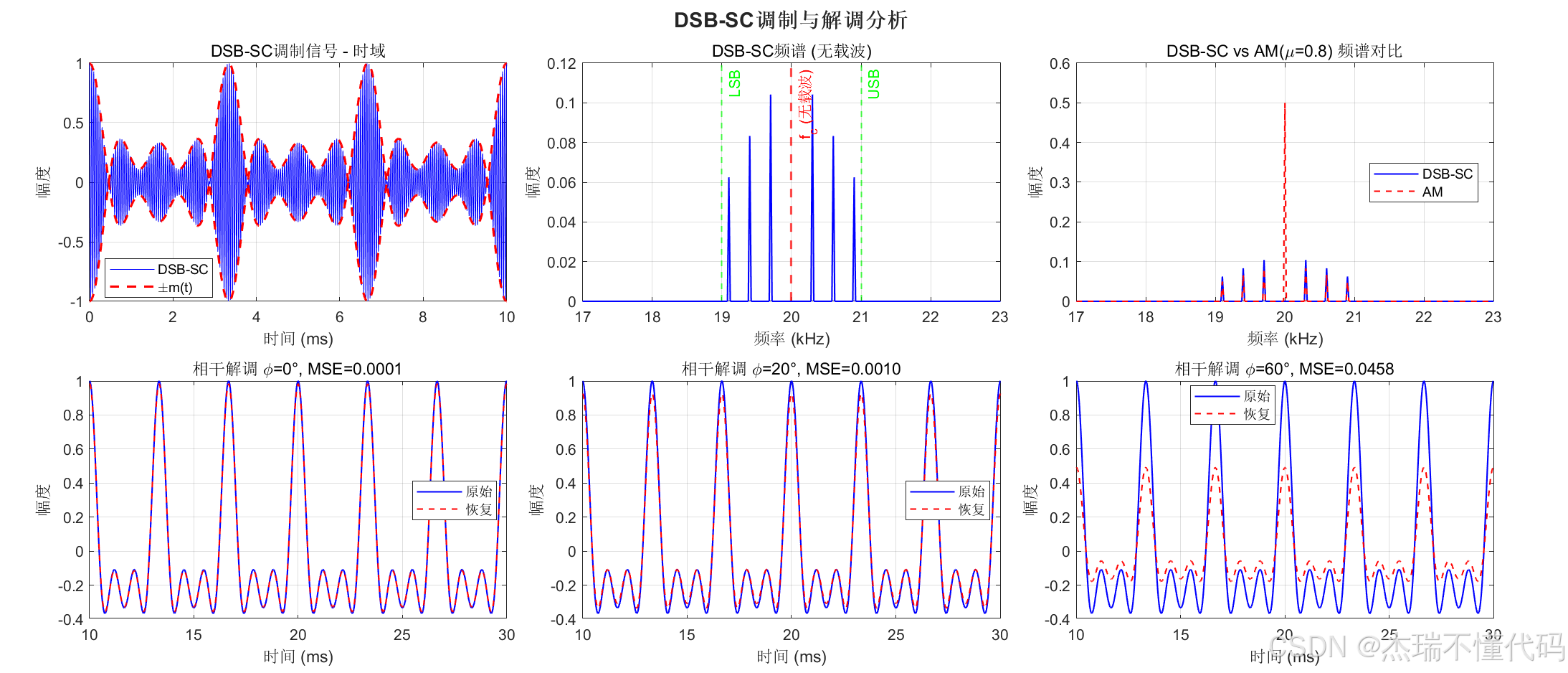
AM和DSB-SC噪声性能对比图

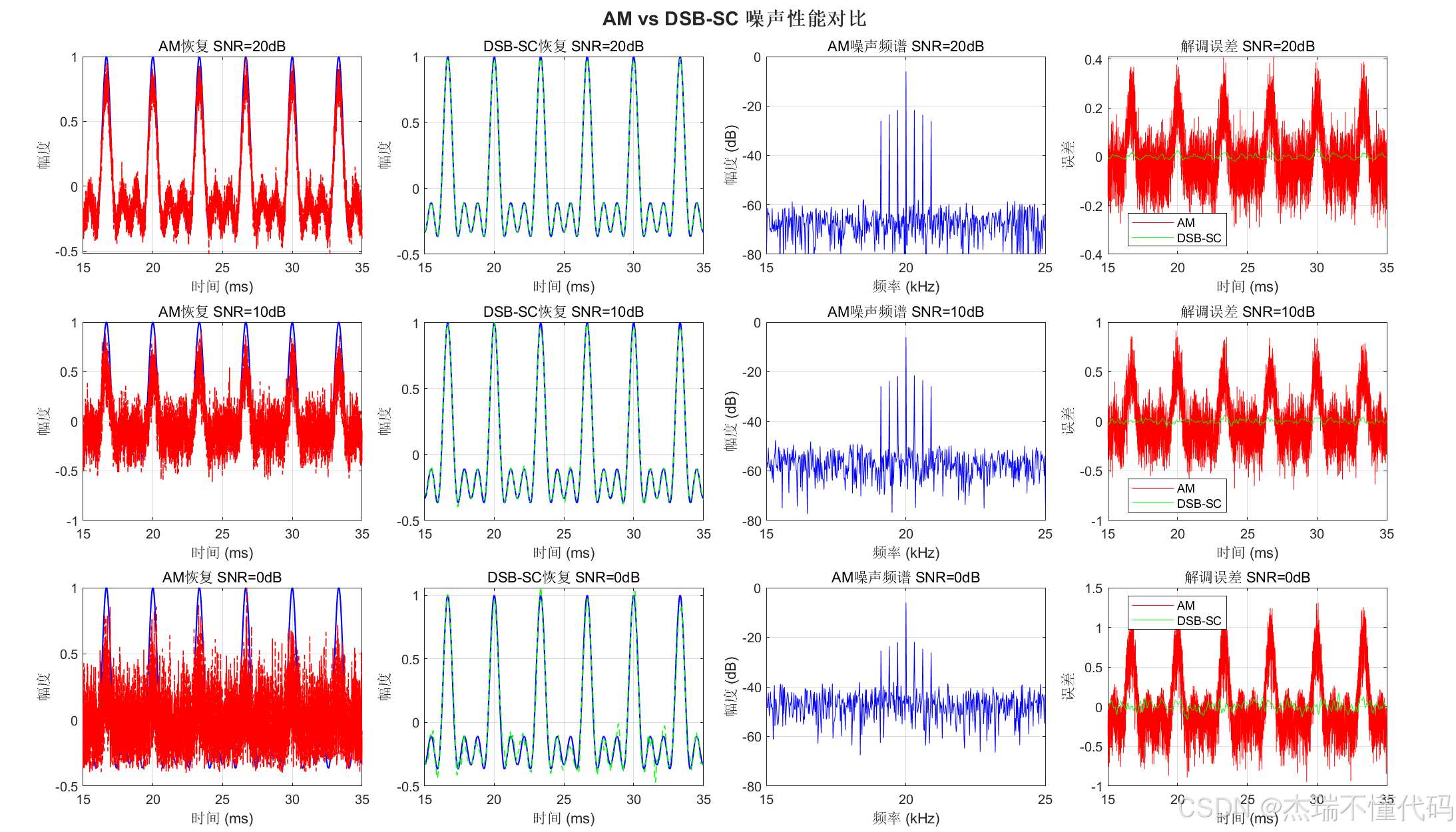
图太多啦，看一个总览吧~

由于源代码很长，无法直接全部粘在这，因此挑了一些关键的部分予以展示，如果你对完整源码、可运行工程文件或拓展版本 感兴趣，欢迎留言交流，后续也会继续分享更多通信系统仿真相关内容，我是不懂代码的杰瑞学长，我们下期再见！

如果觉得文章对你有帮助，欢迎点赞 + 收藏 + 关注，一起进步！

相关推荐
沐知全栈开发4 小时前
Perl 数据库连接
开发语言
森叶5 小时前
Java 比 Python 高性能的原因：重点在高并发方面
java·开发语言·python
qq_316837755 小时前
uni.chooseMedia 读取base64 或 二进制
开发语言·前端·javascript
方圆工作室5 小时前
【C语言图形学】用*号绘制完美圆的三种算法详解与实现【AI】
c语言·开发语言·算法
小二·6 小时前
Python Web 开发进阶实战：混沌工程初探 —— 主动注入故障，构建高韧性系统
开发语言·前端·python
Lkygo6 小时前
LlamaIndex使用指南
linux·开发语言·python·llama
进阶小白猿6 小时前
Java技术八股学习Day20
java·开发语言·学习
代码村新手6 小时前
C++-类和对象(中)
java·开发语言·c++
葵花楹6 小时前
【JAVA课设】【游戏社交系统】
java·开发语言·游戏
赵谨言6 小时前
Python串口的三相交流电机控制系统研究
大数据·开发语言·经验分享·python
热门推荐
01GitHub 镜像站点022025 Telegram 最新免费社工库机器人（LetsTG可[特殊字符]）搭建指南（含 Python 脚本）032025年大语言模型技术全景报告04Linux下V2Ray安装配置指南05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06UV安装并设置国内源07Labelme从安装到标注：零基础完整指南08Claude Code Skills 实用使用手册09AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南10BongoCat - 跨平台键盘猫动画工具