文章目录
- [一 基础知识:四种攻击类型(重点)](#一 基础知识:四种攻击类型(重点))
- [二 模块化构造知识体系图(重点)](#二 模块化构造知识体系图(重点))
- [三 公钥加密方案定义](#三 公钥加密方案定义)
- [四 公钥加密的CPA不可区分实验(重点)](#四 公钥加密的CPA不可区分实验(重点))
- [五 完美安全的公钥加密方案的不可能性(重点)](#五 完美安全的公钥加密方案的不可能性(重点))
- [六 RSA加密(重点)](#六 RSA加密(重点))
-
- [6.1 GenRSA(非重点)](#6.1 GenRSA(非重点))
- [6.2 教科书式RSA加密方案(重点)](#6.2 教科书式RSA加密方案(重点))
- [6.3 教科书式RSA加密方案的安全性(重点)](#6.3 教科书式RSA加密方案的安全性(重点))
-
- [6.3.1 不安全的原因(重点)](#6.3.1 不安全的原因(重点))
- [6.3.2 RSA的实验问题(非重点)](#6.3.2 RSA的实验问题(非重点))
- [6.3.3 对RSA的攻击方式(重点)](#6.3.3 对RSA的攻击方式(重点))
- [6.3.4 解决方法(重点)](#6.3.4 解决方法(重点))
- [七 CCA实验和安全性(重点)](#七 CCA实验和安全性(重点))
一 基础知识:四种攻击类型(重点)
- 唯密文攻击(Ciphertext-only attack):COA
- 已知明文(Know-plaintest attack):KPA
- 选择明文攻击(Chosen-plaintext attck):CPA
- 选择密文攻击(Chosen-ciphertext attck):CCA
二 模块化构造知识体系图(重点)
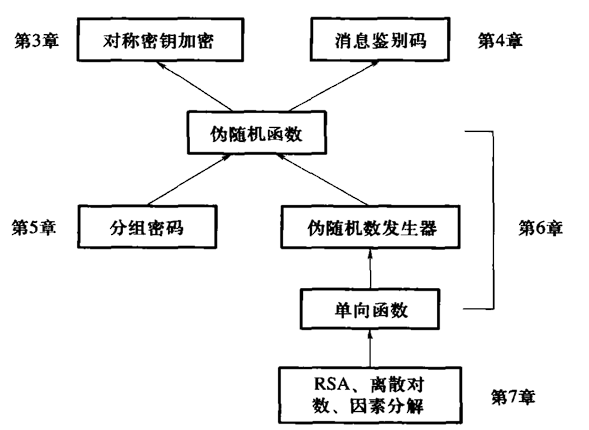
三 公钥加密方案定义
定义 10.1 公钥加密方案是一个概率多项式时间算法(Gen, Enc, Dec)的元组:
(1) 生成密钥算法Gen
Gen用安全参数 1 n 1^n 1n作为输入,输出一对密钥 ( p k , s k ) (pk, sk) (pk,sk)。把 p k pk pk称为公钥,把 s k sk sk称为私钥。为了方便,假设 p k pk pk和 s k sk sk的各自长度至少为 n n n,而且 n n n可由 p k pk pk和 s k sk sk确定。
(2) 加密算法Enc
Enc把公钥 p k pk pk和来自某个明文空间的一个消息 m m m作为输入。输出密文 c c c,记为 c ← Enc p k ( m ) c \leftarrow \text{Enc}_{pk}(m) c←Encpk(m)。
(3) 解密算法Dec
Dec把私钥 s k sk sk和密文 c c c作为输入,输出一个消息 m m m或一个定义为失败的特殊符号 ⊥ \bot ⊥。不失一般性,假设Dec是确定的,记为 m : = Dec s k ( c ) m := \text{Dec}_{sk}(c) m:=Decsk(c)。
满足
Pr [ Dec s k ( Enc p k ( m ) ) = m ] \text{Pr}[\text{Dec}{sk}(\text{Enc}{pk}(m)) = m] Pr[Decsk(Encpk(m))=m]
例外的概率是可忽略的,概率的计算来源于由 Gen ( 1 n ) \text{Gen}(1^n) Gen(1n)输出的 ( p k , s k ) (pk, sk) (pk,sk)和Enc使用的任何随机性。
- 密钥生成算法Gen输出两个密钥。公钥 p k pk pk用于加密,被广泛分发。私钥 s k sk sk解密,由接收方保密保证安全性。
四 公钥加密的CPA不可区分实验(重点)
CPA不可区分实验 PrivK A , Π cpa ( n ) \text{PrivK}_{\mathcal{A},\Pi}^{\text{cpa}}(n) PrivKA,Πcpa(n)
- 执行 G e n ( 1 n ) Gen(1ⁿ) Gen(1n)来获得密钥 ( p k , s k ) (pk, sk) (pk,sk)。
- 敌手A被给予 p k pk pk,并且敌手能够访问 E n c p k ( ⋅ ) Encₚₖ(·) Encpk(⋅)预言机,敌手输出一对相同长度的消息 m 0 , m 1 m₀, m₁ m0,m1(消息必须在与 p k pk pk相关的明文空间中)。
- 随机选择 b ← 0 , 1 b ← {0,1} b←0,1,然后计算出 c ← E n c p k ( m β ) c ← Encₚₖ(mᵦ) c←Encpk(mβ)并且给 A A A。称 c c c是挑战密文。
- A继续使用 E n c p k ( ⋅ ) Encₚₖ(·) Encpk(⋅),输出一位 b ′ b' b′。
- 如果 b = b ′ b = b' b=b′实验输出 1 1 1,否则输出 0 0 0。
定义10.4
如果对于所有概率多项式时间的敌手A存在如下一个可忽略函数negl,满足
Pr [ PubK A , Π cpa ( n ) = 1 ] ⩽ 1 2 + negl ( n ) \text{Pr}\left[\text{PubK}_{A,\Pi}^{\text{cpa}}(n) = 1\right] \leqslant \frac{1}{2} + \text{negl}(n) Pr[PubKA,Πcpa(n)=1]⩽21+negl(n)
则公钥加密方案Π = (Gen, Enc, Dec)在选择明文攻击下具有不可区分加密。
五 完美安全的公钥加密方案的不可能性(重点)
命题 10.5
如果一个公钥加密方案 Π Π Π在窃听者存在情况下具有不可区分加密,则 Π Π Π在选择明文攻击下也具有不可区分加密。
- 完美安全的公钥加密的定义
完美安全的公钥加密需从窃听者视角 定义:要求所有敌手 A A A 满足
Pr [ PubK A , Π eav ( n ) = 1 ] = 1 2 \Pr\left[ \text{PubK}^{\text{eav}}_{A,\Pi}(n) = 1 \right] = \frac{1}{2} Pr[PubKA,Πeav(n)=1]=21
即敌手在窃听者模型下的"优势"为 1 2 \frac{1}{2} 21(相当于随机猜测,无法区分不同密文)。 - 不可能的核心原因:公钥的"公开性"
公钥加密的结构决定了其无法实现完美安全,关键在于公钥是公开的 : 给定公钥 pk \text{pk} pk,密文 c c c 由 c ← Enc pk ( m ) c \leftarrow \text{Enc}_{\text{pk}}(m) c←Encpk(m) 生成( m m m 是明文)。由于公钥公开,敌手可以利用公钥自己加密任意消息 :- 敌手可以遍历所有可能的明文 m m m,计算 Enc pk ( m ) \text{Enc}_{\text{pk}}(m) Encpk(m),并与真实密文 c c c 比较;
- 对于"无限强大"的敌手,总能以概率1 找到与 c c c 匹配的 m m m,从而破解密文。
简言之:公钥的公开性让敌手能"主动生成"密文,破坏了"不可区分加密"的基础(敌手无法区分不同消息的密文,因为自己就能生成对应密文)。
- 最简回答如下:
完美安全的公钥加密要求:在窃听者模型下,敌手无法区分不同密文的加密(即区分概率为1/2,相当于随机猜测)。但公钥加密的公钥是公开的,敌手可利用公钥主动加密任意明文,从而以概率1确定真实明文,这与"不可区分"的核心要求矛盾。因此,完美安全的公钥加密方案不可能存在。
-
与对称密钥加密的对比:对称密钥加密中,完美安全是可能的 (如"一次一密"方案:密钥与消息等长且随机,敌手无法区分不同消息的密文)。 但公钥加密中,无论密钥多长、消息多短,完美安全都不可能------这是核心结论。
-
定理10.6 在窃听者存在情况下,没有一种确定性的公钥加密方案具有不可区分加密。
六 RSA加密(重点)
6.1 GenRSA(非重点)

6.2 教科书式RSA加密方案(重点)
构造方法 10.15
定义公钥加密方案("教科书式RSA"加密方案)如下:
- Gen :输入 1 n 1^n 1n 执行 GenRSA ( 1 n ) (1^n) (1n),获得 ( N , e , d ) (N, e, d) (N,e,d)。其中公钥是 ⟨ N , e ⟩ \langle N, e \rangle ⟨N,e⟩,私钥是 ⟨ N , d ⟩ \langle N, d \rangle ⟨N,d⟩。
- Enc :输入公钥 p k = ⟨ N , e ⟩ pk = \langle N, e \rangle pk=⟨N,e⟩ 和消息 m ∈ Z N ∗ m \in \mathbb{Z}_N^* m∈ZN∗,计算密文 c = [ m e m o d N ] c = [m^e \bmod N] c=[memodN]。
- Dec :输入私钥 s k = ⟨ N , d ⟩ sk = \langle N, d \rangle sk=⟨N,d⟩ 和密文 c ∈ Z N ∗ c \in \mathbb{Z}_N^* c∈ZN∗,计算消息 m = [ c d m o d N ] m = [c^d \bmod N] m=[cdmodN]。
6.3 教科书式RSA加密方案的安全性(重点)
6.3.1 不安全的原因(重点)
- 为什么教科书式RSA加密方案不安全?
- "教科书式RSA"是确定性的,因此是不安全的 。教科书式RSA加密方案不安全的核心原因在于其确定性加密特性,这违反了现代密码学对加密方案的基本安全要求。具体来说,当使用相同的公钥对相同的明文进行加密时,总会产生完全相同的密文,这种可预测性为攻击者提供了多种攻击途径。
- 首先,确定性意味着攻击者可以通过已知明文攻击 轻易验证猜测。其次,确定性加密缺乏语义安全 。语义安全要求即使攻击者获得密文,也无法获得关于明文的任何信息。但教科书式RSA中,相同的明文总是产生相同的密文,使得攻击者能够通过观察密文模式推断明文内容。更严重的是,攻击者还可以通过选择密文攻击利用RSA的代数性质构造特殊密文,从而可能泄露私钥信息。
6.3.2 RSA的实验问题(非重点)
消息编码
- 加密 Z N ∗ \mathbb{Z}_N^* ZN∗中的二进制串元素,令 l = ∣ ∣ N ∣ ∣ l = ||N|| l=∣∣N∣∣,长度为 l − 1 l-1 l−1的二进制串 m m m可视为 Z N \mathbb{Z}_N ZN中的元素,可通过填充方案将各种长度的二进制串编码为 Z N \mathbb{Z}_N ZN中的元素。
理论关注点
- 编码消息 m m m可能不在 Z N ∗ \mathbb{Z}_N^* ZN∗中(如 gcd ( m , N ) ≠ 1 \gcd(m, N) \neq 1 gcd(m,N)=1)
- 即使 m ∉ Z N ∗ m \notin \mathbb{Z}_N^* m∈/ZN∗,解密仍可能成功
- 随机选择的 m m m出现这种情况的概率很小
- 若不分解 N N N,难以发现 m ∈ Z N ∖ Z N ∗ m \in \mathbb{Z}_N \setminus \mathbb{Z}_N^* m∈ZN∖ZN∗
e e e的选择
- 不同 e e e的选择不影响RSA问题的困难性,常见选择: e = 3 e = 3 e=3(仅需两次乘法),需满足 p , q ≠ 1 m o d 3 p, q \neq 1 \bmod 3 p,q=1mod3使得 gcd ( e , ϕ ( N ) ) = 1 \gcd(e, \phi(N)) = 1 gcd(e,ϕ(N))=1, e = 3 e = 3 e=3易受攻击。
- 不建议 选择小的 d d d值加速解密,小范围 d d d易被蛮力搜索,即使 d ≈ N 1 / 4 d \approx N^{1/4} d≈N1/4,仍有恢复 d d d的攻击方法。
中国剩余定理应用
- 接收方可因子分解 N N N,利用中国剩余定理加速解密
- 计算:
m p : = c d m o d p = [ c [ d m o d ( p − 1 ) ] m o d p ] m_p := c^d \bmod p = \left[c^{[d \bmod (p-1)]} \bmod p\right] mp:=cdmodp=[c[dmod(p−1)]modp]
m q : = c d m o d q = [ c [ d m o d ( q − 1 ) ] m o d q ] m_q := c^d \bmod q = \left[c^{[d \bmod (q-1)]} \bmod q\right] mq:=cdmodq=[c[dmod(q−1)]modq] - 结合得到 m ↔ ( m p , m q ) m \leftrightarrow (m_p, m_q) m↔(mp,mq)
- 预计算 [ d m o d ( p − 1 ) ] [d \bmod (p-1)] [dmod(p−1)]和 [ d m o d ( q − 1 ) ] [d \bmod (q-1)] [dmod(q−1)]可进一步优化
- 加速效果:从 8 n 3 8n^3 8n3步降至 2 n 3 2n^3 2n3步(1/4时间)
- 对服务器多解密操作至关重要
6.3.3 对RSA的攻击方式(重点)
- 使用小 e e e加密短消息。
- 恢复明文 m m m的平方改进。
- 公共模攻击 I I I
- 公共模攻击 I I II II
6.3.4 解决方法(重点)
- 增加密钥长度。
- 使用填充方案,如 P K C S # 1 v 1.5 PKCS\#1v1.5 PKCS#1v1.5。
构造方法 10.18
定义GenRSA,并且令 l l l为一个对所有 n n n满足 l ( n ) ≤ 2 n − 2 l(n) \leq 2n-2 l(n)≤2n−2的函数。公钥加密方案如下:
- Gen :输入 1 n 1^n 1n,执行GenRSA ( 1 n ) (1^n) (1n)来获得 ( N , e , d ) (N, e, d) (N,e,d)。输出公钥是 p k = ⟨ N , e ⟩ pk = \langle N, e \rangle pk=⟨N,e⟩,私钥是 s k = ⟨ N , d ⟩ sk = \langle N, d \rangle sk=⟨N,d⟩。
- Enc :输入公钥 p k = ⟨ N , e ⟩ pk = \langle N, e \rangle pk=⟨N,e⟩和消息 m ∈ { 0 , 1 } l ( n ) m \in \{0, 1\}^{l(n)} m∈{0,1}l(n),选择随机串 r ← { 0 , 1 } ∣ ∣ N ∣ ∣ − l ( n ) − 1 r \leftarrow \{0, 1\}^{||N||-l(n)-1} r←{0,1}∣∣N∣∣−l(n)−1,并解释 r ∣ ∣ m r||m r∣∣m为 Z N \mathbb{Z}_N ZN中的元素,输出密文 c : = [ ( r ∣ ∣ m ) e m o d N ] c := [(r||m)^e \bmod N] c:=[(r∣∣m)emodN]。
- Dec :输入私钥 s k = ⟨ N , d ⟩ sk = \langle N, d \rangle sk=⟨N,d⟩和密文 c ∈ Z N ∗ c \in \mathbb{Z}_N^* c∈ZN∗,计算消息 m ^ : = [ c d m o d N ] \hat{m} := [c^d \bmod N] m^:=[cdmodN],并且输出 m ^ \hat{m} m^的低 l ( n ) l(n) l(n)位。
填充的RSA加密方案。
七 CCA实验和安全性(重点)
选择密文攻击不可区分实验 P u b K A , Π c c a ( n ) PubK_{A,Π}^{cca}(n) PubKA,Πcca(n):
(1) 执行Gen ( 1 n ) (1^n) (1n)来获得密钥 ( p k , s k ) (pk, sk) (pk,sk)。
(2) 给敌手 p k pk pk,并且可以使用解密预言机Dec ( ⋅ ) (\cdot) (⋅)。输出一对有相同长度的消息 m 0 , m 1 m_0, m_1 m0,m1。(消息来自于与 p k pk pk相关联的明文空间。)
(3) 选择随机的一个比特 b ← { 0 , 1 } b \leftarrow \{0, 1\} b←{0,1},然后计算出密文 c ← Enc p k ( m b ) c \leftarrow \text{Enc}_{pk}(m_b) c←Encpk(mb),并把密文给 A \mathcal{A} A。
(4) A \mathcal{A} A继续使用解密预言机,但是不能问询 c c c本身的解密。最后, A \mathcal{A} A输出一个比特 b ′ b' b′。
(5) 如果 b ′ = b b' = b b′=b则实验的输出定义为 1 1 1,否则为 0 0 0。
定义 10.24
公钥加密方案 Π = ( Gen , Enc , Dec ) \Pi = (\text{Gen}, \text{Enc}, \text{Dec}) Π=(Gen,Enc,Dec)是选择密文攻击下不可区分加密(或是CCA安全的加密),如果对于所有的概率多项式时间的敌手 A \mathcal{A} A,存在可忽略的函数 negl \text{negl} negl,满足
Pr [ PubK A , Π cca ( n ) = 1 ] ≤ 1 2 + negl ( n ) \Pr[\text{PubK}_{\mathcal{A},\Pi}^{\text{cca}}(n) = 1] \leq \frac{1}{2} + \text{negl}(n) Pr[PubKA,Πcca(n)=1]≤21+negl(n)