算法奇妙屋(二十一)-两个数组或字符串的dp问题(动态规划)

文章目录

• [一. 力扣 [1143. 最长公共子序列](https://leetcode.cn/problems/longest-common-subsequence/description/)](#一. 力扣 1143. 最长公共子序列)
• • [1. 题目解析](#1. 题目解析)
  • [2. 算法原理](#2. 算法原理)
  • [3. 代码](#3. 代码)
• [二. 力扣 [1035. 不相交的线](https://leetcode.cn/problems/uncrossed-lines/description/)](#二. 力扣 1035. 不相交的线)
• • [1. 题目解析](#1. 题目解析)
  • [2. 算法原理](#2. 算法原理)
  • [3. 代码](#3. 代码)
• [三. 力扣 [115. 不同的子序列](https://leetcode.cn/problems/distinct-subsequences/description/)](#三. 力扣 115. 不同的子序列)
• • [1. 题目解析](#1. 题目解析)
  • [2. 算法原理](#2. 算法原理)
  • [3. 代码](#3. 代码)
• [四. 力扣 [44. 通配符匹配](https://leetcode.cn/problems/wildcard-matching/description/)](#四. 力扣 44. 通配符匹配)
• • [1. 题目解析](#1. 题目解析)
  • [2. 算法原理](#2. 算法原理)
  • [3. 代码](#3. 代码)
• [五. 力扣 [10. 正则表达式匹配](https://leetcode.cn/problems/regular-expression-matching/description/)](#五. 力扣 10. 正则表达式匹配)
• • [1. 题目解析](#1. 题目解析)
  • [2. 算法原理](#2. 算法原理)
  • [3. 代码](#3. 代码)
• [六. 力扣 [97. 交错字符串](https://leetcode.cn/problems/interleaving-string/description/)](#六. 力扣 97. 交错字符串)
• • [1. 题目解析](#1. 题目解析)
  • [2. 算法原理](#2. 算法原理)
  • [3. 代码](#3. 代码)
• [七. 力扣 [712. 两个字符串的最小ASCII删除和](https://leetcode.cn/problems/minimum-ascii-delete-sum-for-two-strings/description/)](#七. 力扣 712. 两个字符串的最小ASCII删除和)
• • [1. 题目解析](#1. 题目解析)
  • [2. 算法原理](#2. 算法原理)
  • [3. 代码](#3. 代码)
• [八. 力扣 [718. 最长重复子数组](https://leetcode.cn/problems/maximum-length-of-repeated-subarray/description/)](#八. 力扣 718. 最长重复子数组)
• • [1. 题目解析](#1. 题目解析)
  • [2. 算法原理](#2. 算法原理)
  • [3. 代码](#3. 代码)

一. 力扣 1143. 最长公共子序列

1. 题目解析

题目很好理解, 这里简单提一下

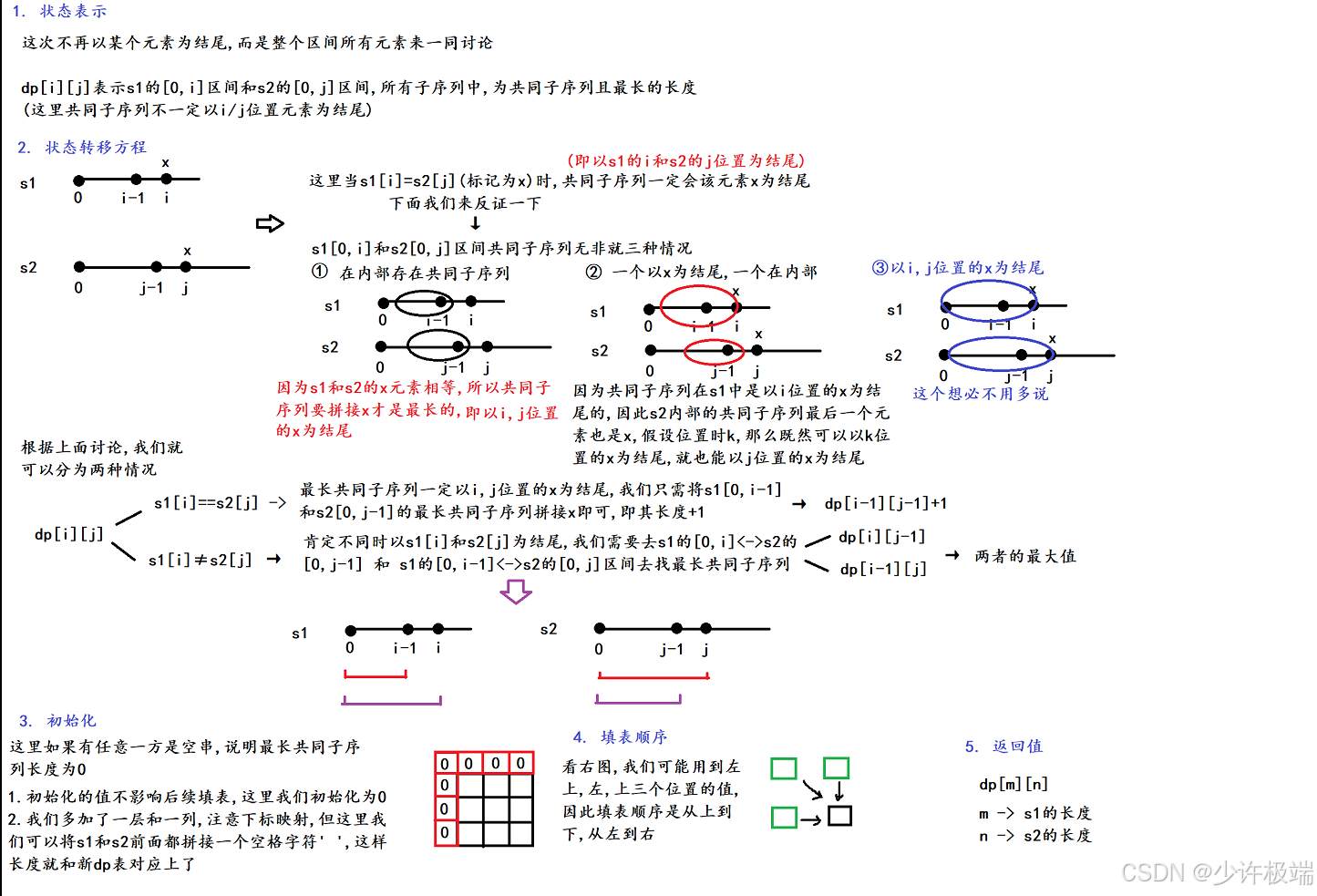
2. 算法原理

细节点很多, 但不用慌, 图解都已点明

3. 代码

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        // 建表/初始化
        int m = text1.length();
        int n = text2.length();
        String s1 = " " + text1;
        String s2 = " " + text2;
        int[][] dp = new int[m + 1][n + 1];
        // 填表
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (s1.charAt(i) == s2.charAt(j)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else {
                    dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
                }
            }
        }
        return dp[m][n];
    }
}

---

二. 力扣 1035. 不相交的线

1. 题目解析

但看题干有点抽象, 但是结合示例之后, 会有新的发现

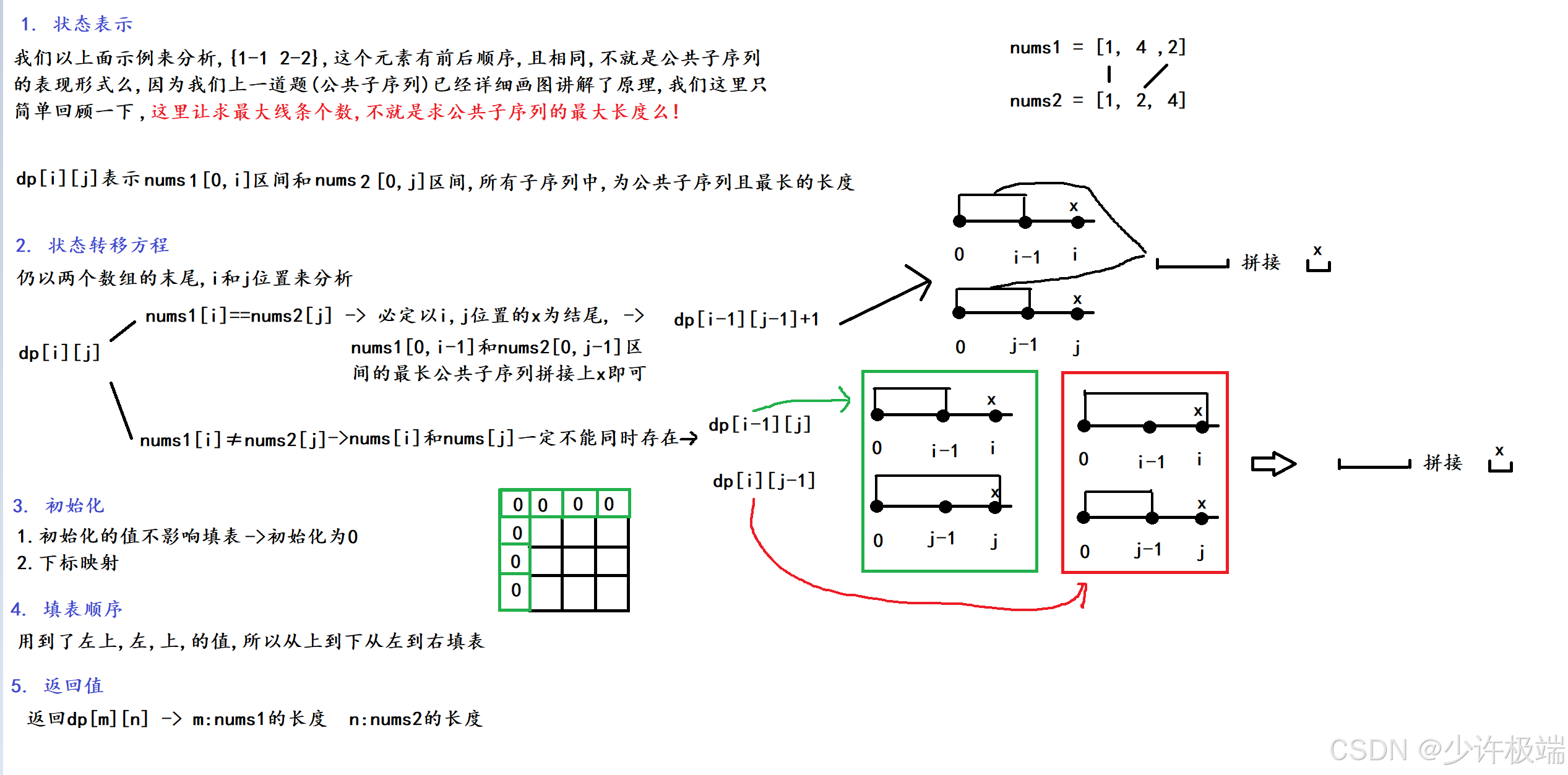
2. 算法原理

原理与上一道题一模一样, 这里带大家简单回忆一下

3. 代码

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        // 建表/初始化
        int m = nums1.length;
        int n = nums2.length;
        int[][] dp = new int[m + 1][n + 1];
        // 填表
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];
    }
}

---

三. 力扣 115. 不同的子序列

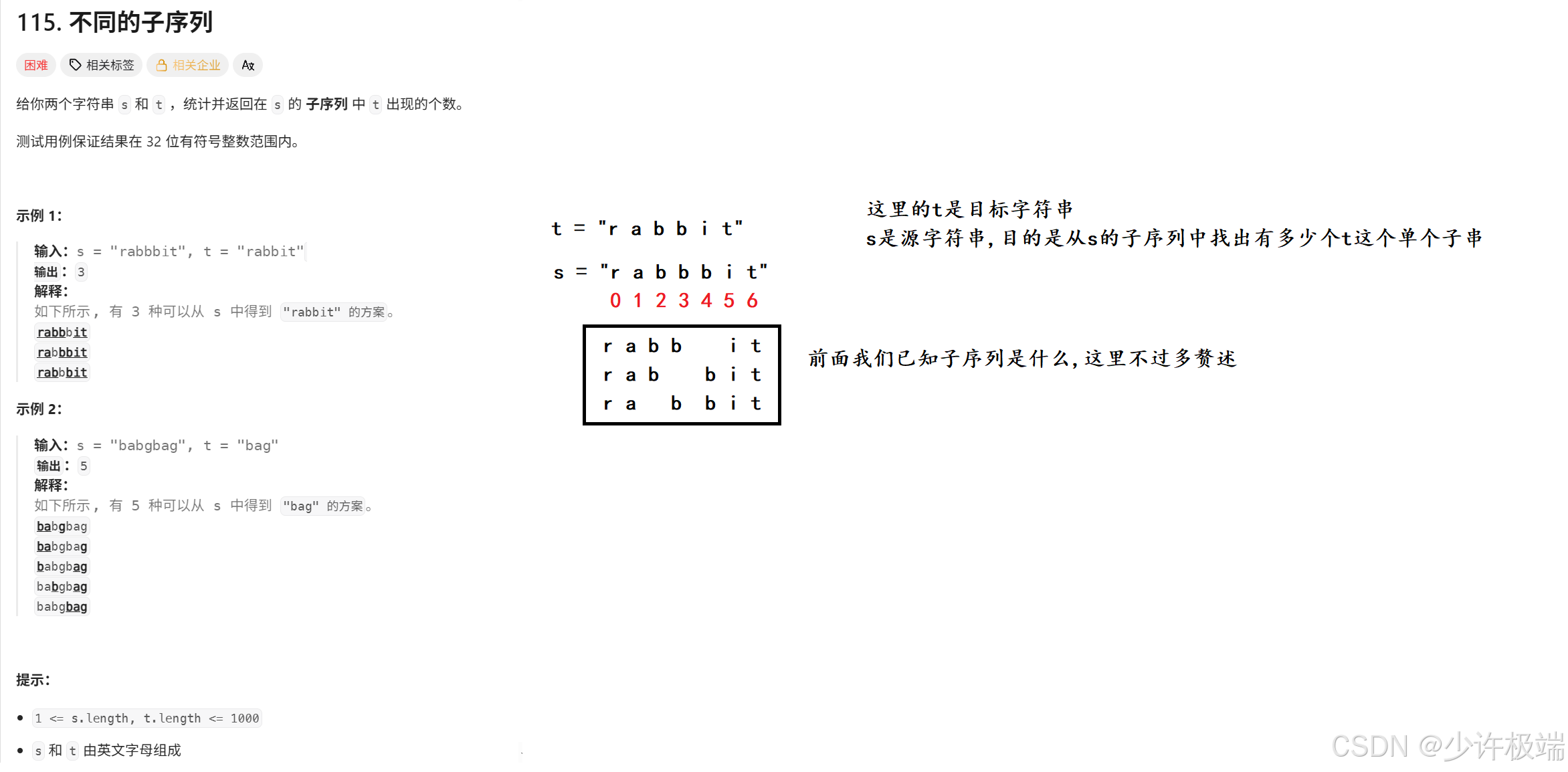
1. 题目解析

题目很短, 也很好理解, 我们简单分析下

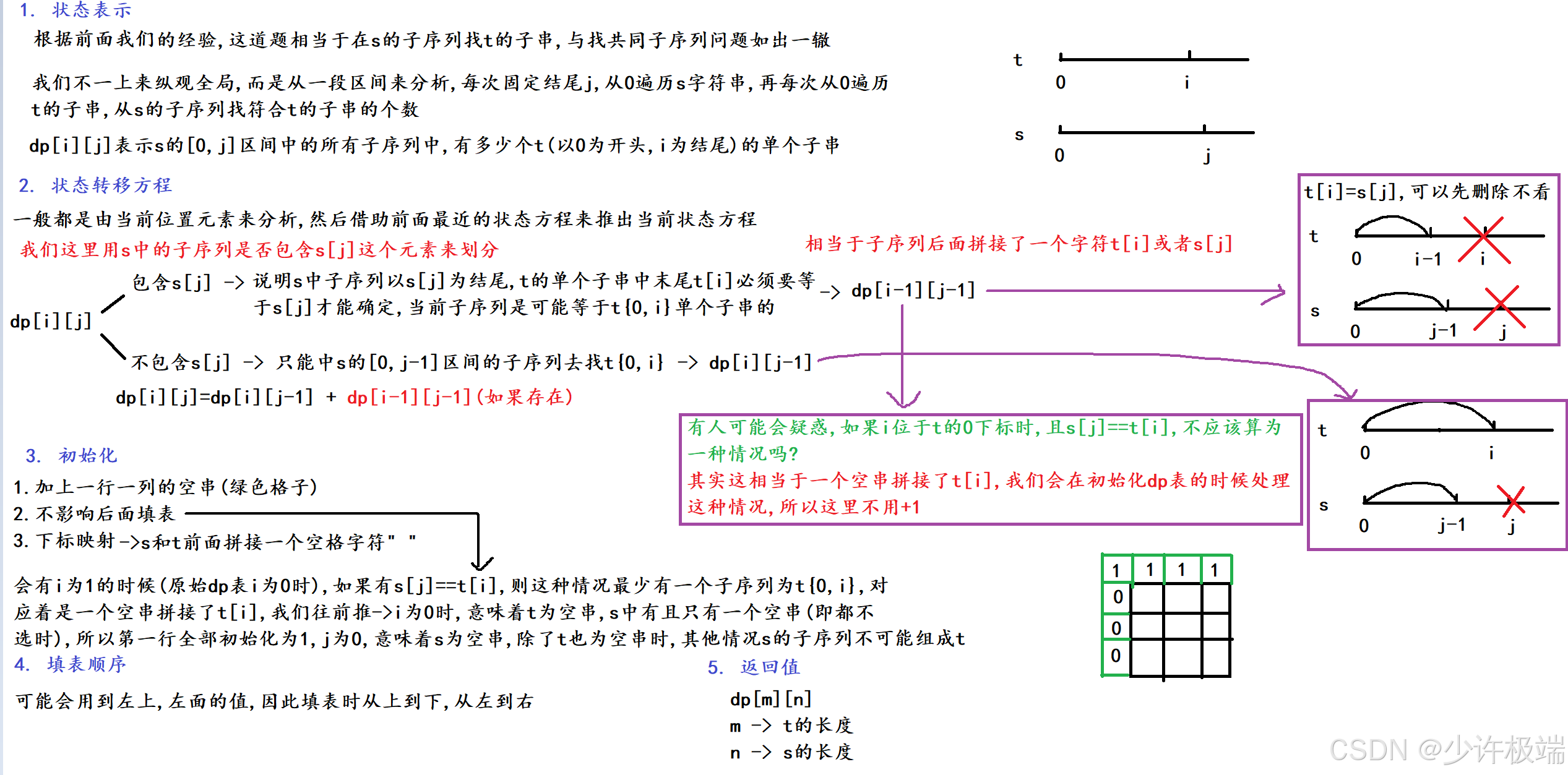
2. 算法原理

这里细节部分较多, 很多原因我们要搞清楚, 这里图解我都做了标记

3. 代码

第一个是对应上面图解的部分
第二个是进一步细分的代码, 即我们不初始化dp表, 直接在填表的时候进行判断, 如果为第一行, 结果是用已经确定的一个子序列+从s的[0,j-1]区间符合条件的子序列个数

class Solution {
    public int numDistinct(String ss, String tt) {
        // 建表
        int n = ss.length();
        int m = tt.length();
        String s = " " + ss;
        String t = " " + tt;
        int[][] dp = new int[m + 1][n + 1];
        // 初始化
        for (int j = 0; j <= n; j++) {
            dp[0][j] = 1;
        }
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                dp[i][j] = t.charAt(i) == s.charAt(j) ? dp[i - 1][j - 1] + dp[i][j - 1] : dp[i][j - 1];
            }
        }
        return dp[m][n];
    }
}

---

class Solution {
    public int numDistinct(String ss, String tt) {
        int n = ss.length();
        int m = tt.length();
        String s = " " + ss;
        String t = " " + tt;
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (i == 1 && t.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i][j - 1] + 1;
                } else {
                    dp[i][j] = t.charAt(i) == s.charAt(j) ? dp[i - 1][j - 1] + dp[i][j - 1] : dp[i][j - 1];
                }
            }
        }
        return dp[m][n];
    }
}

---

四. 力扣 44. 通配符匹配

1. 题目解析

理解特殊字符的含义和题目要求

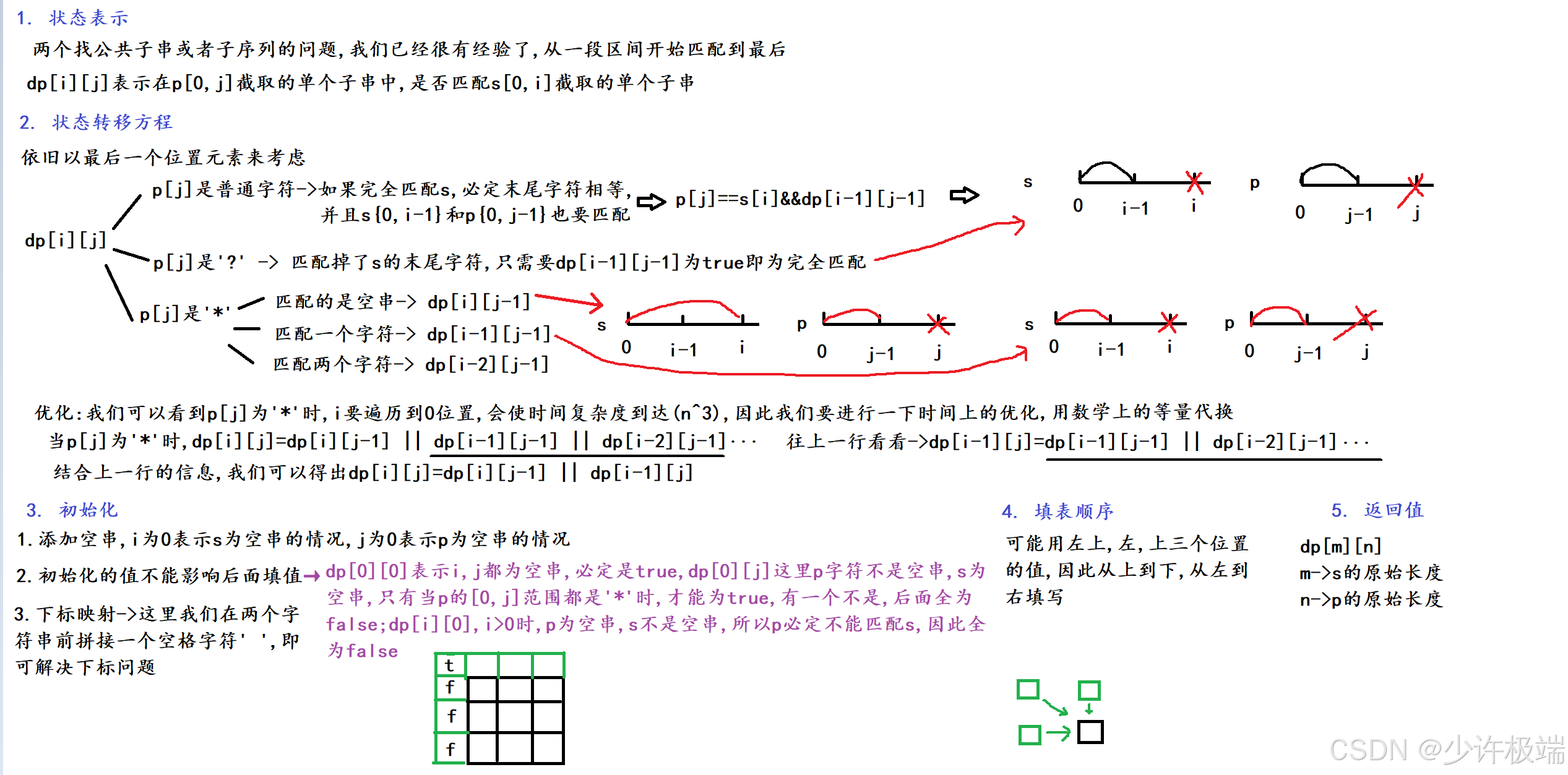
2. 算法原理

细节点较多, 有一些优化, 但整体不算太难

3. 代码

class Solution {
    public boolean isMatch(String ss, String pp) {
        // 建表
        int m = ss.length();
        int n = pp.length();
        String s = " " + ss;
        String p = " " + pp;
        boolean[][] dp = new boolean[m + 1][n + 1];
        // 初始化
        for (int j = 1; j <= n; j++) {
            if (p.charAt(j) == '*') {
                dp[0][j] = true;
            }else {
                break;
            }
        }
        dp[0][0] = true;
        // 填表
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                char ch = p.charAt(j);
                if (ch == '?' || ch == s.charAt(i)) {
                    dp[i][j] = dp[i - 1][j - 1];
                }else if (ch == '*') {
                    dp[i][j] = dp[i][j - 1] || dp[i - 1][j];
                }
            }
        }
        return dp[m][n];
    }
}

---

五. 力扣 10. 正则表达式匹配

1. 题目解析

题目细节较多, 和上一道题差不多

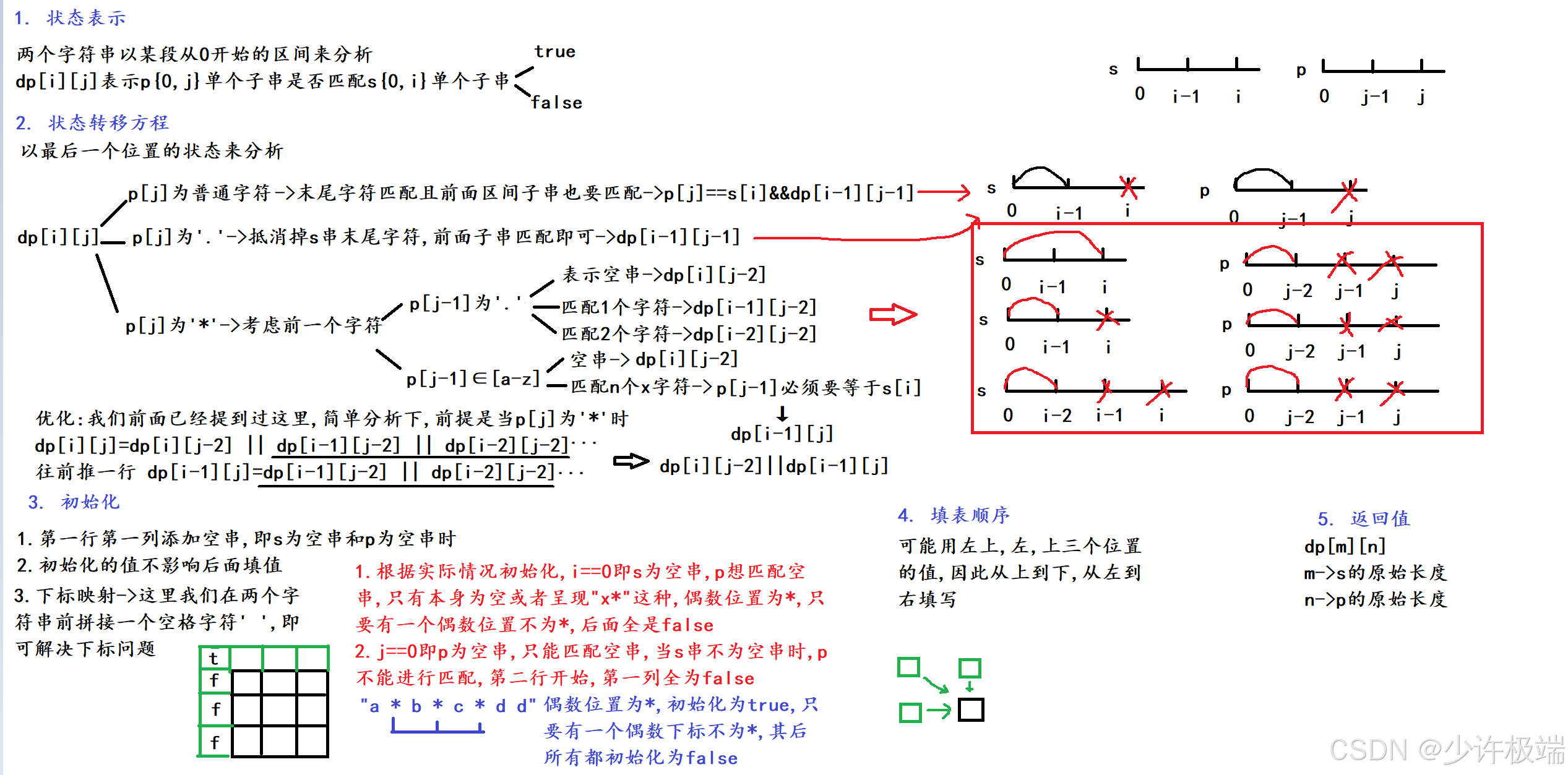
2. 算法原理

原理与上一道题差不多, 细节方面稍有不同

3. 代码

class Solution {
    public boolean isMatch(String ss, String pp) {
        // 建表
        int m = ss.length();
        int n = pp.length();
        char[] s = (" " + ss).toCharArray();
        char[] p = (" " + pp).toCharArray();
        boolean[][] dp = new boolean[m + 1][n + 1];
        // 初始化
        dp[0][0] = true;
        for (int j = 2; j <= n; j += 2) {
            if (p[j] == '*') {
                dp[0][j] = true;
            } else {
                break;
            }
        }
        // 填表
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (p[j] != '*' && (s[i] == p[j] || p[j] == '.') && dp[i - 1][j - 1]) {
                    dp[i][j] = true;
                } else if (p[j] == '*') {
                    if (dp[i][j - 2] || (p[j - 1] == s[i] || p[j - 1] == '.') && dp[i - 1][j]) {
                        dp[i][j] = true;
                    }
                }
            }
        }
        return dp[m][n];
    }
}

---

六. 力扣 97. 交错字符串

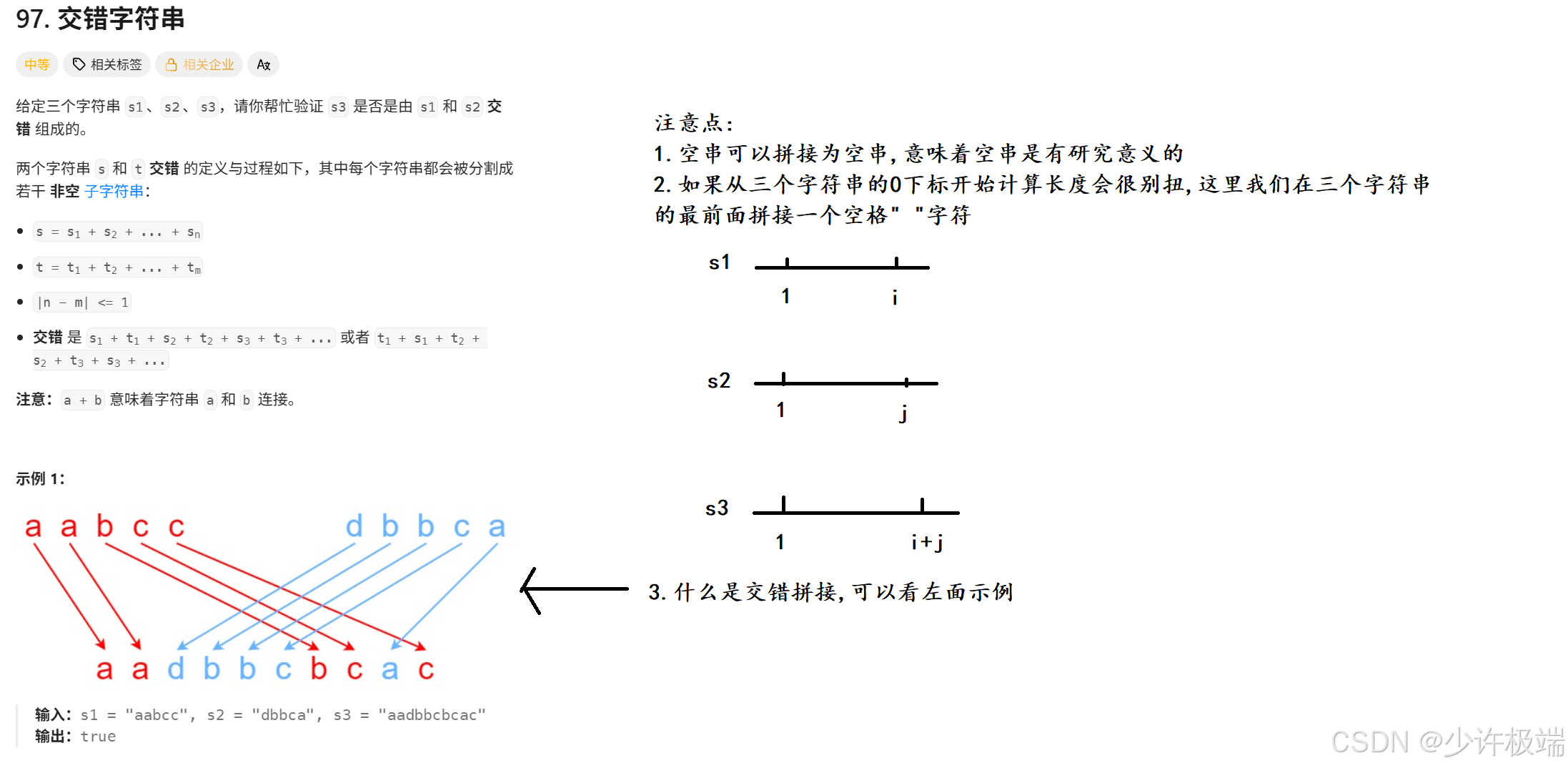
1. 题目解析

只看题目感觉有点难, 但是进行分析时发现还是较容易的

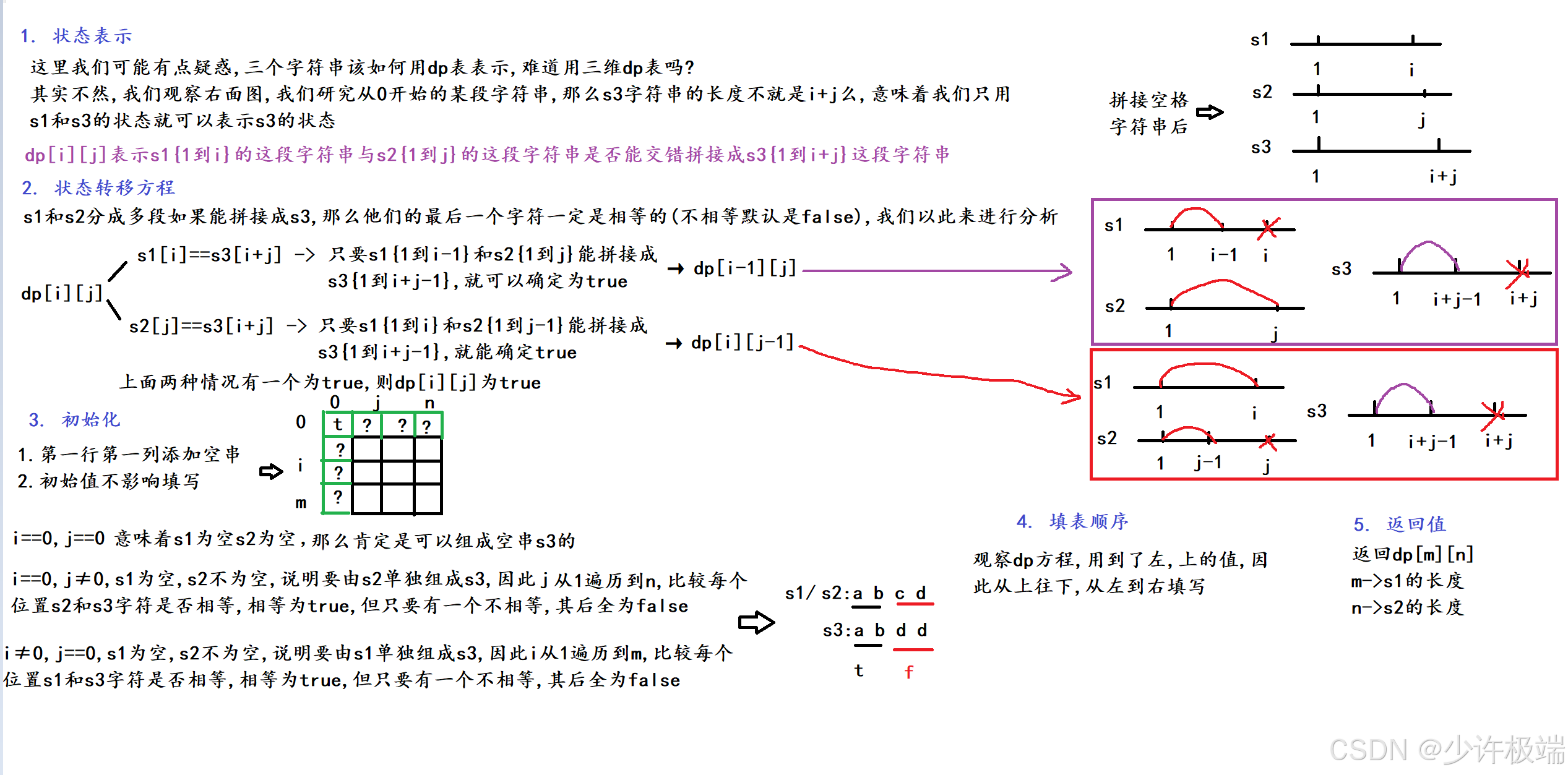
2. 算法原理

需要注意, 我们这里考虑的都是三个字符串前面拼接上空格后的状态

3. 代码

class Solution {
    public boolean isInterleave(String s11, String s22, String s33) {
        // 建表, 特殊处理
        int m = s11.length();
        int n = s22.length();
        if (m + n != s33.length()) {
            return false;
        }
        char[] s1 = (" " + s11).toCharArray();
        char[] s2 = (" " + s22).toCharArray();
        char[] s3 = (" " + s33).toCharArray();
        boolean[][] dp = new boolean[m + 1][n + 1];
        // 初始化
        dp[0][0] = true;
        for (int i = 1; i <= m; i++) {
            if (s1[i] == s3[i]) {
                dp[i][0] = true;
            }else {
                break;
            }
        }
        for (int j = 1; j <= n; j++) {
            if (s2[j] == s3[j]) {
                dp[0][j] = true;
            }else {
                break;
            }
        }
        // 填表
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (s1[i] == s3[i + j] && dp[i - 1][j] || s2[j] == s3[i + j] && dp[i][j - 1]) {
                    dp[i][j] = true;
                }
            }
        }
        return dp[m][n];
    }
}

---

七. 力扣 712. 两个字符串的最小ASCII删除和

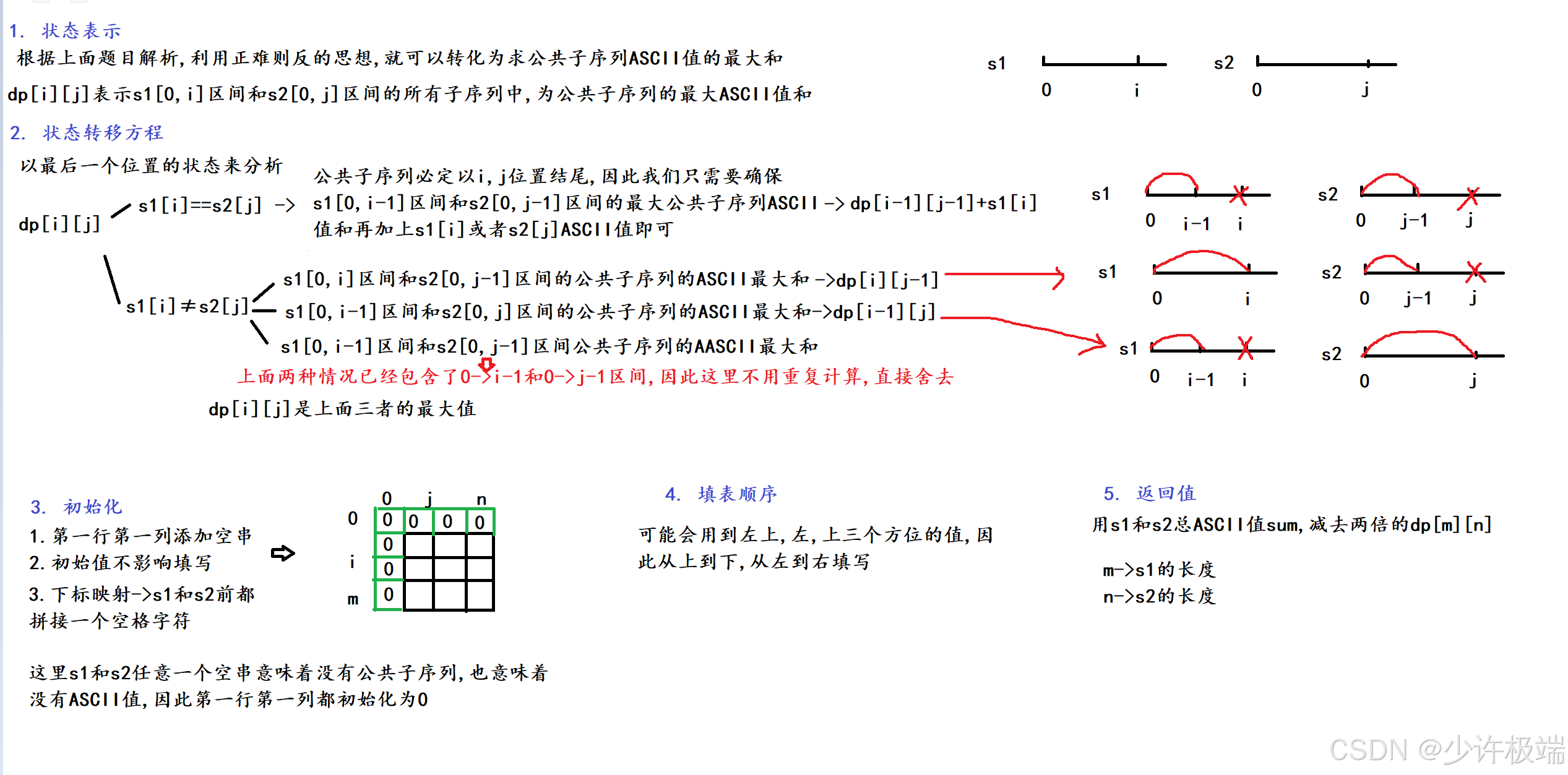
1. 题目解析

2. 算法原理

3. 代码

class Solution {
    public int minimumDeleteSum(String s11, String s22) {
        // 建表,初始化
        int m = s11.length();
        int n = s22.length();
        char[] s1 = (" " + s11).toCharArray();
        char[] s2 = (" " + s22).toCharArray();
        int[][] dp = new int[m + 1][n + 1];
        // 填表
        for (int i = 1; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                if (s1[i] == s2[j]) {
                    dp[i][j] = dp[i - 1][j - 1] + s1[i];
                }
                dp[i][j] = Math.max(dp[i][j], Math.max(dp[i][j - 1], dp[i - 1][j]));
            }
        }
        // 返回结果
        int sum = 0;
        for (int i = 1; i <= m; i++) {
            sum += s1[i];
        }
        for (int j = 1; j <= n; j++) {
            sum += s2[j];
        }
        return sum - 2 * dp[m][n];
    }
}

---

八. 力扣 718. 最长重复子数组

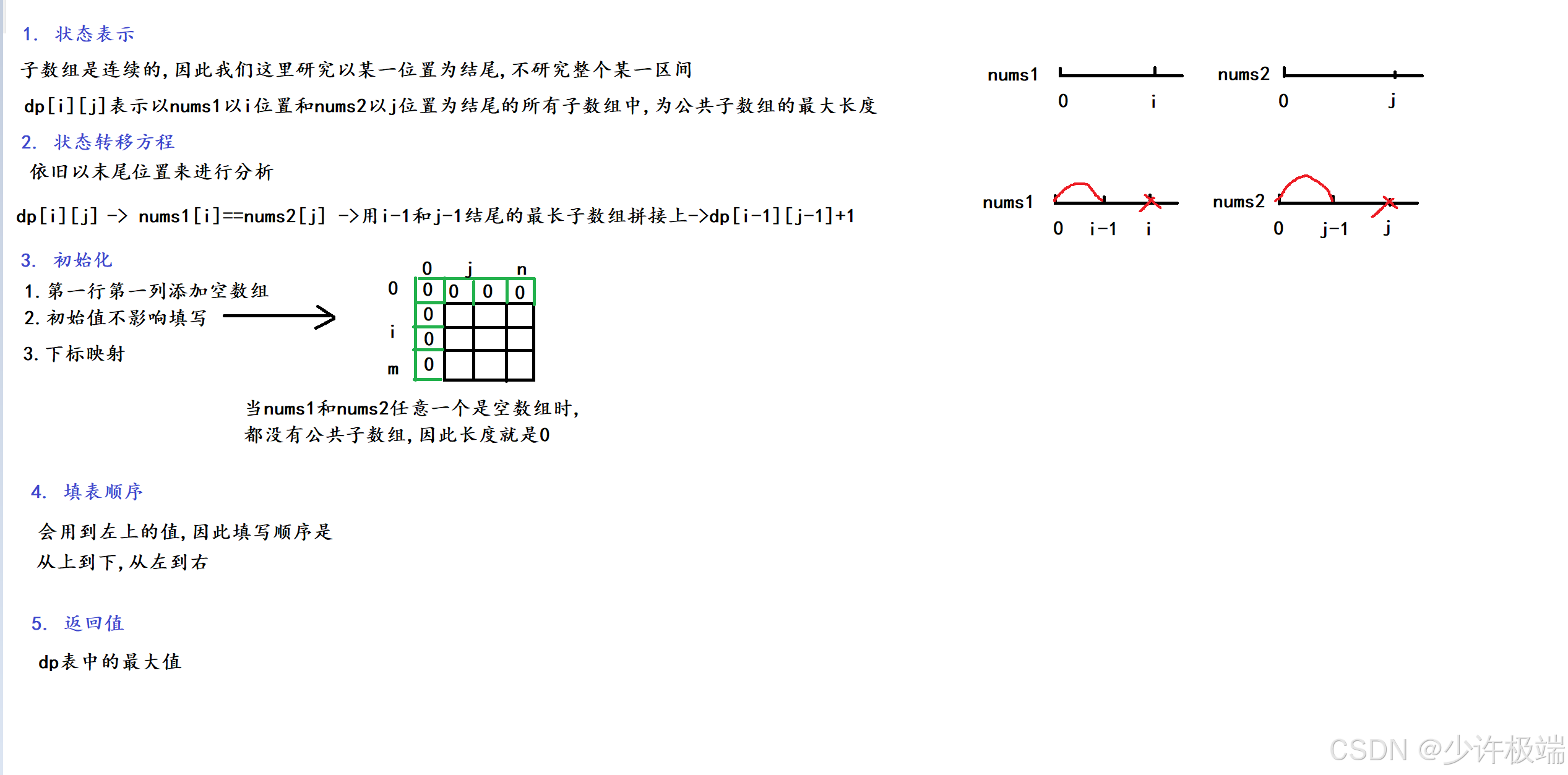
1. 题目解析

题意很好理解, 直接看示例即可, 要注意的是子序列和子数组的关系

2. 算法原理

3. 代码

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        // 建表,初始化
        int m = nums1.length;
        int n = nums2.length;
        int[][] dp = new int[m + 1][n + 1];
        //填表
        int ret = 0;
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                    ret = Math.max(ret, dp[i][j]);
                }
            }
        }
        return ret;
    }
}