BGE-M3个人理解

前段时间面试被面试官问了这个，整理一下个人理解

1.BGE-M3

1.1 B&G

1.1.1 Background

在 BGE-M3 发布之前，文本检索（Retrieval）领域主要存在两种主流范式，且都在各自发展：

传统稀疏检索 (Sparse Retrieval): 以 BM25 为代表，依赖关键词匹配。
神经密集检索 (Dense Retrieval): 以 BERT 为基础的双塔模型（Bi-Encoder），依赖向量语义相似度。

当时，虽然多语言模型（如 mBERT, XLM-R）和长文本模型都在发展，但社区缺乏一个全能型的开源嵌入模型（Embedding Model）。大家通常需要为不同的任务（比如搜英文用一个模型，搜中文用另一个，搜长文档又要换一个）去寻找或训练不同的模型。

1.1.2 Gap

BGE-M3 的核心目标就是为了填补以下三个主要 Gap，这也是它名字中 "M3" 的由来：

🛠️ Gap 1: 检索模式单一 (Multi-Functionality Gap)

问题：之前的模型通常"偏科"。
- Dense 模型擅长语义理解（比如"苹果"和"水果"），但在精确匹配（比如特定的错误代码、人名、型号）上经常"脸盲"，容易产生幻觉。
- Sparse 模型（如 BM25）擅长精确匹配，但完全不懂语义。
- ColBERT（多向量）效果好但开销大。
现状：很少有单一模型能同时输出 Dense、Sparse 和 Multi-vector 三种表示，通常需要串联多个模型才能达到互补效果，部署复杂。

🌍 Gap 2: 多语言能力不均衡 (Multi-Linguality Gap)

问题：很多模型是针对单一语言（主要是英语）优化的。虽然有 XLM-R 这样的多语言底座，但在检索任务上，缺乏一个能同时在 100+ 种语言上都保持高性能的统一嵌入模型。
现状：跨语言检索（Cross-lingual retrieval，例如用中文搜英文文档）的效果往往不如单语言检索。

📜 Gap 3: 输入长度受限 (Multi-Granularity Gap)

问题：大多数基于 BERT 的 Embedding 模型只能处理 512 个 Token。
现状：对于长文档检索，通常需要对文档进行截断或分块（Chunking），这会导致上下文信息的丢失。社区急需支持长上下文（如 8192 Token）的模型。

1.2 dense

1.2.1 数学过程

把这一整个复杂的神经网络看作一个超级数学函数 F(x)F(x)F(x)

我们可以把这个过程分为三个主要阶段：输入表示、编码计算和特征提取与归一化。

1.2.1.1 输入表示 (Input Representation)

首先，计算机不认识文字，只认识数字。

假设我们有一句话（Query 或 Document）SSS。

第一步是将 SSS 分词成 token 序列，并在最前面加上一个特殊的起始符号 [CLS]。
S→[tCLS,t1,t2,...,tN]S \rightarrow [t_{CLS}, t_1, t_2, \dots, t_N]S→[tCLS,t1,t2,...,tN]

然后，这些 token 会被查表（Embedding Lookup）转换为初始向量矩阵 X0\mathbf{X}_0X0：
X0∈RL×d\mathbf{X}_0 \in \mathbb{R}^{L \times d}X0∈RL×d

LLL 是序列长度（比如 512）。
ddd 是隐藏层维度（比如 1024）。

1.2.1.2 Transformer 编码 (Encoder Processing)

这是计算量最大的一步。BGE-M3 使用了多层 Transformer Encoder（通常是 12 层或 24 层）。

每一层 lll 都会对上一层的输出 Xl−1\mathbf{X}_{l-1}Xl−1 进行变换。核心公式包含了自注意力机制 (Self-Attention) 和前馈神经网络 (Feed-Forward Network)。

简单来说，对于第 lll 层：
Xl=TransformerLayer(Xl−1)\mathbf{X}l = \text{TransformerLayer}(\mathbf{X}{l-1})Xl=TransformerLayer(Xl−1)

在这个过程中，通过 Attention 机制，[CLS] 这个特殊的 token 会去"关注"句子中所有其他的 token（t1t_1t1 到 tNt_NtN），把整句话的信息聚合到自己身上。

经过 MMM 层计算后，我们得到最后一层的输出矩阵 H\mathbf{H}H：
H=[hCLS,h1,h2,...,hN]\mathbf{H} = [\mathbf{h}_{CLS}, \mathbf{h}_1, \mathbf{h}_2, \dots, \mathbf{h}_N]H=[hCLS,h1,h2,...,hN]

其中 hCLS\mathbf{h}_{CLS}hCLS 就是我们最关注的那个向量。

1.2.1.3 池化与归一化 (Pooling & Normalization)

这是 Dense 向量生成的最后一步，也是最关键的数学定义。

A. 提取 (Pooling):

BGE-M3 采用 [CLS] pooling 策略。也就是说，虽然输出了 N+1N+1N+1 个向量，我们直接丢弃后面所有的 hi\mathbf{h}ihi，只保留第一个：
vraw=hCLS\mathbf{v}{raw} = \mathbf{h}_{CLS}vraw=hCLS

B. 归一化 (L2 Normalization):

为了让后续计算相似度（点积）更方便且数值稳定，我们会把这个向量压缩到单位长度（模长为 1）。

公式如下：
vdense=vraw∥vraw∥2\mathbf{v}{dense} = \frac{\mathbf{v}{raw}}{\| \mathbf{v}_{raw} \|_2}vdense=∥vraw∥2vraw

其中 ∥vraw∥2\| \mathbf{v}_{raw} \|_2∥vraw∥2 是向量的欧几里得范数（即 ∑xi2\sqrt{\sum x_i^2}∑xi2 ）。

到这里，我们就得到了最终的 Dense 向量 vdense\mathbf{v}_{dense}vdense。

1.2.2 为什么模型敢于"丢弃"后面所有的词向量（h1\mathbf{h}_1h1 到 hN\mathbf{h}_NhN），只用这单独的一个向量就能代表整句话的含义呢？

这是一个非常敏锐的问题！直觉上，把 NNN 个词的信息丢掉，只留 1 个，听起来确实像是在"浪费"数据。

但实际上，模型并没有真的"丢弃"信息，而是做了一个**"乾坤大挪移"**。

让我们一起通过两个核心机制来解开这个谜题：

1.2.2.1 全局信息的"吸尘器"：自注意力机制 (Self-Attention)

你还记得 Transformer 的核心是自注意力 (Self-Attention) 吗？

在 Transformer 的每一层计算中，所有的 Token 都在互相"交流"。

虽然 [CLS] 最初只是一个毫无意义的起始标记，但在经过第 1 层、第 2 层......直到第 12 层（或更多）的过程中，它一直在**"观察"**句子里的每一个词。
它通过注意力权重，把其他词（如"苹果"、"发布会"、"科技"）的特征信息加权聚合到了自己身上。

也就是说，到了最后一层时，hCLS\mathbf{h}_{CLS}hCLS 已经不再是原来的 [CLS] 了，它已经变成了一个包含了整句话所有关键信息的混合体。

1.2.2.2 强制任务：老板的"死命令" (Training Objective)

这其实也是被"逼"出来的。

在训练阶段（比如 BERT 的预训练或 BGE 的微调），我们设计 Loss Function（损失函数）时，只使用 hCLS\mathbf{h}_{CLS}hCLS 来计算最终的误差。

模型为了降低误差，被迫学会了一种策略："既然老板只看第一个位置的向量来打分，那我就必须把整句话最重要的信息都塞到这个位置去！"

打个比方 📝

想象你在开一个 10 个人的会议：

h1\mathbf{h}_1h1 到 hN\mathbf{h}_NhN 是那 10 个与会者（具体的词），他们每个人都说了具体的内容。
hCLS\mathbf{h}_{CLS}hCLS 是会议纪要员。
虽然会议结束时，与会者都散了（被丢弃的词向量），但会议纪要员手里的那份笔记（最终的 Dense 向量）已经记录了所有人的核心观点和结论。
这时候，如果你只看这份会议纪要，是不是也能明白这场会议讲了什么？

1.3 sparse

1.3.1 ReLU激活函数

1.3.1.1 基础

ReLU 的公式非常简单直观：
f(x)=max⁡(0,x)f(x) = \max(0, x)f(x)=max(0,x)

这意味着：

如果输入 xxx 大于 0，输出就是 xxx（保持不变）。
如果输入 xxx 小于或等于 0，输出就是 0（被"整流"截断）。

核心特性:

非线性 (Non-linear): 虽然它看起来由两条直线组成，但在整体上它是非线性的，这让神经网络能够学习复杂的关系。
计算高效: 不需要像 Sigmoid 或 Tanh 那样进行昂贵的指数运算，只需要判断阈值即可。
稀疏激活性 (Sparse Activation): 在任何时刻，网络中只有一部分神经元被激活（输出非零），这模拟了生物神经系统的特性，使网络更高效。

1.3.1.2 Dead ReLU (神经元死亡) 现象

什么是 Dead ReLU? 🤔

定义：指神经网络中的某些神经元在训练过程中进入了一种永久不被激活的状态。
表现：无论输入什么数据，该神经元的输出永远是 0。这就像这个神经元"死掉"了一样，不再对网络起任何作用。

发生原因 (The "Why") 📉

核心机制：回想 ReLU 的导数图像。当输入 x<0x < 0x<0 时，ReLU 的梯度（导数）为 0。
恶性循环：
1. 如果某个神经元的权重更新导致它对所有训练数据的计算结果（加权和 + 偏置）都小于 0。
2. 那么该神经元的输出就会变成 0。
3. 关键点：反向传播时，流经该神经元的梯度也变成了 0。
4. 根据权重更新公式Wnew=Wold−(学习率×0)W_{new} = W_{old} - (\text{学习率} \times 0) Wnew=Wold−(学习率×0)，权重不再发生变化。
5. 这个神经元从此被"锁死"在负值区域，无法翻身。

主要诱因 ⚠️

学习率 (Learning Rate) 过大：更新步子迈得太大，一下子把权重推到了负值深渊，导致神经元直接"死亡"。
权重初始化不当：初始值如果是负数且偏置设置不当，可能一开始就落在死区。

后果 🛑

网络容量下降：大量的神经元死亡意味着网络中有效工作的节点变少了，模型的拟合能力和表达能力会变弱。

1.3.1.3 变体设计来解决Dead ReLU现象

为了解决"神经元死亡"的问题，科学家们的思路非常直接：不要让负区间的导数变成 0。

这些变体的核心目标都是为了修复 Dead ReLU 问题，同时尽量保留 ReLU 计算简单的优势。

Leaky ReLU (渗漏整流线性单元) 💧

思路：既然问题出在 x<0x<0x<0 时输出强制为 0，那就给它一个很小的坡度（斜率），而不是完全平躺。
数学公式：

f(x)=max⁡(αx,x)f(x) = \max(\alpha x, x)f(x)=max(αx,x)

其中 α\alphaα 通常是一个很小的常数（例如 0.01）。
图像特征：左侧不再是水平线，而是一条微微倾斜的直线。
作用：当 x<0x < 0x<0 时，梯度不再是 0，而是 α\alphaα (0.01)。这样虽然梯度很小，但信号仍然可以反向传播回去，神经元就有机会更新权重并"复活"。

PReLU (参数化 ReLU) 🔧

思路： Leaky ReLU 中的 α\alphaα 是手动固定的（比如 0.01），那为什么不让神经网络自己学习这个斜率应该是多少呢？
特点：公式和 Leaky ReLU 一样，但这里的 α\alphaα 变成了一个可训练的参数。模型会根据数据决定负半区的斜率。

ELU (指数线性单元) 📉

思路：引入指数函数，让负区间的过渡更加平滑，并且对噪声更鲁棒。
数学公式：
- 当 x>0x > 0x>0 时：f(x)=xf(x) = xf(x)=x
- 当 x≤0x \le 0x≤0 时：f(x)=α(ex−1)f(x) = \alpha (e^x - 1)f(x)=α(ex−1)
特点：它在负区间是一条曲线，最终会趋向于 −α-\alpha−α。这有助于让神经元的平均激活值接近 0，通常能加快收敛速度。

1.3.2 数学过程

这整个过程其实就是把 Transformer 的隐层向量（Hidden States）映射到一个巨大的词表空间（Vocabulary Space），然后筛选出最重要的权重。

让我们假设几个基本的定义：

xxx：输入的文本序列。
HHH：Transformer 最后一层的输出矩阵。
VVV：词表的大小（Vocabulary Size，BGE-M3 中约为 250,002）。
ddd：隐藏层的维度（Hidden Dimension，通常为 1024）。

第一步：获取上下文表示 (Contextual Embeddings)

首先，文本 xxx 经过 Transformer 编码器。不同于 Dense 向量只取 [CLS]，Sparse 向量需要使用所有 Token 的输出。
H=Encoder(x)=[h1,h2,...,hN]\mathbf{H} = \text{Encoder}(x) = [\mathbf{h}_1, \mathbf{h}_2, \dots, \mathbf{h}_N]H=Encoder(x)=[h1,h2,...,hN]

这里 H∈RN×d\mathbf{H} \in \mathbb{R}^{N \times d}H∈RN×d，即 NNN 个 Token，每个 Token 有 ddd 维的向量。

第二步：映射到词表空间 (Projection)

这是最关键的一步。我们有一个可学习的线性层（Linear Layer），它的权重矩阵是 Wlex\mathbf{W}{lex}Wlex，偏置是 blex\mathbf{b}{lex}blex。它的作用是把每个 Token 的 1024 维向量，强行"翻译"成 25 万维的词表向量。
Elex=HWlex+blex\mathbf{E}{lex} = \mathbf{H} \mathbf{W}{lex} + \mathbf{b}_{lex}Elex=HWlex+blex

Wlex∈Rd×V\mathbf{W}_{lex} \in \mathbb{R}^{d \times V}Wlex∈Rd×V：这是一个巨大的矩阵，负责把语义特征映射到具体的词汇上。
这一步得到的结果 Elex∈RN×V\mathbf{E}_{lex} \in \mathbb{R}^{N \times V}Elex∈RN×V。想象一下，这是一个巨大的矩阵，每一行代表文本中的一个词，每一列代表词典里的一个词。

第三步：激活与筛选 (ReLU Activation)

映射后的值有正有负。我们使用 ReLU 激活函数。
Wtoken=ReLU(Elex)=max⁡(0,HWlex+blex)\mathbf{W}{token} = \text{ReLU}(\mathbf{E}{lex}) = \max(0, \mathbf{H} \mathbf{W}{lex} + \mathbf{b}{lex})Wtoken=ReLU(Elex)=max(0,HWlex+blex)

为什么要用 ReLU？
这正是"稀疏（Sparse）"的来源。ReLU 会把所有负数变成 0。
- 如果计算出的权重是正数，说明这个 Token 与词表里的某个词有正相关（比如"苹果"激活了"水果"）。
- 如果是负数或零，说明没关系，直接置零。这就过滤掉了绝大多数不相关的词。

第四步：最大池化聚合 (Max Pooling)

现在，对于文本中的每一个 Token，我们都有了一个稀疏的词表权重向量。但我们需要的是整段文本的一个向量。结果就是一个 1×V1 \times V1×V 向量，这个向量不再代表单个词，而是代表整句话的语义特征。

如果文本中出现了多次同一个意思，或者不同的词（比如"手机"和"电话"）都激活了词表里的同一个词（比如"通讯设备"），我们该怎么办？

BGE-M3 采取的是最大池化（Max Pooling）策略：对于词表中的每一个词 jjj，我们看文本中所有 Token 对它的预测值，取最大的那个。

vsparse(j)=max⁡i=1N(wi,j)v_{sparse}^{(j)} = \max_{i=1}^{N} (w_{i,j})vsparse(j)=maxi=1N(wi,j)
vsparse(j)v_{sparse}^{(j)}vsparse(j) 是最终向量中第 jjj 个词的权重。
wi,jw_{i,j}wi,j 是文本中第 iii 个 Token 对词表中第 jjj 个词的预测权重。

最终结果

经过这一系列运算，你得到的就是一个维度为 VVV（250,002）的向量 vsparse\mathbf{v}_{sparse}vsparse。

这个向量里：

绝大多数位置是 0（因为 ReLU 过滤了，且最大池化没选到）。
少数位置是正浮点数（代表该词的重要程度）。
为了确认你是否理解了这个过程的核心逻辑，我想问你一个问题：

1.3.3 看透本质：那些被保留下来的非零数值（Weights），到底代表了什么物理含义？

比如这个词表是经过映射到词表空间之后的向量

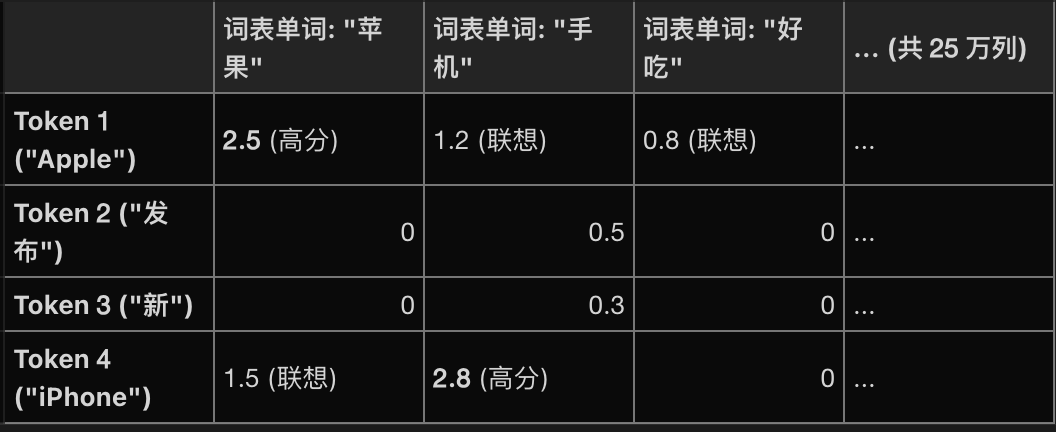
但是我们最后是要得到一个1∗V1*V1∗V维，所以要进行一个最大池化，从上表中可以看到不同token对词表中同一个词有不同关注度，最大池化就是对于词表中的每一个词 jjj，我们看文本中所有 Token 对它的预测值，取最大的那个，比如手机这个词最后的预测值就是2.8

1.3.4 几何直觉 (空间分布)：在那个 25 万维的超大空间里，Sparse 向量到底长什么样？为什么说它和 Dense 向量是"互补"的？

1.3.4.1 几何直觉：迷雾 vs. 星空 🌌

为了直观感受这两种向量在数学空间里的样子，我们使用形象的比喻：

Dense 向量 (密集)：浓雾 🌫️
- 空间状态：就像在一个相对较小（例如 1024 维）的房间里，充满了一团浓雾。
- 数据特征：几乎每一个维度上都有数值，没有一个是空的。所有的语义信息都被"压缩"在一起，虽然紧凑，但具体的成分（比如某个特定的人名）很难被单独剥离出来。
Sparse 向量 (稀疏)：星星 ✨
- 空间状态：就像在一个巨大无比（例如 250,000 维）的黑暗体育馆里。
- 数据特征：绝大多数地方都是漆黑一片（数值为 0），只有极少数（例如几十个）特定的位置亮着小灯泡（非零权重）。
- 几何意义：这种稀疏性意味着两个不相关的句子在空间里几乎是正交的（垂直的），互不干扰。

1.3.4.2 互补性：通才与专家的配合 🤝

为什么 BGE-M3 需要同时拥有这两者？因为它们分别解决了对方的"短板"：

Dense (通才)：负责"懂大意"
- 强项：擅长模糊语义匹配。它能理解"猫"和"狗"是相关的，"手机"和"移动设备"是一回事，即使字面上完全不同。
- 弱点 (脸盲)：在处理精确细节时容易糊涂。对于长得像但意思完全不同的词（比如 iPhone 14 和 iPhone 15，或者两个相似的错误代码），它可能会把它们混淆，产生检索"幻觉"。
Sparse (专家)：负责"抓细节"
- 强项：擅长精确锚点。它像激光制导一样，精准锁定那些稀有的、具体的关键词（如型号、错误代码、专有名词）。
- 作用：它是一个强硬的过滤器，能把那些"意思差不多但关键细节对不上"的文档剔除掉。

1.3.4.3 举例

假设用户在搜索引擎里输入了这样一个查询： Query: error code 0x800f081f （一个具体的 Windows 更新错误代码）

请思考一下：在这个场景下，如果我们只用 Dense 向量（没有 Sparse），可能会检索出什么样的"错误"结果？而 Sparse 向量又是如何修正这个问题的？

🕵️‍♂️ 为什么 Dense 会在这个场景下"脸盲"？

在 Dense 向量的世界里（那个 1024 维的浓雾中）：

Error 0x800f081f
Error 0xc1900101

这两个词组在语义上几乎是一模一样的。它们的意思都是："Windows 更新失败了，用户很生气"。😤

所以，Dense 模型会把这两句话映射到距离非常近的位置。当你搜 0x800f081f 时，Dense 可能会给你返回一大堆关于 0xc1900101 的修复指南，因为它觉得"意思差不多嘛"。这就是所谓的检索幻觉。

🎯 为什么 Sparse 能一击必中？

而在 Sparse 向量的世界里（那个 25 万维的星空）：

0x800f081f 是第 102,456 号星星。
0xc1900101 是第 205,888 号星星。

它们是完全不同的两个维度（Dimension）。Sparse 向量看到你的查询里有 0x800f081f，它就会像激光制导一样，只去找点亮了这颗特定星星的文档。如果没有这串代码，权重就是 0，直接过滤掉。

1.4 Multi-vector

1.4.1 Multi-Vector (多向量检索 / ColBERT) 🤝

核心理念：拒绝压缩。
- 不同于 Dense 将整句压缩为 1 个向量，Multi-Vector 保留输入序列中每一个 Token 的向量。
- 比喻：就像"全员面试"，Query 中的每个词都要去和 Document 中的每个词"见面"交互。
交互机制：迟交互 (Late Interaction) 🐢
- 步骤：
  1. 计算 Query 中每个 Token 向量与 Document 中所有 Token 向量的相似度。
  2. MaxSim：为 Query 的每个词找到文档中"最匹配"的那个词。
  3. 求和：将这些最高分相加得到最终分数。
- 优势：能捕捉极细微的语义（如否定词、介词），精度极高。

💡 关键问答推导 (Q&A Summary)

问题 1：关于存储与效率的数学账 🧮

场景：假设向量维度 d=1024d=1024d=1024，文档长度 128 Token。
对比：
- Dense: 存 1 个向量。
- Multi-Vector: 需存 128 个向量。
推论：存储空间需求暴增 128 倍。对于 1 亿篇文档的索引，Dense 仅需约 200GB (内存可放)，而 Multi-Vector 需要约 25TB (必须分布式存储)。

问题 2：面对 1 亿篇文档的检索挑战 📉

挑战：如果直接用 Multi-Vector 在 1 亿篇文档中搜索，计算量巨大（每次查询需进行 N×MN \times MN×M 次交互），会导致 CPU/GPU 算力崩溃，延迟极高。
结论： Multi-Vector 不适合直接用于海量数据的"初筛"。
最终解决方案：漏斗模型 (Retrieval-Rerank Pipeline) ⚡
策略：扬长避短。
1. 第一步 (海选/Retrieve)：用 Dense 或 Sparse 快速从 1 亿篇中筛选出 1000 篇（快但粗）。
2. 第二步 (精筛/Rerank)：用 Multi-Vector 对这 1000 篇进行精细交互，选出 Top 10（准但贵）。