【算法基础篇】（三十八）数论之最大公约数与最小公倍数 —— 从原理到实战

前言

在算法竞赛的数学模块中，最大公约数（gcd）和最小公倍数（lcm）是当之无愧的基础核心。无论是后续的数论推导、动态规划优化，还是实际工程中的数据处理，这两个概念都扮演着不可或缺的角色。很多新手觉得数论晦涩难懂，但其实只要抓住本质、理清逻辑，gcd 和 lcm 的学习完全可以轻松上手。本文将从定义出发，深入原理，结合实战例题，用生动易懂的语言带你彻底掌握这一知识点，可直接用于竞赛刷题！下面就让我们正式开始吧！

一、从概念到本质：什么是约数、倍数、gcd 和 lcm？

在正式讲解算法之前，我们先明确几个最基础的概念，打好理论地基。毕竟再复杂的算法，也是基于简单概念的延伸。

1.1 约数和倍数的定义

如果一个整数a除以另一个整数b（b≠0）的余数为 0，我们就说a是b的倍数，b是a的约数（也叫因数），记作b | a。比如 12 除以 3 余数为 0，那么 3 是 12 的约数，12 是 3 的倍数，写成3 | 12。

这个概念看似简单，但有两个关键点需要注意：

约数和倍数是相互依存的，不能单独说 "5 是约数" 或 "10 是倍数"，必须明确谁是谁的约数、谁是谁的倍数；

约数具有对称性，若b是a的约数，则a/b也一定是a的约数（前提是a能被b整除），这一点在后续算法优化中会起到重要作用。

1.2 最大公约数（gcd）：所有公约数中的 "老大"

我们先看公约数的定义：如果一个整数d同时是整数a₁, a₂, ..., aₙ中每一个数的约数，那么d就叫做这n个数的公约数。而最大公约数，就是所有公约数中最大的那个数，记作gcd(a₁, a₂, ..., aₙ)。

举个例子：求 12、34、56 的最大公约数。首先列出它们的约数：

12 的约数：1、2、3、4、6、12；

34 的约数：1、2、17、34；

56 的约数：1、2、4、7、8、14、28、56；它们的公约数是 1 和 2，其中最大的是 2，所以gcd(12,34,56)=2，这也是我们后面实战例题的一个答案。

1.3 最小公倍数（lcm）：所有公倍数中的 "最小鲜肉"

公倍数的定义与公约数对应：如果一个整数m同时是整数a₁, a₂, ..., aₙ中每一个数的倍数，那么m就叫做这n个数的公倍数。最小公倍数则是所有正的公倍数中最小的那个数，记作lcm(a₁, a₂, ..., aₙ)。

比如求 4 和 6 的最小公倍数：

4 的倍数：4、8、12、16、20、24...；

6 的倍数：6、12、18、24、30...；它们的公倍数有 12、24 等，其中最小的是 12，所以lcm(4,6)=12。

1.4 gcd 和 lcm 的核心关系：相辅相成

这里有一个至关重要的性质，也是我们计算 lcm 的关键：对于任意两个正整数 a 和 b，它们的最大公约数与最小公倍数的乘积等于这两个数的乘积 ，即：gcd(a, b) × lcm(a, b) = a × b

这个性质的证明其实很简单（后续会简要提及），但它的实用价值极大。因为计算 lcm 直接求解比较麻烦，但如果我们能先求出 gcd，就可以通过公式lcm(a,b) = a×b / gcd(a,b)快速得到 lcm。需要注意的是，为了避免整数溢出（尤其是在 a 和 b 较大的情况下），我们通常会调整计算顺序，写成lcm(a,b) = a / gcd(a,b) × b，因为 gcd (a,b) 一定能整除 a，先做除法可以保证中间结果不会超出整数范围。

二、欧几里得算法：求 gcd 的 "王牌算法"

知道了 gcd 的定义，接下来就是核心问题：如何高效计算两个数的最大公约数？暴力枚举虽然可行，但效率太低，对于大数完全不适用。而欧几里得算法（又称辗转相除法），凭借其对数级的时间复杂度，成为了求解 gcd 的首选算法。

2.1 欧几里得算法的原理

欧几里得算法的核心思想可以用一句话概括：对于两个正整数 a 和 b（a > b），gcd (a, b) = gcd (b, a mod b) ，其中a mod b表示 a 除以 b 的余数（取值范围是 0 ≤ 余数 < b）。

这个结论看起来有点抽象，我们用一个例子验证一下：求 gcd (12, 8)。

根据算法，gcd (12,8) = gcd (8, 12 mod 8) = gcd (8,4)；

再应用一次算法：gcd (8,4) = gcd (4, 8 mod 4) = gcd (4,0)；

当余数为 0 时，此时的除数就是原来两个数的最大公约数，即 gcd (4,0)=4；

最终结果 gcd (12,8)=4，和我们手动计算的一致。

再举一个例子：gcd (34,12)。

gcd(34,12) = gcd(12, 34 mod 12) = gcd(12,10)；

gcd(12,10) = gcd(10, 12 mod 10) = gcd(10,2)；

gcd(10,2) = gcd(2, 10 mod 2) = gcd(2,0)；

结果为 2，正确。

2.2 为什么这个算法是正确的？

很多同学可能会疑惑，为什么 gcd (a,b) 会等于 gcd (b,a mod b)？我们来做一个简单的证明，理解其本质。

首先明确符号定义：设a = k×b + r，其中k = a//b（整数除法），r = a mod b（余数），所以0 ≤ r < b。我们需要证明的是：gcd (a,b) = gcd (b,r)。

证明过程分为两步：

证明 gcd (a,b) ≤ gcd (b,r)： 设 d 是 a 和 b 的任意一个公约数，即 d | a 且 d | b。根据整除的性质，d 可以整除 a 和 b 的任意线性组合。而 r = a - k×b，所以 d | (a - k×b)，即 d | r。这说明 d 也是 b 和 r 的公约数，因此 gcd (a,b) 作为 a 和 b 的最大公约数，必然小于等于 b 和 r 的最大公约数，即gcd (a,b) ≤ gcd (b,r)。

证明 gcd (b,r) ≤ gcd (a,b)： 设 d 是 b 和 r 的任意一个公约数，即 d | b 且 d | r。同样根据线性组合的性质，a = k×b + r，所以 d | (k×b + r)，即 d | a。这说明 d 也是 a 和 b 的公约数，因此 gcd (b,r) 必然小于等于 a 和 b 的最大公约数，即 gcd (b,r) ≤ gcd (a,b)。

结合以上两步，可得 gcd (a,b) = gcd (b,r)，即 gcd (a,b) = gcd (b,a mod b)，欧几里得算法的正确性得证。

2.3 欧几里得算法的 C++ 实现

根据上述原理，我们可以用递归或迭代的方式实现欧几里得算法。递归实现简洁直观，迭代实现则可以避免栈溢出（但对于竞赛中的数据范围，递归深度完全足够）。

递归实现

cpp 复制代码

#include <iostream>
using namespace std;

// 递归实现欧几里得算法
long long gcd(long long a, long long b) {
    // 递归终止条件：当b为0时，a就是最大公约数
    if (b == 0) return a;
    // 递归调用：gcd(a,b) = gcd(b, a mod b)
    return gcd(b, a % b);
}

int main() {
    long long a, b;
    cin >> a >> b;
    // 处理a < b的情况，此时gcd(a,b) = gcd(b,a)，递归会自动处理
    cout << "gcd(" << a << ", " << b << ") = " << gcd(a, b) << endl;
    return 0;
}

迭代实现

cpp 复制代码

#include <iostream>
using namespace std;

// 迭代实现欧几里得算法
long long gcd_iter(long long a, long long b) {
    // 当b不为0时，持续更新a和b
    while (b != 0) {
        long long temp = b;
        b = a % b;
        a = temp;
    }
    return a;
}

int main() {
    long long a, b;
    cin >> a >> b;
    cout << "gcd(" << a << ", " << b << ") = " << gcd_iter(a, b) << endl;
    return 0;
}

两种实现的核心逻辑一致，只是代码形式不同。递归实现更简洁，迭代实现则在理论上更节省栈空间，但在实际竞赛中，递归实现已经完全够用。

2.4 时间复杂度分析

欧几里得算法的时间复杂度是**O(log n)**，其中n是两个数中较大的那个。为什么是对数级别的呢？

我们可以分两种情况讨论：

当a < b时，gcd (a,b) = gcd (b,a)，相当于交换了两个数的位置，这一步是常数时间；

当a > b时，a mod b的结果一定小于b，而且根据数学推导，a mod b ≤ a/2（可以用反证法证明：假设a mod b > a/2，则a = k×b + r，其中r > a/2，由于r < b，所以b > r > a/2，那么k只能是 0，此时r = a，与r > a/2矛盾，因此假设不成立）。

这意味着每两次迭代，较大的数至少会减少一半，因此迭代次数最多是log₂n次，时间复杂度为O(log n)，对于10¹⁸级别的大数，也只需几十次迭代就能得出结果，效率极高。

三、最小公倍数的计算：基于 gcd 的推导

有了计算 gcd 的方法，结合我们之前提到的核心性质gcd(a,b) × lcm(a,b) = a × b，就可以轻松计算 lcm 了。

3.1 lcm 的 C++ 实现

cpp 复制代码

#include <iostream>
using namespace std;

long long gcd(long long a, long long b) {
    return b == 0 ? a : gcd(b, a % b);
}

// 计算最小公倍数
long long lcm(long long a, long long b) {
    if (a == 0 || b == 0) return 0; // 避免0的情况
    // 先除后乘，防止溢出
    return a / gcd(a, b) * b;
}

int main() {
    long long a, b;
    cin >> a >> b;
    cout << "lcm(" << a << ", " << b << ") = " << lcm(a, b) << endl;
    return 0;
}

这里有一个非常重要的细节：必须先做除法再做乘法 。如果写成a * b / gcd(a,b)，当 a 和 b 都是大数（比如10⁹级别）时，a*b的结果会达到10¹⁸，超过了 32 位整数的范围（最大是2³¹-1≈2×10⁹），即使是 64 位整数（最大是9×10¹⁸），也可能在更大的数面前溢出。而先做a / gcd(a,b)，由于 gcd (a,b) 是 a 的约数，结果一定是整数，再乘以 b 就不会出现中间结果溢出的问题。

3.2 多个数的 gcd 和 lcm 计算

前面我们讨论的都是两个数的情况，但实际问题中经常会遇到多个数的 gcd 和 lcm 计算。比如求三个数 x、y、z 的 gcd，该怎么做呢？

其实很简单，多个数的 gcd 和 lcm 可以通过迭代计算两个数的结果来得到：

多个数的 gcd：gcd(a₁,a₂,a₃,...,aₙ) = gcd(gcd(a₁,a₂),a₃),...,aₙ)；

多个数的 lcm：lcm(a₁,a₂,a₃,...,aₙ) = lcm(lcm(a₁,a₂),a₃),...,aₙ)。

举个例子，求 gcd (12,34,56)：

先计算 gcd (12,34)=2；

再计算 gcd (2,56)=2；

最终结果就是 2，和之前的例子一致。

再比如求 lcm (4,6,8)：

先计算 lcm (4,6)=12；

再计算 lcm (12,8)=24；

最终结果是 24。

下面给出多个数的 gcd 和 lcm 的 C++ 实现：

多个数的 gcd

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

long long gcd(long long a, long long b) {
    return b == 0 ? a : gcd(b, a % b);
}

// 计算多个数的gcd
long long gcd_multiple(const vector<long long>& nums) {
    long long result = nums[0];
    for (size_t i = 1; i < nums.size(); ++i) {
        result = gcd(result, nums[i]);
        if (result == 1) break; // 1和任何数的gcd都是1，无需继续计算
    }
    return result;
}

int main() {
    vector<long long> nums = {12, 34, 56};
    cout << "gcd of ";
    for (size_t i = 0; i < nums.size(); ++i) {
        if (i > 0) cout << ", ";
        cout << nums[i];
    }
    cout << " is " << gcd_multiple(nums) << endl;
    return 0;
}

多个数的 lcm

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

long long gcd(long long a, long long b) {
    return b == 0 ? a : gcd(b, a % b);
}

long long lcm(long long a, long long b) {
    return a == 0 || b == 0 ? 0 : a / gcd(a, b) * b;
}

// 计算多个数的lcm
long long lcm_multiple(const vector<long long>& nums) {
    long long result = nums[0];
    for (size_t i = 1; i < nums.size(); ++i) {
        result = lcm(result, nums[i]);
        if (result == 0) break; // 有一个数为0，lcm为0
    }
    return result;
}

int main() {
    vector<long long> nums = {4, 6, 8};
    cout << "lcm of ";
    for (size_t i = 0; i < nums.size(); ++i) {
        if (i > 0) cout << ", ";
        cout << nums[i];
    }
    cout << " is " << lcm_multiple(nums) << endl;
    return 0;
}

这里有一个优化点：计算多个数的 gcd 时，如果中间结果出现 1，那么最终结果一定是 1，因为 1 和任何数的 gcd 都是 1，此时可以直接跳出循环，节省计算时间。

四、实战例题：从基础到进阶，巩固知识点

理论学得再好，也需要通过实战来巩固。下面我们选取两道经典例题，分别对应基础应用和进阶技巧，帮助大家更好地掌握 gcd 和 lcm 的用法。

例题 1：洛谷 B3736 最大公约数（基础题）

题目链接：https://www.luogu.com.cn/problem/B3736

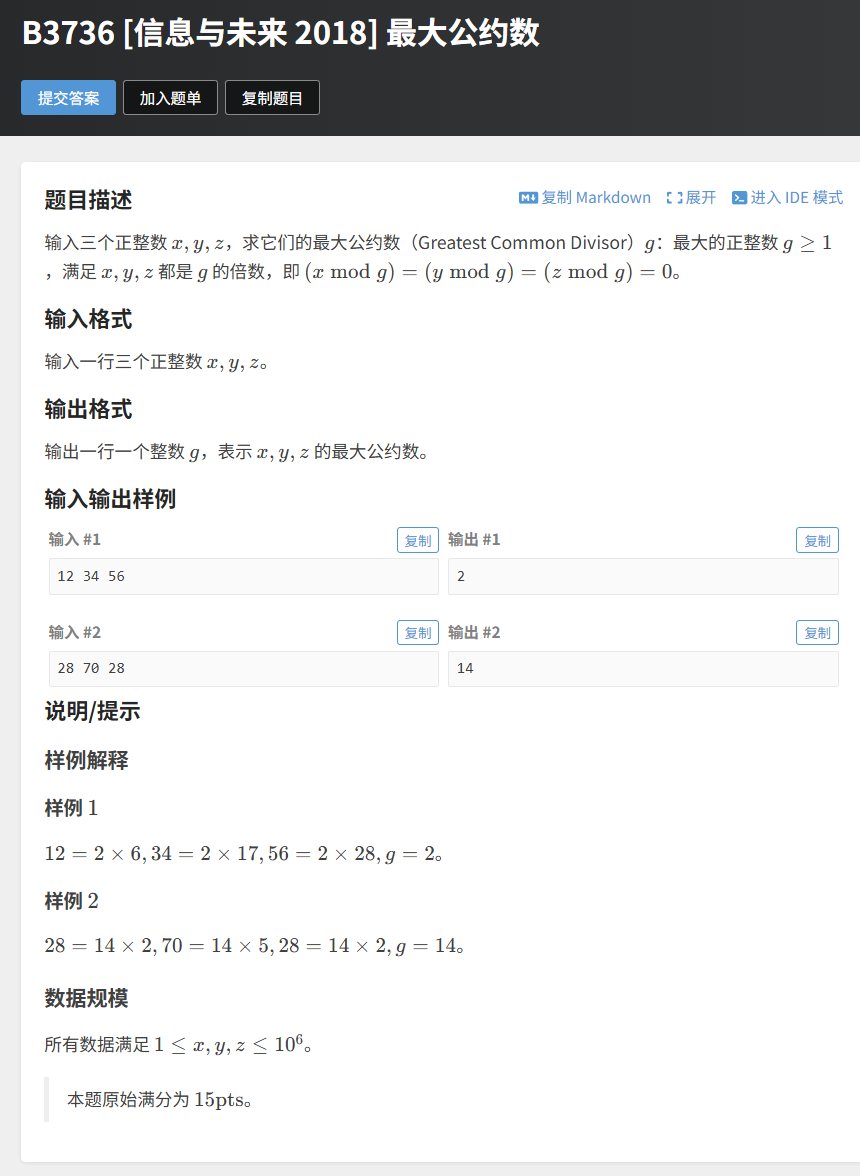
题目描述

输入三个正整数 x、y、z，求它们的最大公约数。

输入描述

输入一行三个正整数 x、y、z。

输出描述

输出一行一个整数 g，表示 x、y、z 的最大公约数。

示例输入

12 34 56

示例输出

解题思路

这道题是多个数 gcd 计算的直接应用，按照我们之前讲的迭代方法，先求前两个数的 gcd，再与第三个数求 gcd 即可。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;

// 递归实现gcd
int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

int main() {
    int x, y, z;
    cin >> x >> y >> z;
    // 先求x和y的gcd，再与z求gcd
    int result = gcd(gcd(x, y), z);
    cout << result << endl;
    return 0;
}

代码解释

首先定义 gcd 函数，用于计算两个数的最大公约数；

在 main 函数中读取三个输入值 x、y、z；

调用 gcd 函数两次，第一次计算 x 和 y 的 gcd，第二次将结果与 z 进行计算，得到三个数的 gcd；

输出结果，代码简洁明了，时间复杂度为 O (log max (x,y,z))，效率极高。

例题 2：牛客网小红的 gcd（进阶题）

题目链接：https://ac.nowcoder.com/acm/problem/275615

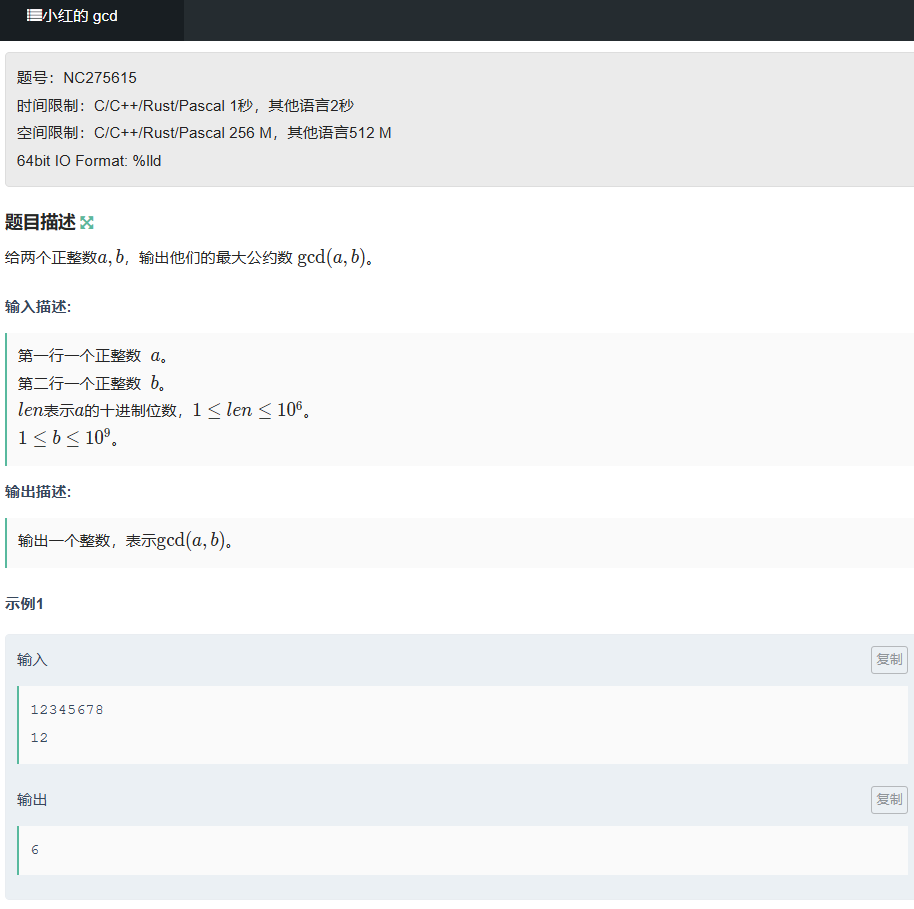
题目描述

给两个正整数 a、b，输出它们的最大公约数 gcd (a, b)。

输入描述

第一行一个正整数 a（十进制位数 len 满足 1 ≤ len ≤ 10⁶）；第二行一个正整数 b（1 ≤ b ≤ 10⁹）。

输出描述

输出一个整数，表示 gcd (a, b)。

示例输入

1234567812

示例输出

解题思路

这道题的难点在于 a 的位数非常大（最多 10⁶位），远远超过了 64 位整数的存储范围，无法直接用常规的整数类型存储，因此不能直接调用欧几里得算法。

这时候我们需要用到一个关键性质：gcd(a, b) = gcd(a mod b, b)。由于 a 的位数太大，我们可以先计算 a mod b 的值（记为 r），然后求 gcd (r, b)，结果就是原来的 gcd (a, b)。

那么问题就转化为：如何计算一个超大数（以字符串形式存储）对 b 的取模结果？这里可以用到秦九韶算法（也叫霍纳法则），将大数的取模过程分解为逐位计算，避免存储整个大数。

秦九韶算法的核心思想是：**对于一个大数a = dₙdₙ₋₁...d₁d₀（dₙ是最高位），其对 b 的取模可以表示为：**a mod b = (((...((dₙ × 10) + dₙ₋₁) × 10 + dₙ₋₂) × 10 + ...) × 10 + d₀) mod b

通过这种方式，我们可以逐位处理字符串，每次只保留当前的模运算结果，避免溢出，同时高效计算出 a mod b 的值。

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <string>
using namespace std;

// 计算两个数的gcd
int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

// 计算大数a（字符串形式）对b的取模结果
long long mod_big_number(const string& a, int b) {
    long long result = 0;
    for (char ch : a) {
        // 逐位处理，秦九韶算法
        result = (result * 10 + (ch - '0')) % b;
    }
    return result;
}

int main() {
    string a;
    int b;
    cin >> a >> b;
    // 计算a mod b
    long long r = mod_big_number(a, b);
    // 求gcd(r, b)
    int result = gcd(b, r);
    cout << result << endl;
    return 0;
}

代码解释

gcd 函数：与之前一致，用于计算两个整数的最大公约数；

mod_big_number 函数 ：接收字符串形式的大数 a 和整数 b，返回 a mod b 的结果。通过秦九韶算法逐位处理字符，每次更新 result 为**(result * 10 + 当前位数字) % b**，确保 result 始终在整数范围内，不会溢出；

main 函数：读取字符串 a 和整数 b，调用 mod_big_number 得到 a mod b 的值 r，再调用 gcd (b, r) 得到最终结果并输出。

时间复杂度分析

mod_big_number 函数的时间复杂度为O (len (a))，其中 len (a) 是大数 a 的位数（最多 10⁶）；

gcd 函数的时间复杂度为O (log b)（b 最多 10⁹，log₂b 约为 30）；

总体时间复杂度为 O (len (a))，对于 10⁶位的输入，完全可以在时间限制内完成。

这道题的关键在于灵活运用 gcd 的性质和秦九韶算法，解决了超大数无法存储的问题，是竞赛中常见的进阶考法。

五、常见误区与注意事项

在使用 gcd 和 lcm 的过程中，新手很容易出现一些错误，这里总结几个常见误区，帮助大家避坑：

5.1 忽视 0 的情况

0 和任何非零整数的 gcd 是该非零整数（因为 0 是任何非零整数的倍数，非零整数是 0 的约数）；

0 和 0 的 gcd 是未定义的（但实际编程中通常返回 0）；

计算 lcm 时，如果有一个数为 0，lcm 为 0（因为 0 是任何数的倍数）。

在编程时，建议先对输入进行判断，处理掉 0 的情况，避免出现逻辑错误。

5.2 整数溢出问题

计算 lcm 时，一定要先做除法再做乘法，即a / gcd(a,b) * b，而不是a*** b / gcd(a,b)**；

对于超大数（如例题 2），不能直接用整数类型存储，需要用字符串处理并结合取模运算。

5.3 递归深度问题

欧几里得算法的递归实现虽然简洁，但对于极特殊的情况（如两个数连续递减），递归深度可能会较大，导致栈溢出；

如果担心栈溢出，可以使用迭代实现，或者在 C++ 中通过调整栈大小来解决（但竞赛中通常不需要）。

5.4 多个数的 lcm 计算顺序

多个数的 lcm 计算顺序不影响结果，但建议按照从左到右的顺序迭代计算，避免中间结果过大；

计算多个数的 lcm 时，若中间结果出现 0，说明有一个输入数为 0，此时可以直接返回 0，无需继续计算。

总结

数论的学习就像搭积木，每一个知识点都是后续学习的基础。希望本文能够帮助你扎实掌握 gcd 和 lcm，为后续的数论学习打下坚实的基础。如果在学习过程中有任何问题，欢迎在评论区留言讨论！

【算法基础篇】（三十八）数论之最大公约数与最小公倍数 —— 从原理到实战

目录

前言

一、从概念到本质：什么是约数、倍数、gcd 和 lcm？

1.1 约数和倍数的定义

1.2 最大公约数（gcd）：所有公约数中的 "老大"

1.3 最小公倍数（lcm）：所有公倍数中的 "最小鲜肉"

1.4 gcd 和 lcm 的核心关系：相辅相成

二、欧几里得算法：求 gcd 的 "王牌算法"

2.1 欧几里得算法的原理

2.2 为什么这个算法是正确的？

2.3 欧几里得算法的 C++ 实现

递归实现

迭代实现

2.4 时间复杂度分析

三、最小公倍数的计算：基于 gcd 的推导

3.1 lcm 的 C++ 实现

3.2 多个数的 gcd 和 lcm 计算

多个数的 gcd

多个数的 lcm

四、实战例题：从基础到进阶，巩固知识点

例题 1：洛谷 B3736 最大公约数（基础题）

题目描述

输入描述

输出描述

示例输入

示例输出

解题思路

C++ 代码实现

代码解释

例题 2：牛客网 小红的 gcd（进阶题）

题目描述

输入描述

输出描述

示例输入

示例输出

解题思路

C++ 代码实现

代码解释

时间复杂度分析

五、常见误区与注意事项

5.1 忽视 0 的情况

5.2 整数溢出问题

5.3 递归深度问题

5.4 多个数的 lcm 计算顺序

总结

例题 2：牛客网小红的 gcd（进阶题）