leetcode 756. 金字塔转换矩阵中等

你正在把积木堆成金字塔。每个块都有一个颜色，用一个字母表示。每一行的块比它下面的行 少一个块 ，并且居中。

为了使金字塔美观，只有特定的 三角形图案 是允许的。一个三角形的图案由 两个块 和叠在上面的 单个块 组成。模式是以三个字母字符串的列表形式 allowed 给出的，其中模式的前两个字符分别表示左右底部块，第三个字符表示顶部块。

例如，"ABC" 表示一个三角形图案，其中一个 "C" 块堆叠在一个 'A' 块(左)和一个 'B' 块(右)之上。请注意，这与 "BAC" 不同，"B" 在左下角，"A" 在右下角。

你从作为单个字符串给出的底部的一排积木 bottom 开始，必须将其作为金字塔的底部。

在给定 bottom 和 allowed 的情况下，如果你能一直构建到金字塔顶部，使金字塔中的 每个三角形图案 都是在 allowed 中的，则返回 true ，否则返回 false 。

示例 1：

复制代码

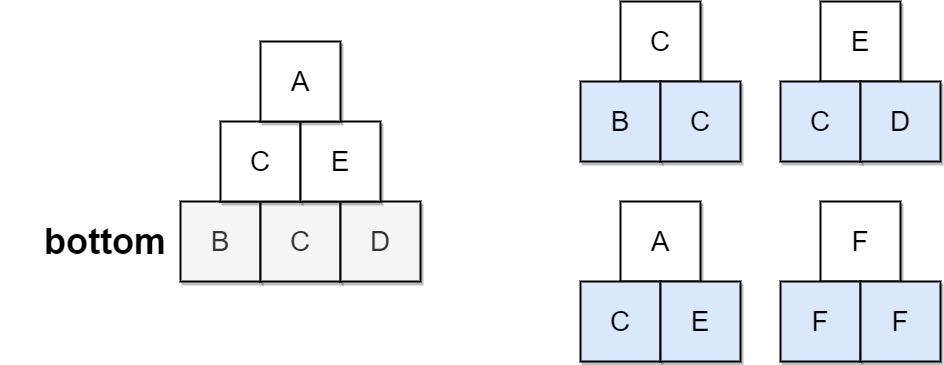
输入：bottom = "BCD", allowed = ["BCC","CDE","CEA","FFF"]
输出：true
解释：允许的三角形图案显示在右边。
从最底层(第 3 层)开始，我们可以在第 2 层构建“CE”，然后在第 1 层构建“E”。
金字塔中有三种三角形图案，分别是 “BCC”、“CDE” 和 “CEA”。都是允许的。

示例 2：

复制代码

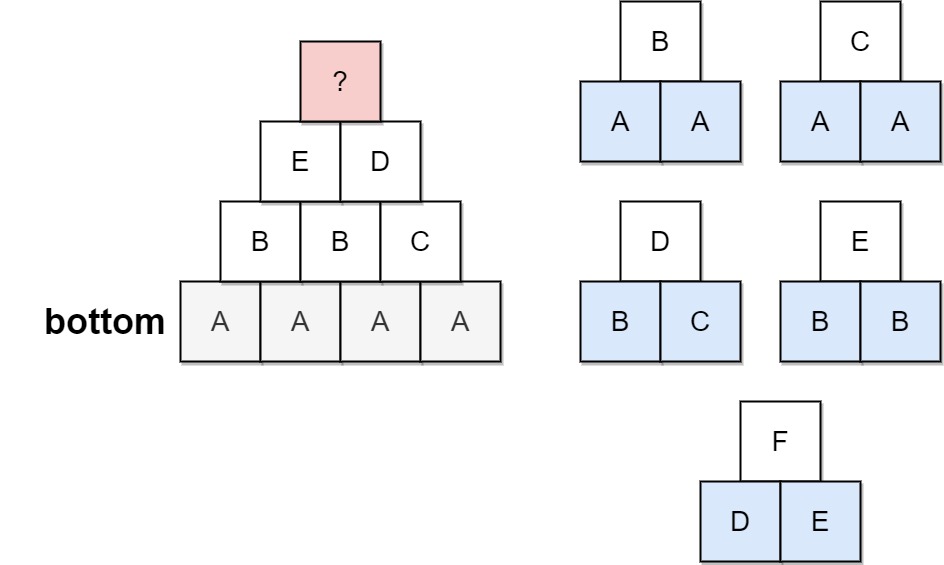
输入：bottom = "AAAA", allowed = ["AAB","AAC","BCD","BBE","DEF"]
输出：false
解释：允许的三角形图案显示在右边。
从最底层(即第 4 层)开始，创造第 3 层有多种方法，但如果尝试所有可能性，你便会在创造第 1 层前陷入困境。

提示：

2 <= bottom.length <= 6
0 <= allowed.length <= 216
allowed[i].length == 3
所有输入字符串中的字母来自集合 {'A', 'B', 'C', 'D', 'E', 'F'}。
allowed 中所有值都是 唯一的

分析：按照从下往上，从左向右的顺序，依次填三角形的每一个位置，对每个位置都进行 DFS，枚举所有可能填的字母。注意有部分底层的两个字母是不能填完整个三角形的，因此进行 DFS 的时候，可以先检查底层的两个字母是不是可以填完，如果不能填完，则直接返回 false。

cpp 复制代码

class Solution {
public:
    char pyramid[10][10],allow[10][10][10];
    bool ans=false;
    map<string,int>refuse;

    bool dfs(int x,int y,int level)
    {
        bool flag=false;

        for(int i=1;i<=6;++i)
        {
            int ind_x=pyramid[x+1][y]-'A'+1,ind_y=pyramid[x+1][y+1]-'A'+1;
            // 下一行的两个无法凑出三角形，记录这个不能凑，并返回false
            if(allow[ind_x][ind_y][0]==0)
            {
                string temp="";temp+=pyramid[x+1][y];temp+=pyramid[x+1][y+1];refuse[temp]=1;
                // printf("level=%d x=%d y=%d ",level,x,y);
                cout<<temp<<endl;
                return false;
            }
            // 下一行的两个可以凑，进行dfs
            if(allow[ind_x][ind_y][i])
            {
                pyramid[x][y]='A'+i-1;
                if(y>=2)
                {
                    string temp="";
                    temp+=pyramid[x][y-1];
                    temp+=pyramid[x][y];
                    if(refuse[temp])return false;
                }
                // 这一行已经填完了
                if(y==level)
                {
                    // 填完了第一行
                    if(level==1)return true;
                    // 填完的不是第一行，继续填上一行
                    else flag=dfs(x-1,1,level-1);
                }
                // 继续填下一个
                else flag=dfs(x,y+1,level);
                if(flag==true)return true;
            }
        }
        return flag;
    }

    bool pyramidTransition(string bottom, vector<string>& allowed) {
        bool flag=true;
        int n=allowed.size(),len=bottom.size();
        for(int i=0;i<n;++i)
        {
            int x=allowed[i][0]-'A'+1,y=allowed[i][1]-'A'+1,z=allowed[i][2]-'A'+1;
            allow[x][y][z]=1,allow[x][y][0]++;
        }
        for(int i=0;i<len;++i)
            pyramid[len][i+1]=bottom[i];

        flag=dfs(len-1,1,len-1);
        return flag;
    }
};

leetcode 756. 金字塔转换矩阵 中等

leetcode 756. 金字塔转换矩阵中等