c++图论——生成树之Kruskal&Prim算法

Bruce_kaizy2025-12-30 16:14

目录

一，最小生成树简介

[最小生成树的性质：1，mst的边权和是所有生成树中最小的 2，mst的最大边权是所有生成树中最小的](#最小生成树的性质：1，mst的边权和是所有生成树中最小的 2，mst的最大边权是所有生成树中最小的)

二，Kruskal算法

为什么要排序？

怎么理解剔除边和保留边？

例题训练：

蓝桥杯官网------旅行销售员

问题描述

输入格式

输出格式

样例输入

样例输入

样例输出

评测数据规模

代码详解（kruskal）

三，Prim算法

例题训练：就是上面那道

代码详解：

注：本文所有题目均来自蓝桥杯官网公开真题，仅做算法学习，代码皆由本人做出来并附上解析！

一，最小生成树简介

最小生成树（mst,Minimum Spanning Tree）是指，对于一个连通图，剔除其中一部分边，而保留一部分边，使得剩下的部分构成一棵树，并且这棵树的所有边的权值之和最小(保持树的特性n个点，n-1条边)。例如在下图中，绿色部分的边组成的树就是一棵最小生成树。最小生成树所处理的图的边权一般是不相等的，否则意义不大。常见的求最小生成树的算法有 Kruskal 算法（O (mlogm)）和 Prim 算法（O (mlogn)）。

注意：最小生成树只针对无向图！！！不能用有向图！！！

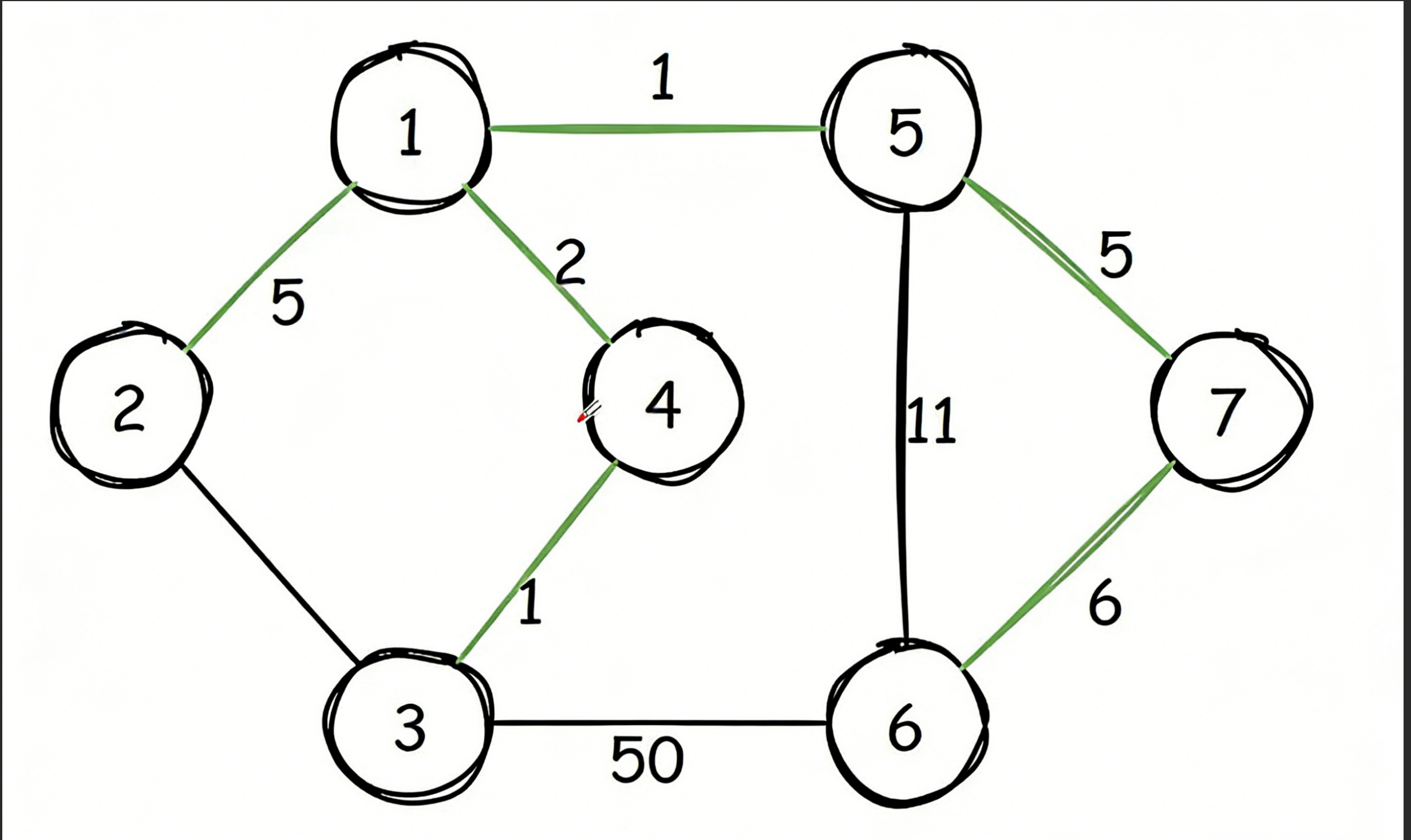
最小生成树的性质：1，mst的边权和是所有生成树中最小的 2，mst的最大边权是所有生成树中最小的

二，Kruskal算法

Kruskal 算法基于贪心的想法，步骤十分简单。

  1. 将所有边按照边权排序。

  2. 从小到大遍历所有边 (u, v)，如果 (u, v) 已经连通就跳过，否则就选中 (u, v)，将它俩相连（要用到并查集）。

代码如下：

cpp 复制代码 
​
​
//KRUSKAL
// 代码：求解最小生成树中最大边权值
struct edge
{
	int x, y, c;
	bool operator<(const edge& u)const
	{
		return c < u.c;// 按照边的权值从小到大排序
	}
};

int pre[N];
int root(int x)//并查集
{
	return pre[x] = (pre[x] == x ? x : root(pre[x]));
}

void solve()
{
	int n, m; cin >> n >> m;
	vector<edge>es;
	for (int i = 1; i <= m; i++)
	{
		int x, y, c; cin >> x >> y >> c;
		es.push_back({ x,y,c });// 将边加入向量容器
	}
	sort(es.begin(), es.end());
	for (int i = 1; i <= n; i++)
	{
		pre[i] = i;
	}
	int ans = 0;

	for (const auto& [x, y, c] : es)
	{
		if (root(x) == root(y))continue;
		/*这句话的意思是：「如果 x 和 y 已经在同一个连通集合中（即两点已经通过之前的边连接起来了），就跳过当前这条边」
作用：避免添加会形成回路的边（最小生成树不能有回路）*/
		//因为连接一个联通块的两点就会形成环，而树不能有环
		ans = max(ans, c);// 更新当前最小生成树中最大边的权值
		pre[root(x)] = root(y);
        //刚开始所有点都不连通，先联通第一条边，在以此类推
		/*意思是：「把 x 和 y 所在的两个连通集合合并成一个，让它们从此连通」
作用：记录新的连通关系，为后续判断做准备*/
	}
	cout << ans << '\n';
}
/*pre[root(x)] = root(y);能不能写成pre[root(y)] = root(x)?
是可以的。pre[root(x)] = root(y); 和 pre[root(y)] = root(x); 
这两种两种写法在功能上是等价的，都是将两个不同的集合合并，只是合并的方向不同：
无论哪种写法，都必须先通过 root() 函数找到各自的根节点，再进行合并，而不能直接写 pre[x] = y; 或 pre[y] = x;。*/

​

​

为什么要排序？

排序是为了实现 Kruskal 算法的"贪心策略"，最终确保构建出的是"最小生成树（MST）"，而不是任意生成树，具体拆解如下：

明确核心目的：实现贪心策略，保证得到"最小"生成树

Kruskal 算法的核心是贪心算法思想，而"对边按权值从小到大排序"是实现这一贪心策略的前提。

贪心策略的核心逻辑：为了构建总权值最小的生成树，我们要尽可能优先选择权值小的边，同时避免形成回路。

1.如果不排序，随机选择边来构建生成树，最终得到的只是一棵普通生成树，其总权值很可能不是最小的，无法满足「最小生成树」的求解要求；

2.排序后，我们能确保遍历边的顺序是「从权值最小到最大」，每一步都做局部最优选择（选当前最小的有效边），最终累积得到全局最优结果（总权值最小的生成树）。

注意！最小生成树的最大边 ≠ 原来图的最大边（因为已经剔除了一部分！）

怎么理解剔除边和保留边？

明确前提：代码中的边都是原始输入的边，没有新增

  1. 代码中的es向量存储的是题目输入的所有原始边 （通过cin读取m条边并push_back存入），后续所有操作都基于这个原始边集，没有创建任何一条新的、不存在于输入中的边；
  2. 我们感觉上的 "新增边"，本质是将原始边集中的有效边 "标记为保留"（纳入最小生成树的边集合），而不是创建了新边。
  3. 筛选逻辑（核心是continue） ：
    • 遍历排序后的每条原始边，先判断x和y是否已连通；
    • 若已连通（root(x) == root(y)），说明这条边如果加入，会形成环（违反生成树的无环要求），因此跳过这条边（本质就是剔除它，不纳入生成树）；
    • 若未连通，说明这条边是有效边（加入后不会形成环，且能扩大连通范围），因此保留这条边（通过pre[root(x)] = root(y)合并连通集，标记为生成树的组成部分）；

代码中的[x, y, c]是一条x------y的已经存在的无向边，但是这一条边的两个点x，y有两种状态，一个是连通，一个是不连通。

例题训练：

蓝桥杯官网------旅行销售员

问题描述

蓝桥公司招聘了一个推销员。他大部分时间都在不同的城市之间旅行。他决定买一辆新车来帮助他的工作，但他必须决定新车油箱的容量。假设这辆新车每公里耗油一升。

每个城市至少有一个加油站，推销员可以在那里给油箱加油，但城市之间的道路上没有加油站。给出城市及其之间道路的描述，找出所需油箱的最小容量，以便推销员能够至少以一种方式在任何一对城市之间旅行。

输入格式

输入的第一行包含表示测试用例数的 T。

每个测试用例的第一行包含两个整数: N 和 M ，其中 N 为城市数量，M 为道路数量。

以下 M 行都包含三个整数: X,Y,C，其中 C 是城市 X 和城市 Y 之间的长度，单位为公里。道路可以双向使用。

题目保证每对城市之间最多有一条道路相连，并且可以使用给定的道路在任意一对城市之间旅行。

输出格式

对于每个测试用例，打印一行整数表示油箱所需的最小容量。

样例输入

样例输入

复制代码 
2
6 7
1 2 3
2 3 3
3 1 5
3 4 4
4 5 4
4 6 3
6 5 5
3 3
1 2 1
2 3 2
3 1 3

样例输出

复制代码 
4
2

评测数据规模

对于 100% 的评测数据，1 ≤ T ≤ 5, 3 ≤ N ≤ 100000, N − 1 ≤ M ≤ 100000, 1 ≤ X,Y ≤ N, X ≠ Y, 1 ≤ C ≤ 100000。

代码详解（kruskal）

cpp 复制代码 
//本体本质：求最小生成树的最大边权------kruskal
#include <iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N=1e5+9;
int n,m,pre[N];

struct Node
{
  int u,v,w;
  bool operator<(const Node &a)const
  {
    return w<a.w;
  }
};

int root(int x)
{
  return pre[x]==x?x:root(pre[x]);
}

//vector<Node>es;有多组数据，不能是全局变量！！！
//若是全局变量，要清空：.clear()

void solve()
{
  cin>>n>>m;
  vector<Node>es;
  int ans=0;
  for(int i=1;i<=m;i++)
  {
    int x,y,c;cin>>x>>y>>c;
    es.push_back({x,y,c});
  }
  //排序：
  sort(es.begin(),es.end());
  //初始化并查集
  for(int i=1;i<=n;i++) pre[i]=i;
  //开始合并：
  for(const auto &[u,v,w]:es)
  {
    if(root(u)==root(v)) continue;
    ans=max(ans,w);
    pre[root(u)]=root(v);
  }
  cout<<ans<<'\n';
}

int main()
{
  ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
  int T;cin>>T;
  while(T--)
  {
    solve();
  }
  return 0;
}

三，Prim算法

Prim 算法采用集合的思想，维护一个mst集合，里面存储已经在最小生成树中的点。

  1. 从起点（一般为 1 号点）出发，每次找出不在 mst 中且 d [] 最小的点 x ，d[x]就是选中的那条边的边权。
  2. 将点 x 加入到 mst 中，并更新其所有出点 y，更新d[y] = min(d[y], w);（w为 x->y 的距离）。
  3. 如果d[y]变小了，就加入到优先队列中作为可能的拓展点。

这个mst集合我们用bool数组或bitset来实现即可。

Prim 算法和 Dijkstra 算法思想类似，写法也类似，只有d数组的区别：

1.Dijkstra 算法中d[x]表示 x 到源点的最短距离。

2.Prim 算法中d[x]表示 x 到集合 mst 中任意一点的最短距离。

代码：

cpp 复制代码 
// prim代码：
struct edge
{
	ll x, c;
	/*ll x：ll通常是long long的 typedef（长整型），这里表示顶点编号。
ll c：表示权值（可以是边的权重，或顶点到生成树(mst集合)的当前最小权重）*/
	bool operator<(const edge& u)const
	{
		return c == u.c ? x > u.x:c > u.c;
	}
};
/*作用：C++ 优先队列（priority_queue）默认是 "大顶堆"（最大元素在队顶），
通过这样的重载，会让优先队列变成 "小顶堆"（权值c小的元素优先出队），符合 Prim 算法 "每次选最小权值边" 的贪心策略。*/
vector<edge>g[N];
ll d[N];
int n, m;
int prim()
{
	priority_queue<edge> pq;  // 优先队列（小顶堆），用于选最小权值的边
	bitset<N> vis;            // 标记顶点是否已加入生成树
	d[1] = 0;                 // 起点（顶点1）到生成树的初始权值为0
	pq.push({ 1, d[1] });       // 将起点加入优先队列
	ll res = 0;               // 存储结果：生成树中最大的边权

	while (pq.size())         // 当队列不为空时循环
	{
		int x = pq.top().x;   // 取出队顶元素的顶点x（当前权值最小的顶点）
		pq.pop();             // 弹出队顶元素

		if (vis[x]) continue; // 若x已加入生成树，跳过
		vis[x] = true;        // 标记x为已加入生成树
		res = max(res, d[x]); // 更新结果：取当前生成树中最大的边权

		// 遍历x的所有邻边
		for (const auto& [y, w] : g[x])
		{
			if (vis[y]) continue; // 若y已加入生成树，跳过
			// 若y到生成树的当前最小权值大于x到y的边权w，则更新
			d[y] = min(d[y], w);
			// 将更新后的y和其最小权值加入优先队列
			pq.push({ y, d[y] });
		}
	}
	return res;  // 返回生成树中最大的边权
}

例题训练：就是上面那道

代码详解：

cpp 复制代码 
//本体本质：求最小生成树的最大边权------prim
#include <iostream>
#include<vector>
#include<algorithm>
#include<bitset>
#include<queue>
using namespace std;
using ll=long long;
const ll inf=2e18;
const int N=1e5+9;
ll n,m,d[N];
//由于题目中说明了城市都是可以加油的，所以不需要考虑这个人走任意两个城市经过了多少边
//只需要考虑他走的两个相连城市的最大长度（即边权）
//要使得他走的两个相连城市的最大边权最小，就要考虑最小生成树的最大边权！

struct Node
{
  ll x,w;
  bool operator<(const Node &a)const//已经指定了结构体类型，不需要auto
  {
    return w>a.w;
  }
};

vector<Node>g[N];

ll prim()
{
  ll res=0;//栈空间要初始化为0！！！
  priority_queue<Node>pq;
  bitset<N>vis;
  //顶点入队
  pq.push({1,d[1]=0});
  while(pq.size())
  {
    ll x=pq.top().x;pq.pop();
    if(vis[x]==true) continue;
    vis[x]=true;
    res=max(res,d[x]);
    for(const auto &[y,dw]:g[x])
    {
      if(dw<d[y]) d[y]=dw;//是联通块，和d[x]无关！
      pq.push({y,d[y]});
    }
  }
  return res;
}

void solve()
{
  //g[N].clear();err
  cin>>n>>m;
  //初始化d
  for(int i=1;i<=n;i++)
  {
    g[i].clear();
    d[i]=inf;
  }
  for(int i=1;i<=m;i++)
  {
    int x,y,c;cin>>x>>y>>c;
    g[x].push_back({y,c});
    g[y].push_back({x,c});
  }
  cout<<prim()<<'\n';
}

int main()
{
  ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
  int T;cin>>T;
  while(T--)
  {
    solve();
  }
  return 0;
}

我想要你的关注可以吗？？？

相关推荐
LYFlied2 小时前
【每日算法】LeetCode 5. 最长回文子串(动态规划)
数据结构·算法·leetcode·职场和发展·动态规划
老赵聊算法、大模型备案3 小时前
《人工智能拟人化互动服务管理暂行办法（征求意见稿）》深度解读：AI“拟人”时代迎来首个专项监管框架
人工智能·算法·安全·aigc
雪花desu3 小时前
【Hot100-Java中等】/LeetCode 128. 最长连续序列：如何打破排序思维，实现 O(N) 复杂度？
数据结构·算法·排序算法
松涛和鸣3 小时前
41、Linux 网络编程并发模型总结（select / epoll / fork / pthread）
linux·服务器·网络·网络协议·tcp/ip·算法
鹿角片ljp3 小时前
力扣26.有序数组去重：HashSet vs 双指针法
java·算法
雾岛听蓝3 小时前
C++：模拟实现string类
开发语言·c++
XFF不秃头3 小时前
力扣刷题笔记-合并区间
c++·笔记·算法·leetcode
编程之路，妙趣横生3 小时前
STL(七) unordered_set 与 unordered_map 基本用法 + 模拟实现
c++
寂柒3 小时前
c++--
c++
热门推荐
01GitHub 镜像站点02从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击03Linux下V2Ray安装配置指南04Claude Code Skills 实用使用手册05电脑检测软件—图吧工具箱06jdk21下载、安装（Windows、Linux、macOS）07UV安装并设置国内源08【踩坑笔记】50系显卡适配的 PyTorch 安装092025-04-03 Latex学习1——本地配置Latex + VScode环境10SQLmap 完整使用指南：环境搭建 + 命令详解 + 实操案例