一、核心思想
目标:在喷墨打印纳米银导线的复杂工艺中,寻找一组或多组最优的工艺参数组合,以同时优化多个性能指标(如导电性、分辨率、机械柔韧性、成本、烧结效率等)。
挑战:
多目标冲突:例如,提高导电性(如增加层数、提高温度)可能降低分辨率或增加成本。
非线性与耦合性:工艺参数(如墨水浓度、液滴间距、基板温度、烧结温度/时间)与性能指标之间的关系高度非线性且相互耦合。
多模态性:可能存在多个不同的参数组合(即"山峰"),都能达到相似甚至相同的优良性能。传统优化方法可能只找到一个解,而忽视了其他等效的优质方案。
实验成本高:纳米银墨水昂贵,实验过程耗时。
解决方案:PSO-SVR + 多模态多目标优化
SVR(支持向量回归):充当"代理模型"或"预测器"。利用有限的实验数据,学习并建立起从"工艺参数"到"各项性能指标"的精确非线性映射关系。它可以预测新参数组合下的性能,从而大幅减少物理实验次数。
多目标粒子群优化(MOPSO):作为"优化引擎"。在SVR构建的预测模型所定义的"性能景观"中,同时搜索优化多个目标的参数空间。MOPSO能产生一组帕累托最优解集,即在这些解之间,无法再改进任何一个目标而不损害其他目标。
多模态处理:对标准MOPSO进行改进,使其能够识别和维持搜索空间中的多个等效帕累托最优解集(即不同的最优参数区域)。这对于工程师根据实际生产约束(如设备限制、偏好)选择不同方案至关重要。
二、 系统框架与实施步骤
整个流程可分为四个主要阶段:
阶段一:问题定义与数据准备
确定决策变量(工艺参数):例如,X = [墨水固含量(%), 打印层数, 液滴间距(μm), 基板温度(°C), 烧结温度(°C), 烧结时间(min), ...]。
确定优化目标:例如:
Minimize: 方阻(Ω/sq), 粗糙度(nm), 成本。
Maximize: 附着力, 线条均匀性, 拉伸率。
(注意:目标需可量化测量)。
设计实验(DOE)与数据采集:采用空间填充设计(如拉丁超立方采样)在参数空间内采样,进行物理实验,精确测量每个样本对应的所有目标值。形成数据集 {X_i, Y_i}。
阶段二:构建SVR代理模型
数据预处理:对输入参数和目标值进行归一化。
模型训练与验证:
为每个优化目标分别训练一个SVR模型。例如,一个SVR模型预测方阻,另一个预测附着力。
使用核函数(如RBF)处理非线性。
将数据集分为训练集和测试集,使用交叉验证和网格搜索优化SVR的超参数(C, gamma, epsilon)。
评估模型精度(R², RMSE),确保其预测可靠性足以替代大部分实验。
阶段三:集成多模态多目标PSO进行优化
定义适应度函数:将训练好的SVR模型组合起来,作为PSO中每个粒子的适应度评估函数。一个粒子代表一组工艺参数 X,将其输入各个SVR模型,得到对所有目标的预测值 Y_pred。
实施多模态MOPSO:
初始化:在参数边界内随机生成粒子群。
迭代更新:
评估每个粒子的适应度(通过SVR模型预测)。
更新个体最优(pbest)和全局最优(gbest)。在多目标中,"最优"概念变为"非支配"关系。
使用外部档案来存储迭代中发现的所有非支配解(帕累托前沿候选)。
引入多模态策略:
小生境技术:根据粒子在参数空间或目标空间的"距离"进行聚类。确保不同子群(小生境)能并行探索不同的潜在最优区域。
拥挤度比较:在档案维护和领导者选择时,优先选择稀疏区域的解,以维持解的多样性和覆盖不同的"山峰"。
根据速度-位置公式更新粒子位置。
终止:达到最大迭代次数或收敛标准后停止。
输出:获得一个多模态的帕累托最优解集。这个集合不仅包含了在目标空间上最优的折衷方案,其对应的参数解在参数空间中也可能是分散的(即多模态)。
阶段四:验证与决策
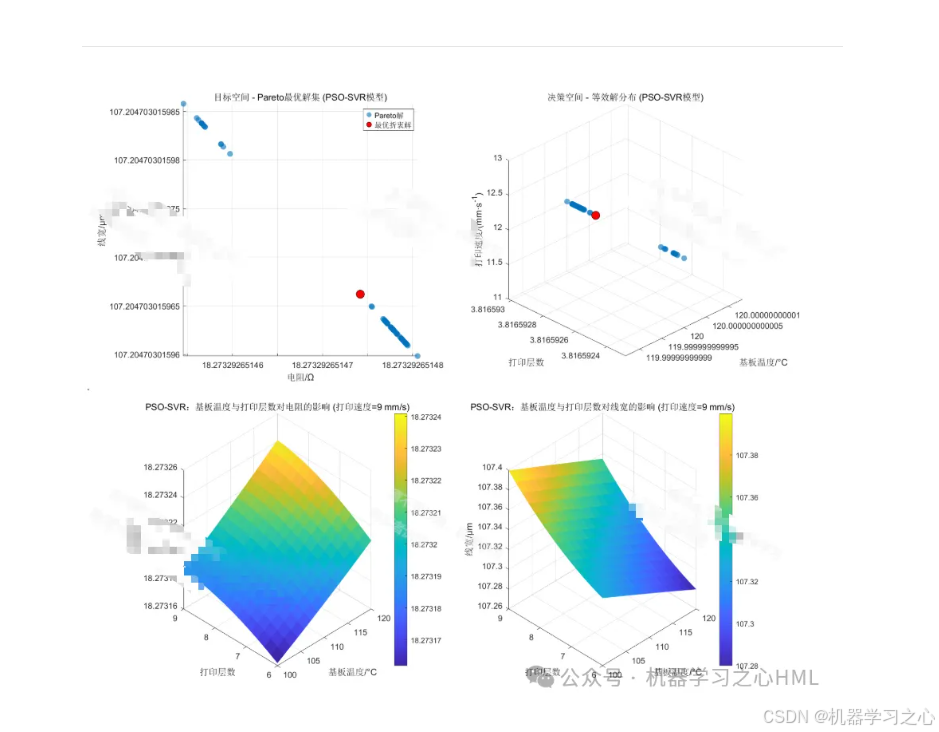
帕累托前沿分析:在目标空间中可视化最终的解集,展示各目标间的权衡关系。
多解选择:从帕累托解集中,根据实际生产偏好和约束(如"必须优先保证附着力 > XX N/mm"),选择几个有代表性的参数组合。
实验验证:对选出的少数几个最优参数组合进行物理实验验证,确认SVR预测的准确性及实际性能。这是闭环优化的关键一步。
三、 方法优势
高效性:用SVR代理模型替代大量耗时费钱的实验,优化过程在计算机上快速完成。
全面性:同时处理多个竞争性目标,提供一系列折衷方案,而非单一解。
发现性:多模态能力可以揭示"殊途同归"的多个工艺窗口,为工艺调整提供更多灵活性。
智能性:结合了机器学习(SVR)和智能优化算法(PSO)的优势,能处理高维非线性复杂问题。