一、研究背景
该代码研究背景为工业过程建模与优化 ,特别适用于锅炉排放预测 等物理约束明显的工业场景。传统数据驱动方法(如纯神经网络)往往忽略物理规律,容易在样本外区域失效。物理信息神经网络通过将物理方程或约束引入损失函数,提升模型的泛化性、可解释性和物理一致性。
二、主要功能
- 数据预处理:读取Excel数据、归一化、划分训练/测试集。
- PINN模型构建:构建具有物理约束的神经网络。
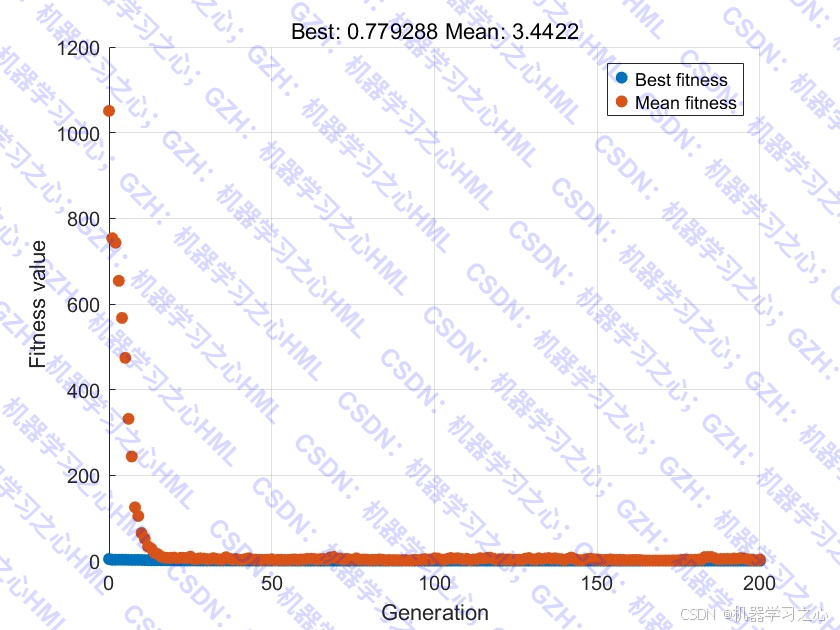
- 遗传算法优化:使用GA优化模型参数,遗传算法(GA)优化的是整个PINN模型的所有权重和偏置参数。
- 物理约束嵌入:通过合成样本和单调性标签引入领域知识。
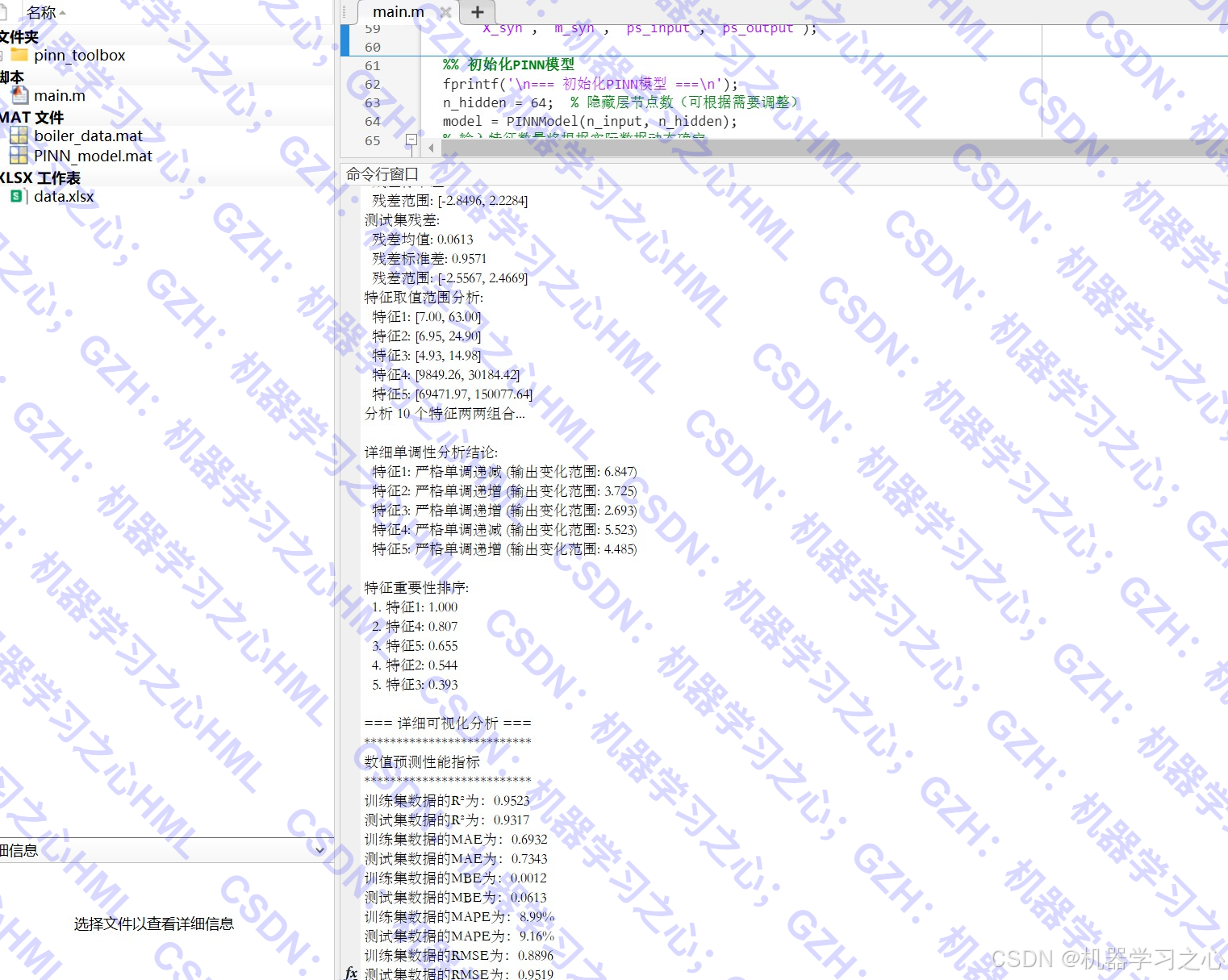
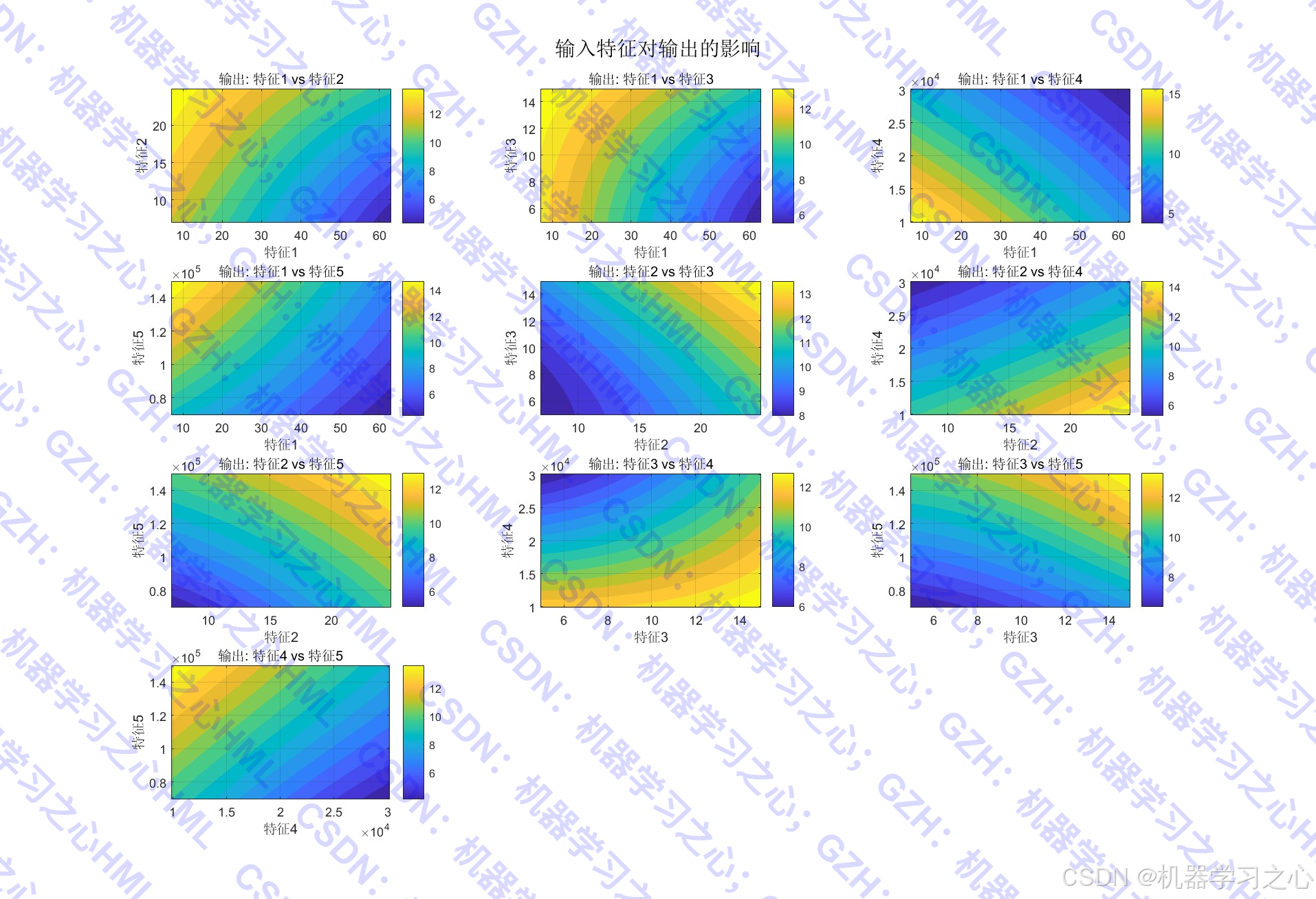
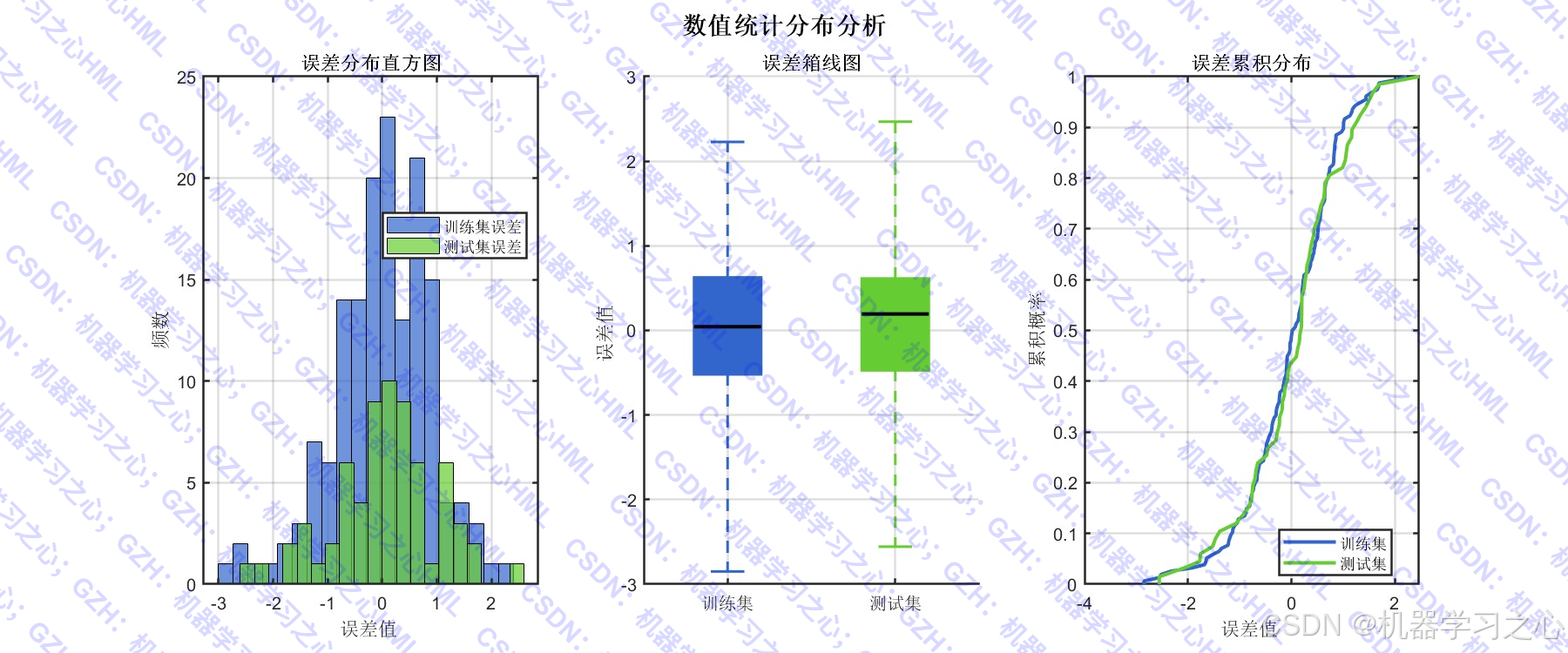
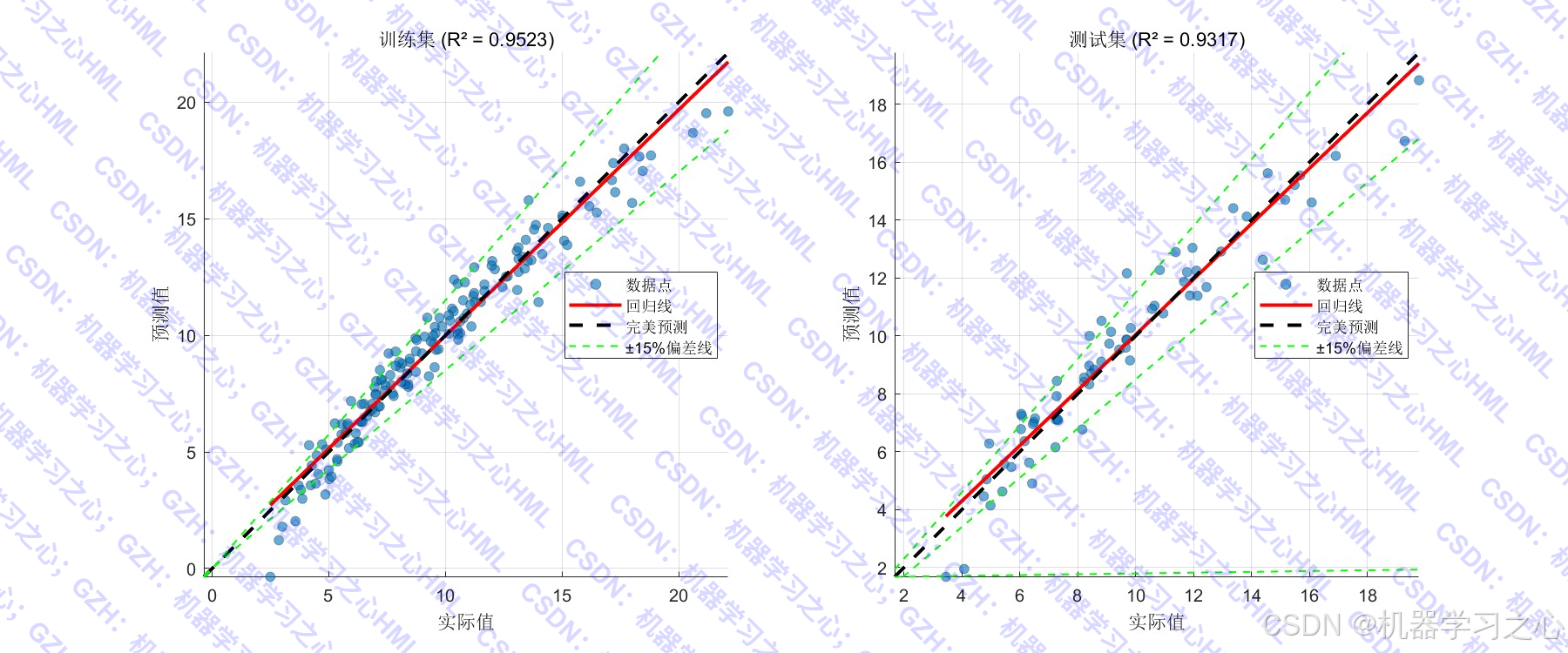
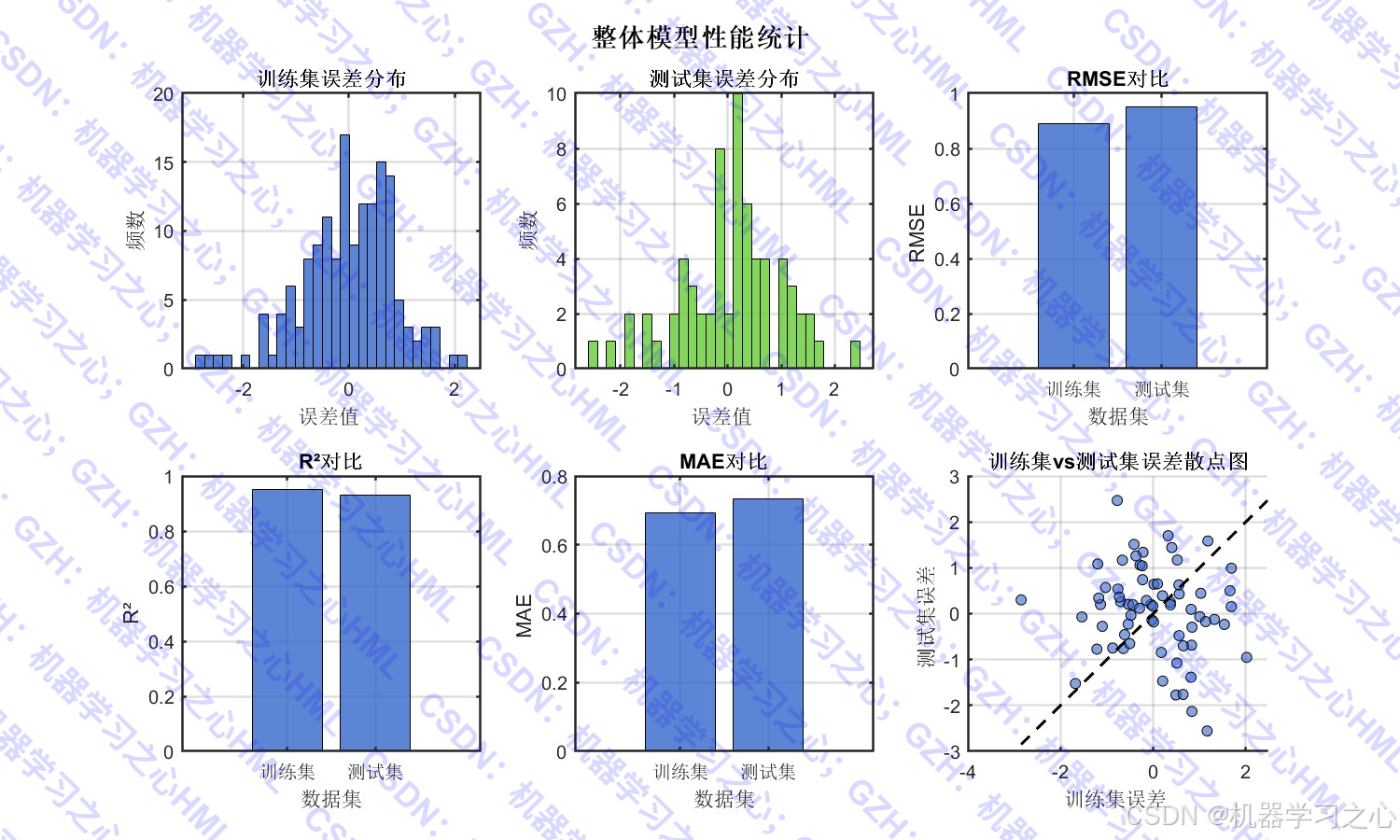
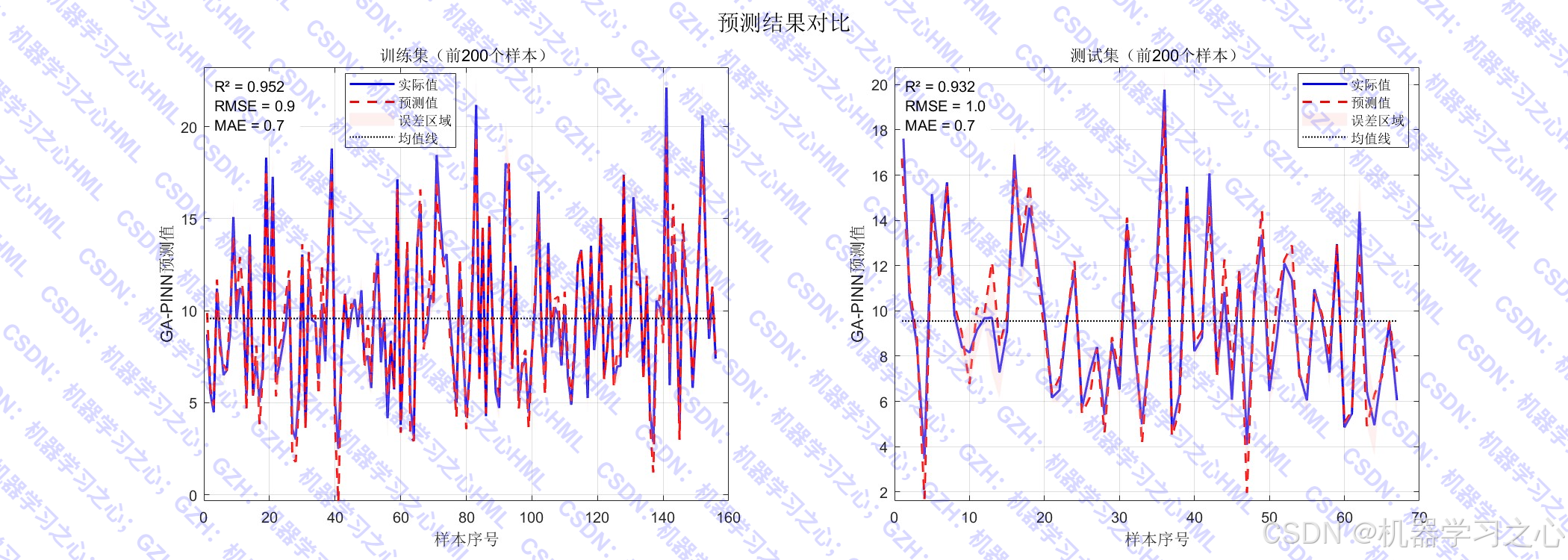
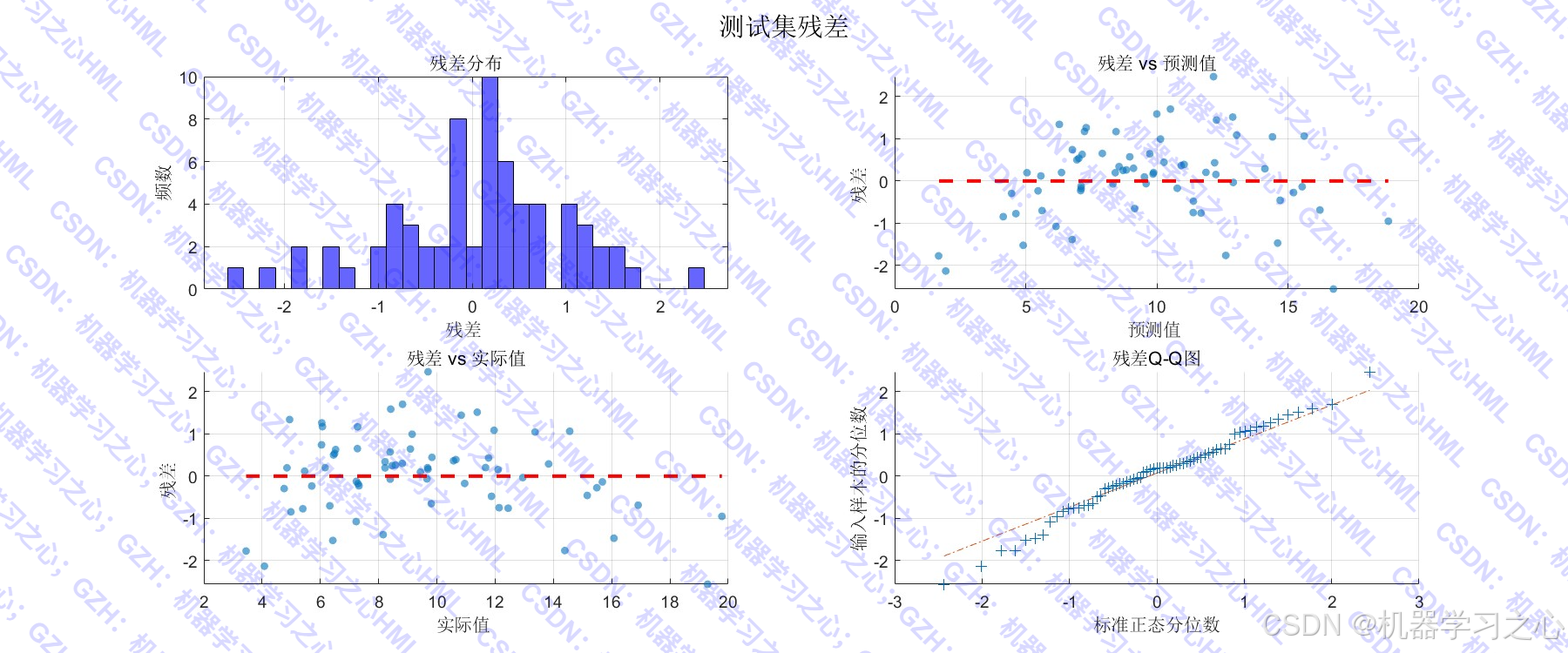
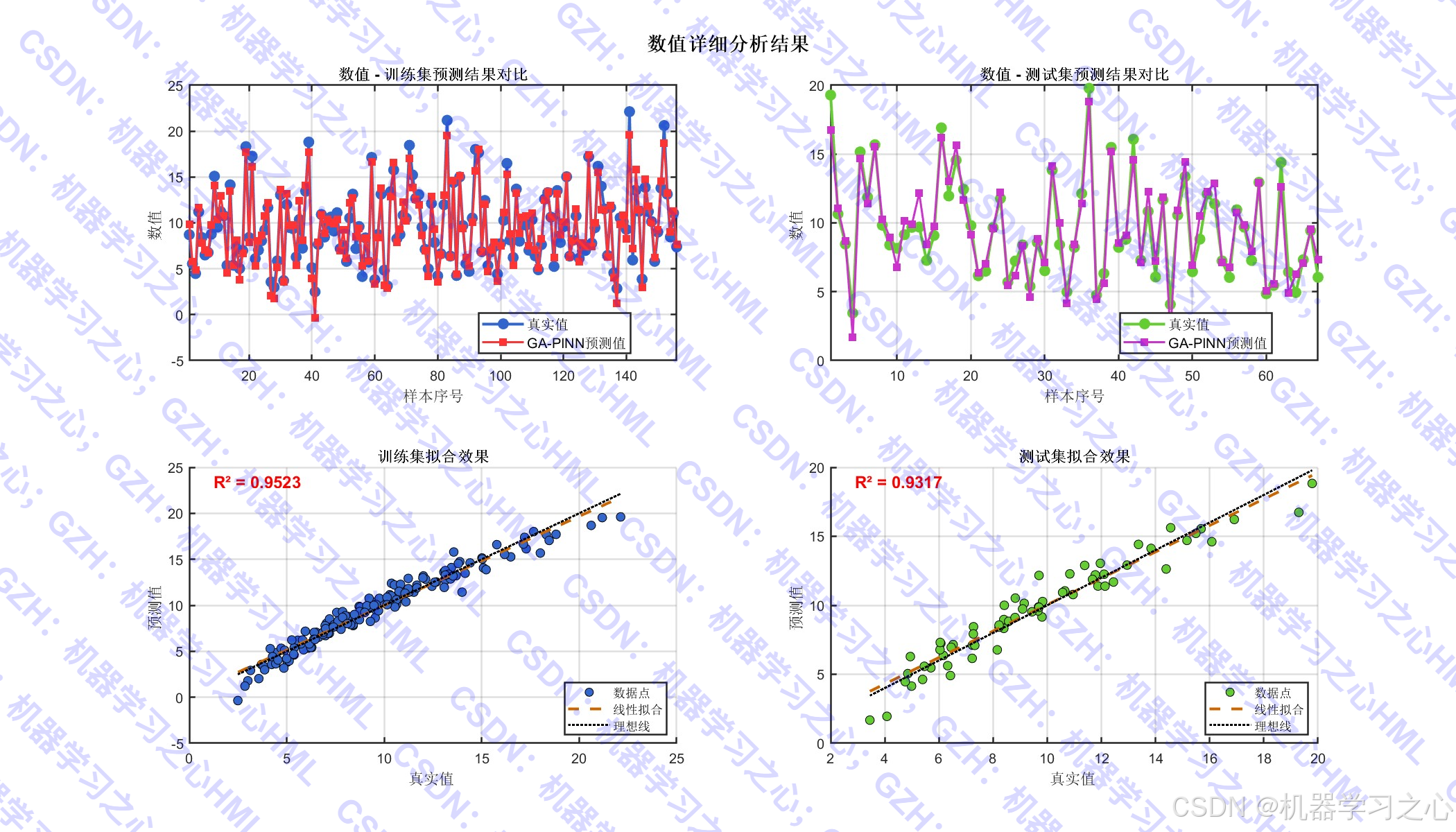
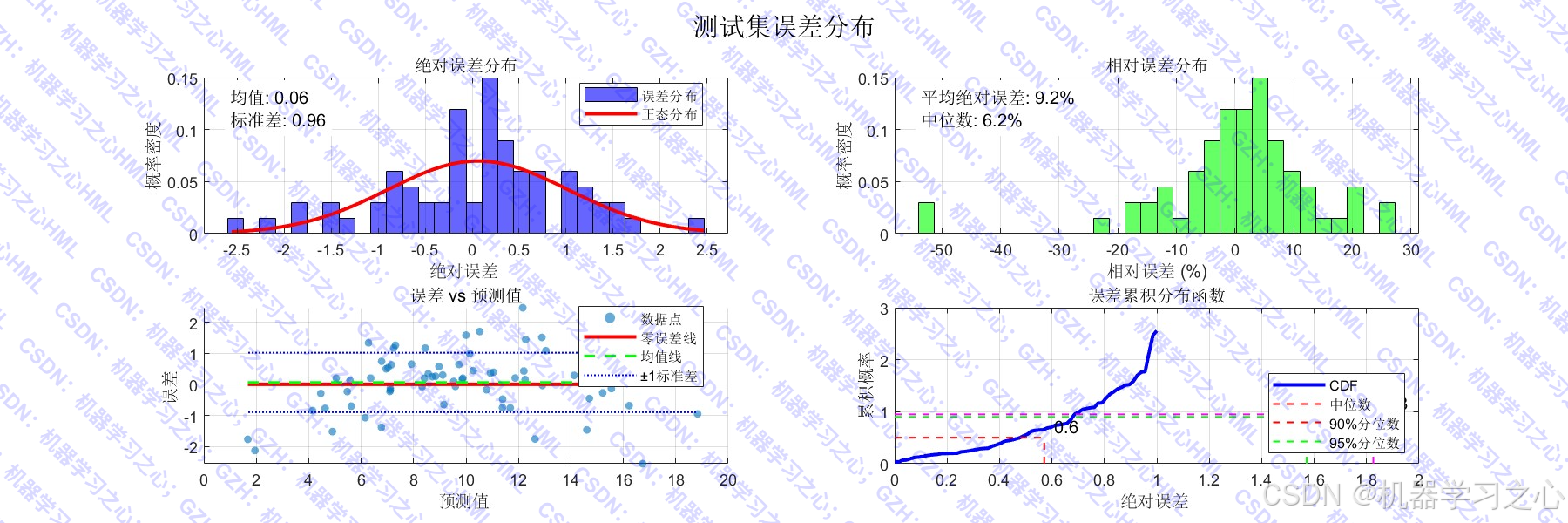
- 模型评估与可视化:计算R²、RMSE、MAE等指标,绘制预测对比图、误差分布图等。
三、算法步骤
- 数据准备:导入数据 → 随机打乱 → 归一化 → 划分训练/测试集。
- 合成样本生成:基于训练数据分布生成带物理标签的合成样本。
- PINN模型初始化:构建含一个隐藏层的神经网络(输入→隐藏→输出)。
- 损失函数定义 :
- 回归损失(MSE)
- 结构损失(L2正则化)
- 物理不一致性损失(单调性约束)
- 遗传算法优化:使用GA搜索最优模型参数。
- 模型评估:反归一化预测结果 → 计算评估指标 → 可视化分析。
四、技术路线
数据驱动 + 物理引导 → 混合建模
GA(全局搜索) + PINN(物理约束) → 优化模型
前向神经网络 + 梯度惩罚 → 物理一致性五、公式原理
1. 总损失函数:
L=Er+λsEs+λpEp L = E_r + \lambda_s E_s + \lambda_p E_p L=Er+λsEs+λpEp
- Er=∑(ypred−ytrue)2E_r = \sum (y_{pred} - y_{true})^2Er=∑(ypred−ytrue)2:回归损失
- Es=∑θ2E_s = \sum \theta^2Es=∑θ2:结构损失(L2正则化)
- Ep=∑i1−mi⋅sign(∂y∂xi)2E_p = \sum_{i} \frac{1 - m_i \cdot \text{sign}(\frac{\partial y}{\partial x_i})}{2}Ep=∑i21−mi⋅sign(∂xi∂y):物理不一致性损失
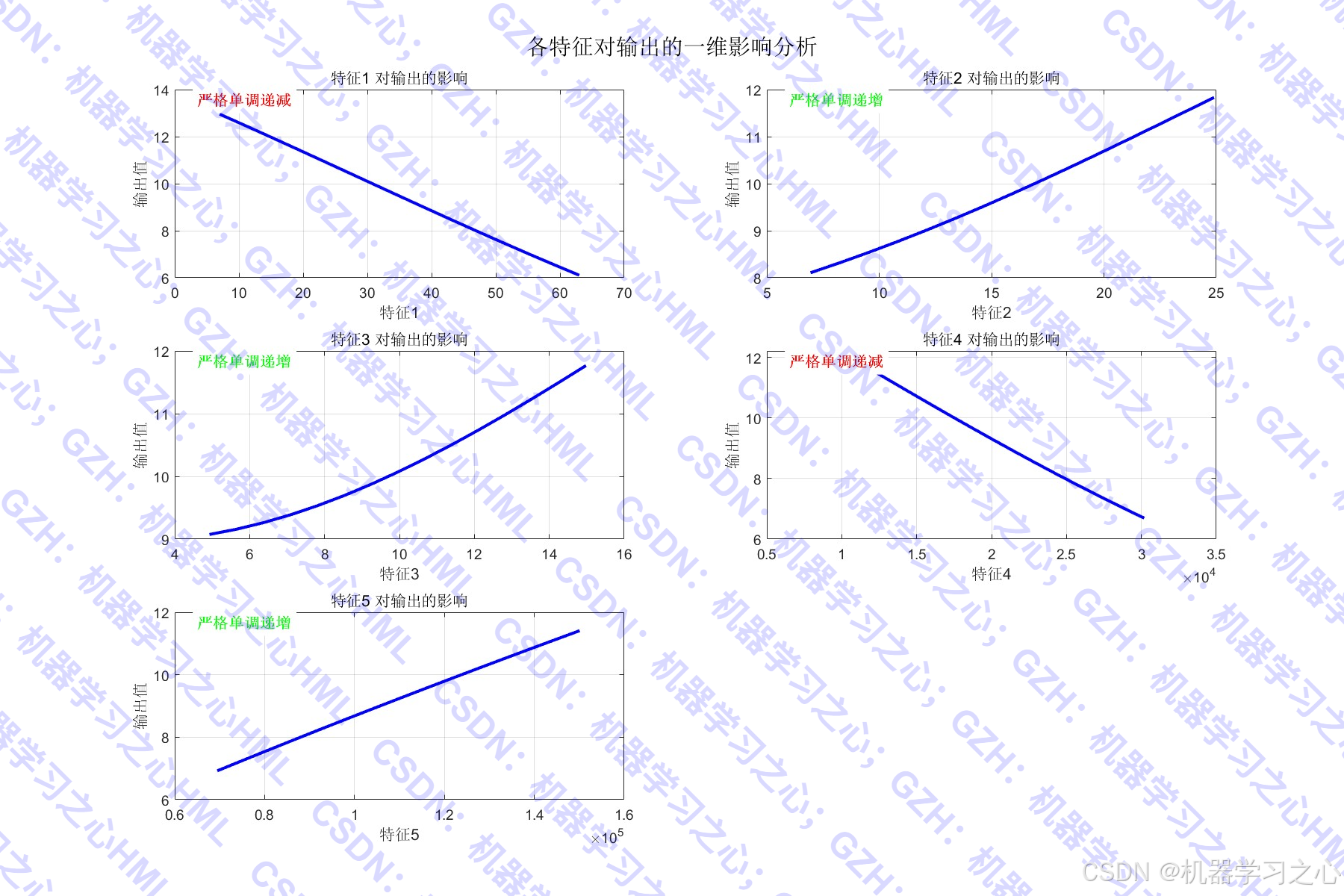
2. 物理约束(单调性):
mi⋅∂y∂xi≥0 m_i \cdot \frac{\partial y}{\partial x_i} \geq 0 mi⋅∂xi∂y≥0
其中mi∈{+1,0,−1}m_i \in \{+1,0,-1\}mi∈{+1,0,−1} 表示该特征与输出之间的期望单调关系。
六、参数设定
| 参数 | 值/说明 |
|---|---|
| 隐藏层节点数 | 64 |
| 训练集比例 | 70% |
| 遗传算法迭代次数 | 200 |
| 种群大小 | 100 |
| 物理损失权重 λp\lambda_pλp | 0.001 |
| 结构损失权重 λs\lambda_sλs | 0.001 |
| 合成样本数量 | 300 |
| 归一化方法 | mapminmax(归一化到[0,1]) |
七、运行环境
- 平台:MATLAB2024b
- 数据文件:
data.xlsx
八、应用场景
- 工业过程建模:锅炉排放、能耗预测、工艺优化。
- 物理约束回归:需要模型输出符合物理规律的任务。
- 小样本学习:通过物理约束提升模型在数据稀缺区域的性能。
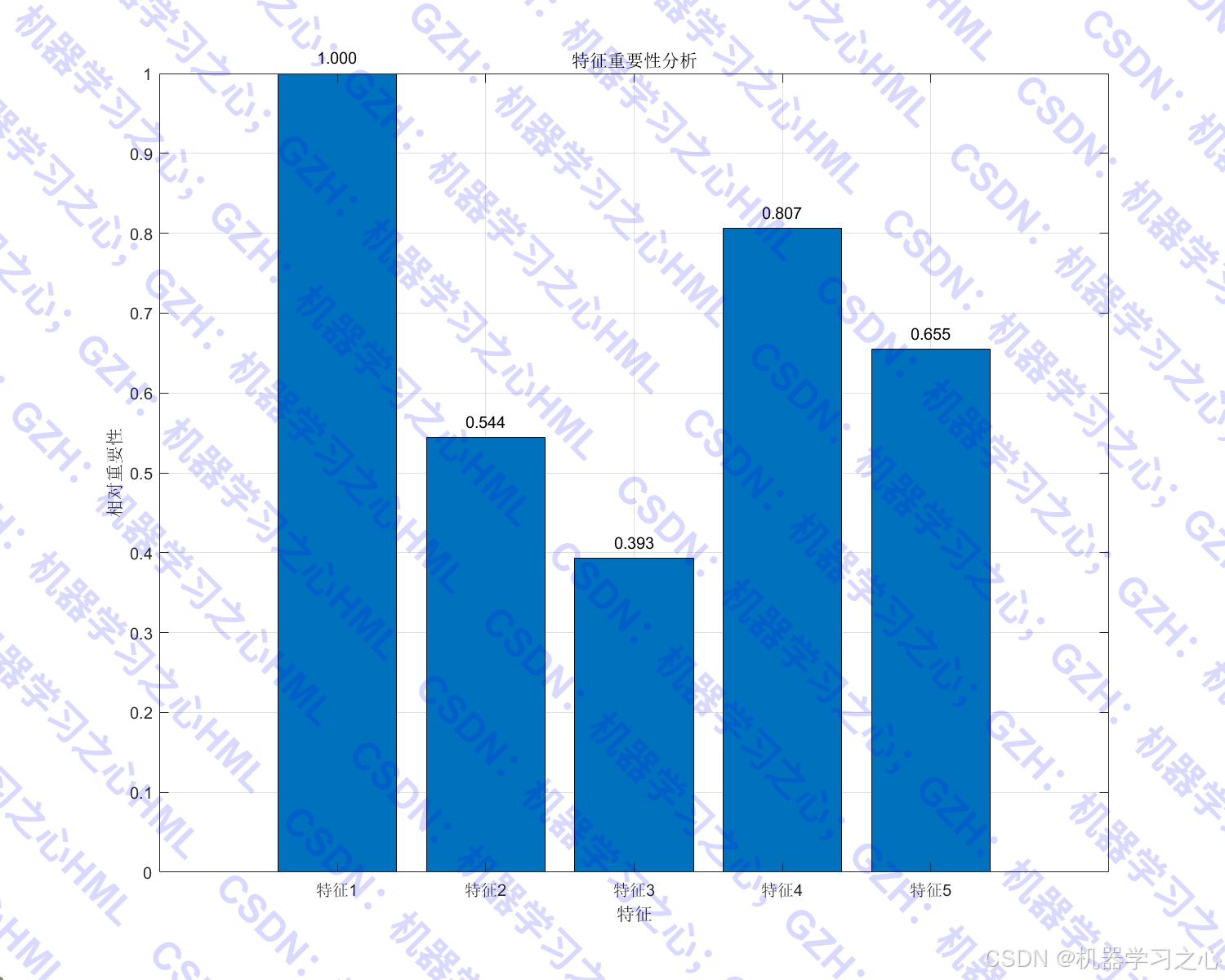
- 可解释性AI:通过梯度分析输入输出关系,符合领域认知。
总结
该代码是一个完整的GA-PINN回归预测框架,将数据驱动与物理约束有机结合,适用于需要模型具备物理一致性的工业预测任务。