B树的由来
大量的数据首先存储位置在磁盘上,数据需要读取到内存中,再让内存和cpu进行交换,我们只需关心访问延迟,内存它的访问延迟纳秒为单位,磁盘的访问延迟在亳秒为单位,1秒==10~3毫秒==10~9纳秒,相当于磁盘的访问延迟是内存的100W倍。
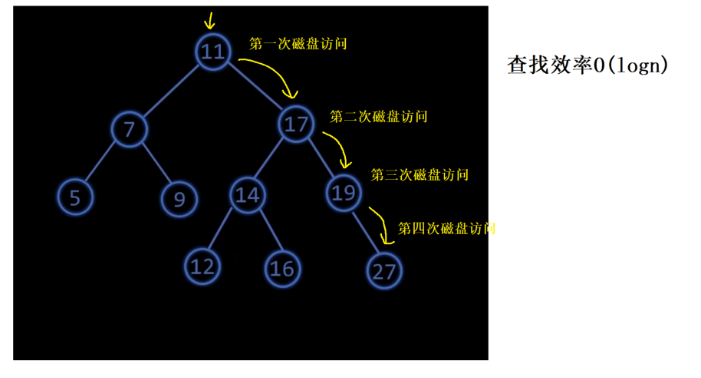
怎么能降低磁盘访问次数?现在一个有效节点里面只存储一个有效值,如果一个有效节点可以存储多个有效值,这这时同样的数据量,则节点更加胖,但是组织架构会更加的扁平,也就是树的高度会降低。
B树的概念
1.平衡:所有的叶子节点都在同一层
2.有序:节点内部是有序递增的,且任意元素的左子树都小于它,右子树都大于它
3.多路:一个节点可以向外伸出M个手(M是阶数)
节点分支的上限:根节点上限是M/非根节点上限是M
节点分支的下限:根节点下限是2/非根节点上限是[M/2]
节点内部元素个数的上限:根节点上限是M-1个/非根节点上限是M-1个
节点内部元素个数的下限:根节点上限是1个/非根节点上限是[M/2]-1个
B树的节点定义
typedef int ELEMTYPE;
#define M 5
typedef struct BTNode {
int key_num;
ELEMTYPE key_arr[M + 1];
BTNode* prt_arr[M + 1];
}BTNode;
typedef struct BTree {
struct BTNode* root;
}Btree;
typedef struct Result {
bool tag;
struct BTNode* pNode;
int index;
}Result;变量M为该B树为M阶B树
BTNode结构体中的key_num为该节点存储的多少个元素
key_arr为存储的值
prt_arr为其数组的左右子树。
Result结构体为返回的结构体节点数据。
B树的工具函数
购买节点函数
BTNode* BT_Buy_Node()
{
BTNode* p = (BTNode*)malloc(sizeof(BTNode));
if (p == nullptr)return NULL;
memset(p,0, sizeof(p));
return p;
}
Result* BR_Buy_Node()
{
Result* result = (Result*)malloc(sizeof(Result));
if (result == NULL)
exit(EXIT_FAILURE);
result->index = 0;
result->pNode = NULL;
result->tag = false;
return result;
}B树的插入
插入主函数
bool Insert_BTree(Btree* pTree, ELEMTYPE key)
{
assert(pTree != NULL);
if (pTree->root == NULL)
{
pTree->root = BT_Buy_Node();
pTree->root->key_arr[0] = key;
pTree->root->key_num = 1;
return true;
}
Result* pr = Search_BTree(pTree, key);
if (pr->tag)return true;
memmove(pr->pNode->key_arr + pr->index + 1, pr->pNode->key_arr + pr->index, sizeof((pr->pNode->key_num - pr->index) * sizeof(ELEMTYPE)));
pr->pNode->key_arr[pr->index] = key;
pr->pNode->key_num++;
if (pr->pNode->key_num == M) {
BT_Insert_Adjust(pTree, pr->pNode);
}
return true;
}插入调整函数
void BT_Insert_Adjust(Btree* pTree, BTNode* Node)
{
assert(pTree != NULL);
while (Node->key_num >= M) {
Node= BT_SplitNode(pTree, Node);
}
if (Node->key_num == 1) {
pTree->root = Node;
}
}插入分裂函数
BTNode* BT_SplitNode(BTree* pTree, BTNode* Node)
{
BTNode* movenode = BT_Buy_Node();
int r = 0;
for (int i = Node->key_num / 2+1; i < Node->key_num; i++) {
movenode->key_arr[r++] = Node->key_arr[i];
movenode->key_num++;
}
Node->key_num -= movenode->key_num+1;
r = 0;
for (int i = M / 2 + 1; i <= Node->key_num; i++) {
movenode->prt_arr[r++] = Node->prt_arr[i];
//分裂的不是叶子节点
if (movenode->prt_arr[i] != NULL) {
movenode->prt_arr[i]->parent = movenode;
}
}
BTNode* p = Node->parent;
ELEMTYPE tmp = Node->key_arr[M / 2];
if (p == NULL) {
BTNode* newroot = BT_Buy_Node();
newroot->key_arr[0] = tmp;
newroot->key_num = 1;
newroot->prt_arr[0] = Node;
newroot->prt_arr[1] = movenode;
Node->parent = newroot;
movenode->parent = newroot;
return newroot;
}
//注意r要从key_num开始,从0开始如果小于tmp直接跳出,并没由移动之前的值
r = p->key_num;
for (r; r > 0; r--) {
if (p->key_arr[r-1] > tmp) {
p->key_arr[r] = p->key_arr[r-1];
}
else {
break;
}
}
p->key_arr[r] = tmp;
/*p->prt_arr[r + 2] = p->prt_arr[r + 1];*/
memmove(p->prt_arr + 2 + r, p->prt_arr + r + 1, sizeof(p->prt_arr) * p->key_num - r);
p->prt_arr[r+1] = movenode;
p->key_num++;
movenode->parent = p;
return p;
}B树的删除
删除主函数
bool Delete_BTree(Btree* pTree, ELEMTYPE key)
{
assert(pTree != NULL);
Result* pr = Search_BTree(pTree, key);
if (!pr->tag) {
return true;
}
//判断是否为叶子节点
if (pr->pNode->prt_arr[0] != NULL) {
BTNode* cat = pr->pNode->prt_arr[pr->index+1];
while (cat->prt_arr[0] != NULL) {
cat = cat->prt_arr[0];
}
pr->pNode->key_arr[pr->index] = cat->key_arr[0];
pr->pNode = cat;
pr->index = 0;
}
//此时删除的是叶子节点
BTNode* p = pr->pNode;
for (int i = pr->index+1; i < p->key_num; i++) {
p->key_arr[i - 1] = p->key_arr[i];
}
p->key_num--;
//此时有四种情况
if ((p->parent == NULL && p->key_num >= 1) || (p->parent != NULL && p->key_num >= M / 2)) {
return true;
}
if (p->parent == NULL && p->key_num == 0)
{
free(p);
free(pr);
pTree->root = NULL;
return true;
}
BT_Delete_Adjust(pTree, p);
}删除调整函数
void Delete_Adjust(BTree* pTree, BTNode* Node)
{
//0.assert
//1.申请一个指针,用来指向Node的父节点
BTNode* father = Node->parent;
//2.方法1:通过Node地址的比较,判断出,当前Node在父节点中第几个下标上
// 方法2:通过Node的元素比较,判断出,当前Node在父节点中第几个下标上
//用2:思路就是父节点里面找第一个大于我当前Node节点里的第一个元素的值
int i = 1;
for (; i <= father->key_num; i++)
{
if (father->keys[i] > Node->keys[1])//找到了第一个大于我当前Node节点里的元素的值
{
break;
}
}
//3.再申请两个指针,用来指向Node的左右兄弟
//注意:左右兄弟是有可能不存在的
BTNode* LeftBro = i - 2 >= 0 ? father->ptr[i - 2] : NULL;
BTNode* RightBro = i <= father->key_num ? father->ptr[i] : NULL;
//如果真的下溢出了,观察其左右兄弟是否存在且够借,如果够借,则问兄弟借,直接结束(口诀:父下来,兄上去)
//4.尽量先看左兄弟是否存在且够借,如果存在且够借,则直接先问左兄弟借
if (LeftBro != NULL && LeftBro->key_num > M / 2)
{
BorrowFrom_LeftBro(father, i - 1);
return;
}
//5.再问右兄弟借(如果右兄弟存在且够借的情况下)
else if (RightBro != NULL && RightBro->key_num > M / 2)
{
BorrowFrom_RightBro(father, i);
return;
}
//6.执行到这里,就说明左右兄弟要么不存在,要么存在但是不够给我借元素
else
{
//7.只能和左右兄弟进行合并了(口诀:父下左,右靠左)
//7.5 准备工作:申请一个指针ptr,用来接收合并操作返回的合并的节点
BTNode* ptr = NULL;
//8.1 只有左兄弟存在-->只能和左兄弟合并
//8.2 左右兄弟都存在-->和左兄弟合并
if (LeftBro != NULL)
{
ptr = Merge_LeftBro(father, i - 1);
}
//8.3 只有右兄弟存在-- > 只能和右兄弟合并
else
{
ptr = Merge_RightBro(father, i);
}
//注意:非根节点,不会存在左右兄弟都不存在的情况,至少得有一个兄弟存在
//9.合并操作是会导致父节点缺少一个元素,所以可能会导致父节点出现连续的
// 下溢出,则小心判断父节点,看是否需要继续处理
//9.1 father是根节点 -> 溢出 -> 调整处理
//10.特殊情况:如果合并操作导致根节点空了,没有元素了,则需要释放此时的根节点,让刚刚合并的节点看做新的根节点即可
if (father->parent == NULL && father->key_num < 1)
{
free(father);
pTree->root = ptr;
ptr->parent = NULL;
}
//9.2 father是非根节点 -> 溢出 -> 调整处理
else if (father->parent != NULL && father->key_num < M / 2)
{
Delete_Adjust(pTree, father);
}
//9.3 father是根节点 -> 没有溢出 -> 不需要调整处理
//9.4 father是非根节点 -> 没有溢出 -> 不需要调整处理
else
{
return;
}
}
}左兄弟借函数
void BT_BorrowFrom_LeftBro(BTNode* pp, int index)
{
assert(index >= 0 && index < pp->key_num);
BTNode* child = pp->prt_arr[index];
BTNode* leftBro = pp->prt_arr[index - 1];
for (int i = child->key_num-1; i >= 0; i--)
child->key_arr[i + 1] = child->key_arr[i];
child->key_arr[0] = pp->key_arr[index];
if (leftBro->prt_arr[0] != NULL)
{
for (int i = child->key_num; i >= 0; i--)
child->prt_arr[i + 1] = child->prt_arr[i];
child->prt_arr[0] = leftBro->prt_arr[leftBro->key_num];
}
pp->key_arr[index] = leftBro->key_arr[leftBro->key_num-1];
child->key_num += 1;
leftBro->key_num -= 1;
}右兄弟借函数
//8.从右兄弟借
void BorrowFrom_RightBro(BTNode* pp, int index)
{
assert(index >= 1 && index <= pp->key_num);
//1.先通过pp和index找到自己和右兄弟节点
BTNode* child = pp->ptr[index-1];
BTNode* rightBro = pp->ptr[index];
//2.将父节点的值拉下来(口诀:父下来)
child->keys[child->key_num+1] = pp->keys[index];
//3.将兄弟节点的值,挪上去到父节点
pp->keys[index] = rightBro->keys[1];
//4.若如果兄弟不是叶子结点(换句话说,兄弟有子树)
//则把右兄弟的第一个孩子指针域,挪动到自己的最后一个指针域位置
if (rightBro->ptr[0] != NULL)
{
child->ptr[child->key_num+1] = rightBro->ptr[0];
}
//5.修正右兄弟节点的元素值和孩子指针域
for (int i = 2; i <= rightBro->key_num; i++)
rightBro->keys[i - 1] = rightBro->keys[i];
for (int i = 1; i <= rightBro->key_num; i++)
rightBro->ptr[i - 1] = rightBro->ptr[i];
//6.修正更新各个节点的有效元素个数
child->key_num += 1;
rightBro->key_num -= 1;
}左兄弟合并函数
BTNode* Merge_LeftBro(BTNode* pp, int index)
{
//0.assert
assert(pp != NULL);
// 口诀:父下左,右靠左
//1.申请两个指针Node和LeftNode用来指向自己和需要和自己合并的左兄弟
BTNode* LeftNode = pp->ptr[index-1];
BTNode* Node = pp->ptr[index];
//2.将Node和LeftNode在父节点中夹着的那个元素,挪下来,挪到左侧的LeftNode节点的屁股后边(父下左)
LeftNode->keys[LeftNode->key_num+1] = pp->keys[index];
//3.更新一下LeftNode节点的元素个数,因为一会后边要用到LeftNode.key_num这个参数
LeftNode->key_num++;
//4.再将右侧的Node的全部有效元素给到左侧的LeftNode
for (int i = 1; i <= Node->key_num; i++)//i指向的合并的右侧节点Node的元素下标
{
LeftNode->keys[LeftNode->key_num + i] = Node->keys[i];
}
//5.再将右侧的Node的全部孩子指针域给到左侧的LeftNode自己(特别注意:如果右侧节点的
// 孩子指针不为NULL,也就是说其孩子指针指向的是确确实实存在的节点,那么你需要考虑
// 把它这下孩子的双亲指针也修正一下)
for (int i = 0; i <= Node->key_num; i++)//i指向的合并的右侧节点Node的孩子指针域下标
{
if (Node->ptr[i] != NULL)
{
LeftNode->ptr[LeftNode->key_num+i] = Node->ptr[i];
Node->ptr[i]->parent = LeftNode;
}
}
//6.修正父节点现有的元素及其的剩余的孩子指针域统一向前挪动一下
for (int i = index + 1; i <= pp->key_num; i++)
{
pp->keys[i - 1] = pp->keys[i];
pp->ptr[i - 1] = pp->ptr[i];
}
//7.修正各个其他节点的有效元素个数
LeftNode->key_num += Node->key_num;
pp->key_num -= 1;
//8.释放右侧的Node节点
free(Node);
//9.将合并之后的节点返回出去(返回的是左侧的LeftNode)
return LeftNode;
}右兄弟合并函数
BTNode* Merge_RightBro(BTNode* pp, int index)
{
//0.assert
assert(pp != NULL);
// 口诀:父下左,右靠左
//1.申请两个指针Node和RightNode用来指向自己和需要和自己合并的右兄弟
BTNode* Node = pp->ptr[index - 1];
BTNode* RightNode = pp->ptr[index];
//2.将Node和RightNode在父节点中夹着的那个元素,挪下来,挪到左侧的Node节点的屁股后边(父下左)
Node->keys[Node->key_num + 1] = pp->keys[index];
//3.更新一下Node节点的元素个数,因为一会后边要用到Node.key_num这个参数
Node->key_num++;//这一步非常重要 一定在这里修正好
//4.再将右侧的RightNode的全部有效元素给到左侧的Node自己
for (int i = 1; i <= RightNode->key_num; i++)
{
Node->keys[Node->key_num+i] = RightNode->keys[i];
}
//5.再将右侧的RightNode的全部孩子指针域给到左侧的Node自己(特别注意:如果右侧节点的
// 孩子指针不为NULL,也就是说其孩子指针指向的是确确实实存在的节点,那么你需要考虑
// 把它这下孩子的双亲指针也修正一下)
for (int i = 0; i <= RightNode->key_num; i++)
{
if (RightNode->ptr[i] != NULL)
{
RightNode->ptr[i]->parent = Node;
Node->ptr[Node->key_num + i] = RightNode->ptr[i];
}
}
//6.修正父节点现在的元素及其的剩余的孩子指针域统一向前挪动一下
for (int i = index + 1; i <= pp->key_num; i++)
{
pp->keys[i-1] = pp->keys[i];//挪动剩余元素
pp->ptr[i-1] = pp->ptr[i];//挪动剩余孩子指针域
}
//7.修正各个其他节点的有效元素个数
Node->key_num = Node->key_num + RightNode->key_num;
pp->key_num -= 1;
//8.释放右侧的RightNode节点
free(RightNode);
//9.将合并之后的节点返回出去(左侧的Node)
return Node;
}B树的查找
Result* Search_BTree(BTree* root, ELEMTYPE val)
{
assert(root != NULL);
BTNode* p = root->root;
BTNode* pp = NULL;
int i = 0;
Result* node = BR_Buy_Node();
while (p != nullptr) {
i = 0;
while (i < p->key_num) {
if (val > p->key_arr[i]) {
i++;
}
else if (val == p->key_arr[i]) {
node->tag = true;
node->index = i;
node->pNode = p;
return node;
}
else {
pp = p;
p = p->prt_arr[i];
break;
}
}
if (i == p->key_num) {
pp = p;
p = p->prt_arr[i];
}
}
node->pNode = pp;
node->index = i;
return node;
}B树的打印
void Show_InOrder1(BTNode* node)
{
if (node == nullptr)return;
int i = 0;
for (; i < node->key_num; i++) {
if (node->prt_arr[i] != nullptr) {
Show_InOrder1(node->prt_arr[i]);
continue;
}
printf("%d ", node->key_arr[i]);
}
if (node->prt_arr[i] != nullptr) {
Show_InOrder1(node->prt_arr[i]);
}
}