【机器学习】BP神经网络

目录

一、引言

二、算法前置定义（符号系统）

[三、BP 神经网络核心算法步骤](#三、BP 神经网络核心算法步骤)

[步骤 1：网络参数初始化](#步骤 1：网络参数初始化)

[步骤 2：前向传播（Forward Propagation）](#步骤 2：前向传播（Forward Propagation）)

[2.1 隐藏层输入与输出](#2.1 隐藏层输入与输出)

[2.2 输出层输入与输出](#2.2 输出层输入与输出)

[步骤 3：计算损失函数（Loss Function）](#步骤 3：计算损失函数（Loss Function）)

[3.1 二分类任务（垃圾邮件检测）：二元交叉熵损失](#3.1 二分类任务（垃圾邮件检测）：二元交叉熵损失)

[3.2 多分类任务：类别交叉熵损失](#3.2 多分类任务：类别交叉熵损失)

[3.3 回归任务：均方误差（MSE）损失](#3.3 回归任务：均方误差（MSE）损失)

[步骤 4：反向传播（Backward Propagation）](#步骤 4：反向传播（Backward Propagation）)

[4.1 定义 "误差项"](#4.1 定义 “误差项”)

[4.2 输出层误差项（​编辑​）](#4.2 输出层误差项（编辑）)

[4.3 隐藏层误差项（​编辑​）](#4.3 隐藏层误差项（编辑）)

[4.4 计算权重与偏置的梯度](#4.4 计算权重与偏置的梯度)

[步骤 5：参数更新（梯度下降）](#步骤 5：参数更新（梯度下降）)

[步骤 6：迭代训练与终止条件](#步骤 6：迭代训练与终止条件)

[四、BP 神经网络的Python代码完整实现](#四、BP 神经网络的Python代码完整实现)

五、程序运行结果展示

六、总结

---

一、引言

BP 神经网络（Back Propagation Neural Network）是多层前馈神经网络 的核心训练算法，核心逻辑是：前向传播计算预测输出与损失，反向传播通过链式法则计算参数梯度，再用梯度下降更新权重 / 偏置，最终最小化预测误差。本文将详细讲解BP神经网络的算法原理以及Python代码完整实现。

二、算法前置定义（符号系统）

先统一核心符号，避免公式歧义（以 "输入层 + 1 层隐藏层 + 输出层" 的经典结构为例，多层隐藏层可类推）：

符号	含义
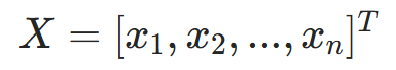	输入层向量，维度 n（n 为输入层神经元数，对应文本任务的 TF-IDF 特征数）
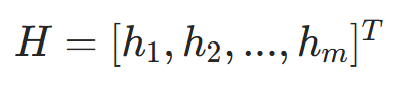	隐藏层输出向量，维度 m（m 为隐藏层神经元数）
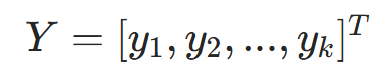	输出层预测向量，维度 k（k 为输出层神经元数，二分类k=1，多分类k=类别数）
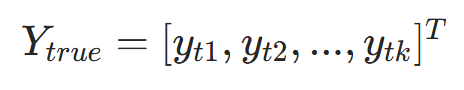	真实标签向量
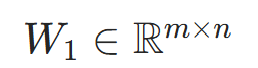	输入层→隐藏层的权重矩阵（第i行第j列：输入层第j个神经元到隐藏层第i个神经元的权重）
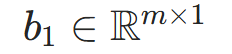	隐藏层的偏置向量
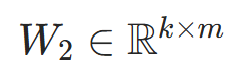	隐藏层→输出层的权重矩阵
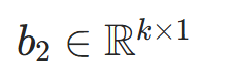	输出层的偏置向量
σ(⋅)	激活函数（隐藏层常用 ReLU/Tanh/Sigmoid，输出层二分类用 Sigmoid、多分类用 Softmax）
L	损失函数（衡量预测值与真实值的差距）
η	学习率（控制参数更新步长）
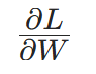	损失函数对权重W的梯度（反向传播核心计算目标）

三、BP 神经网络核心算法步骤

步骤 1：网络参数初始化

神经网络的权重 / 偏置不能初始化为全 0（会导致所有神经元输出相同，梯度消失），需初始化为「随机小值」：

• 权重初始化：常用「正态分布初始化」（W∼N(0,0.01)）或「Xavier 初始化」（适配 Tanh/Sigmoid）、「He 初始化」（适配 ReLU）；
• 偏置初始化：通常初始化为 0 或小常数（如b=0.1）。

示例（输入层n=100，隐藏层m=32，输出层k=1）：

步骤 2：前向传播（Forward Propagation）

从输入层到输出层逐层计算神经元输出，核心是 "线性变换 + 激活函数"：

2.1 隐藏层输入与输出

隐藏层的「净输入」（线性变换结果）：

​

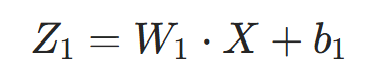
隐藏层的「输出」（净输入经过激活函数）：

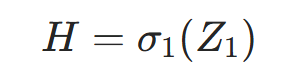
• 激活函数选择（隐藏层）：
  • Sigmoid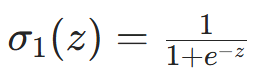：（值域(0,1)，易梯度消失，适合小数据）；
  • ReLU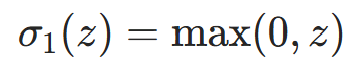：（计算快，缓解梯度消失，主流选择）；
  • Tanh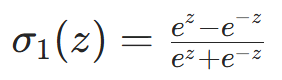：（值域(−1,1)，中心化输出）。

2.2 输出层输入与输出

输出层的「净输入」：

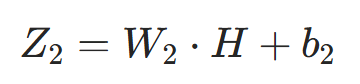
输出层的「输出」（根据任务选激活函数）：

• 二分类任务（如垃圾邮件检测）：Sigmoid 激活
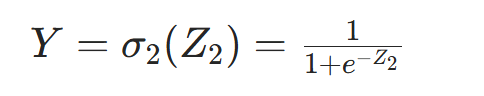
• 多分类任务（如文档分类）：Softmax 激活
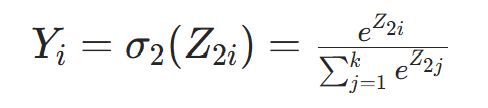
• 回归任务：无激活函数（直接输出Z2）。

步骤 3：计算损失函数（Loss Function）

损失函数是 "预测值与真实值的差距量化"，反向传播的核心目标是最小化损失函数。

3.1 二分类任务（垃圾邮件检测）：二元交叉熵损失

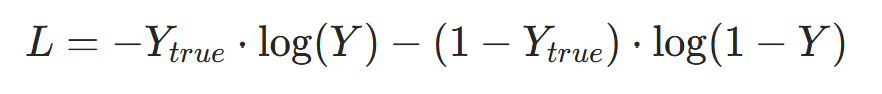
• 若样本数为N，批量损失为所有样本损失的均值：

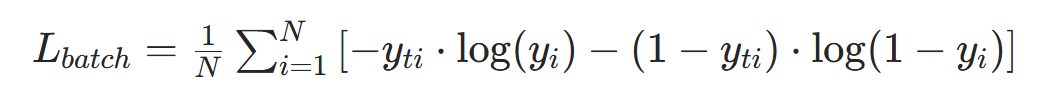
3.2 多分类任务：类别交叉熵损失

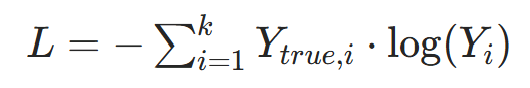
3.3 回归任务：均方误差（MSE）损失

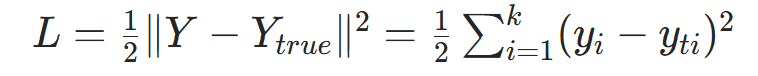
步骤 4：反向传播（Backward Propagation）

核心是链式法则：从输出层往输入层反向计算「各层误差」，再推导权重 / 偏置的梯度。反向传播的本质是 "求损失函数对每个参数的偏导数（梯度）"，梯度的物理意义是 "参数变化对损失的影响程度"。

4.1 定义 "误差项"

误差项δ：损失函数对某层「净输入Z」的偏导数（δ=∂Z∂L​），是反向传播的核心中间变量。

4.2 输出层误差项（​）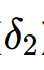

以二分类任务（Sigmoid 激活 + 二元交叉熵损失）为例：

• 第一步：损失对输出层预测值的偏导
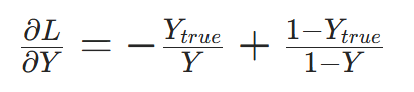
• 第二步：输出层预测值对净输入Z2的偏导（Sigmoid 导数：）
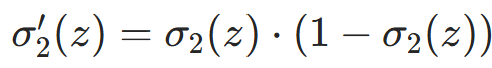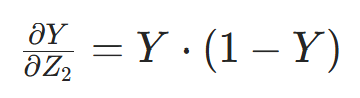
• 第三步：链式法则求输出层误差项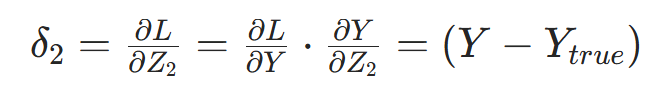结论（关键简化）：二元交叉熵 + Sigmoid 的输出层误差项可简化为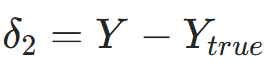，大幅降低计算量。

4.3 隐藏层误差项（​）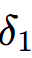

隐藏层无直接标签，需通过输出层误差反向推导：

• 第一步：损失对隐藏层输出的偏导
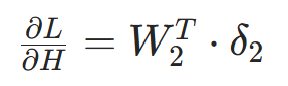
• 第二步：隐藏层输出对净输入Z1的偏导（以 ReLU 为例，导数）
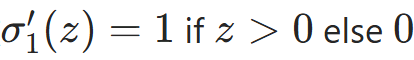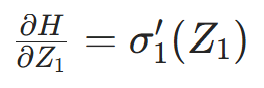
• 第三步：链式法则求隐藏层误差项

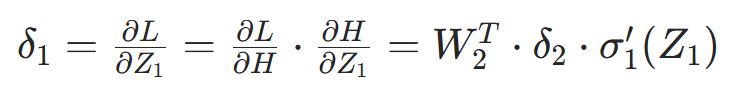
4.4 计算权重与偏置的梯度

梯度是 "损失函数对参数的偏导数"，用于后续参数更新：

• 隐藏层→输出层的权重梯度：
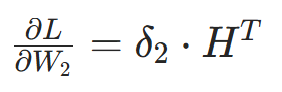
• 输出层偏置梯度（偏置的净输入导数为 1）：
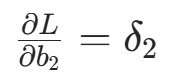
• 输入层→隐藏层的权重梯度：
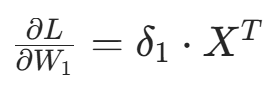
• 隐藏层偏置梯度：

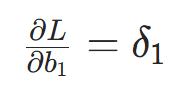
若为批量训练（样本数N），梯度需取均值：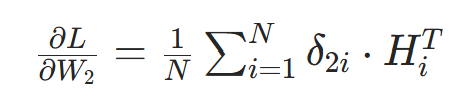

步骤 5：参数更新（梯度下降）

通过梯度下降法更新权重和偏置，核心是 "沿梯度负方向调整参数，减小损失"：

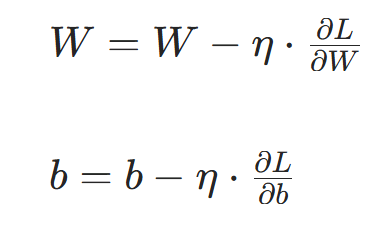
以二分类任务为例，完整更新公式：

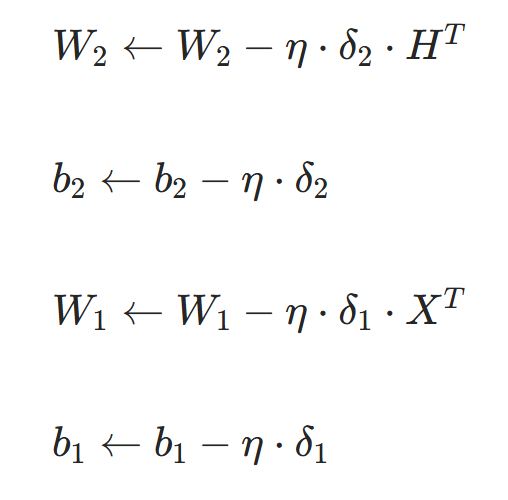
• 学习率η选择：
  • 过小：训练收敛慢，需更多迭代；
  • 过大：梯度震荡，无法收敛；
  • 常用值：0.001、0.01、0.1（小数据建议η=0.01）；
  • 优化策略：可使用「学习率衰减」（如每 10 轮迭代学习率减半）或「自适应优化器」（Adam、RMSprop）。

步骤 6：迭代训练与终止条件

重复步骤 2~5，遍历训练集进行多轮迭代，直到满足终止条件：

1. 损失函数收敛（如相邻两轮损失的差值<10−6）；
2. 达到最大迭代次数（如 epochs=20、50）；
3. 验证集准确率达到阈值（如测试集准确率>95%）。

四、BP 神经网络的Python代码完整实现

import numpy as np


# ======================== 1. 激活函数与导数 ========================
def sigmoid(z):
    """Sigmoid激活函数"""
    return 1 / (1 + np.exp(-z))


def sigmoid_derivative(z):
    """Sigmoid导数"""
    s = sigmoid(z)
    return s * (1 - s)


def relu(z):
    """ReLU激活函数"""
    return np.maximum(0, z)


def relu_derivative(z):
    """ReLU导数"""
    return np.where(z > 0, 1, 0)


# ======================== 2. BP神经网络类 ========================
class BPNeuralNetwork:
    def __init__(self, input_dim, hidden_dim, output_dim, learning_rate=0.01):
        """
        初始化BP网络
        :param input_dim: 输入层维度（如TF-IDF特征数）
        :param hidden_dim: 隐藏层神经元数
        :param output_dim: 输出层维度（二分类=1）
        :param learning_rate: 学习率
        """
        self.input_dim = input_dim
        self.hidden_dim = hidden_dim
        self.output_dim = output_dim
        self.lr = learning_rate

        # 步骤1：初始化权重和偏置
        self.W1 = np.random.normal(0, 0.01, (hidden_dim, input_dim))  # (m, n)
        self.b1 = np.zeros((hidden_dim, 1))  # (m, 1)
        self.W2 = np.random.normal(0, 0.01, (output_dim, hidden_dim))  # (k, m)
        self.b2 = np.zeros((output_dim, 1))  # (k, 1)

    def forward(self, X):
        """
        前向传播
        :param X: 输入向量 (input_dim, 1)
        :return: 隐藏层输出H、输出层预测Y
        """
        # 隐藏层计算
        Z1 = np.dot(self.W1, X) + self.b1  # (m, 1)
        H = relu(Z1)  # 隐藏层用ReLU激活 (m, 1)
        # 输出层计算
        Z2 = np.dot(self.W2, H) + self.b2  # (k, 1)
        Y = sigmoid(Z2)  # 输出层用Sigmoid激活 (k, 1)
        return H, Y

    def backward(self, X, H, Y, Y_true):
        """
        反向传播：计算梯度
        :param X: 输入向量 (input_dim, 1)
        :param H: 隐藏层输出 (hidden_dim, 1)
        :param Y: 输出层预测 (output_dim, 1)
        :param Y_true: 真实标签 (output_dim, 1)
        :return: 各参数的梯度
        """
        # 步骤4.2：输出层误差项（二元交叉熵+Sigmoid简化版）
        delta2 = Y - Y_true  # (k, 1)
        # 步骤4.3：隐藏层误差项（ReLU导数）
        Z1 = np.dot(self.W1, X) + self.b1  # 重新计算Z1（反向传播需要）
        delta1 = np.dot(self.W2.T, delta2) * relu_derivative(Z1)  # (m, 1)

        # 步骤4.4：计算梯度
        dW2 = np.dot(delta2, H.T)  # (k, m)
        db2 = delta2  # (k, 1)
        dW1 = np.dot(delta1, X.T)  # (m, n)
        db1 = delta1  # (m, 1)

        return dW1, db1, dW2, db2

    def update_params(self, dW1, db1, dW2, db2):
        """
        步骤5：参数更新（梯度下降）
        """
        self.W1 -= self.lr * dW1
        self.b1 -= self.lr * db1
        self.W2 -= self.lr * dW2
        self.b2 -= self.lr * db2

    def train(self, X_train, y_train, epochs=20, batch_size=8):
        """
        迭代训练
        :param X_train: 训练特征 (n_samples, input_dim)
        :param y_train: 训练标签 (n_samples, 1)
        :param epochs: 迭代次数
        :param batch_size: 批量大小
        """
        n_samples = X_train.shape[0]
        for epoch in range(epochs):
            # 打乱训练集（避免顺序影响）
            indices = np.random.permutation(n_samples)
            X_shuffled = X_train[indices]
            y_shuffled = y_train[indices]

            total_loss = 0.0
            # 批量训练
            for i in range(0, n_samples, batch_size):
                batch_X = X_shuffled[i:i + batch_size]
                batch_y = y_shuffled[i:i + batch_size]

                batch_loss = 0.0
                # 遍历批量内每个样本
                for X, y_true in zip(batch_X, batch_y):
                    # 重塑为列向量（适配矩阵运算）
                    X = X.reshape(self.input_dim, 1)
                    y_true = y_true.reshape(self.output_dim, 1)

                    # 步骤2：前向传播
                    H, Y = self.forward(X)

                    # 步骤3：计算损失（二元交叉熵）
                    loss = -y_true * np.log(Y) - (1 - y_true) * np.log(1 - Y)
                    batch_loss += loss.item()

                    # 步骤4：反向传播
                    dW1, db1, dW2, db2 = self.backward(X, H, Y, y_true)

                    # 步骤5：参数更新
                    self.update_params(dW1, db1, dW2, db2)

            # 打印每轮损失
            avg_loss = batch_loss / batch_size
            print(f"Epoch {epoch + 1}/{epochs}, Average Loss: {avg_loss:.4f}")

    def predict(self, X):
        """
        预测函数
        :param X: 输入特征 (n_samples, input_dim)
        :return: 预测标签（0/1）
        """
        predictions = []
        for x in X:
            x = x.reshape(self.input_dim, 1)
            _, Y = self.forward(x)
            # 二分类阈值：0.5
            pred = 1 if Y > 0.5 else 0
            predictions.append(pred)
        return np.array(predictions)


# ======================== 3. 测试算法（适配垃圾邮件检测场景） ========================
if __name__ == "__main__":
    # 模拟小数据集（输入维度=100，样本数=49）
    X_train = np.random.normal(0, 1, (49, 100))  # 替代TF-IDF特征
    y_train = np.random.randint(0, 2, (49, 1))  # 替代垃圾邮件标签

    # 初始化BP网络
    bp_net = BPNeuralNetwork(
        input_dim=100,
        hidden_dim=32,
        output_dim=1,
        learning_rate=0.01
    )

    # 训练网络
    bp_net.train(X_train, y_train, epochs=20, batch_size=8)

    # 预测测试
    X_test = np.random.normal(0, 1, (10, 100))
    y_pred = bp_net.predict(X_test)
    print("测试集预测结果：", y_pred)

五、程序运行结果展示

Epoch 1/20, Average Loss: 0.0880
Epoch 2/20, Average Loss: 0.0850
Epoch 3/20, Average Loss: 0.0893
Epoch 4/20, Average Loss: 0.0842
Epoch 5/20, Average Loss: 0.0826
Epoch 6/20, Average Loss: 0.0905
Epoch 7/20, Average Loss: 0.0904
Epoch 8/20, Average Loss: 0.0898
Epoch 9/20, Average Loss: 0.0764
Epoch 10/20, Average Loss: 0.0895
Epoch 11/20, Average Loss: 0.0762
Epoch 12/20, Average Loss: 0.0721
Epoch 13/20, Average Loss: 0.0782
Epoch 14/20, Average Loss: 0.0625
Epoch 15/20, Average Loss: 0.0750
Epoch 16/20, Average Loss: 0.0523
Epoch 17/20, Average Loss: 0.0637
Epoch 18/20, Average Loss: 0.0317
Epoch 19/20, Average Loss: 0.0299
Epoch 20/20, Average Loss: 0.0273
测试集预测结果： [0 0 1 1 0 1 1 0 1 0]

六、总结

本文详细介绍了BP神经网络的算法原理与Python实现。BP神经网络通过前向传播计算输出，反向传播利用链式法则计算梯度，采用梯度下降法更新参数以最小化预测误差。文章系统阐述了网络初始化、前向传播、损失计算、反向传播和参数更新等核心步骤，并提供了完整的Python代码实现，包括激活函数选择、误差项计算和批量训练过程。实验结果显示，该算法在模拟数据集上训练20轮后损失显著下降，验证了BP神经网络的有效性。该实现适用于二分类任务，可通过调整激活函数和损失函数扩展至多分类和回归问题。