leetcode 840. 矩阵中的幻方 中等

3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵，其中每行，每列以及两条对角线上的各数之和都相等。

给定一个由整数组成的row x col 的 grid，其中有多少个 3 × 3 的 "幻方" 子矩阵？

注意：虽然幻方只能包含 1 到 9 的数字，但 grid 可以包含最多15的数字。

示例 1：

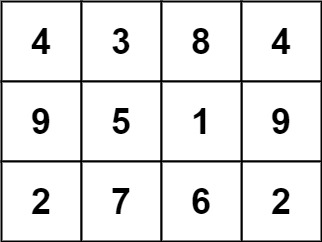
输入: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]
输出: 1
解释: 
下面的子矩阵是一个 3 x 3 的幻方：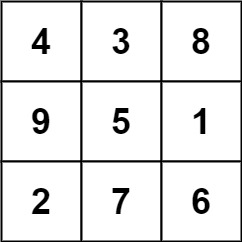

而这一个不是：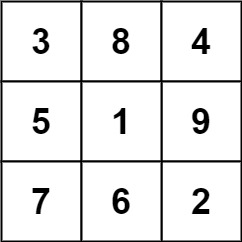

总的来说，在本示例所给定的矩阵中只有一个 3 x 3 的幻方子矩阵。

示例 2:

输入: grid = [[8]]
输出: 0

提示:

• row == grid.length
• col == grid[i].length
• 1 <= row, col <= 10
• 0 <= grid[i][j] <= 15

分析：暴力枚举每一个 3x3 子矩阵是否符合：1、每一行的和均相等；2、每一列的和均相等；3、两条斜对角线的和均相等；4、子矩阵内所有的值均落在 1,9 区间。

int numMagicSquaresInside(int** grid, int gridSize, int* gridColSize) {
    int n=gridSize,m=gridColSize[0],ans=0;
    for(int i=2;i<n;++i)
    {
        for(int j=2;j<m;++j)
        {
            int f=1,flag[20]={0};
            
            for(int a=i,k=2;k>=0;--k)
            {
                for(int b=j,l=2;l>=0;--l)
                {
                    flag[grid[a-k][b-l]]++;
                    if(flag[grid[a-k][b-l]]>1||grid[a-k][b-l]>9||grid[a-k][b-l]==0)f=0;
                }
            }

            int col_sum=grid[i][j]+grid[i][j-1]+grid[i][j-2];
            for(int k=i,t=1;t<=2&&f;++t)
            {
                int temp=grid[i-t][j]+grid[i-t][j-1]+grid[i-t][j-2];
                if(col_sum!=temp)f=0;
            }
            int row_sum=grid[i][j]+grid[i-1][j]+grid[i-2][j];
            for(int k=i,t=1;t<=2&&f;++t)
            {
                int temp=grid[i][j-t]+grid[i-1][j-t]+grid[i-2][j-t];
                if(row_sum!=temp)f=0;
            }
            int pix_sum=grid[i][j]+grid[i-1][j-1]+grid[i-2][j-2];
            int temp=grid[i][j-2]+grid[i-1][j-1]+grid[i-2][j];
            if(pix_sum!=temp)f=0;

            if(f)ans++;
        }
    }
    
    return ans;
}