经典算法题型之排序算法（四）

冒泡排序的第三种写法

第三种写法比较少见，它是在第二种写法的基础上进一步优化：

复制代码

public static void bubbleSort(int[] arr) {
    boolean swapped = true;
    // 最后一个没有经过排序的元素的下标
    int indexOfLastUnsortedElement = arr.length - 1;
    // 上次发生交换的位置
    int swappedIndex = -1;
    while (swapped) {
        swapped = false;
        for (int i = 0; i < indexOfLastUnsortedElement; i++) {
            if (arr[i] > arr[i + 1]) {
                // 如果左边的数大于右边的数，则交换，保证右边的数字最大
                int temp = arr[i];
                arr[i] = arr[i + 1];
                arr[i + 1] = temp;
                // 表示发生了交换
                swapped = true;
                // 更新交换的位置
                swappedIndex = i;
            }
        }
        // 最后一个没有经过排序的元素的下标就是最后一次发生交换的位置
        indexOfLastUnsortedElement = swappedIndex;
    }
}

经过再一次的优化，代码看起来就稍微有点复杂了。最外层的 while 循环每经过一轮，剩余数字中的最大值仍然是被移动到当前轮次的最后一位。

在下一轮比较时，只需比较到上一轮比较中，最后一次发生交换的位置即可。因为后面的所有元素都没有发生过交换，必然已经有序了。

当一轮比较中从头到尾都没有发生过交换，则表示整个列表已经有序，排序完成。

测试：

复制代码

public void test() {
    int[] arr = new int[]{6, 2, 1, 3, 5, 4};
    bubbleSort(arr);
    // 输出: [1, 2, 3, 4, 5, 6]
    System.out.println(Arrays.toString(arr));
}

冒泡排序从 1956 年就有人开始研究，之后经历过多次优化。它的空间复杂度为 O(1)，时间复杂度为 O(n^2)，第二种、第三种冒泡排序由于经过优化，最好的情况下只需要 O(n) 的时间复杂度。

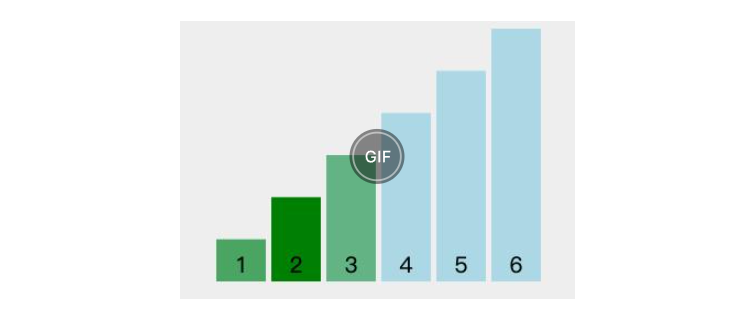
最好情况：在数组已经有序的情况下，只需遍历一次，由于没有发生交换，排序结束。

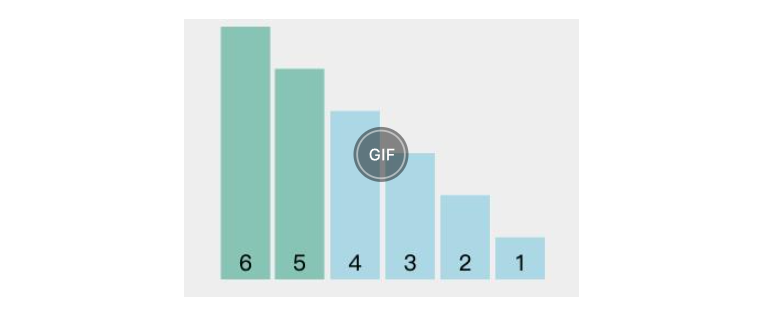
最差情况：数组顺序为逆序，每次比较都会发生交换。

但优化后的冒泡排序平均时间复杂度仍然是 O(n^2)，所以这些优化对算法的性能并没有质的提升。正如 Donald E. Knuth（1974 年图灵奖获得者）所言："冒泡排序法除了它迷人的名字和导致了某些有趣的理论问题这一事实外，似乎没有什么值得推荐的。"

不管怎么说，冒泡排序法是所有排序算法的老祖宗，如同程序界经典的 "Hello, world" 一般经久不衰，总是出现在各类算法书刊的首个章节。但面试时如果你说你只会冒泡排序可就太掉价了，接下来我们就来认识一下他的继承者们。