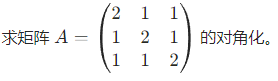一、矩阵对角化的严格定义
1. 定义
设 A 为 n 阶方阵，若存在 可逆矩阵 P 和 对角矩阵 Λ （主对角线元素为特征值，其余元素为 0），使得：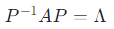
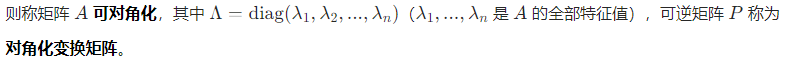
2. 核心本质
矩阵可对角化的本质是：A 能找到 n 个线性无关的特征向量（即 A 的特征向量能构成 n 维向量空间的一组基）
二、矩阵可对角化的充要条件（核心定理）
1. 充要条件 1（通用定理）
n 阶方阵 A 可对角化 当且仅当 A 有 n 个线性无关的特征向量。
证明（必要性 + 充分性）
2. 充要条件 2（重特征值判定）
n 阶方阵 A 可对角化 当且仅当 对 A 的每个 k 重特征值 λ0，其对应的特征子空间维数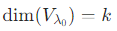 
（即 "特征值的重数 = 特征子空间维数"，也称 "特征值半单"）。
通俗理解
每个重特征值都能 "贡献" 与其重数相等的线性无关特征向量，最终所有特征向量总数为 n。
3. 充分条件（常用判定）
若 n 阶方阵 A 有 n 个 互不相同的特征值，则 A 必可对角化。
推导
由 "不同特征值的特征向量线性无关" 可知，若 A 有 n 个互不相同的特征值，则对应 n 个线性无关的特征向量，满足充要条件 1，故可对角化。
4. 特殊矩阵的对角化性质
- 实对称矩阵 ：必可对角化，且存在 正交矩阵
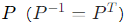，使得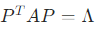
（正交对角化）。原因：实对称矩阵的特征值全为实数，且不同特征值的特征向量正交，重特征值的特征子空间维数 = 重数。
三、矩阵对角化的求解步骤（通用流程）
以 n 阶方阵 A 为例，步骤如下：
四、示例（含可对角化与不可对角化情况）
示例 1：可对角化（3 阶矩阵，含重特征值）
