leetcode1593拆分字符串使唯一子字符串数目最大

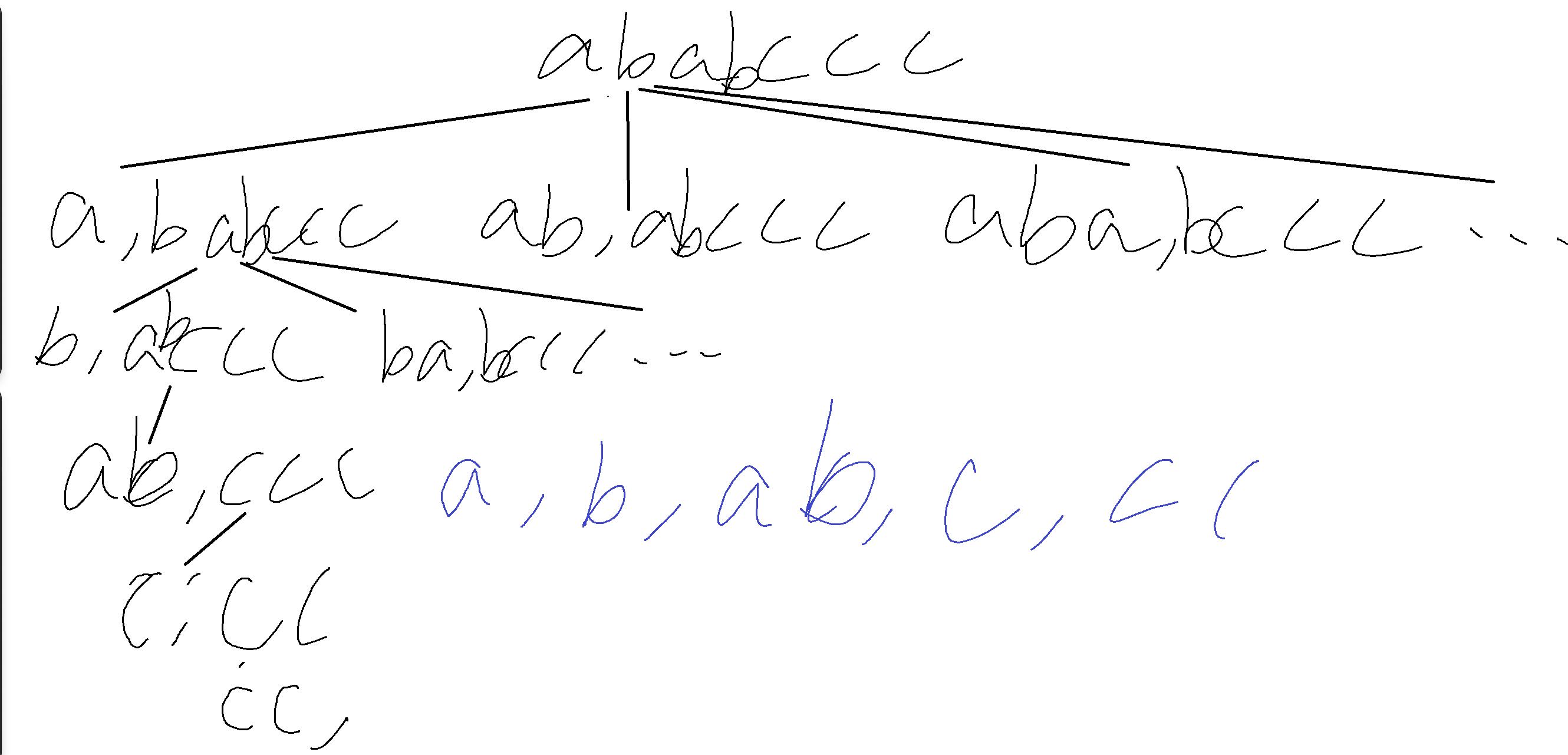
这题其实是隐式的树状结构，以ababccc为例。

以树的最左分支为例，第一刀切在下标为1的位置得 $a, babccc$ ，第二刀切在下标为2的位置得 $a, b, abccc$ , 第三刀切在下标为3的位置得 $a, b, a, bccc$ ，存在相同字符串不符合要求，第三刀重新尝试下标为4的位置得 $a, b, ab, ccc$ , 第四刀切在下标为5的位置得 $a, b, ab, c, cc$ , 第五刀切在下标为6的位置得 $a, b, ab, c, c, c$ ，存在相同字符串不符合要求，第五刀重新尝试下标为7的位置得最终结果 $a, b, ab, c, cc$

实际上，我们要求的结果就是从第二层到叶子结点的最大路径，而且树是需要通过回溯得到才能得到的。

从上面的分析中，我们能知道需要维护一个状态，中间结果subStrSet集合，并且需要一个全局变量来记录走过得所有路径的最大长度。

递归函数作用：从index下标位置开始，切完剩下的每一刀，得到最终结果，并更新全局变量。至于状态subStrSet集合，调用之前是空的，调用之后还是空的。

递归出口：index == length

状态撤销（回溯）：当前这一刀在 i 位置切完，得到 $index, i$ 子串，递归完成后面的每一刀以后，这种方案（这条路径）就完成了。那么在尝试当前这一刀在i+1的位置下刀之前，之前在 i 位置下刀得到的 $index, i$ 子串需要从subStrSet集合中移除。

java 复制代码

class Solution {
    public int maxUniqueSplit(String s) {
        //全局变量count，用来记录遍历过的路径的最大长度
        int[] count = new int[1];
        //状态subStrSet，用来记录切出的中间结果
        Set<String> subStrSet = new HashSet<>();
        //第一刀切，从下标0开始尝试
        traceBack(0, count, s, subStrSet);
        //返回最大路径长度
        return count[0];
    }
    /**
     *递归函数作用：从index下标位置开始，切完剩下的每一刀，得到最终结果。
     *并更新全局变量
     */
    private void traceBack(int index, int[] count, String s, Set<String> subStrSet){
        //如果下刀的位置到了字符串后面，说明已经完成了当前方案（路径）
        //并且路径长度大于之前尝试过的路径的最大值
        if(index == s.length() && subStrSet.size() > count[0]){
            //更新路径最大值
            count[0] = subStrSet.size();
            //退出递归
            return;
        }
        //如果最大值大于上次下刀得到的结果集大小加上剩余字符个数
        //说明剩余的每一刀切完都不可能得到比之前的方案的结果集更大，没必要再往下切了
        if(count[0] > subStrSet.size() + s.length() - index - 1) {
            return;
        }
        //从index下标位置开始尝试当前这一刀的下刀位置
        for(int i = index; i < s.length(); i++){
            //尝试下刀
            String substr = s.substring(index, i + 1);
            //如果切出来的字符串不在前面几刀所得结果集中
            if(subStrSet.add(substr)){
                //从i + 1下标位置开始，切完剩下的每一刀，得到当前方案的最终结果
                traceBack(i + 1, count, s, subStrSet);
                //当前这一刀尝试下一个位置之前，删除当前位置下刀得到的子串
                subStrSet.remove(substr);
            }
        }
    }
}