文章目录
一、前言
相移键控(Phase Shift Keying, PSK) 类调制是数字通信系统中最常见的基带调制方式之一,其基本思想是利用载波相位集合来承载离散信息。对于入门学习而言,PSK 的优势在于理论推导相对完备,且在加性高斯白噪声(Additive White Gaussian Noise, AWGN)信道下可以得到闭式误码率表达式,因而十分适合用作"理论---仿真---现象解释"一体化的教学与工程验证案例。
在通信原理相关课程中,BPSK 与 QPSK 往往作为相干检测(coherent detection)的经典代表;而差分相移键控(DPSK)则通过差分编码与差分检测,绕开了严格载波相位同步的需求,但通常会带来一定性能损失。为了在同一框架内对比三者的调制映射、接收判决方式以及误比特率(Bit Error Rate, BER)随 E b / N 0 E_b/N_0 Eb/N0 变化的规律,本文给出一套可复现的 MATLAB 仿真程序,面向 BPSK、QPSK(Gray 映射)与 2DPSK(差分二进制 PSK)在 AWGN 信道下的性能对比,并配合星座图、波形/相位示意与 BER 曲线完成直观验证。
二、程序整体功能概述
本文程序实现了一个统一的基带等效离散通信链路仿真框架,其核心由"随机比特源---PSK 映射---AWGN 加噪---接收端判决---误码统计---理论对照---图形化展示 "构成。发送端首先生成长度为 N bits N_{\text{bits}} Nbits 的二进制随机序列,并根据不同调制方式完成符号映射:BPSK 采用 0 ↦ + 1 , 1 ↦ − 1 0\mapsto +1,1\mapsto -1 0↦+1,1↦−1 的实数基带映射;QPSK 将比特按每符号两比特分组,并采用 Gray 映射将 2-bit 组合映射至四个相位点;2DPSK 则在映射前引入差分编码,使当前符号携带的是"相邻符号之间的相位变化"而非绝对相位信息。
信道部分采用 AWGN 模型。为保证不同调制方式在同一 E b / N 0 E_b/N_0 Eb/N0 下的公平比较,程序以"单位平均符号能量归一化"为基准,在此基础上由 E b / N 0 E_b/N_0 Eb/N0 推导噪声方差。对于复基带 AWGN,常用关系可写为
σ 2 = N 0 2 = E b 2 ( E b / N 0 ) = 1 2 k ⋅ ( E b / N 0 ) \sigma^2=\frac{N_0}{2}=\frac{E_b}{2(E_b/N_0)}=\frac{1}{2k\cdot (E_b/N_0)} σ2=2N0=2(Eb/N0)Eb=2k⋅(Eb/N0)1其中 k = log 2 M k=\log_2 M k=log2M 表示每个符号携带的比特数。该处理使得 BPSK ( k = 1 ) (k=1) (k=1)与 QPSK ( k = 2 ) (k=2) (k=2)在相同 E b / N 0 E_b/N_0 Eb/N0 条件下具有可比的比特能量定义,从而其 BER 曲线可以与理论结果直接对照。
接收端判决方面,BPSK 与 QPSK使用相干检测:BPSK 通过实轴零阈值判决恢复比特;QPSK 则根据接收符号相位所在象限完成符号判决,并通过 Gray 反映射恢复比特序列。对于 2DPSK,程序使用典型差分检测结构,利用相邻接收符号的共轭乘积构造判决量
z ( n ) = r ( n ) r ∗ ( n − 1 ) z(n)=r(n)r^*(n-1) z(n)=r(n)r∗(n−1)并依据 z ( n ) z(n) z(n) 的实部符号判断"相位是否翻转",从而恢复原始比特信息。最后,程序统计各个 E b / N 0 E_b/N_0 Eb/N0 点上的仿真 BER,并绘制与理论 BER 的对比曲线;同时输出多组图形,包括三类调制的理想星座图、指定信噪比下的接收星座扩散对比、BER 性能曲线以及 BPSK/2DPSK 的波形与相位示意图,以便从几何与概率两条路径解释误码行为。
三、仿真模型与关键参数设置
为了在保证统计可靠性的前提下兼顾运行效率,程序将关键参数设计为"足够大样本 + 典型信噪比扫描 + 适度可视化抽样"的组合策略。比特长度取 N bits = 2 × 10 5 N_{\text{bits}}=2\times 10^5 Nbits=2×105,使 BER 在 10 − 4 ∼ 10 − 5 10^{-4}\sim 10^{-5} 10−4∼10−5 量级仍具有一定统计意义; E b / N 0 E_b/N_0 Eb/N0扫描范围设为 0--14 dB,步长 2 dB,以覆盖从低信噪比显著扩散到高信噪比快速收敛的典型区间。星座图展示并不需要全量符号,为避免图像过密并提升可读性,程序仅抽取前 N sym,const = 3000 N_{\text{sym,const}}=3000 Nsym,const=3000 个符号用于散点展示;波形/相位示意同理,仅抽取前 N sym,wave = 50 N_{\text{sym,wave}}=50 Nsym,wave=50 个符号以呈现差分编码前后相位序列的演化特征。
调制参数方面,BPSK 与 2DPSK 均属于二进制相位集合( M = 2 M=2 M=2),每符号 1 bit( k = 1 k=1 k=1);QPSK 取 M = 4 M=4 M=4,每符号 2 bit( k = 2 k=2 k=2),并采用 Gray 映射以降低相邻符号误判导致的比特错误扩散。在能量归一化层面,QPSK 星座点通过单位平均能量处理,使 E ∣ s ∣ 2 = 1 \mathbb{E}{|s|^2}=1 E∣s∣2=1,从而与噪声方差公式中的 k k k 一致匹配;BPSK/2DPSK 映射值为 ± 1 \pm 1 ±1,同样满足单位能量条件。这一细节直接决定了"仿真曲线与理论曲线能否在同一坐标系下重合",也是 PSK 性能对比类仿真中最容易出现偏差的环节。
理论对照部分,程序给出了 BPSK 与 Gray-QPSK 在 AWGN 下的经典表达式(两者在比特误码率意义下等价):
P b = Q ( 2 E b N 0 ) = 1 2 erfc ( E b N 0 ) P_b = Q\left(\sqrt{2\frac{E_b}{N_0}}\right)=\frac{1}{2}\operatorname{erfc}\left(\sqrt{\frac{E_b}{N_0}}\right) Pb=Q(2N0Eb )=21erfc(N0Eb )
并给出 2DPSK 在差分检测条件下的理论近似:
P b 2DPSK = 1 2 exp ( − E b N 0 ) P_b^{\text{2DPSK}}=\frac{1}{2}\exp\left(-\frac{E_b}{N_0}\right) Pb2DPSK=21exp(−N0Eb)
从而在同一 BER-- E b / N 0 E_b/N_0 Eb/N0 曲线中体现"差分系统相对相干系统存在固定的性能损失"的规律。
四、关键代码片段
1、生成基带信号
matlab
% 生成随机比特序列
bits_bpsk = randi([0, 1], 1, Nbits);
bits_qpsk = randi([0, 1], 1, Nbits);
bits_dpsk = randi([0, 1], 1, Nbits);
% BPSK 调制: 0->+1, 1->-1
symbols_bpsk = 1 - 2*bits_bpsk;
% QPSK 调制 (Gray映射)
% 将比特流分组,每2比特一个符号
Nsym_qpsk = floor(Nbits/k_QPSK);
bits_qpsk_reshape = reshape(bits_qpsk(1:Nsym_qpsk*k_QPSK), k_QPSK, Nsym_qpsk);
% Gray映射表: [0,0]->0, [0,1]->1, [1,1]->2, [1,0]->3
gray_map = [0, 1, 3, 2]; % 二进制到Gray码索引
symbol_idx = bits_qpsk_reshape(1,:)*2 + bits_qpsk_reshape(2,:);
gray_idx = gray_map(symbol_idx + 1);
symbols_qpsk = exp(1j*pi/4*(2*gray_idx + 1)); % 单位能量归一化
symbols_qpsk = symbols_qpsk / sqrt(mean(abs(symbols_qpsk).^2)); % 确保单位能量
% 2DPSK 差分编码
% 差分编码: d(n) = b(n) XOR d(n-1)
diff_encoded = zeros(1, Nbits);
diff_encoded(1) = bits_dpsk(1); % 初始参考相位
for i = 2:Nbits
diff_encoded(i) = xor(bits_dpsk(i), diff_encoded(i-1));
end
% 映射到符号: 0->+1, 1->-1
symbols_dpsk = 1 - 2*diff_encoded;2、通过信道并加噪
matlab
% BPSK 加噪 (k=1, Es=Eb)
sigma_bpsk = sqrt(1/(2*EbN0_linear));
noise_bpsk = sigma_bpsk * (randn(1, Nsym_constellation) + 1j*randn(1, Nsym_constellation));
rx_bpsk = symbols_bpsk(1:Nsym_constellation) + noise_bpsk;
% QPSK 加噪 (k=2, Es=2*Eb, 归一化后Es=1)
sigma_qpsk = sqrt(1/(2*k_QPSK*EbN0_linear));
noise_qpsk = sigma_qpsk * (randn(1, Nsym_constellation) + 1j*randn(1, Nsym_constellation));
rx_qpsk = symbols_qpsk(1:Nsym_constellation) + noise_qpsk;
% 2DPSK 加噪 (k=1, Es=Eb)
sigma_dpsk = sqrt(1/(2*EbN0_linear));
noise_dpsk = sigma_dpsk * (randn(1, Nsym_constellation) + 1j*randn(1, Nsym_constellation));
rx_dpsk = symbols_dpsk(1:Nsym_constellation) + noise_dpsk;3、BER仿真循环
matlab
for idx = 1:length(EbN0_dB)
EbN0_linear = 10^(EbN0_dB(idx)/10);
%% BPSK 仿真
% 噪声方差: sigma^2 = N0/2 = Eb/(2*EbN0), 对于单位能量符号
sigma_bpsk = sqrt(1/(2*EbN0_linear));
noise_bpsk = sigma_bpsk * randn(1, Nbits); % 只需实部噪声
rx_bpsk = symbols_bpsk + noise_bpsk;
% 判决: >0 -> 0, <0 -> 1
bits_bpsk_rx = rx_bpsk < 0;
BER_bpsk_sim(idx) = sum(bits_bpsk ~= bits_bpsk_rx) / Nbits;
%% QPSK 仿真
% 噪声方差: 对于QPSK, Es=1(归一化), Eb=Es/k=1/2
% sigma^2 = N0/2 = Eb/(2*EbN0) = 1/(2*k*EbN0)
sigma_qpsk = sqrt(1/(2*k_QPSK*EbN0_linear));
noise_qpsk = sigma_qpsk * (randn(1, Nsym_qpsk) + 1j*randn(1, Nsym_qpsk));
rx_qpsk = symbols_qpsk + noise_qpsk;
% QPSK 判决 (Gray解映射)
rx_phase = angle(rx_qpsk);
rx_phase(rx_phase < 0) = rx_phase(rx_phase < 0) + 2*pi; % 转换到[0, 2*pi)
% 根据相位判决符号索引
rx_gray_idx = round((rx_phase - pi/4) / (pi/2));
rx_gray_idx = mod(rx_gray_idx, 4);
% Gray解映射
gray_demap = [0, 1, 3, 2]; % gray_idx -> symbol_idx
rx_symbol_idx = gray_demap(rx_gray_idx + 1);
% 转换回比特
bits_qpsk_rx = zeros(1, Nsym_qpsk*k_QPSK);
bits_qpsk_rx(1:2:end) = floor(rx_symbol_idx / 2);
bits_qpsk_rx(2:2:end) = mod(rx_symbol_idx, 2);
BER_qpsk_sim(idx) = sum(bits_qpsk_use ~= bits_qpsk_rx) / (Nsym_qpsk*k_QPSK);
%% 2DPSK 仿真 (差分检测)
sigma_dpsk = sqrt(1/(2*EbN0_linear));
noise_dpsk = sigma_dpsk * (randn(1, Nbits) + 1j*randn(1, Nbits));
rx_dpsk = symbols_dpsk + noise_dpsk;
% 差分检测: 计算相邻符号的相位差
% z(n) = r(n) * conj(r(n-1))
diff_detect = rx_dpsk(2:end) .* conj(rx_dpsk(1:end-1));
% 判决: real(z) > 0 -> 0 (相位不变), real(z) < 0 -> 1 (相位翻转)
bits_dpsk_rx = [bits_dpsk(1), real(diff_detect) < 0]; % 第一个比特无法恢复,用原始值
BER_dpsk_sim(idx) = sum(bits_dpsk ~= bits_dpsk_rx) / Nbits;
end五、实验仿真结果
理想星座图
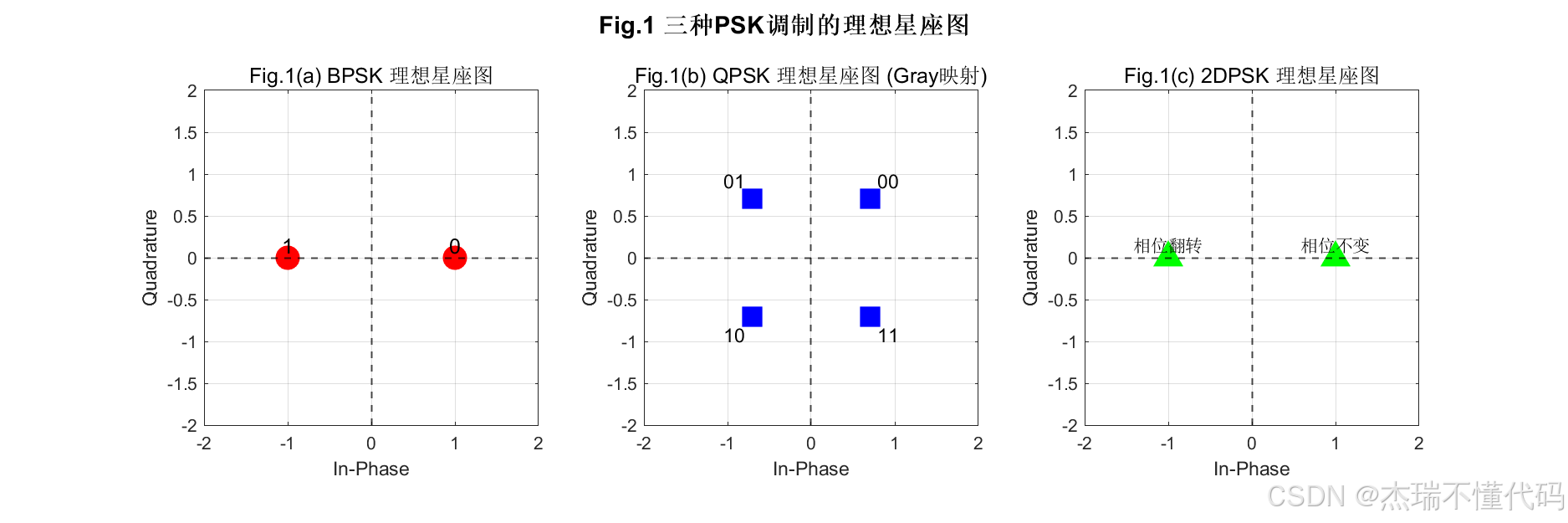
加噪后星座图对比
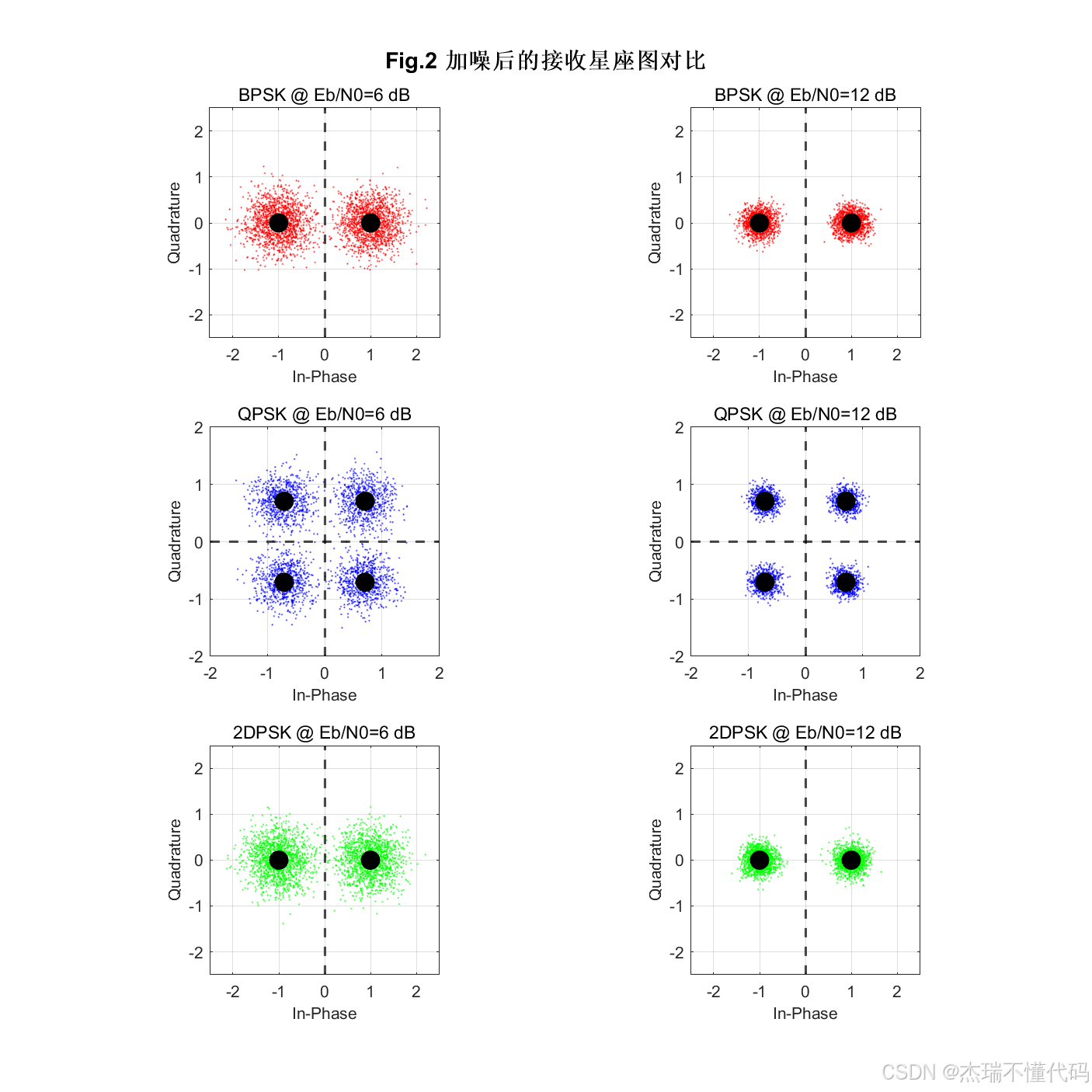
BER性能曲线对比
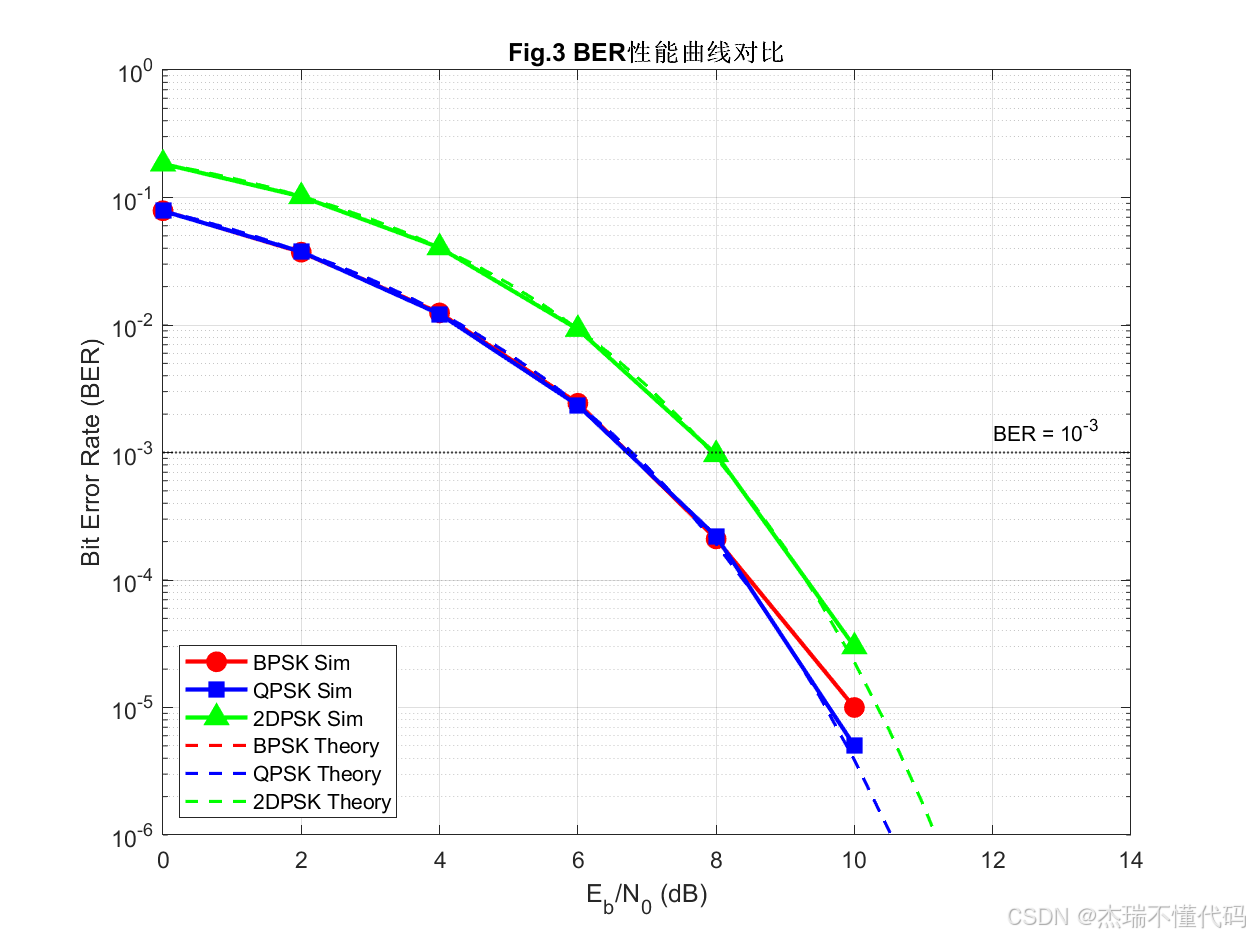
波形相位示意图
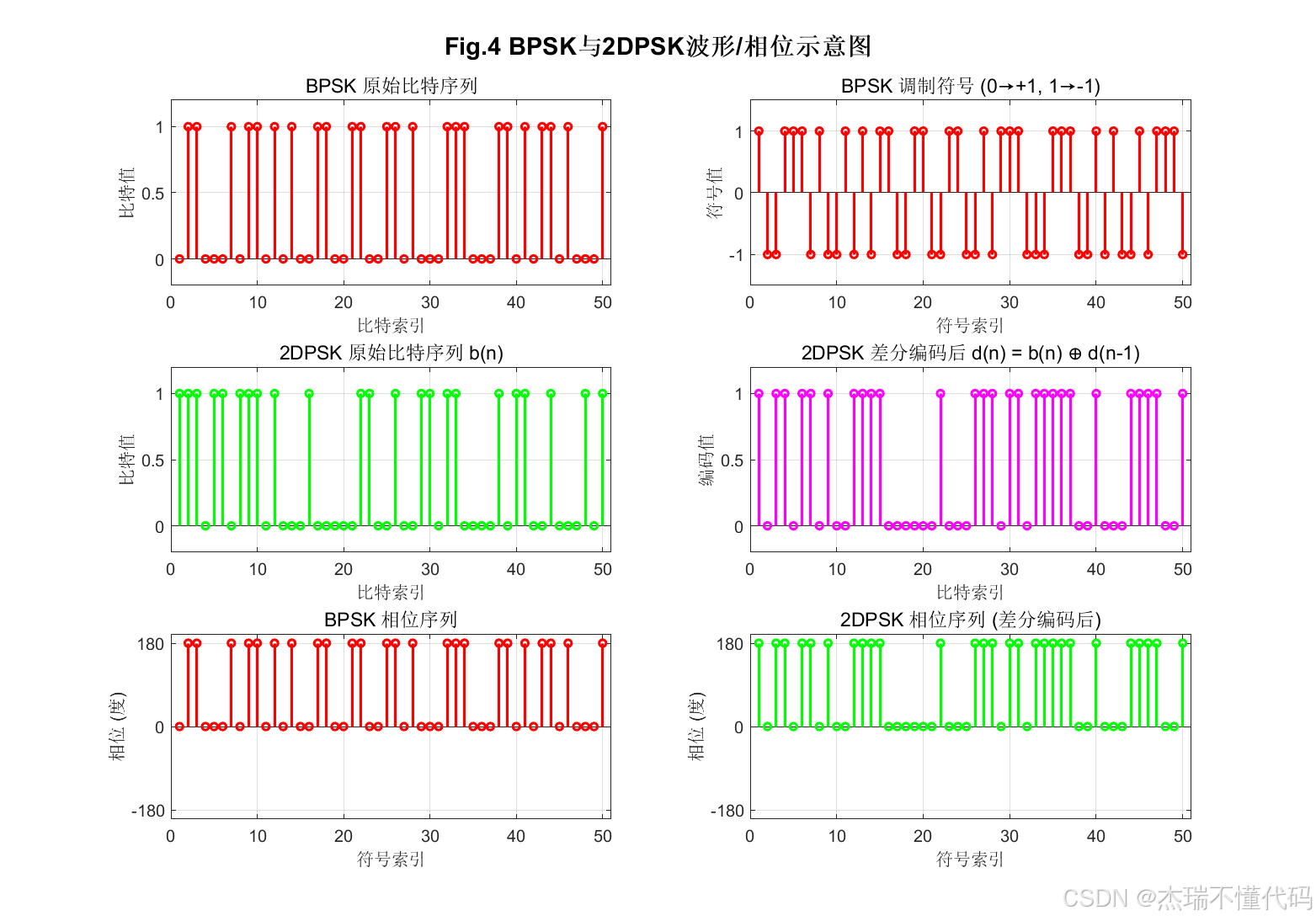
由于源代码很长,无法直接全部粘在这,因此挑了一些关键的部分予以展示,如果你对完整源码、可运行工程文件或拓展版本 感兴趣,欢迎留言交流,后续也会继续分享更多通信系统仿真相关内容,我是不懂代码的杰瑞学长,我们下期再见!
如果觉得文章对你有帮助,欢迎点赞 + 收藏 + 关注,一起进步!