欧拉角/旋转矩阵/四元素之间的转换---个人学习笔记(待完善)

爱凤的小光2026-01-03 10:06

文章目录

  • 1.欧拉角和旋转矩阵之间的转换
  • 2.欧拉角
    • [2.1 基本概念](#2.1 基本概念)
      • [2.1.1 欧拉角的名称](#2.1.1 欧拉角的名称)
      • [2.1.2 欧拉角方向](#2.1.2 欧拉角方向)
      • [2.1.3 欧拉角范围](#2.1.3 欧拉角范围)
    • [2.2 旋转顺序](#2.2 旋转顺序)
      • [2.2.1 旋转顺序和旋转轴](#2.2.1 旋转顺序和旋转轴)
      • [2.2.2 内旋和外旋](#2.2.2 内旋和外旋)
  • 3.旋转矩阵
    • [3.1 由欧拉角到旋转矩阵](#3.1 由欧拉角到旋转矩阵)
    • [3.2 任意轴旋转](#3.2 任意轴旋转)
  • 3.欧拉角与旋转矩阵相互转换
    • [3.1 欧拉角和旋转矩阵之间的转换程序示例](#3.1 欧拉角和旋转矩阵之间的转换程序示例)
  • 4.四元素
    • [4.1 欧拉角转四元素](#4.1 欧拉角转四元素)
    • [4.2 欧拉角转旋转矩阵](#4.2 欧拉角转旋转矩阵)
    • [4.3 四元数转欧拉角](#4.3 四元数转欧拉角)
    • [4.4 四元数转旋转矩阵](#4.4 四元数转旋转矩阵)
    • [4.5 旋转矩阵转四元数](#4.5 旋转矩阵转四元数)
    • [4.6 旋转矩阵转欧拉角](#4.6 旋转矩阵转欧拉角)
  • [5. 四元数、欧拉角、旋转矩阵、旋转向量之间的转换](#5. 四元数、欧拉角、旋转矩阵、旋转向量之间的转换)
    • [5.1 旋转向量](#5.1 旋转向量)
    • [5.2 旋转矩阵](#5.2 旋转矩阵)
    • [5.3 欧拉角](#5.3 欧拉角)
    • [5.4 四元数](#5.4 四元数)
  • 6.学习链接



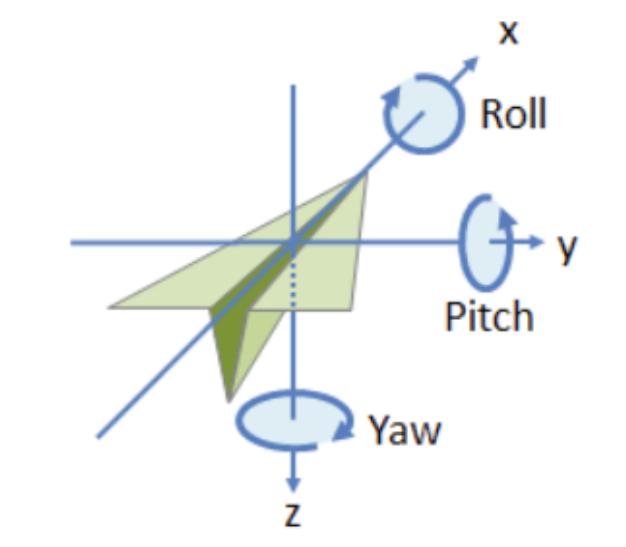
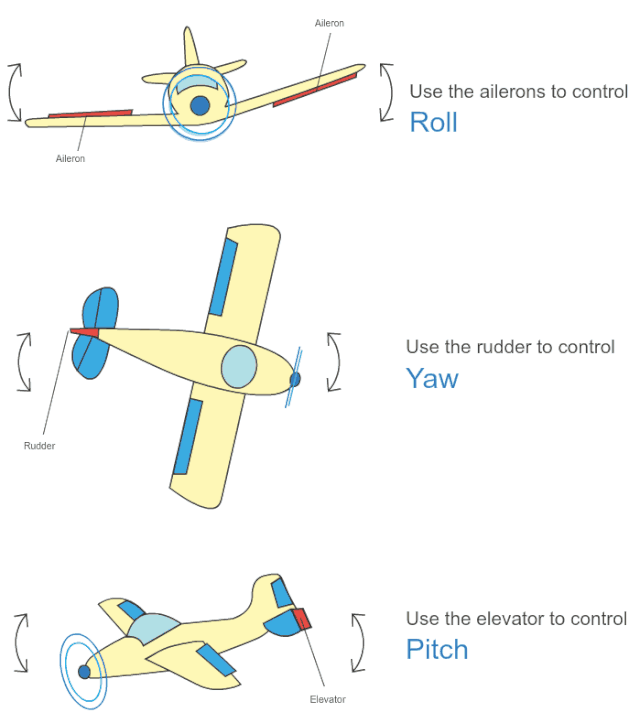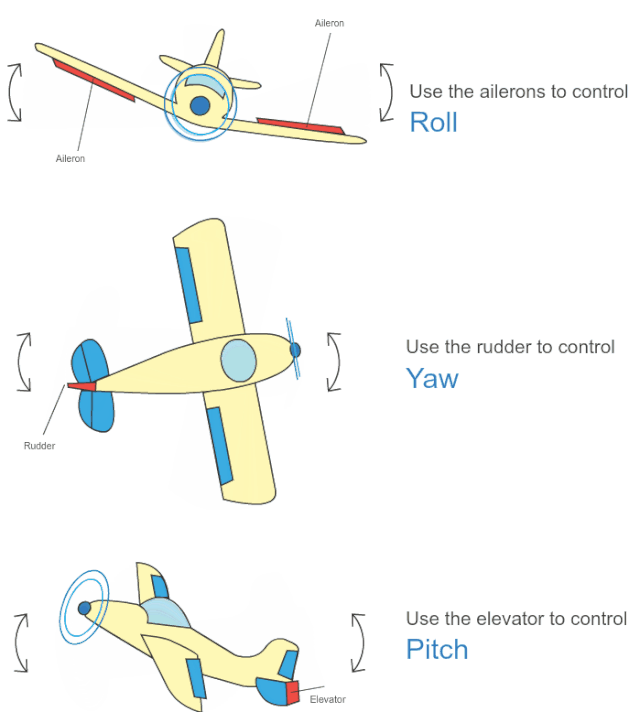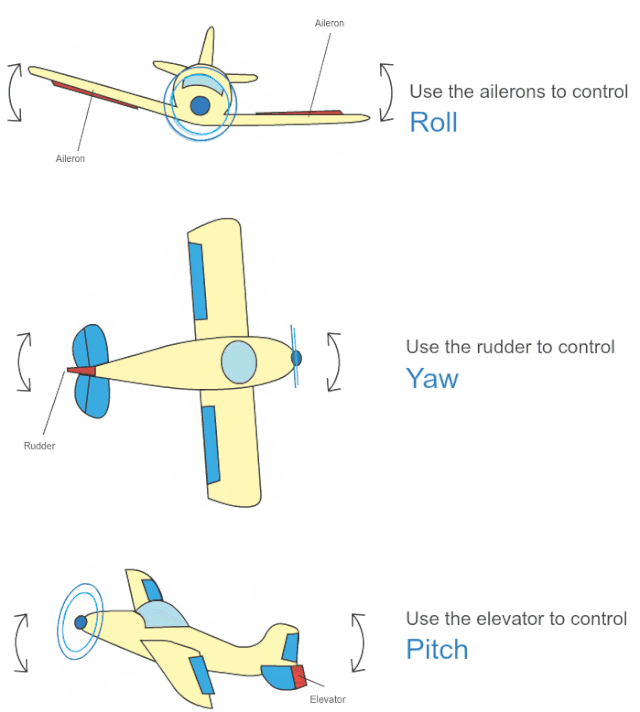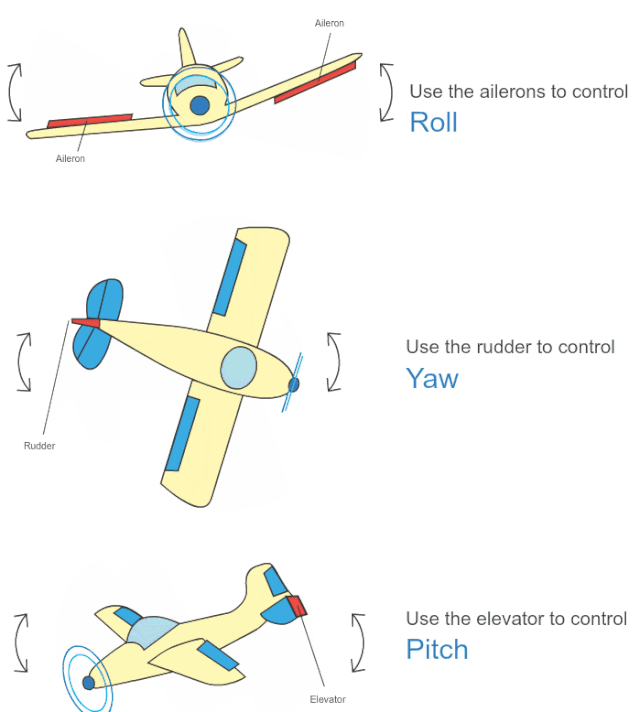
翻滚角roll是围绕x轴旋转。

俯仰角pitch是围绕y轴的旋转，可视为飞机的上下俯仰。

偏航角yaw是围绕z轴旋转，可视为控制飞机的偏航。

1.欧拉角和旋转矩阵之间的转换

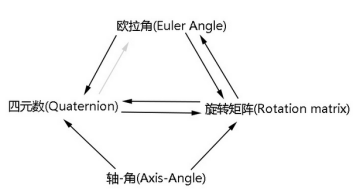
在机器人视觉应用中，经常会遇到旋转矩阵、旋转向量、四元素、欧拉角之间的相互转换。其中最容易出错的是旋转矩阵与欧拉角之间的相互转换。

2.欧拉角

2.1 基本概念

2.1.1 欧拉角的名称

1.欧拉角的叫法不固定，跟坐标轴的定义强相关。

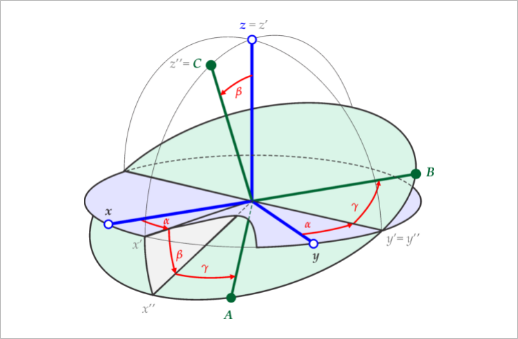
2.在图1中，假设X是车头，Y是车左方，Z是车上方，那么绕X轴旋转得到的是roll，绕Y轴旋转得到的是pitch，绕Z轴得到的是yaw。

3.在图1中，假设Y是车头，X是车右方，Z是车上方，那么绕X轴旋转得到的是pitch，绕Y轴旋转得到的是roll，绕Z轴得到的是yaw。

2.1.2 欧拉角方向

1.如果是右手系，旋转轴正方向面对观察者时，逆时针方向的旋转是正、顺时针方向的旋转是负。

2.亦可这样描述：使用右手的大拇指指向旋转轴正方向，其他4个手指在握拳过程中的指向便是正方向。

3.如图1中的三次旋转都是正向旋转。

2.1.3 欧拉角范围

1.这个要具体问题具体对待。

2.假如是车体坐标系(x-前，y-左，z-上），那么roll和pitch应该定义在（-90°，+90°），yaw应该定义在（-180°，+180°）。

3.假如是飞机坐标系，那么roll、pitch和yaw都应该定义在（-180°，+180°）。

4.Eigen 中的默认范围roll、pitch和yaw都是（-180°，+180°)。

2.2 旋转顺序

欧拉角旋转序列(Euler Angle Rotational Sequence)一共有12种顺规，6种绕三条轴的旋转(也叫Tait-Bryan Angle，XYZ,XZY,YXZ,YZX,ZXY,ZYX)，另外6种只绕两条轴的旋转(也叫Proper Euler Angle，XYX,YXY,XZX,ZXZ,YZY,ZYZ)。

2.2.1 旋转顺序和旋转轴

1.对于x,y,z三个轴的不同旋转顺序一共有(x-y-z,y-z-x,z-x-y,x-z-y,z-y-x,y-x-z)六种组合，在旋转相同的角度的情况下不同的旋转顺序得到的姿态是不一样的。

2.比如，先绕x轴旋转alpha，再绕y轴旋转beta；先绕y轴旋转beta，再绕x轴旋转alpha。这两种顺序得到的姿态是不一样的。

2.2.2 内旋和外旋

1.每次旋转是绕固定轴（一个固定参考系，比如世界坐标系）旋转，称为外旋。

2.每次旋转是绕自身旋转之后的轴旋转，称为内旋。
下图说明了内旋和外旋的区别


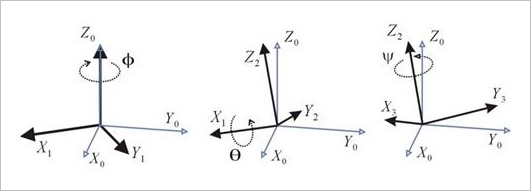
内在旋转


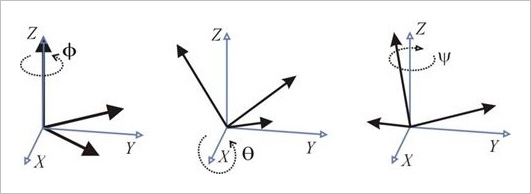
外在旋转

3.旋转矩阵

3.1 由欧拉角到旋转矩阵

假设绕XYZ三个轴旋转的角度分别为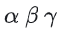 ，则三次旋转的旋转矩阵计算方法如下：

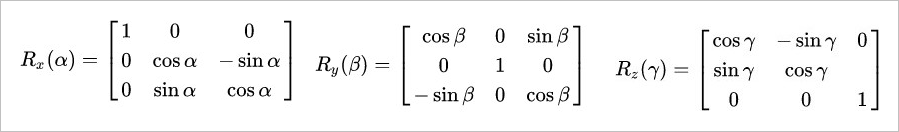
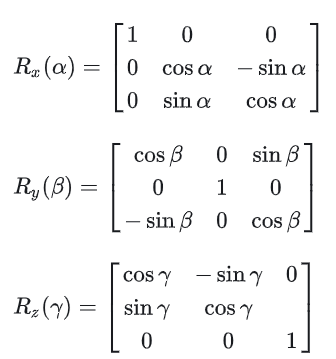
按照内旋方式，Z-Y-X旋转顺序(指先绕自身轴Z，再绕自身轴Y，最后绕自身轴X)，可得旋转矩阵(内旋是右乘)：

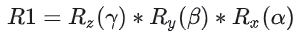
按照外旋方式，X-Y-Z旋转顺序（指先绕固定轴X，再绕固定轴Y，最后绕固定轴Z），可得旋转矩阵(外旋是左乘)：

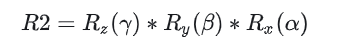
注意：这个结论说明ZYX顺序的内旋等价于XYZ顺序的外旋。

1.slam十四讲中提到的常用旋转顺序是Z-Y-X，对应rpy，指的就是内旋(绕自身轴)，Z-Y-X顺序。

2.而欧拉角转成旋转矩阵(相对于世界坐标系的旋转矩阵)，通常是按外旋方式(绕固定轴)，即X-Y-Z顺序

3.2 任意轴旋转



旋转角与旋转矩阵

3.欧拉角与旋转矩阵相互转换

以下代码用来实现旋转矩阵和欧拉角之间的相互变换。

C++语言：

cpp 复制代码 
Mat eulerAnglesToRotationMatrix(Vec3f &theta)
{
    // Calculate rotation about x axis
    Mat R_x = (Mat_<double>(3,3) <<
        1,       0,              0,
        0,       cos(theta[0]),   -sin(theta[0]),
        0,       sin(theta[0]),   cos(theta[0])
    );
    // Calculate rotation about y axis
    Mat R_y = (Mat_<double>(3,3) <<
        cos(theta[1]),    0,      sin(theta[1]),
        0,               1,      0,
        -sin(theta[1]),   0,      cos(theta[1])
    );
    // Calculate rotation about z axis
    Mat R_z = (Mat_<double>(3,3) <<
        cos(theta[2]),    -sin(theta[2]),      0,
        sin(theta[2]),    cos(theta[2]),       0,
        0,               0,                  1
    );
    // Combined rotation matrix
    Mat R = R_z * R_y * R_x;
    return R;
}
Vec3f rotationMatrixToEulerAngles(Mat &R)
{
    float sy = sqrt(R.at<double>(0,0) * R.at<double>(0,0) +  R.at<double>(1,0) * R.at<double>(1,0) );
    bool singular = sy < 1e-6; // If
    float x, y, z;
    if (!singular)
    {
        x = atan2(R.at<double>(2,1) , R.at<double>(2,2));
        y = atan2(-R.at<double>(2,0), sy);
        z = atan2(R.at<double>(1,0), R.at<double>(0,0));
    }
    else
    {
        x = atan2(-R.at<double>(1,2), R.at<double>(1,1));
        y = atan2(-R.at<double>(2,0), sy);
        z = 0;
    }
    #if 1
    x = x*180.0f/3.141592653589793f;
    y = y*180.0f/3.141592653589793f;
    z = z*180.0f/3.141592653589793f;
    #endif
    return Vec3f(x, y, z);
}

Python语言实现：

python 复制代码 
def rotationMatrixToEulerAngles(rvecs):
    R = np.zeros((3, 3), dtype=np.float64)
    cv2.Rodrigues(rvecs, R)
    sy = math.sqrt(R[0,0] * R[0,0] +  R[1,0] * R[1,0])
    singular = sy < 1e-6
    if  not singular:
        x = math.atan2(R[2,1] , R[2,2])
        y = math.atan2(-R[2,0], sy)
        z = math.atan2(R[1,0], R[0,0])
    else :
        x = math.atan2(-R[1,2], R[1,1])
        y = math.atan2(-R[2,0], sy)
        z = 0
    #print('dst:', R)
    x = x*180.0/3.141592653589793
    y = y*180.0/3.141592653589793
    z = z*180.0/3.141592653589793
    return x,y,z
def eulerAnglesToRotationMatrix(angles1) :
    theta = np.zeros((3, 1), dtype=np.float64)
    theta[0] = angles1[0]*3.141592653589793/180.0
    theta[1] = angles1[1]*3.141592653589793/180.0
    theta[2] = angles1[2]*3.141592653589793/180.0
    R_x = np.array([[1,         0,                  0                   ],
                    [0,         math.cos(theta[0]), -math.sin(theta[0]) ],
                    [0,         math.sin(theta[0]), math.cos(theta[0])  ]
                    ])
    R_y = np.array([[math.cos(theta[1]),    0,      math.sin(theta[1])  ],
                    [0,                     1,      0                   ],
                    [-math.sin(theta[1]),   0,      math.cos(theta[1])  ]
                    ])
    R_z = np.array([[math.cos(theta[2]),    -math.sin(theta[2]),    0],
                    [math.sin(theta[2]),    math.cos(theta[2]),     0],
                    [0,                     0,                      1]
                    ])
    R = np.dot(R_z, np.dot( R_y, R_x ))
    sy = math.sqrt(R[0,0] * R[0,0] +  R[1,0] * R[1,0])
    singular = sy < 1e-6
    if  not singular:
        x = math.atan2(R[2,1] , R[2,2])
        y = math.atan2(-R[2,0], sy)
        z = math.atan2(R[1,0], R[0,0])
    else :
        x = math.atan2(-R[1,2], R[1,1])
        y = math.atan2(-R[2,0], sy)
        z = 0
    #print('dst:', R)
    x = x*180.0/3.141592653589793
    y = y*180.0/3.141592653589793
    z = z*180.0/3.141592653589793
    #rvecs = np.zeros((1, 1, 3), dtype=np.float64)
    #rvecs,_ = cv2.Rodrigues(R, rvecstmp)
    return x,y,z

3.1 欧拉角和旋转矩阵之间的转换程序示例

cpp 复制代码 
#include <iostream>
#include <Eigen/Core>
#include <Eigen/Geometry>

using namespace std;

Eigen::Matrix3d eulerAnglesToRotationMatrix(Eigen::Vector3d &theta);
bool isRotationMatirx(Eigen::Matrix3d R);
Eigen::Vector3d rotationMatrixToEulerAngles(Eigen::Matrix3d &R);

const double ARC_TO_DEG = 57.29577951308238;
const double DEG_TO_ARC = 0.0174532925199433;

int main()
{
    // 设定车体欧拉角(角度)，绕固定轴
    double roll_deg = 0.5;      // 绕X轴
    double pitch_deg = 0.8;     // 绕Y轴
    double yaw_deg = 108.5;     // 绕Z轴

    // 转化为弧度
    double roll_arc = roll_deg * DEG_TO_ARC;    // 绕X轴
    double pitch_arc = pitch_deg * DEG_TO_ARC;  // 绕Y轴
    double yaw_arc = yaw_deg * DEG_TO_ARC;      // 绕Z轴

    cout << endl;
    cout << "roll_arc = " << roll_arc << endl;
    cout << "pitch_arc = " << pitch_arc << endl;
    cout << "yaw_arc = " << yaw_arc << endl;

    // 初始化欧拉角（rpy）,对应绕x轴，绕y轴，绕z轴的旋转角度
    Eigen::Vector3d euler_angle(roll_arc, pitch_arc, yaw_arc);

    // 使用Eigen库将欧拉角转换为旋转矩阵
    Eigen::Matrix3d rotation_matrix1, rotation_matrix2;
    rotation_matrix1 = Eigen::AngleAxisd(euler_angle[2], Eigen::Vector3d::UnitZ()) *
                       Eigen::AngleAxisd(euler_angle[1], Eigen::Vector3d::UnitY()) *
                       Eigen::AngleAxisd(euler_angle[0], Eigen::Vector3d::UnitX());
    cout << "\nrotation matrix1 =\n" << rotation_matrix1 << endl << endl;

    // 使用自定义函数将欧拉角转换为旋转矩阵
    rotation_matrix2 = eulerAnglesToRotationMatrix(euler_angle);
    cout << "rotation matrix2 =\n" << rotation_matrix2 << endl << endl;

    // 使用Eigen将旋转矩阵转换为欧拉角
    Eigen::Vector3d eulerAngle1 = rotation_matrix1.eulerAngles(2,1,0); // ZYX顺序，yaw,pitch,roll
    cout << "roll_1 pitch_1 yaw_1 = " << eulerAngle1[2] << " " << eulerAngle1[1] 
         << " " << eulerAngle1[0] << endl << endl;

    // 使用自定义函数将旋转矩阵转换为欧拉角
    Eigen::Vector3d eulerAngle2 = rotationMatrixToEulerAngles(rotation_matrix1); // roll,pitch,yaw
    cout << "roll_2 pitch_2 yaw_2 = " << eulerAngle2[0] << " " << eulerAngle2[1] 
         << " " << eulerAngle2[2] << endl << endl;

    return 0;
}

Eigen::Matrix3d eulerAnglesToRotationMatrix(Eigen::Vector3d &theta)
{
    Eigen::Matrix3d R_x;    // 计算旋转矩阵的X分量
    R_x <<
            1,              0,               0,
            0,  cos(theta[0]),  -sin(theta[0]),
            0,  sin(theta[0]),   cos(theta[0]);

    Eigen::Matrix3d R_y;    // 计算旋转矩阵的Y分量
    R_y <<
            cos(theta[1]),   0, sin(theta[1]),
            0,   1,             0,
            -sin(theta[1]),  0, cos(theta[1]);

    Eigen::Matrix3d R_z;    // 计算旋转矩阵的Z分量
    R_z <<
            cos(theta[2]), -sin(theta[2]), 0,
            sin(theta[2]),  cos(theta[2]), 0,
            0,              0,             1;
    Eigen::Matrix3d R = R_z * R_y * R_x;
    return R;
}


bool isRotationMatirx(Eigen::Matrix3d R)
{
    double err=1e-6;
    Eigen::Matrix3d shouldIdenity;
    shouldIdenity=R*R.transpose();
    Eigen::Matrix3d I=Eigen::Matrix3d::Identity();
    return (shouldIdenity - I).norm() < err;
}

Eigen::Vector3d rotationMatrixToEulerAngles(Eigen::Matrix3d &R)
{
    assert(isRotationMatirx(R));
    double sy = sqrt(R(0,0) * R(0,0) + R(1,0) * R(1,0));
    bool singular = sy < 1e-6;
    double x, y, z;
    if (!singular)
    {
        x = atan2( R(2,1), R(2,2));
        y = atan2(-R(2,0), sy);
        z = atan2( R(1,0), R(0,0));
    }
    else
    {
        x = atan2(-R(1,2), R(1,1));
        y = atan2(-R(2,0), sy);
        z = 0;
    }
    return {x, y, z};
}

程序输出如下：

cpp 复制代码 
roll_arc = 0.00872665
pitch_arc = 0.0139626
yaw_arc = 1.89368

rotation matrix1 =
 -0.317274  -0.948326 0.00384548
  0.948231  -0.317177  0.0160091
-0.0139622 0.00872568   0.999864

rotation matrix2 =
 -0.317274  -0.948326 0.00384548
  0.948231  -0.317177  0.0160091
-0.0139622 0.00872568   0.999864

roll_1 pitch_1 yaw_1 = 0.00872665 0.0139626 1.89368
roll_2 pitch_2 yaw_2 = 0.00872665 0.0139626 1.89368

4.四元素

一个四元数的定义如下：

cpp 复制代码 
q=q0+q1i+q2j+q3k

一个四元数拥有一个实部和三个虚部，三个虚部之间满足如下关系。

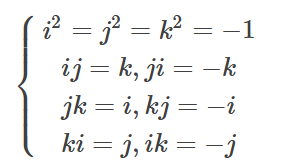
有时四元数也定义成(w,x,y,z)的形式，q0对应w，x、y、z依次对应q1、q2、q3。四元数的定义有了，那么如何用四元数表示旋转呢？如某次旋转是绕某一向量K=(Kx,Ky,Kz)进行了角度为θ的旋转，那么利用四元数就可以表示这个旋转：

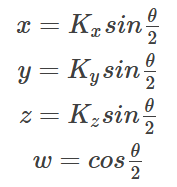
而且满足条件:

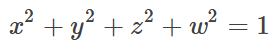
4.1 欧拉角转四元素

设ψ，θ，ϕ分别为绕Z轴、Y轴、X轴的旋转角度，对应Yaw、Pitch、Roll。

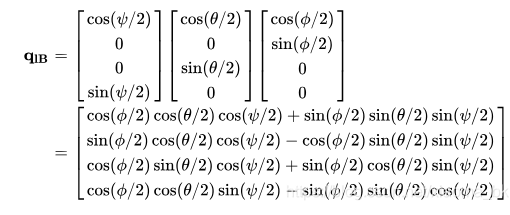
csharp 复制代码 
using System;

public class Quaternion
{
    public double W { get; set; }
    public double X { get; set; }
    public double Y { get; set; }
    public double Z { get; set; }

    public Quaternion(double w, double x, double y, double z)
    {
        W = w;
        X = x;
        Y = y;
        Z = z;
    }

    public override string ToString()
    {
        return $"Quaternion(W: {W}, X: {X}, Y: {Y}, Z: {Z})";
    }
}

public class Program
{
    public static Quaternion YDR2Quanterion(double roll, double pitch, double yaw)
    {
        // 将角度转换为弧度
        double rollRad = roll * Math.PI / 180.0;
        double pitchRad = pitch * Math.PI / 180.0;
        double yawRad = yaw * Math.PI / 180.0;

        // 计算每个轴的半角三角函数
        double cy = Math.Cos(yawRad * 0.5);
        double sy = Math.Sin(yawRad * 0.5);
        double cp = Math.Cos(pitchRad * 0.5);
        double sp = Math.Sin(pitchRad * 0.5);
        double cr = Math.Cos(rollRad * 0.5);
        double sr = Math.Sin(rollRad * 0.5);

        // 计算四元数分量
        double w = cr * cp * cy + sr * sp * sy;
        double x = sr * cp * cy - cr * sp * sy;
        double y = cr * sp * cy + sr * cp * sy;
        double z = cr * cp * sy - sr * sp * cy;

        return new Quaternion(w, x, y, z);
    }

    public static void Main(string[] args)
    {
        double roll = 30.0;  // 你可以修改这里的值来测试
        double pitch = 45.0;
        double yaw = 60.0;

        Quaternion result = YDR2Quanterion(roll, pitch, yaw);
        Console.WriteLine(result);
    }
}
cpp 复制代码 
Eigen::Quaterniond quaternion;
 
// 依次旋转yaw, pitch, roll
// 即： R = R_z * R_y * R_x
quaternion = Eigen::AngleAxisd(yaw,   Eigen::Vector3d::UnitZ()) *
             Eigen::AngleAxisd(pitch, Eigen::Vector3d::UnitY()) *
             Eigen::AngleAxisd(roll,  Eigen::Vector3d::UnitX());

而C++相关接口：

cpp 复制代码 
	Eigen::AngleAxisd yawAngle(yaw, Eigen::Vector3d::UnitZ());
	Eigen::AngleAxisd pitchAngle(pitch, Eigen::Vector3d::UnitY());
	Eigen::AngleAxisd rollAngle(roll, Eigen::Vector3d::UnitX());
	Eigen::Quaternion<double> q = yawAngle * pitchAngle * rollAngle;

4.2 欧拉角转旋转矩阵

将Z-Y-X欧拉角（或RPY角：绕固定坐标系的X-Y-Z依次旋转α, β, γ角）转换为矩阵：

cpp 复制代码 
// 先转四元数, 再转旋转矩阵
 
 
// 依次旋转yaw, pitch, roll
// 即： R = R_z * R_y * R_x
Eigen::Quaterniond quaternion = Eigen::AngleAxisd(yaw,   Eigen::Vector3d::UnitZ())*
                                Eigen::AngleAxisd(pitch, Eigen::Vector3d::UnitY())*
                                Eigen::AngleAxisd(roll,  Eigen::Vector3d::UnitX());
 
Eigen::Matrix3d rot = quaternion.toRotationMatrix();
cpp 复制代码 
Eigen::AngleAxisd yawAngle(yaw, Eigen::Vector3d::UnitZ());
Eigen::AngleAxisd pitchAngle(pitch, Eigen::Vector3d::UnitY());
Eigen::AngleAxisd rollAngle(roll, Eigen::Vector3d::UnitX());
Eigen::Quaternion<double> q = yawAngle * pitchAngle * rollAngle;
Eigen::Matrix3d rotationMatrix = q.matrix();

4.3 四元数转欧拉角

cpp 复制代码 
#define _USE_MATH_DEFINES
#include <cmath>
 
struct Quaternion {
    double w, x, y, z;
};
 
struct EulerAngles {
    double roll, pitch, yaw;
};
 
EulerAngles ToEulerAngles(Quaternion q) {
    EulerAngles angles;
 
    // roll (x-axis rotation)
    double sinr_cosp = 2 * (q.w * q.x + q.y * q.z);
    double cosr_cosp = 1 - 2 * (q.x * q.x + q.y * q.y);
    angles.roll = std::atan2(sinr_cosp, cosr_cosp);
 
    // pitch (y-axis rotation)
    double sinp = 2 * (q.w * q.y - q.z * q.x);
    if (std::abs(sinp) >= 1)
        angles.pitch = std::copysign(M_PI / 2, sinp);
    else
        angles.pitch = std::asin(sinp);
 
    // yaw (z-axis rotation)
    double siny_cosp = 2 * (q.w * q.z + q.x * q.y);
    double cosy_cosp = 1 - 2 * (q.y * q.y + q.z * q.z);
    angles.yaw = std::atan2(siny_cosp, cosy_cosp);
 
    return angles;
}

方式二

cpp 复制代码 
Eigen::Quaterniond qua;
 
// 按照yaw, pitch, roll的方式进行分解。即:
// euler(0) = yaw
// euler(1) = pitch
// euler(2) = roll
 
Eigen::Vector3d euler = qua.toRotationMatrix().eulerAngles(2, 1, 0);
return euler;

4.4 四元数转旋转矩阵

cpp 复制代码 
QuaternionBase<Derived>::toRotationMatrix(void) const;
 
Eigen::Quaterniond qua;
Eigen::Matrix<double, 3, 3> rot = qua.toRotationMatrix();

4.5 旋转矩阵转四元数

cpp 复制代码 
// 从旋转矩阵构造
Quaternion(const MatrixBase<Derived>& other) { *this = other; }
 
Eigen::Matrix<double, 3, 3> rot;
Eigen::Quaterniond qua(rot);

4.6 旋转矩阵转欧拉角

cpp 复制代码 
	Eigen::Vector3d R_ZYX = R.eulerAngles(2,1,0);
	std::cout << yaw, pitch, roll" << R_ZYX.transpose() *180/ M_PI << std::endl;
	// 或者
	double yaw = atan2(R(1,0),R(0,0)) * 180/ M_PI;

5. 四元数、欧拉角、旋转矩阵、旋转向量之间的转换

5.1 旋转向量

1.初始化旋转向量：旋转角为 alpha，旋转轴为 ( x , y , z ) (x,y,z)(x,y,z)

cpp 复制代码 
Eigen::AngleAxisd rotation_vector(alpha,Vector3d(x,y,z))；

2.旋转向量转旋转矩阵

cpp 复制代码 
Eigen::Matrix3d rotation_matrix;
rotation_matrix=rotation_vector.matrix();

Eigen::Matrix3d rotation_matrix;
rotation_matrix=rotation_vector.toRotationMatrix();

3.旋转向量转欧拉角(Z-Y-X内旋，即 RPY)

cpp 复制代码 
//(2,1,0)表示旋转顺序ZYX，数字越小表示优先级越高
Eigen::Vector3d eulerAngle=rotation_vector.matrix().eulerAngles(2,1,0);

4.旋转向量转四元数

cpp 复制代码 
Eigen::Quaterniond quaternion(rotation_vector);

5.2 旋转矩阵

初始化旋转矩阵

cpp 复制代码 
Eigen::Matrix3d rotation_matrix;
rotation_matrix<<x_00,x_01,x_02,x_10,x_11,x_12,x_20,x_21,x_22;

2.旋转矩阵转旋转向量

cpp 复制代码 
Eigen::AngleAxisd rotation_vector(rotation_matrix);

Eigen::AngleAxisd rotation_vector;
rotation_vector=rotation_matrix;

Eigen::AngleAxisd rotation_vector;
rotation_vector.fromRotationMatrix(rotation_matrix);

3.旋转矩阵转欧拉角(Z-Y-X内旋，即 RPY)

cpp 复制代码 
Eigen::Vector3d eulerAngle=rotation_matrix.eulerAngles(2,1,0);

4.旋转向量转四元数

cpp 复制代码 
Eigen::Quaterniond quaternion(rotation_matrix);
Eigen::Quaterniond quaternion;
quaternion=rotation_matrix;

5.3 欧拉角

1.初始化欧拉角(Z-Y-X，即RPY)

cpp 复制代码 
Eigen::Vector3d eulerAngle(yaw,pitch,roll);

2.欧拉角转旋转向量

cpp 复制代码 
Eigen::AngleAxisd rollAngle(AngleAxisd(eulerAngle(2),Vector3d::UnitX()));
Eigen::AngleAxisd pitchAngle(AngleAxisd(eulerAngle(1),Vector3d::UnitY()));
Eigen::AngleAxisd yawAngle(AngleAxisd(eulerAngle(0),Vector3d::UnitZ()));
Eigen::AngleAxisd rotation_vector;
rotation_vector=yawAngle*pitchAngle*rollAngle;

3.欧拉角转旋转矩阵

cpp 复制代码 
Eigen::AngleAxisd rollAngle(AngleAxisd(eulerAngle(2),Vector3d::UnitX()));
Eigen::AngleAxisd pitchAngle(AngleAxisd(eulerAngle(1),Vector3d::UnitY()));
Eigen::AngleAxisd yawAngle(AngleAxisd(eulerAngle(0),Vector3d::UnitZ()));
Eigen::Matrix3d rotation_matrix;

4.欧拉角转四元数

cpp 复制代码 
Eigen::AngleAxisd rollAngle(AngleAxisd(eulerAngle(2),Vector3d::UnitX()));
Eigen::AngleAxisd pitchAngle(AngleAxisd(eulerAngle(1),Vector3d::UnitY()));
Eigen::AngleAxisd yawAngle(AngleAxisd(eulerAngle(0),Vector3d::UnitZ()));
Eigen::Quaterniond quaternion;
quaternion=yawAngle*pitchAngle*rollAngle;

5.4 四元数

1.初始化四元数

cpp 复制代码 
Eigen::Quaterniond quaternion(w,x,y,z);

2.四元数转旋转向量

cpp 复制代码 
Eigen::AngleAxisd rotation_vector(quaternion);

Eigen::AngleAxisd rotation_vector;
rotation_vector=quaternion;

3.四元数转旋转矩阵

cpp 复制代码 
Eigen::Matrix3d rotation_matrix;
rotation_matrix=quaternion.matrix();

Eigen::Matrix3d rotation_matrix;
rotation_matrix=quaternion.toRotationMatrix();

4.四元数转欧拉角(Z-Y-X，即RPY)

cpp 复制代码 
// yaw pitch roll
Eigen::Vector3d eulerAngle=quaternion.matrix().eulerAngles(2,1,0);

下面代码与上面接口可得到相同结果：

cpp 复制代码 
static Eigen::Vector3d getEulerFromQuternion(const Eigen::Quaterniond& q)
{
    double roll, pitch ,yaw;

    // roll (x-axis rotation)
    double sinr_cosp = +2.0 * (q.w() * q.x() + q.y() * q.z());
    double cosr_cosp = +1.0 - 2.0 * (q.x() * q.x() + q.y() * q.y());
    roll = atan2(sinr_cosp, cosr_cosp);

    // pitch (y-axis rotation)
    double sinp = +2.0 * (q.w() * q.y() - q.z() * q.x());
    if (fabs(sinp) >= 1)
        pitch = copysign(M_PI / 2, sinp); // use 90 degrees if out of range
    else
        pitch = asin(sinp);

    // yaw (z-axis rotation)
    double siny_cosp = +2.0 * (q.w() * q.z() + q.x() * q.y());
    double cosy_cosp = +1.0 - 2.0 * (q.y() * q.y() + q.z() * q.z());
    yaw = atan2(siny_cosp, cosy_cosp); 

    Eigen::Vector3d eulers; 
    eulers << yaw, pitch, roll;
    return eulers;
}

6.学习链接

1.彻底搞懂"旋转矩阵/欧拉角/四元数"，让你体会三维旋转之美

2.欧拉角四元数在线可视化转换网站地址

3.三维在线旋转变换网址地址

4.Rotation Conversion Tool网站

5.3D数学基础

6.欧拉角、四元数、旋转矩阵推导及相互关系

7.旋转矩阵与欧拉角之间的转换

8.四元数计算器

9.四元数，旋转矩阵，轴角，欧拉角的相互转换（原理+Eigen代码实现）

10从零开始学习SLAM（三）

11.四元数、欧拉角、旋转矩阵、旋转向量之间的转换

相关推荐
朗迹 - 张伟1 天前
UE5 City Traffic Pro 交通插件学习笔记
笔记·学习·ue5
好奇龙猫1 天前
工智能学习-AI入试相关题目练习-第十次
人工智能·学习
来两个炸鸡腿1 天前
【Datawhale组队学习202601】Base-NLP task05 高级微调技术
人工智能·学习·自然语言处理
EverydayJoy^v^1 天前
RH134学习进程——九.访问网络附加存储
linux·网络·学习
GHL2842710901 天前
coze多agent学习
学习·ai编程
Engineer邓祥浩1 天前
设计模式学习(20) 23-18 中介者模式
学习·设计模式·中介者模式
观音山保我别报错1 天前
Spring Boot 项目学习内容详解(一)
spring boot·后端·学习
●VON1 天前
Flutter for OpenHarmony：基于三层 Tab 架构与数据模型解耦的 TodoList 产品化演进
学习·flutter·架构·openharmony·布局·技术
机器学习之心1 天前
集群中继无人机应急通信双层多目标协同优化部署：融合无监督学习与凸优化及启发式算法的MATLAB代码
学习·无人机·启发式算法·双层多目标协同优化
@––––––1 天前
论文学习笔记：FAST - 高效的视觉-语言-动作模型动作分词技术
笔记·学习
热门推荐
01GitHub 镜像站点02OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)03Claude Code Skills 实用使用手册04UV安装并设置国内源05struts2 XML外部实体注入漏洞复现（CVE-2025-68493）06Open Code教程（四）| 高级配置与集成07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08Linux下V2Ray安装配置指南09AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南10Antigravity AI编程工具添加和使用Skill完整教程