RNN循环神经网络,这是一类专门处理序列数据的神经网络模型。在transormer出现之前,LSTM(作为RNN的变体)很受欢迎,曾经是一代霸榜的模型。虽然现在热度明显不如以前了,但里面的一些工程思想仍值得我们学习。主流 LLM(如 GPT、Llama、Claude)的核心主干不用 RNN 类模型,但 RNN 类组件仍出现在辅助模块、特定场景模型及研究型混合架构中。例如阿里2025年NeurIPS最佳论文:Attention Gating Makes Better Foundation Models,其中的门控机制,思想就来源于LSTM。这里整理一下RNN类模型的基本内容以及工程实践,算是做一次回顾吧。
RNN循环神经网络
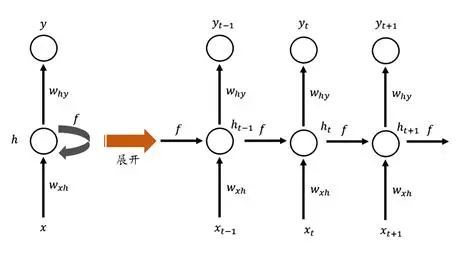
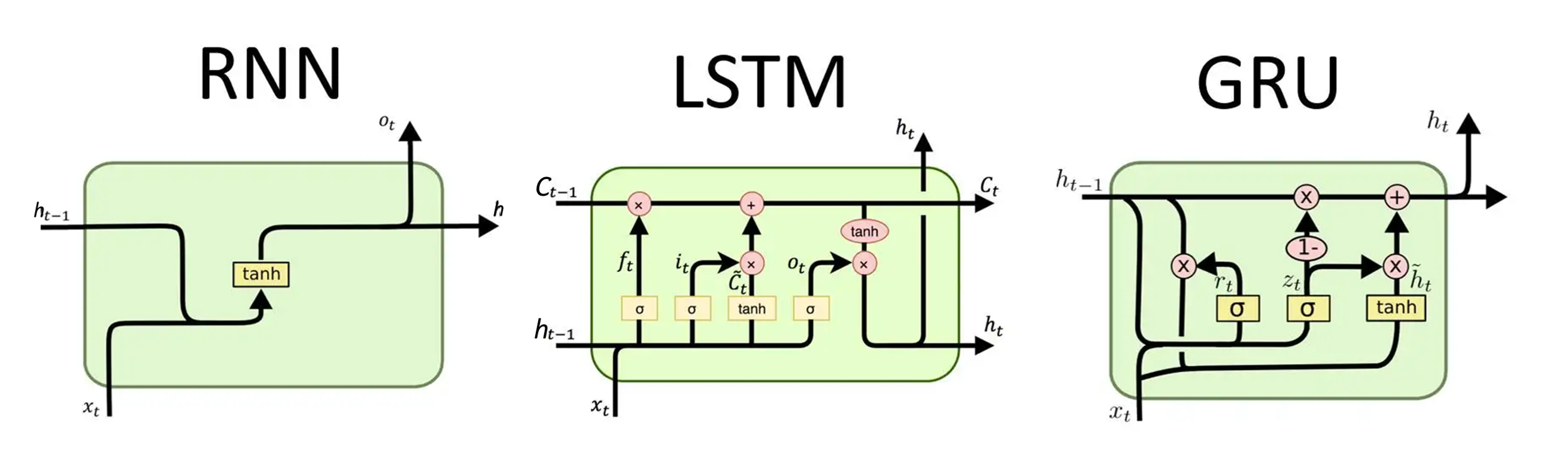
循环神经网络(Recurrent Neural Network,RNN)是一种专门处理序列数据的神经网络,它的核心特点是引入了 "记忆"------ 网络会利用之前时刻的信息来处理当前时刻的输入,这和只能处理独立样本的 CNN、全连接网络有本质区别。
-
基本思想 :RNN 通过在隐藏层增加循环连接,让隐藏状态 h t h_t ht 既依赖当前输入 x t x_t xt ,也依赖上一时刻的隐藏状态 h t − 1 h_{t-1} ht−1 。
-
核心公式 : h t = σ ( W x h x t + W h h h t − 1 + b h ) y t = σ ( W h y h t + b y ) \begin{aligned} & h_t=\sigma\left(W_{x h} x_t+W_{h h} h_{t-1}+b_h\right) \\ & y_t=\sigma\left(W_{h y} h_t+b_y\right) \end{aligned} ht=σ(Wxhxt+Whhht−1+bh)yt=σ(Whyht+by)其中 W x h , W h y , W h h W_{xh},W_{hy},W_{hh} Wxh,Why,Whh为可学习参数, b h , b y b_h,b_y bh,by为偏置项, y t y_t yt为输出。
-
优点 :天然适配序列数据、参数共享且结构灵活。
-
缺点 :梯度消失 / 爆炸------处理长序列时,早期输入的信息会逐渐丢失(梯度消失),或权重更新过大导致训练不稳定(梯度爆炸)。
-
根据输入输出的结构,RNN 可以灵活调整为不同模式,满足多样化需求:
- 一对一:类似普通神经网络(无序列特性,很少用);
- 一对多:如文本生成(输入一个关键词,输出一段文本);
- 多对一:如情感分析(输入一句话,输出一个情感标签);
- 多对多:如机器翻译、词性标注(输入输出都是序列)。
-
工程实现 :
pythonimport torch import torch.nn as nn # 1. 极简版RNN类:仅支持单层单向,聚焦核心逻辑 class SimpleRNN(nn.Module): def __init__(self, input_size, hidden_size, output_size, use_all_time_steps=False): super(SimpleRNN, self).__init__() self.hidden_size = hidden_size self.use_all_time_steps = use_all_time_steps # 控制用hn(False)还是output(True) # 仅保留基础RNN层(单层、单向、batch_first=True) self.rnn = nn.RNN(input_size, hidden_size, batch_first=True) self.fc = nn.Linear(hidden_size, output_size) def forward(self, x): # 初始化隐藏状态h0(固定单层、单向:[1, batch, hidden]) batch_size = x.size(0) h0 = torch.zeros(1, batch_size, self.hidden_size) # RNN核心前向传播:output=所有时间步状态,hn=最后时间步状态 output, hn = self.rnn(x, h0) # 二选一:用最后一步(多对一) or 所有步(多对多) if self.use_all_time_steps: out = self.fc(output) # 用output:[batch, seq_len, output_size] else: out = self.fc(hn.squeeze(0)) # 用hn:[batch, output_size] return out # 2. 测试代码:直观展示两种用法 if __name__ == "__main__": # 超参数(极简) input_size = 10 # 每个时间步特征数 hidden_size = 20 # 隐藏层维度 output_size = 5 # 输出维度 batch_size = 3 # 批次 seq_len = 8 # 序列长度 # 固定输入数据(极简:随机数仅作演示,核心看维度) x = torch.randn(batch_size, seq_len, input_size) # 测试1:多对一(用hn,不使用output) model1 = SimpleRNN(input_size, hidden_size, output_size, use_all_time_steps=False) pred1 = model1(x) print("多对一输出维度(用hn):", pred1.shape) # (3, 5) # 测试2:多对多(用output,所有时间步) model2 = SimpleRNN(input_size, hidden_size, output_size, use_all_time_steps=True) pred2 = model2(x) print("多对多输出维度(用output):", pred2.shape) # (3, 8, 5)输出结果:
多对一输出维度(用hn): torch.Size([3, 5])
多对多输出维度(用output): torch.Size([3, 8, 5])
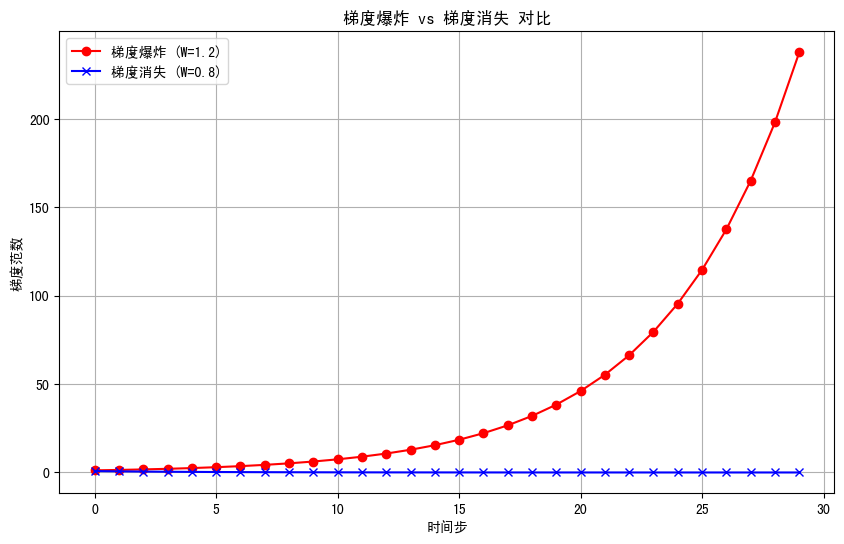
上面的代码写得很简单,只是为了简单记录一下。说到RNN,很多人点出它的梯度爆炸问题。这里简单说明一下原因:梯度计算的本质:训练 RNN 时需要通过反向传播(BPTT,时间反向传播)计算梯度,而梯度需要沿着时间步 "回溯" 计算,最终梯度会包含 W h W_h Wh的多次矩阵乘法(即 W h t W_h^t Wht)。反向传播时,关于 W h W_h Wh的梯度会表现为 W h W_h Wh的连乘形式 ∂ L ∂ W h ∝ ∑ k = 1 t W h t − k \frac{\partial L}{\partial W_h} \propto \sum_{k=1}^t W_h^{t-k} ∂Wh∂L∝∑k=1tWht−k,可以把矩阵 W h W_h Wh的特征值作为核心分析对象:
(1)梯度消失:如果W h的所有特征值的绝对值都小于 1,那么 W h t W_h^t Wht(t 次方)会随着时间步 t 增大而趋近于 0,导致梯度趋近于 0,模型无法学习长序列依赖。
(2)梯度爆炸:如果 W h W_h Wh的特征值的绝对值大于 1,那么 W h t W_h^t Wht会随着 t 增大而指数级增长,梯度变得极大,导致模型参数更新失控。
有些博客可以参考:
(2)深入理解梯度爆炸(Gradient Explosion)及解决方案
LSTM结构
LSTM 全称是 Long Short-Term Memory,中文译为长短期记忆网络,是一种专门解决循环神经网络(RNN)梯度消失 / 爆炸问题的改进型循环神经网络,由 Hochreiter & Schmidhuber 在 1997 年提出。
LSTM之父有很多梗,很有趣。
-
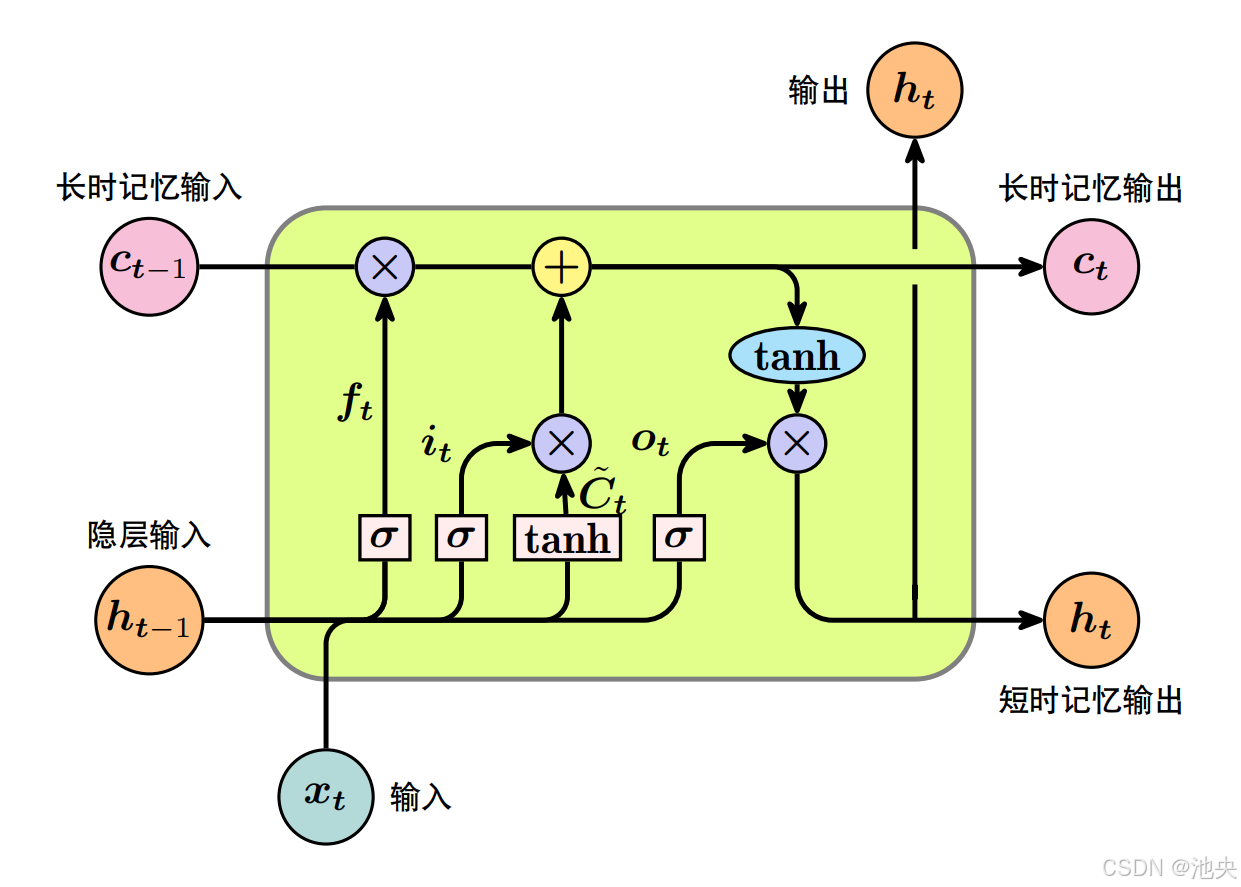
模型结构 :
-
核心公式 :围绕3 个门控单元和1个细胞状态的更新展开,所有计算都基于当前时刻输入 x t x t xt和上一时刻隐藏状态 h t − 1 h{t−1} ht−1。
- 遗忘门(Forget Gate) :决定细胞状态中需要丢弃的信息,输出值在 0~1 之间。 f t = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) f_t=\sigma\left(W_f \cdot\left[h_{t-1}, x_t\right]+b_f\right) ft=σ(Wf⋅[ht−1,xt]+bf)
- 输入门(Input Gate) ,分为两步,决定哪些新信息要存入细胞状态:
(1)筛选需要更新的信息 i t = σ ( W i ⋅ [ h t − 1 , x t ] + b i ) i_t=\sigma\left(W_i \cdot\left[h_{t-1}, x_t\right]+b_i\right) it=σ(Wi⋅[ht−1,xt]+bi)(2)生成候选的新细胞状态 C ~ t = tanh ( W C ⋅ [ h t − 1 , x t ] + b C ) \tilde{C}t=\tanh \left(W_C \cdot\left[h{t-1}, x_t\right]+b_C\right) C~t=tanh(WC⋅[ht−1,xt]+bC)- tanh 的输出值域是 [-1, 1],相比 sigmoid(值域 [0,1]),它既能输出正向信息,也能输出负向信息,这使得细胞状态可以通过加法实现 "信息增强" 或 "信息抵消",更灵活地调整状态内容。
- 此外,tanh 的导数值域是 (0, 1],在输入接近 0 时,导数接近 1,梯度衰减的速度比 sigmoid 更慢。
- 细胞状态更新 :结合遗忘门和输入门的结果,更新细胞状态 C t C_t Ct
C t = f t ⊙ C t − 1 + i t ⊙ C ~ t C_t=f_t \odot C_{t-1}+i_t \odot \tilde{C}_t Ct=ft⊙Ct−1+it⊙C~t- 细胞状态的线性更新路径,避免梯度连乘放大。这个更新过程是线性的,没有嵌套的激活函数(虽 C ~ t \tilde{C}_t C~t经过 tanh,但 C t C_t Ct本身是加法和哈达玛积的组合)。
- LSTM 细胞状态的梯度传递没有权重矩阵的连乘,只是乘以遗忘门 f t f_t ft,这就切断了梯度指数级放大的链条。
- 输出门(Output Gate) :决定当前时刻的隐藏状态输出 h t h_t ht
(1)确定输出部分的信息: o t = σ ( W o ⋅ [ h t − 1 , x t ] + b o ) o_t=\sigma\left(W_o \cdot\left[h_{t-1}, x_t\right]+b_o\right) ot=σ(Wo⋅[ht−1,xt]+bo)(2)生成最终的隐藏状态: h t = o t ⊙ tanh ( C t ) h_t=o_t \odot \tanh \left(C_t\right) ht=ot⊙tanh(Ct)
LSTM 能够缓解梯度爆炸问题,核心原因是其细胞状态的线性更新路径 和门控机制的约束作用 ,从梯度反向传播的路径上减少了梯度的指数级放大。需要注意的是,LSTM 主要缓解的是长序列带来的梯度消失问题,对梯度爆炸的缓解是辅助性的。如果权重矩阵的初始化值过大,或者训练数据分布异常,仍然可能出现梯度爆炸。此时通常需要配合梯度裁剪(Gradient Clipping) 等技巧,直接限制梯度的最大范数,来彻底解决这个问题。
-
工程实现:文本情感二分类(判断文本的情感倾向是 "正面" 还是 "负面")。这里做了简单的工程实现,仅为了说明torch内置函数的使用。
pythonimport torch import torch.nn as nn # 1. 定义极简LSTM模型(仅核心层) class SimpleLSTM(nn.Module): def __init__(self): super().__init__() self.lstm = nn.LSTM(input_size=10, hidden_size=16, batch_first=True) # 词向量10维,隐藏层16维 self.fc = nn.Linear(16, 2) # 输出2类:正面/负面 def forward(self, x): out, _ = self.lstm(x) # LSTM输出:(batch, seq_len, 16) out = out[:, -1, :] # 取最后时刻输出(整句话的情感) out = self.fc(out) # 映射到2类 return out # 2. 核心:输入定义(标注清晰) # 输入维度:[batch_size, seq_len, input_size] # 含义:2个文本样本 × 每个文本5个词 × 每个词10维向量 input_data = torch.randn(2, 5, 10) print(f"输入形状: {input_data.shape} → [2个样本, 5个词, 10维词向量]") # 3. 模型调用+输出解读 model = SimpleLSTM() output = model(input_data) # 输出维度:[batch_size, output_size] print(f"输出形状: {output.shape} → [2个样本, 2类情感概率]") print(f"输出值:\n{output}") print("\n输出解读:") for i in range(2): pos_score = torch.softmax(output[i], dim=0)[0].item() # 正面概率 neg_score = torch.softmax(output[i], dim=0)[1].item() # 负面概率 sentiment = "正面" if pos_score > neg_score else "负面" print(f"样本{i+1}:正面概率={pos_score:.2f},负面概率={neg_score:.2f} → 判定为{sentiment}") -
优点:解决长时序依赖问题;普适性强,适配多类时序任务;训练与部署成本适中。
-
缺点:参数冗余,计算成本高于简化变体;长序列处理能力仍有上限;对超参数敏感,调参成本高;
GRU结构
GRU (Gated Recurrent Unit) 是一种常用于处理序列数据的循环神经网络(RNN)变体,由 Kyunghyun Cho 等人在 2014 年提出。GRU可以看作一种简化版本的LSTM。
-
模型结构 :
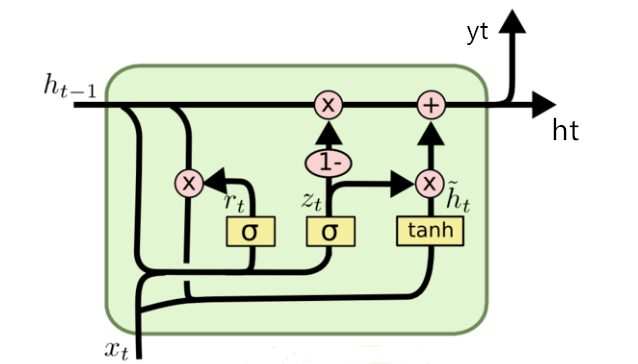
GRU 包含 2 个核心门控,通过门控的开关状态来控制信息的传递与遗忘:
- 重置门(Reset Gate, r t r_t rt):决定是否忽略上一时刻的隐藏状态信息,让模型更关注当前输入。 r t = σ ( W r ⋅ [ h t − 1 , x t ] ) r_t=\sigma\left(W_r \cdot\left[h_{t-1}, x_t\right]\right) rt=σ(Wr⋅[ht−1,xt])
- 更新门(Update Gate, z t z_t zt):同时决定保留多少上一时刻的信息和加入多少当前时刻的新信息。 z t = σ ( W z ⋅ [ h t − 1 , x t ] ) z_t=\sigma\left(W_z \cdot\left[h_{t-1}, x_t\right]\right) zt=σ(Wz⋅[ht−1,xt])
- 候选隐藏状态( h ~ t \tilde{h}_t h~t):生成当前时刻的候选状态,结合了重置门处理后的历史信息和当前输入。 h ~ t = tanh ( W h ⋅ [ r t ⊙ h t − 1 , x t ] ) \tilde{h}t=\tanh \left(W_h \cdot\left[r_t \odot h{t-1}, x_t\right]\right) h~t=tanh(Wh⋅[rt⊙ht−1,xt])
- 最终隐藏状态( h t h_t ht):由更新门调节,融合上一时刻隐藏状态和候选隐藏状态。 h t = ( 1 − z t ) ⊙ h t − 1 + z t ⊙ h ~ t h_t=\left(1-z_t\right) \odot h_{t-1}+z_t \odot \tilde{h}_t ht=(1−zt)⊙ht−1+zt⊙h~t
-
工程实现
pythonimport torch import torch.nn as nn class CustomGRU(nn.Module): def __init__(self, input_size, hidden_size, output_size): super().__init__() self.gru = nn.GRU(input_size, hidden_size, batch_first=True) self.fc = nn.Linear(hidden_size, output_size) def forward(self, x, h_0=None): # 自动初始化全0隐藏状态 if h_0 is None: h_0 = torch.zeros(1, x.size(0), self.gru.hidden_size, device=x.device) out, _ = self.gru(x, h_0) return self.fc(out) if __name__ == "__main__": input_size = 8 # 输入特征维度 hidden_size = 16 # GRU隐藏层维度 output_size = 2 # 输出维度(二分类) batch_size = 2 # 批次大小 seq_len = 5 # 序列长度 model = CustomGRU(input_size, hidden_size, output_size) x = torch.randn(batch_size, seq_len, input_size) # 输入形状 [2,5,8] output = model(x) print(f"输入形状: {x.shape}") # [2, 5, 8] print(f"GRU输出形状: {output.shape}")# [2, 5, 2] print(f"输出前2个值:\n{output[0,0,:]}") # 打印第一个样本第一个时间步的输出 -
GRU对比LSTM
对比维度 GRU(门控循环单元) LSTM(长短期记忆网络) 核心门控 2 个(重置门、更新门) 3 个(遗忘门、输入门、输出门) 状态数量 1 个(隐藏状态 h t h_t ht) 2 个(细胞状态 c t c_t ct+ 隐藏状态 h t h_t ht) 参数 / 训练速度 少、快 多、慢 长序列表现 中等 更优 适用场景 小数据、快训练、中等序列 大数据、高精度、超长序列
三种RNN结构与当前主流LLM
这里简单对比一下当前的RNN模型与主流LLM框架,如下表所示:
| 对比维度 | RNN类方法(基础RNN、LSTM、GRU) | 主流LLM框架(基于Transformer,如GPT、LLaMA、BERT) |
|---|---|---|
| 核心机制 | 循环依赖结构,逐词串行处理序列数据,隐藏状态传递上下文 | 自注意力机制,并行计算序列中所有token的关联关系,捕捉全局依赖 |
| 长序列处理能力 | 存在梯度消失/爆炸问题,LSTM/GRU仅缓解无法根治,难以处理长依赖 | 可通过注意力掩码、RoPE、FlashAttention等技术优化,支持万级以上token长序列 |
| 计算效率 | 串行计算,每一步依赖前一步结果,长序列下效率极低 | 并行计算,训练和推理效率远高于RNN,尤其在长序列任务中优势明显 |
| 模型规模与扩展性 | 参数量多为百万~千万级,受限于串行结构,扩展性差 | 参数量可达到十亿~万亿级,支持分布式训练框架(DeepSpeed、Megatron-LM),扩展性强 |
| 上下文理解能力 | 仅能捕捉单向或有限双向的局部上下文依赖 | 可灵活实现单向(如GPT)或双向(如BERT)的全局上下文理解 |
| 训练/部署成本 | 成本低,普通GPU即可完成训练,部署无需复杂优化 | 成本高,需多卡GPU/TPU集群训练,部署依赖量化、模型并行等优化技术 |
| 应用场景 | 短序列任务(如简单文本分类、短文本生成、传感器时序数据处理) | 复杂自然语言任务(如对话生成、代码编写、多模态理解、长文档摘要) |
RNN以前刚提出的时候,记忆机制也是其一大"优势"。现在LLM也有研究记忆机制的工作,对比RNN还是有很大差异:
- 机制本质 :RNN 是 "内置循环记忆" ,记忆在隐藏状态中串行流动,与计算过程不可分割;LLM 是 "混合记忆体系",短期靠上下文窗口,长期靠外部存储,记忆可灵活调度。
- 长依赖能力 :RNN 的门控只能缓解长依赖问题 ,无法彻底解决;LLM 通过自注意力直接建模全局关联,再结合 RoPE、FlashAttention 等技术,长序列处理能力远超 RNN。
- 记忆灵活性 :RNN 的记忆更新是被动覆盖 ,无显式检索与管理;LLM 可主动压缩、检索、增删记忆,支持跨会话持久化,更适配复杂任务与个性化需求。
- 计算与扩展 :RNN 串行计算 导致效率与扩展性受限;LLM 并行计算 + 分布式训练,可支撑万亿级参数量,外部记忆的引入进一步突破了容量瓶颈。
从这个角度看,RNN在LLM时代无疑是被打击到了,确实不算是主流的模型了。不过Bengio等人还是时不时做出一些改进工作,近期仍有人提出一些新的RNN变体模型,主要围绕解决传统 RNN 长序列建模弱、Transformer 二次复杂度高的痛点,以下是 2023---2025 年最具代表性的类型与模型,如下表:
| 模型 | 发布时间 | 核心创新 | 适用场景 |
|---|---|---|---|
| RWKV 系列(含 RWKV-7) | 2023---2025 | 双线性 RNN + 广义 Delta 规则,动态状态演化 + 门控精简 | 语言建模、长文本生成、多模态任务 |
| minLSTM/minGRU | 2025 | Bengio 团队提出,极简门控 + 并行扫描训练 | 大规模序列建模、低资源训练 |
| Comba | 2025 | 闭环反馈 RNN,SPLR 变换 + 块级并行 | 语言模型、视觉分类、目标跟踪 |
| DeltaNet(含 Gated DeltaNet) | 2024---2025 | 对角 + 低秩状态转移矩阵,在线梯度监督记忆更新 | 长序列依赖建模、检索任务 |
| RAT | 2025 | 块内循环 + 块间注意力,平衡效率与精度 | 大规模语言模型、长文本生成 |
| mLSTM/mLSTMsig | 2024---2025 | 线性 RNN + 改进门控,适配并行内核 | 通用序列建模、适配硬件优化 |
研究展望
-
对于复杂系统建模,RNN类神经网络还是有挺大的发展前景。比如储备池网络(算是RNN变体)可以用于混沌系统的建模[1];复杂系统临界点预测相关工作也有使用GRU作为核心模块的(效果是有可能比注意力机制模型好的)[2];RNN天然适配时序数据,做小样本数据或者短时序列的场景,可能效果优于预训练的基础模型。
-
在LLM时代,RNN 并未完全过时,而是在效率优化、长上下文处理、轻量部署与混合架构融合等方向还是展现出独特价值。这几年也有RWKV [3]等新型 RNN 为代表的架构,前景主要集中在线性推理成本、轻量场景适配、架构融合创新与时序建模刚需四大方向,同时需克服并行性与长依赖等固有局限。具体还得继续观望。
随手写的稿,更多是为了回顾一下。有问题可邮箱联系。