OpenCV(五十)：meanshift图像分割

MeanShift 算法

MeanShift（均值漂移）是一种基于密度梯度的非参数聚类算法 ，最早用于统计学中的密度估计，后来被广泛应用于图像分割、目标跟踪、特征空间聚类 等领域。在 OpenCV 中，MeanShift 主要用于图像分割和平滑（边缘保持滤波）。

与 K-Means 不同，MeanShift 不需要预先指定聚类个数，而是通过在特征空间中不断向高密度区域"漂移"，最终收敛到密度峰值点，实现自动聚类。

MeanShift 的基本思想

1. 密度估计思想

假设在特征空间中存在一组样本点，MeanShift 的目标是找到这些样本的概率密度函数的极值点（模式点）。

核心思想可以概括为一句话：

一个点应当向其邻域内样本分布最密集的方向移动

2. 均值漂移向量（Mean Shift Vector）

给定一个点 x，其均值漂移向量定义为：

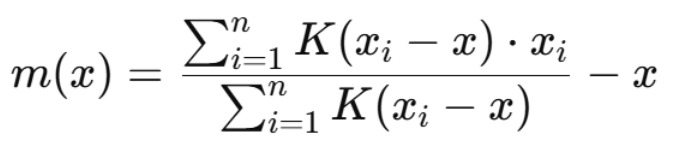
其中：

xi：样本点
K(⋅)：核函数（常用高斯核或均匀核）
m(x)：均值漂移向量

算法通过不断更新：

x←x+m(x)

直到收敛。

3. 在图像分割中的含义

在图像分割中：

每一个像素被视为一个样本点
特征向量通常为：

(x,y,R,G,B)

即 空间坐标 + 颜色特征

MeanShift 会把空间上接近、颜色上相似的像素自动聚为同一类，从而实现分割。

OpenCV 中的 MeanShift 图像分割

1. OpenCV 的实现方式

OpenCV 并未直接提供一个叫 meanShiftSegmentation() 的接口，而是通过：

pyrMeanShiftFiltering()
MeanShift + 后续区域合并

来实现图像分割效果。

常用接口：

python 复制代码

dst = cv2.pyrMeanShiftFiltering(
    src,
    sp,
    sr,
    dst=None,
    maxLevel=1,
    termcrit=None
)

2. 参数含义

参数名	类型	是否必填	默认值	含义说明	对结果的影响	推荐取值
`src`	`np.ndarray`	是	无	输入彩色图像（BGR，uint8，3 通道）	决定处理对象	必须为 BGR 彩色图
`sp`	`int / float`	是	无	空间窗口半径（Spatial Radius）	控制空间邻域大小，影响区域尺寸	10 ~ 30
`sr`	`int / float`	是	无	颜色窗口半径（Color Radius）	控制颜色相似度，影响合并程度	20 ~ 50
`dst`	`np.ndarray / None`	否	`None`	输出图像	不影响算法	通常省略
`maxLevel`	`int`	否	`1`	图像金字塔最大层数	影响速度和细节	0 ~ 2
`termcrit`	`cv2.TermCriteria`	否	`MAX_ITER+EPS, 5, 1`	迭代终止条件	影响收敛速度	一般默认

3. 金字塔 MeanShift（Pyramid MeanShift）

OpenCV 使用的是 多尺度金字塔 MeanShift：

先在低分辨率图像上进行 MeanShift
再逐层向高分辨率传播结果
提升性能，减少计算量

这使得 MeanShift 在大图像上仍具备一定实用性。

4. python示例

python 复制代码

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 1. 读取图像
img = cv2.imread("test.jpg")
if img is None:
    raise ValueError("图像读取失败，请检查路径")

# OpenCV 读入是 BGR，转 RGB 方便显示
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 2. MeanShift 参数
sp = 20   # 空间窗口半径
sr = 40   # 颜色窗口半径
max_level = 1

# 3. 执行 MeanShift 滤波（分割）
dst = cv2.pyrMeanShiftFiltering(
    img,
    sp=sp,
    sr=sr,
    maxLevel=max_level
)

dst_rgb = cv2.cvtColor(dst, cv2.COLOR_BGR2RGB)

# 4. 显示结果
plt.figure(figsize=(10, 5))

plt.subplot(1, 2, 1)
plt.title("Original Image")
plt.imshow(img_rgb)
plt.axis("off")

plt.subplot(1, 2, 2)
plt.title("MeanShift Segmentation")
plt.imshow(dst_rgb)
plt.axis("off")

plt.show()

MeanShift 分割效果特点

1. 优点

（1）无需预先指定聚类数

与 K-Means 不同，MeanShift 自动决定分割区域数量

（2）边缘保持能力强

对颜色和空间同时约束
分割区域边界自然

（3）对噪声有一定鲁棒性

基于局部密度统计，不易被孤立噪声影响

（4）结果稳定

不依赖随机初始化
多次运行结果一致

2. 缺点

（1）计算复杂度高

理论复杂度接近 O(n^2)
对高分辨率图像不友好

（2）参数敏感

sp、sr 不同，分割效果差异明显
需要经验调参

（3）不适合实时高帧率场景

在视频实时处理时性能受限

MeanShift 与其他分割算法对比

算法	是否需指定类别数	边缘保持	速度	适用场景
K-Means	是	一般	快	简单分割
MeanShift	否	强	慢	自然图像
Watershed	否	很强	中	精细边界
GraphCut	是	很强	慢	交互分割
SLIC 超像素	否	较强	快	预分割

MeanShift 更偏向于 "高质量、低实时性" 的分割需求。

总结

MeanShift 是一种经典而优雅的图像分割算法，其核心优势在于：

无需指定类别数
能在颜色与空间联合特征中进行自适应聚类
分割结果自然、边缘友好

在 OpenCV 中，pyrMeanShiftFiltering 提供了工程化实现，使其在实际项目中仍具有一定实用价值。但由于其计算复杂度较高，更适合离线图像处理、预处理阶段或对分割质量要求高的应用场景。