[机器学习-从入门到入土] 模型评估与选择

个人导航

知乎：https://www.zhihu.com/people/byzh_rc

CSDN：https://blog.csdn.net/qq_54636039

注：本文仅对所述内容做了框架性引导，具体细节可查询其余相关资料or源码

参考文章：各方资料

文章目录

[[机器学习-从入门到入土] 模型评估与选择](#[机器学习-从入门到入土] 模型评估与选择)
个人导航
[经验误差 vs 泛化误差](#经验误差 vs 泛化误差)
- - - [1.经验误差（empirical error）](#1.经验误差（empirical error）)
    - [2.泛化误差（generalization error）](#2.泛化误差（generalization error）)
过拟合与欠拟合
[测试误差与 i.i.d. 假设](#测试误差与 i.i.d. 假设)
- - - 用`测试误差`近似`泛化误差`
    - [i.i.d. 假设的作用](#i.i.d. 假设的作用)
    - 训练集与测试集必须互斥
数据集划分方法
- - - 1.留出法（Hold-out）
    - [2.交叉验证（Cross Validation）](#2.交叉验证（Cross Validation）)
    - 3.自助法（Bootstrapping）
[参数调优（Parameter Tuning）](#参数调优（Parameter Tuning）)
- - - [超参数 vs 参数](#超参数 vs 参数)
    - 为什么需要验证集validation
    - 网格搜索
[性能度量 Performance Measure](#性能度量 Performance Measure)
- - - 1.混淆矩阵
    - 2.Precision（查准率）
    - [3.Recall（召回率 / 查全率）](#3.Recall（召回率 / 查全率）)
    - [4.权衡 Precision 与 Recall](#4.权衡 Precision 与 Recall)
    - [5. F1-score（综合指标）](#5. F1-score（综合指标）)
    - [6. P-R 曲线 (Precision-Recall Curve)](#6. P-R 曲线 (Precision-Recall Curve))
    - [7. ROC 曲线 (Receiver Operating Characteristic)](#7. ROC 曲线 (Receiver Operating Characteristic))
    - 总结比较

经验误差 vs 泛化误差

1.经验误差（empirical error）

模型在训练集上的误差（训练误差）

是一个可观测量 , 不等价于模型真实能力
经验误差可以被刻意压得很低（甚至为 0）

2.泛化误差（generalization error）

模型在未见过的新样本上的误差（真实目标）

真正想最小化的量
泛化误差不可直接计算

过拟合与欠拟合

1.过拟合（Overfitting）

训练误差小，泛化误差大

把训练数据中的噪声当成了规律

2.欠拟合（Underfitting）

训练误差和泛化误差都大

模型能力不足, 连训练集的基本模式都刻画不了

过拟合无法被彻底解决

若能彻底解决过拟合，相当于证明 P = NP

P（Polynomial time）

→ 容易「找到答案」的问题

NP（Nondeterministic Polynomial time）

→ 容易「验证答案」的问题

P vs NP 问题：

是否所有"容易验证"的问题，也都"容易求解"？

测试误差与 i.i.d. 假设

用`测试误差`近似`泛化误差`

泛化误差不可计算

-> 只能用"未见样本"的误差来估计

i.i.d. 假设的作用

i.i.d. = independent and identically distributed = 独立同分布

这是整个统计学习理论的根基假设

若不满足 i.i.d., 则测试误差 ≠ 泛化误差

-> 所有评估方法都会失效

训练集与测试集必须互斥

若测试集泄漏训练信息, 测试误差将系统性偏小

-> 相当于"作弊"

数据集划分方法

1.留出法（Hold-out）

直接将数据集分成两部分：
- Train
- Test
分层抽样（stratified sampling）
- 各类别比例保持一致（防止类别不平衡）
常见比例：
- 2 / 3 ∼ 4 / 5 2/3 \sim 4/5 2/3∼4/5 作为训练集
- 剩余作为测试集

缺点: 对一次划分结果敏感, 方差较大

2.交叉验证（Cross Validation）

将数据集划分为 k k k 份
每次用 k − 1 k-1 k−1 份训练，1 份测试
重复 k k k 次，结果取平均
常用：
- k = 10 k=10 k=10
留一法（LOO, Leave-One-Out）
- k = m k=m k=m（样本总数）

缺点: 深度学习中较少使用交叉验证（计算成本太高）

优点: 用多次训练+测试来降低评估方差

3.自助法（Bootstrapping）

有放回抽样
从原始数据集 D D D 中：
- 每次随机抽取 1 个样本
- 重复 m m m 次
- 得到大小仍为 m m m 的新数据集 D ′ D' D′
性质：
- 原始数据集中约 36.8% 的样本不会出现在 D ′ D' D′ 中
- D ′ D' D′ → 训练集
- 未被抽到的 36.8 % 36.8\% 36.8% → 测试集

推导：

单次未被抽中的概率：
1 − 1 m 1 - \frac{1}{m} 1−m1

连续 m m m 次未被抽中：
( 1 − 1 m ) m \left(1 - \frac{1}{m}\right)^m (1−m1)m

极限：
lim ⁡ m → ∞ ( 1 − 1 m ) m = 1 e ≈ 0.368 \lim_{m\to\infty}\left(1-\frac{1}{m}\right)^m=\frac{1}{e}\approx0.368 m→∞lim(1−m1)m=e1≈0.368

参数调优（Parameter Tuning）

超参数 vs 参数

参数：模型学出来的（权重）

超参数：你事先设定的（学习率、正则化、网络深度等）

为什么需要验证集validation

train：拟合模型
validation：选模型 / 调参
test：一次性评估

理论上：

测试集test的标签我们不应该知道
只允许知道 train / validation 的标签

网格搜索

为每个超参数设置：

start
end
step

枚举所有组合，选验证集表现最优的

性能度量 Performance Measure

评估的相对性：

不同任务 → 不同指标
没有"万能指标"

1.混淆矩阵

	预测正例 (Pred=1)	预测负例 (Pred=0)
真实正例 (Actual=1)	TP（True Positive）	FN（False Negative）
真实负例 (Actual=0)	FP（False Positive）	TN（True Negative）

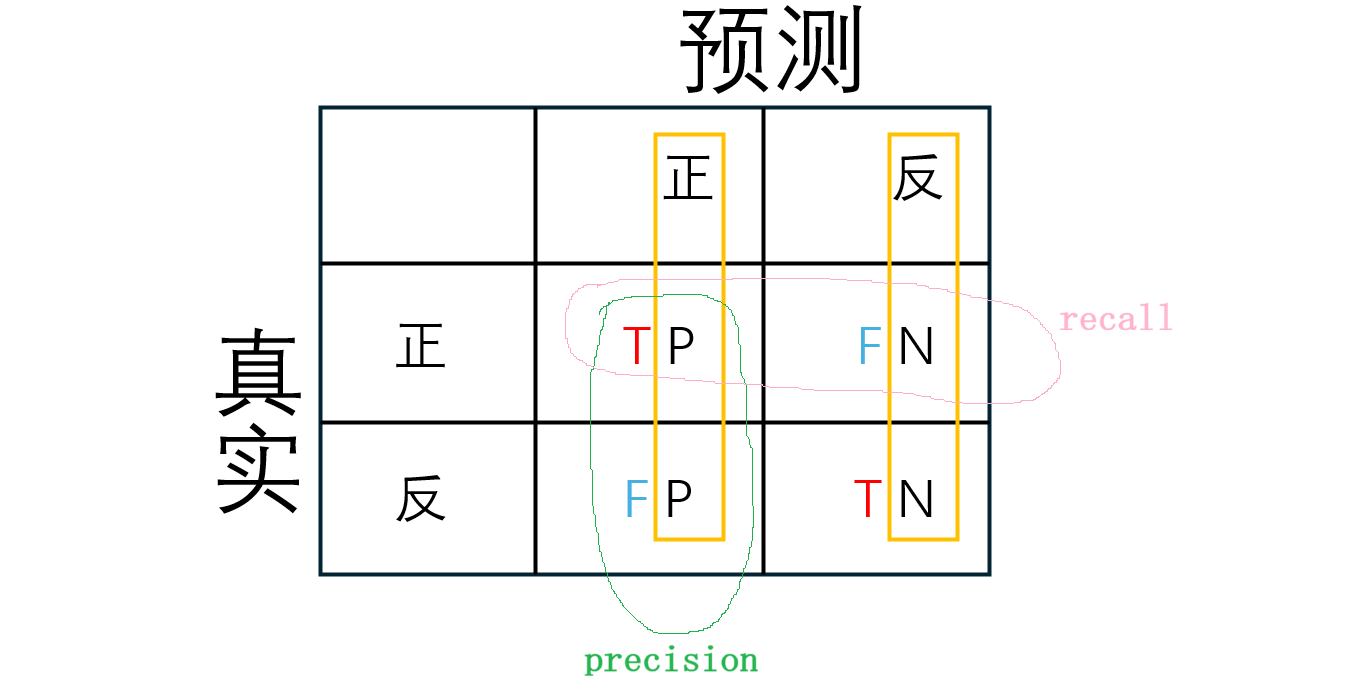
2.Precision（查准率）

"预测的可靠性":

从模型预测为正的样本 来看，有多少是真的
P = T P T P + F P P=\frac{TP}{TP+\mathbf{FP}} P=TP+FPTP
假阳性FP代价高时重视 Precision

例如：垃圾邮件识别，如果误杀正常邮件代价高
精度高意味着你发出的"正例"警告可信

3.Recall（召回率 / 查全率）

"检出率":

从实际正样本 来看，有多少被模型找出来
R = T P T P + F N R=\frac{TP}{TP+\mathbf{FN}} R=TP+FNTP
假阴性FN代价高时重视 Recall

医疗诊断：漏掉病人代价大
安全监控、杀毒软件：漏掉威胁代价大

4.权衡 Precision 与 Recall

分类器通常输出概率 p p p，并用阈值 t t t 决定正负：

p ≥ t p \ge t p≥t → 预测正
p < t p < t p<t → 预测负

规律：

阈值降低 → 更容易预测为正 → TP ↑, FP ↑
- Recall ↑ （更多正样本被找出来）
- Precision ↓ （假阳性增加）
阈值升高 → 更严格 → TP ↓, FP ↓
- Recall ↓
- Precision ↑

5. F1-score（综合指标）

综合考虑了 P P P和 R R R:

F1 是 调和平均 ，更偏向低的那个值
F 1 = 2 ∗ P ∗ R P + R = 2 ∗ T P m + T P − T N F1=\frac{2*P*R}{P+R}=\frac{2*TP}{m+TP-TN} F1=P+R2∗P∗R=m+TP−TN2∗TP
加权Fβ-score :
F β = ( 1 + β 2 ) P R β 2 P + R F_\beta=\frac{(1+\beta^2)PR}{\beta^2P+R} Fβ=β2P+R(1+β2)PR

β > 1 \beta > 1 β>1 → 更关注 Recall
β < 1 \beta < 1 β<1 → 更关注 Precision

宏平均 (Macro)

每个类别的指标先算平均
对类别不平衡敏感

m a c r o _ P = 1 n ∑ i = 1 n P i m a c r o _ R = 1 n ∑ i = 1 n R i m a c r o _ F 1 = 2 ∗ m a c r o _ P ∗ m a c r o _ R m a c r o _ P + m a c r o _ R macro\P = \frac{1}{n}\sum{i=1}^nP_i \\ macro\R = \frac{1}{n}\sum{i=1}^nR_i \\ macro\_F1 = \frac{2*macro\_P*macro\_R}{macro\_P+macro\_R} macro_P=n1i=1∑nPimacro_R=n1i=1∑nRimacro_F1=macro_P+macro_R2∗macro_P∗macro_R

微平均 (Micro)

将 TP、FP、FN 全部加起来再算 F1
对类别不平衡 不敏感

m i c r o _ P = T P ‾ T P ‾ + F P ‾ m i c r o _ R = T P ‾ T P ‾ + F N ‾ m i c r o _ F 1 = 2 ∗ m i c r o _ P ∗ m i c r o _ R m i c r o _ P + m i c r o _ R micro\_P=\frac{\overline{TP}}{\overline{TP}+\overline{FP}} \\ micro\_R=\frac{\overline{TP}}{\overline{TP}+\overline{FN}} \\ micro\_F1 = \frac{2*micro\_P*micro\_R}{micro\_P+micro\_R} micro_P=TP+FPTPmicro_R=TP+FNTPmicro_F1=micro_P+micro_R2∗micro_P∗micro_R

选择：

小类重要 → 宏平均
总体性能 → 微平均

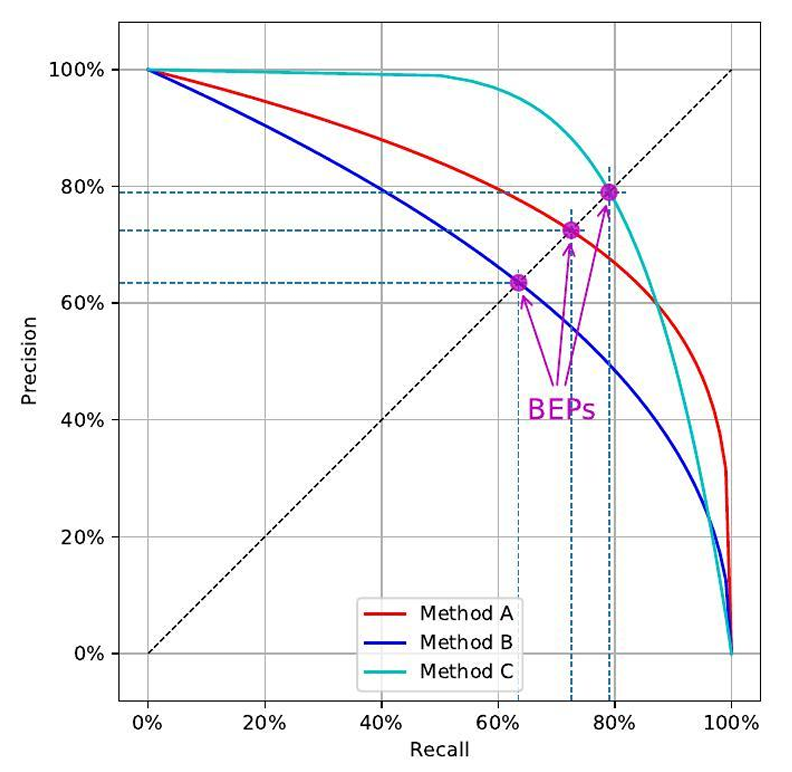
6. P-R 曲线 (Precision-Recall Curve)

横轴：Recall

纵轴：Precision

曲线越靠右上角 → 模型越好
如果一条曲线完全包住另一条 → 覆盖的模型在所有阈值下都更优
有时用 P=R 的点 作为折中指标

小样本或类别不平衡时比 ROC 更有价值

7. ROC 曲线 (Receiver Operating Characteristic)

横轴 FPR: false positive rate: 从实际负样本 来看，有多少被预测错了
F P R = F P T N + F P FPR=\frac{FP}{TN+FP} FPR=TN+FPFP

纵轴 TPR: true positive rate: 从实际正样本 来看，有多少被预测对了
T P R = T P T P + F N ( = R e c a l l ) TPR=\frac{TP}{TP+FN}(=Recall) TPR=TP+FNTP(=Recall)

阈值变化 → TPR, FPR 变化 → 绘制 ROC

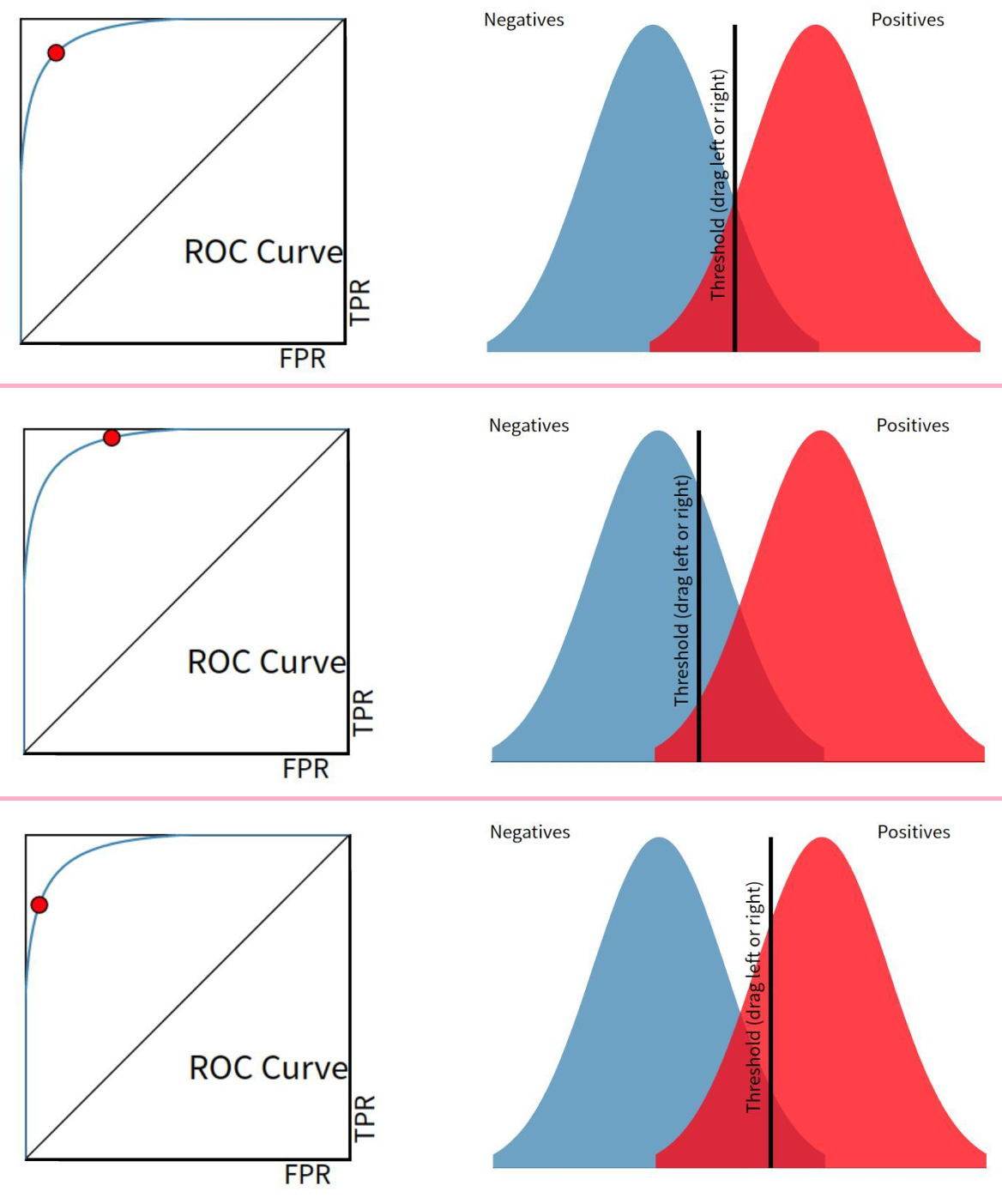
曲线越靠左上角 → 更优

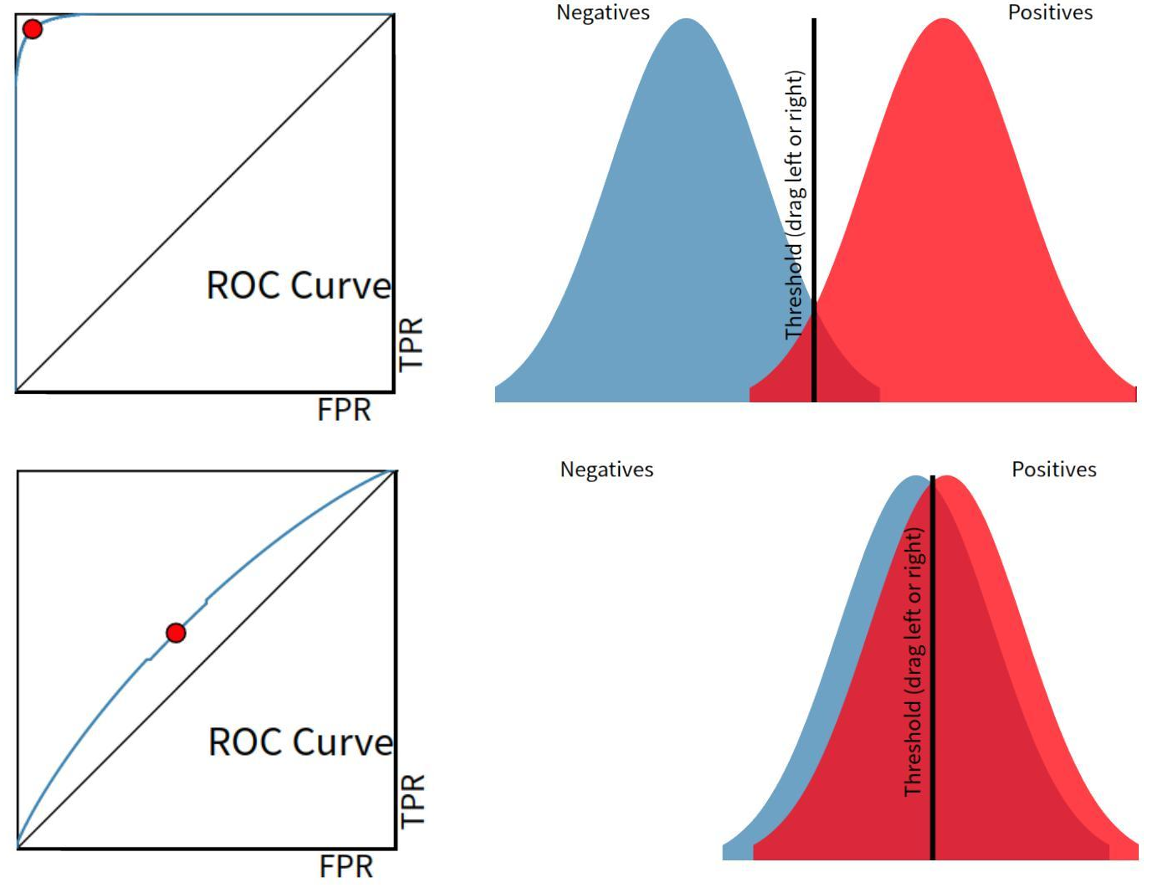
左上角：TPR 高，FPR 低 → "找到大部分正例，同时少误报负例"

对角线：随机猜测

总结比较

指标	关注	优势	劣势
Precision	预测正例可靠性	FP 代价大	对漏报不敏感
Recall	检出率	FN 代价大	FP 增加
F1-score	P/R 平衡	综合指标	无法体现不同业务权重
P-R 曲线	阈值敏感	小样本 & 不平衡	只反映正类性能
ROC 曲线	TPR/FPR 关系	类别不平衡鲁棒	对正类极小数据不敏感

[机器学习-从入门到入土] 模型评估与选择