本故事根据真实故事改编
故事开始
从前,在繁华的魔都上海,有一位姓姚的律师。在法庭上,他是法律的捍卫者,严谨、冷静,就像 Manacher 算法的第一步 "预处理字符串":他通过西装、法律证书和名校光环,在自己真实的人格缝隙中插入了无数个"#"字符。他在外界看来是绝对"对称"和"完美"的,没有人能看穿那层精心设计的虚假外壳。

每天,他都在维护一个巨大的 R R R(右边界) 。这个 R R R 是他的职业声望,也是他的保护伞。在 R R R 的内部,他利用 i _ m i r r o r i\_mirror i_mirror(对称点) 的原理,巧妙地复刻着社会精英的行为模板。他在 Telegram 的阴影里化名"猫中医",建立起一个名为"回文"的恐怖规则:他认为折磨弱小生命所带来的快感,必须像算法一样精准、对称且高效。他计算着每一只猫的痛苦指数,就像计算数组 P [ i ] P[i] P[i] 的半径,以此填充他内心深空的荒芜。

有一天,姚某不再满足于在已有的 R R R 范围内游走。他内心的恶意开始了 "中心扩展"(Center Expansion) 。他买下了第一台绞肉机,拿起了铁钎,欲望的半径 P [ i ] P[i] P[i] 开始疯狂向外探测。他不再满足于暗处的虐待,而是开始拍摄、上传、建立黑色产业链。他以为只要自己的 "律师身份" 这个 C C C(中心点) 足够稳固,他就可以无限扩张恶的边界,而不被外界察觉。

因为那样,他的行为触碰到了人类文明最底线的字符。当他在视频里将幼猫塞入绞肉机,当他疯狂地增加 P [ i ] P[i] P[i] 的数值时,他并没有意识到,算法中的 T [ i + 1 + P [ i ] ] T[i+1+P[i]] T[i+1+P[i]] 与 T [ i − 1 − P [ i ] ] T[i-1-P[i]] T[i−1−P[i]] 已经不再匹配。现实世界的良知与他的暴行产生了剧烈的冲突。那些被他诱捕的流浪猫、那些被他剖腹取胎的生命,成了无法被"对称"掉的血色证据。
因为那样,黑暗中的志愿者们化身为算法中的 检测机制 。他们不眠不休地追踪那些残忍的视频,比对每一处背景、每一个转账记录。姚某以为他能利用法律知识躲在 i < R i < R i<R 的安全区里,但他忘了,Manacher 算法的本质是为了暴露隐藏的模式。当成百上千份证据(网传 300 多部视频、4000 只猫的哀嚎)被汇聚成一个巨大的数组,他的伪装在逻辑面前轰然崩塌。

直到最后,舆论的巨浪冲破了他在法律界维持的 R R R(右边界) 。律所解聘、协会调查、社会性死亡------他的"中心点 C C C"被彻底移出。在这个瞬间,算法停止了。人们发现,这个所谓的"精英律师",其内心半径 P P P 里装载的不是正义,而是粘稠的鲜血和冰冷的铁屑。他的 MaxLen(最大回文长度) 记录的不是成就,而是他反人类罪行的深度。

从此以后,"猫中医"这个词成了一个带血的警示灯。它告诫世人:最完美的算法,也无法掩盖最扭曲的人性。 人们开始反思,如何在这个高度文明的社会中,及时识别那些利用 "预处理外壳" 伪装的恶魔。而那张 Manacher 流程图,也被贴在了道德的实验室里,提醒每一位执法者和观察者:当一个人的"扩张"开始践踏生命时,无论他的背景多么对称、逻辑多么严密,正义的算法终将计算出他罪恶的真值,并将其从人类文明的字符串中彻底剔除。

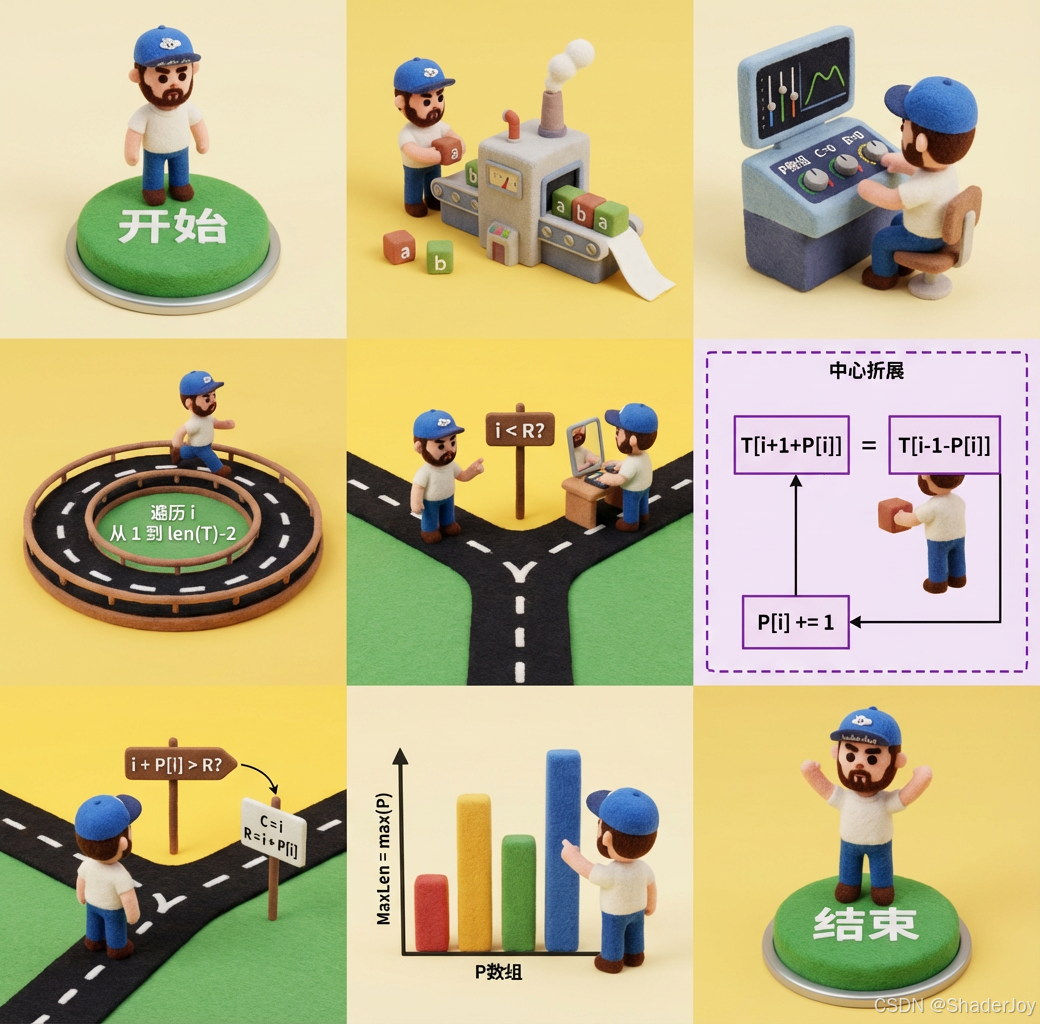
Manacher 算法流程图

Manacher 算法代码
python
def manacher(s):
# 步骤1:预处理------用#统一奇偶,^/$防越界
T = '^#' + '#'.join(s) + '#$'
n = len(T)
# 步骤2:初始化------P存半径,C/R为当前中心和右边界
P = [0] * n
C = R = 0
# 步骤3:遍历------逐个计算每个i的回文半径(跳过哨兵)
for i in range(1, n-2):
# 步骤4:对称复用------i在R内时,借i'的半径(i'=2C-i)
i_mirror = 2 * C - i # i的对称点
if i < R:
P[i] = min(R - i, P[i_mirror])
# 步骤5:扩展------尝试增大半径,直到字符不对称
while T[i + P[i] + 1] == T[i - P[i] - 1]:
P[i] += 1
# 步骤6:更新------若i的边界更大,更新C和R
if i + P[i] > R:
C, R = i, i + P[i]
# 步骤7:结果
# return max(P)
max_len, center = max((val, idx) for idx, val in enumerate(P))
start = (center - max_len) // 2
return s[start:start + max_len]算法速记小抄