Chapter 3: 大语言模型基础 Part 1：从 N-gram 到词嵌入

前两章分别介绍了智能体的定义和发展历史。本章将完全聚焦于大语言模型（LLM）本身，从最基础的原理出发，解答"现代智能体是如何思考的"这一关键问题。

3.1 语言模型与 Transformer 架构

3.1.1 从 N-gram 到 RNN

语言模型 (Language Model, LM) 是自然语言处理的核心，其根本任务是计算一个词序列（即一个句子）出现的概率。一个好的语言模型能够告诉我们什么样的句子是通顺的、自然的。在多智能体系统中，语言模型是智能体理解人类指令、生成回应的基础。

本节将回顾从经典的统计方法到现代深度学习模型的演进历程。

(1) 统计语言模型与 N-gram 的思想

在深度学习兴起之前，统计方法是语言模型的主流。其核心思想是，一个句子出现的概率，等于该句子中每个词出现的条件概率的连乘。

对于一个由词 w1,w2,...,wmw_{1},w_{2},...,w_{m}w1,w2,...,wm 构成的句子 SSS，其概率 P(S)P(S)P(S) 可以表示为概率的链式法则 ：
P(S)=P(w1,w2,...,wm)=P(w1)⋅P(w2∣w1)⋅P(w3∣w1,w2)⋅...⋅P(wm∣w1,...,wm−1)P(S)=P(w_{1},w_{2},...,w_{m})=P(w_{1})\cdot P(w_{2}|w_{1})\cdot P(w_{3}|w_{1},w_{2})\cdot...\cdot P(w_{m}|w_{1},...,w_{m-1})P(S)=P(w1,w2,...,wm)=P(w1)⋅P(w2∣w1)⋅P(w3∣w1,w2)⋅...⋅P(wm∣w1,...,wm−1)

💡 注解：

这个公式在理论上是完美的，但在工程上直接计算几乎是不可能的。因为随着句子变长，像 P(wm∣w1,...,wm−1)P(w_{m}|w_{1},...,w_{m-1})P(wm∣w1,...,wm−1) 这样的条件概率参数空间会呈指数级爆炸，且很多长序列 w1,...,wm−1w_{1},...,w_{m-1}w1,...,wm−1 可能从未在训练数据中出现过，导致概率为 0（数据稀疏问题）。

马尔可夫假设 (Markov Assumption)

为了解决上述计算难题，研究者引入了马尔可夫假设。其核心思想是：我们不必回溯一个词的全部历史，可以近似地认为，一个词的出现概率只与它前面有限的 n−1n-1n−1 个词有关 。基于这个假设建立的语言模型，称为 N-gram 模型 。这里的 "NNN" 代表我们考虑的上下文窗口大小。

• Bigram (当 N=2 时) ：这是最简单的情况，假设一个词的出现只与它前面的一个词有关。链式法则近似为：

P(wi∣w1,...,wi−1)≈P(wi∣wi−1)P(w_{i}|w_{1},...,w_{i-1})\approx P(w_{i}|w_{i-1})P(wi∣w1,...,wi−1)≈P(wi∣wi−1)

• Trigram (当 N=3 时) ：假设一个词的出现只与它前面的两个词有关：

P(wi∣w1,...,wi−1)≈P(wi∣wi−2,wi−1)P(w_{i}|w_{1},...,w_{i-1})\approx P(w_{i}|w_{i-2},w_{i-1})P(wi∣w1,...,wi−1)≈P(wi∣wi−2,wi−1)

最大似然估计 (Maximum Likelihood Estimation, MLE)

这些概率可以通过在大型语料库中进行最大似然估计来计算。思想非常直观：最可能出现的，就是我们在数据中看到次数最多的。

以 Bigram 模型为例，计算在词 wi−1w_{i-1}wi−1 出现后，下一个词是 wiw_{i}wi 的概率 P(wi∣wi−1)P(w_{i}|w_{i-1})P(wi∣wi−1)：

P(wi∣wi−1)=Count(wi−1,wi)Count(wi−1)P(w_{i}|w_{i-1})=\frac{Count(w_{i-1},w_{i})}{Count(w_{i-1})}P(wi∣wi−1)=Count(wi−1)Count(wi−1,wi)

其中：

• Count(wi−1,wi)Count(w_{i-1},w_{i})Count(wi−1,wi)：表示词对 (wi−1,wi)(w_{i-1},w_{i})(wi−1,wi) 在语料库中连续出现的总次数。
• Count(wi−1)Count(w_{i-1})Count(wi−1)：表示单个词 wi−1w_{i-1}wi−1 在语料库中出现的总次数。1

---

手动计算演练

为了让这个过程更具体，我们来手动进行一次计算。
假设语料库（仅包含两句话）：

1. datawhale agent learns
2. datawhale agent works

目标 ：使用 Bigram (N=2N=2N=2) 模型，估算句子 datawhale agent learns 出现的概率。

Step 1: 计算第一个词的概率 P(datawhale)P(datawhale)P(datawhale)

datawhale 出现了 2 次，总词数是 6。

P(datawhale)=26≈0.333P(datawhale) = \frac{2}{6} \approx 0.333P(datawhale)=62≈0.333

Step 2: 计算条件概率 P(agent∣datawhale)P(agent|datawhale)P(agent∣datawhale)

词对 datawhale agent 出现了 2 次，前缀词 datawhale 出现了 2 次。

P(agent∣datawhale)=Count(datawhale agent)Count(datawhale)=22=1P(agent|datawhale)=\frac{Count(datawhale~agent)}{Count(datawhale)}=\frac{2}{2}=1P(agent∣datawhale)=Count(datawhale)Count(datawhale agent)=22=1

Step 3: 计算条件概率 P(learns∣agent)P(learns|agent)P(learns∣agent)

词对 agent learns 出现了 1 次，前缀词 agent 出现了 2 次（分别在 learns 和 works 之前）。

P(learns∣agent)=Count(agent learns)Count(agent)=12=0.5P(learns|agent)=\frac{Count(agent~learns)}{Count(agent)}=\frac{1}{2}=0.5P(learns∣agent)=Count(agent)Count(agent learns)=21=0.5

Step 4: 概率连乘

P(datawhale agent learns)≈0.333⋅1⋅0.5≈0.167P(datawhale~agent~learns)\approx 0.333 \cdot 1 \cdot 0.5 \approx 0.167P(datawhale agent learns)≈0.333⋅1⋅0.5≈0.167

---

代码实现 (Python)

以下代码完全复现了上述计算过程，清晰展示了统计语言模型的内部逻辑 2：

import collections

# 示例语料库，与上方案例讲解中的语料库保持一致
corpus = "datawhale agent learns datawhale agent works"
tokens = corpus.split()
total_tokens = len(tokens)

# 第一步: 计算 P(datawhale)
count_datawhale = tokens.count('datawhale')
p_datawhale = count_datawhale / total_tokens
print(f"第一步: P(datawhale) = {count_datawhale}/{total_tokens} = {p_datawhale:.3f}")

# 第二步: 计算 P(agent|datawhale)
# 先计算 bigrams 用于后续步骤
bigrams = zip(tokens, tokens[1:])
bigram_counts = collections.Counter(bigrams)

count_datawhale_agent = bigram_counts[('datawhale', 'agent')]
# count_datawhale 已在第一步计算
p_agent_given_datawhale = count_datawhale_agent / count_datawhale
print(f"第二步: P(agent|datawhale) = {count_datawhale_agent}/{count_datawhale} = {p_agent_given_datawhale:.3f}")

# 第三步: 计算 P(learns|agent)
count_agent_learns = bigram_counts[('agent', 'learns')]
count_agent = tokens.count('agent')
p_learns_given_agent = count_agent_learns / count_agent
print(f"第三步: P(learns|agent) = {count_agent_learns}/{count_agent} = {p_learns_given_agent:.3f}")

# 最后: 将概率连乘
p_sentence = p_datawhale * p_agent_given_datawhale * p_learns_given_agent
print(f"最后: P('datawhale agent learns') = {p_datawhale:.3f} * {p_agent_given_datawhale:.3f} * {p_learns_given_agent:.3f} = {p_sentence:.3f}")

运行结果：

第一步: P(datawhale) = 2/6 = 0.333
第二步: P(agent|datawhale) = 2/2 = 1.000
第三步: P(learns|agent) = 1/2 = 0.500
最后: P('datawhale agent learns') = 0.333 * 1.000 * 0.500 = 0.167

N-gram 模型的致命缺陷

1. 数据稀疏性 (Sparsity)：如果一个词序列从未在语料库中出现，其概率估计就为 0。
2. 泛化能力差 ：模型无法理解词与词之间的语义相似性。例如，即使模型见过 agent learns，当遇到 robot learns 时，如果 robot 未出现过，模型无法利用 agent 和 robot 的相似性进行推断。

💡 深度解析 ：N-gram 的根本缺陷在于它将词视为孤立、离散的符号 （One-hot 编码思维）。为了克服这个问题，研究者转向了神经网络，提出用连续的向量来表示词。

---

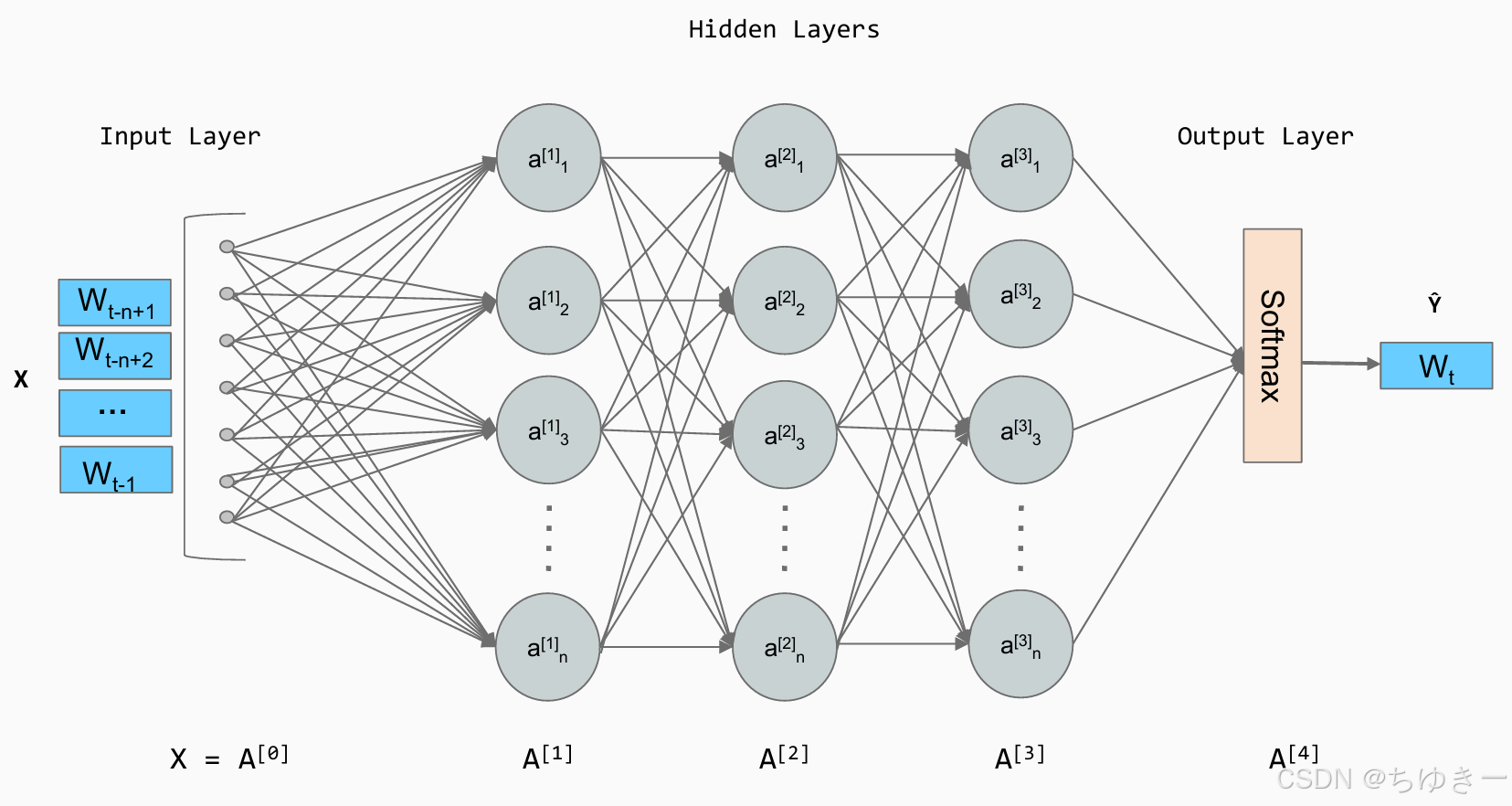
(2) 神经网络语言模型与词嵌入

2003年，Bengio 等人提出的前馈神经网络语言模型 (Feedforward Neural Network Language Model) 是这一领域的里程碑。
核心思想：

1. 构建一个语义空间 ：创建一个高维的连续向量空间，将每个词映射为一个点（向量），称为词嵌入 (Word Embedding) 。在这个空间里，语义相近的词（如 agent 和 robot）距离更近。
2. 学习映射函数 ：利用神经网络拟合一个函数，输入前 n−1n-1n−1 个词的向量，输出下一个词的概率分布。
   
   词向量的数学度量：余弦相似度
   一旦将词转换为向量，就可以使用余弦相似度 (Cosine Similarity) 来度量它们的关系：
   similarity(a⃗,b⃗)=cos(θ)=a⃗⋅b⃗∣a⃗∣∣b⃗∣similarity(\vec{a},\vec{b})=cos(\theta)=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}similarity(a ,b )=cos(θ)=∣a ∣∣b ∣a ⋅b

• 1 (0°)：完全相关。

• 0 (90°)：毫无关系（正交）。

• -1 (180°)：完全负相关。

经典案例：词向量的代数运算

一个著名的例子展示了词向量捕捉到的语义关系：

vector(′King′)−vector(′Man′)+vector(′Woman′)≈vector(′Queen′)vector('King') - vector('Man') + vector('Woman') \approx vector('Queen')vector(′King′)−vector(′Man′)+vector(′Woman′)≈vector(′Queen′)

这好比在语义空间进行平移，证明了词嵌入能够学习到"性别"、"皇室"等抽象概念。

代码实现：词向量运算

以下代码模拟了如何在向量空间中进行语义运算 ：

import numpy as np

# 假设我们已经学习到了简化的二维词向量
embeddings = {
    "king": np.array([0.9, 0.8]),
    "queen": np.array([0.9, 0.2]),
    "man": np.array([0.7, 0.9]),
    "woman": np.array([0.7, 0.3])
}

def cosine_similarity(vec1, vec2):
    dot_product = np.dot(vec1, vec2)
    norm_product = np.linalg.norm(vec1) * np.linalg.norm(vec2)
    return dot_product / norm_product

# king - man + woman
result_vec = embeddings["king"] - embeddings["man"] + embeddings["woman"]

# 计算结果向量与 "queen" 的相似度
sim = cosine_similarity(result_vec, embeddings["queen"])

print(f"king - man + woman 的结果向量: {result_vec}")
print(f"该结果与 'queen' 的相似度: {sim:.4f}")

运行结果：

king - man + woman 的结果向量: [0.9 0.2]
该结果与 'queen' 的相似度: 1.0000

---