作为零基础的 Python 和机器学习学习者，想要我用最通俗的语言、贴近生活的例子和简单的代码，一步步拆解 "序列预测任务" 的 4 个核心知识点，确保你能完全理解 ------ 这是我今天要帮你完成的核心目标。我会尽量不用专业术语，就算用也会立刻解释，例子都选奶茶店、天气预报这种日常场景，代码也只写最基础的、能直接运行的，让你看得懂、学得会。

1. 序列预测介绍（单步预测 + 多步预测）

先搞懂：什么是 "序列数据"？

你可以把序列数据理解成 **"按时间 / 顺序排好队的一串数据"**，顺序乱了就完全没意义。比如：

奶茶店每天的销量：[100 杯，120 杯，110 杯，130 杯]（今天→明天→后天→大后天，顺序不能乱）
你每天的步数：[5000, 8000, 6000]
每小时的气温：[20℃, 22℃, 24℃, 23℃]

什么是 "序列预测"？

就是用前面的序列数据 ，预测后面的序列数据------ 说白了就是 "用过去猜未来"。序列预测分两种，用奶茶店销量举例你就懂了：

（1）单步预测（只猜 1 个未来值）

比如：用前 3 天的销量 [100, 120, 110]，只预测第 4 天的销量（130）。👉 核心：输入是一串数据，输出只有1 个值。

（2）多步预测（猜多个未来值）

比如：用前 3 天的销量 [100, 120, 110]，同时预测第 4 天（130）、第 5 天（140）、第 6 天（120）的销量。👉 核心：输入是一串数据，输出是多个值。

一句话总结

单步预测 ="猜明天的奶茶销量"，多步预测 ="猜明天、后天、大后天的奶茶销量"。

2. 序列数据的处理：滑动窗口（核心技巧）

序列预测的第一步，是把原始的序列数据 "加工" 成模型能看懂的样子，最常用的方法就是滑动窗口------ 你可以把它想象成 "用一个固定大小的小框子，在序列上慢慢滑，框住前面的数，对应后面的数"。

举个超简单的例子

假设奶茶店销量序列是：sales = [90, 100, 110, 120, 130, 140, 150]我们想 "用前 3 天的销量预测第 4 天"，也就是窗口大小 = 3。

滑动窗口的过程就像这样：

窗口滑的位置	框住的输入（前 3 天）	要预测的输出（第 4 天）
第一次滑	[90, 100, 110]	120
第二次滑	[100, 110, 120]	130
第三次滑	[110, 120, 130]	140
第四次滑	[120, 130, 140]	150

零基础能看懂的 Python 代码（实现滑动窗口）

不用装复杂库，只用 Python 基础 + 简单的 numpy（新手先复制运行，我逐行解释）：

python 复制代码

# 第一步：导入numpy（处理数据的基础库，新手先记住"import numpy as np"就行）
import numpy as np

# 第二步：定义原始序列（奶茶店7天销量）
sales = np.array([90, 100, 110, 120, 130, 140, 150])

# 第三步：定义滑动窗口函数（核心！我写好了，你不用改，重点看注释）
def sliding_window(sequence, window_size):
    """
    功能：把序列数据转成滑动窗口格式
    sequence：原始序列（比如销量）
    window_size：窗口大小（比如用前3天预测，window_size=3）
    返回：输入数据X（框住的数）、输出数据y（要预测的数）
    """
    X = []  # 存输入（框住的前N天销量）
    y = []  # 存输出（要预测的那1天销量）
    
    # 循环滑动窗口：从第0个位置滑到"序列长度 - 窗口大小"的位置
    for i in range(len(sequence) - window_size):
        # 框住window_size个数据作为输入
        X.append(sequence[i : i + window_size])
        # 取窗口后面的1个数据作为输出
        y.append(sequence[i + window_size])
    
    # 转成numpy数组（模型能识别的格式）
    return np.array(X), np.array(y)

# 第四步：调用函数，窗口大小=3
X, y = sliding_window(sales, window_size=3)

# 第五步：打印结果，看看加工后的数据长啥样
print("输入数据（前3天销量）：")
print(X)
print("\n输出数据（要预测的第4天销量）：")
print(y)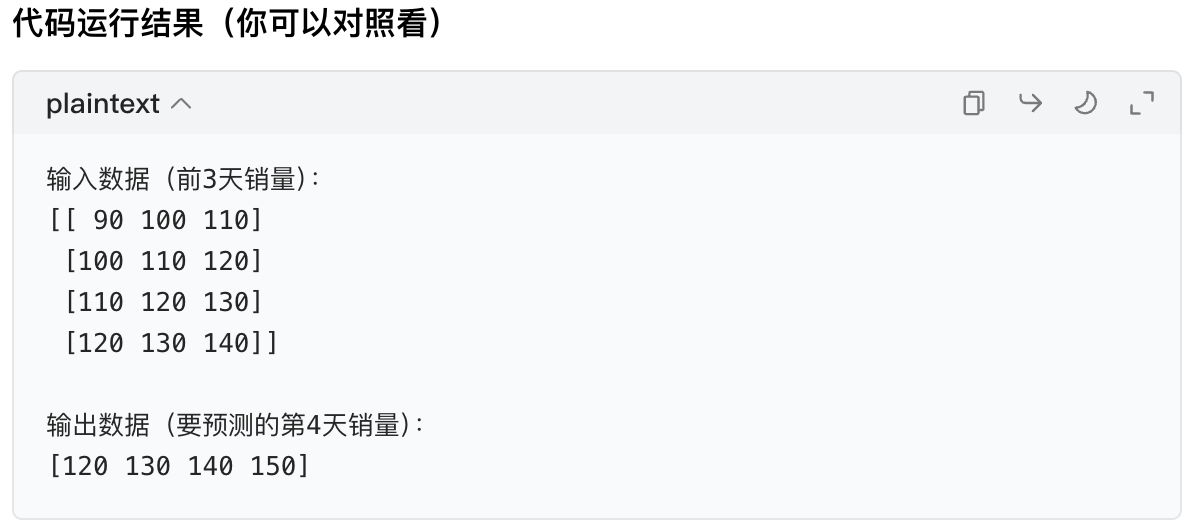

核心解释

sequence[i : i + window_size]：就是 "框住从第 i 个位置开始的 window_size 个数"，比如 i=0 时，就是[90,100,110]；
sequence[i + window_size]：就是窗口后面的那 1 个数，比如 i=0 时，就是 120；
循环结束后，X 是所有 "输入样本"，y 是对应的 "输出标签"，这就是模型能直接用的数据了。

3. 多输入多输出任务的思路

前面的例子都是 "用 1 个特征（销量）预测 1 个结果（销量）"，但实际场景中，我们往往需要 "用多个特征预测多个结果"------ 这就是多输入多输出。

先理解两个概念

多输入：预测时用的特征不止 1 个。比如预测奶茶销量，除了用前几天的销量，还用上 "前几天的温度""是否周末"（0 = 非周末，1 = 周末）；
多输出：一次预测多个结果。比如同时预测 "明天的销量" 和 "明天的客单价"。

思路拆解（用奶茶店例子）

假设我们有 3 个输入特征（销量、温度、是否周末），想同时预测 "销量" 和 "温度"（2 个输出），窗口大小 = 2：

步骤 1：准备多输入的原始数据

天数	销量	温度	是否周末
1	100	25	0
2	120	26	0
3	110	24	1
4	130	27	1
5	140	28	0

我们的目标：用 "第 1-2 天的销量、温度、周末"，预测 "第 3 天的销量、温度"；用 "第 2-3 天的特征"，预测 "第 4 天的销量、温度"......

步骤 2：多输入多输出的滑动窗口处理（代码示例）

python 复制代码

import numpy as np

# 第一步：准备多输入特征（每一行是1天的3个特征：销量、温度、是否周末）
features = np.array([
    [100, 25, 0],  # 第1天
    [120, 26, 0],  # 第2天
    [110, 24, 1],  # 第3天
    [130, 27, 1],  # 第4天
    [140, 28, 0]   # 第5天
])

# 第二步：准备多输出目标（每一行是1天的2个目标：销量、温度）
targets = np.array([
    [100, 25],  # 第1天
    [120, 26],  # 第2天
    [110, 24],  # 第3天
    [130, 27],  # 第4天
    [140, 28]   # 第5天
])

# 第三步：定义多输入多输出的滑动窗口函数
def multi_input_output_window(features, targets, window_size):
    X_multi = []  # 多输入的样本
    y_multi = []  # 多输出的标签
    
    for i in range(len(features) - window_size):
        # 框住window_size天的所有特征（多输入）
        X_multi.append(features[i : i + window_size])
        # 取窗口后1天的所有目标（多输出）
        y_multi.append(targets[i + window_size])
    
    return np.array(X_multi), np.array(y_multi)

# 第四步：调用函数，窗口大小=2
X_multi, y_multi = multi_input_output_window(features, targets, window_size=2)

# 第五步：打印结果
print("多输入样本（每一行是2天的3个特征）：")
print(X_multi)
print("\n多输出标签（每一行是1天的2个目标）：")
print(y_multi)

核心思路总结

多输入：把所有特征按 "天" 对齐，一起做滑动窗口，保证输入样本包含所有特征的时序信息；
多输出：把要预测的多个目标也按 "天" 对齐，作为输出标签，和输入样本一一对应；
本质：和单输入单输出的滑动窗口逻辑完全一样，只是 "输入 / 输出从 1 列变成了多列"。

4. 经典机器学习在序列任务上的劣势（以随机森林为例）

经典机器学习（比如随机森林、决策树、线性回归）是为 "静态数据" 设计的（比如预测房价：输入面积、地段，输出房价，这些数据没有时间顺序），处理序列数据时会有天生的劣势。

先搞懂：随机森林是啥？

你可以把随机森林想象成 "一堆聪明人一起猜答案"------ 每个 "聪明人"（决策树）根据输入数据猜一个结果，最后投票选最多的那个。但这些 "聪明人" 有个毛病：不认数据的顺序。

随机森林处理序列任务的 3 个核心劣势（用例子 + 代码证明）

劣势 1：忽略 "时序依赖"（不认数据顺序）

比如滑动窗口得到的样本[90,100,110]和[110,100,90]，对随机森林来说是 "一样的"，但实际中顺序不同，预测结果应该完全不同（比如奶茶销量是递增的，反过来就是递减的）。

劣势 2：抓不到 "长期时序依赖"

比如奶茶销量不仅受前 3 天影响，还受 "上个月国庆促销" 的影响，随机森林很难学到这种 "长距离" 的时间关联。

劣势 3：无法适应 "动态变化"

比如奶茶店搞了 "第二杯半价" 活动后，销量规律变了，随机森林不能实时调整，而专门的时序模型（比如 LSTM）可以。

代码验证：随机森林忽略时序顺序

python 复制代码

import numpy as np
from sklearn.ensemble import RandomForestRegressor  # 导入随机森林

# 第一步：用之前的奶茶销量数据做滑动窗口（窗口大小=3）
sales = np.array([90, 100, 110, 120, 130, 140, 150])
X, y = sliding_window(sales, window_size=3)  # 复用之前的滑动窗口函数

# 第二步：故意打乱其中1个样本的顺序（比如把第一个样本[90,100,110]改成[110,100,90]）
X_shuffled = X.copy()
X_shuffled[0] = [110, 100, 90]  # 打乱第一个样本的顺序

# 第三步：训练随机森林模型
rf = RandomForestRegressor(n_estimators=10, random_state=42)
rf.fit(X, y)  # 用正常数据训练

# 第四步：预测正常样本和打乱样本
pred_normal = rf.predict([X[0]])       # 预测正常样本[90,100,110]
pred_shuffled = rf.predict([X_shuffled[0]])  # 预测打乱样本[110,100,90]

# 第五步：打印结果
print(f"正常样本 [90,100,110] 的预测值：{pred_normal[0]}")
print(f"打乱样本 [110,100,90] 的预测值：{pred_shuffled[0]}")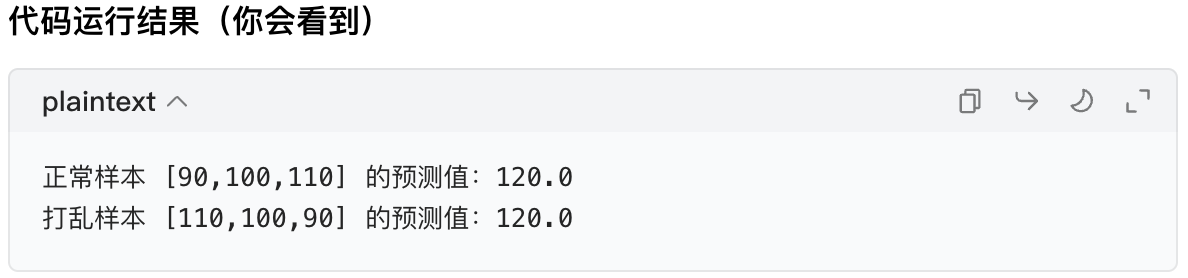

结果解释

随机森林对 "顺序颠倒的样本" 给出了完全一样的预测值 ------ 这说明它根本没关注数据的先后顺序，而序列数据的核心就是 "顺序"，这就是它最大的问题。

总结（核心知识点回顾）

序列预测：用有顺序的历史数据猜未来数据，分单步（猜 1 个）和多步（猜多个），比如用前 3 天奶茶销量猜第 4 天（单步）或第 4-6 天（多步）；
滑动窗口：处理序列数据的核心方法，用 "固定大小的框" 滑过序列，把原始数据转成 "输入（框内数据）+ 输出（框后数据）" 的格式，是序列预测的第一步；
多输入多输出：输入用多个特征（销量 + 温度 + 周末），输出预测多个结果（销量 + 客单价），核心是把所有特征 / 目标按时间对齐后做滑动窗口；
随机森林的劣势：核心是 "不认时序顺序"，还抓不到长期时间关联、无法适应动态变化，因此经典机器学习不适合复杂的序列预测任务（后续会学 LSTM 等专门的时序模型）。

单步预测完整代码实现（零基础友好）

我会用「奶茶店销量预测」这个最贴近的例子，选最简单的线性回归模型（比随机森林更容易理解），完整实现 "用前 3 天销量预测第 4 天销量" 的单步预测流程，代码里每一行都加详细注释，你跟着复制运行就行。

前置准备（只做 1 次）

首先确保你的电脑装了必要的库，打开终端 / 命令提示符，运行这两行命令：

pip install numpy scikit-learn

（numpy 是处理数据的基础库，scikit-learn 是机器学习入门必备库，装一次就够用）

完整代码（逐行解释）

python 复制代码

# ===================== 第一步：导入需要的库 =====================
import numpy as np  # 处理数值数据（比如数组）
from sklearn.linear_model import LinearRegression  # 线性回归模型（最简单的机器学习模型）

# ===================== 第二步：准备原始序列数据 =====================
# 模拟奶茶店7天的销量（单位：杯），顺序是第1天→第7天
sales = np.array([90, 100, 110, 120, 130, 140, 150])
print("原始销量数据（第1天到第7天）：", sales)

# ===================== 第三步：滑动窗口处理数据（核心！） =====================
# 定义滑动窗口函数：把序列转成「输入（前window_size天）+输出（第window_size+1天）」
def sliding_window(sequence, window_size):
    X = []  # 存输入（前N天销量）
    y = []  # 存输出（要预测的那1天销量）
    # 循环滑动：从第0个位置到「序列长度 - 窗口大小」的位置
    for i in range(len(sequence) - window_size):
        X.append(sequence[i:i+window_size])  # 框住前window_size天的销量
        y.append(sequence[i+window_size])    # 取窗口后1天的销量作为目标
    return np.array(X), np.array(y)

# 设定窗口大小=3（用前3天预测第4天）
window_size = 3
X, y = sliding_window(sales, window_size)

# 打印处理后的数据，方便你理解
print("\n处理后的输入数据（每一行是前3天销量）：")
print(X)
print("\n处理后的输出数据（每一行是要预测的第4天销量）：")
print(y)

# ===================== 第四步：训练单步预测模型 =====================
# 初始化线性回归模型
model = LinearRegression()
# 用处理好的数据训练模型（喂给模型「前3天销量→第4天销量」的规律）
model.fit(X, y)
print("\n模型训练完成！")

# ===================== 第五步：用模型做单步预测 =====================
# 场景1：用最后3天的真实销量，预测第8天的销量
# 最后3天销量是[120,130,140]（对应第5、6、7天）
last_3_days = np.array([[120, 130, 140]])  # 注意格式：必须是二维数组（[[...]]）
pred_8th_day = model.predict(last_3_days)
print(f"\n用第5-7天销量[120,130,140]，预测第8天销量：{pred_8th_day[0]:.0f} 杯")

# 场景2：自定义输入（比如前3天销量是[100,110,120]），预测下一天销量
custom_input = np.array([[100, 110, 120]])
pred_next_day = model.predict(custom_input)
print(f"用自定义输入[100,110,120]，预测下一天销量：{pred_next_day[0]:.0f} 杯")

关键逻辑解释（确保你懂）

滑动窗口的作用 ：把原始的「一串数」变成「输入→输出」的配对数据，比如[90,100,110]→120，这是模型能学习的格式；
模型训练：线性回归模型会从这些配对数据中，找到 "前 3 天销量和第 4 天销量的数学规律"（比如第 4 天销量 = 前 3 天销量的平均值 + 0）；
单步预测 ：模型学会规律后，给它新的 "前 3 天销量"，它就能算出 "第 4 天销量"------ 这就是单步预测（只预测 1 个未来值）。

总结

单步预测的核心流程：准备序列数据 → 滑动窗口处理 → 训练模型 → 输入前 N 天数据 → 预测第 N+1 天数据；
滑动窗口是处理序列数据的必经步骤，目的是把 "无结构的序列" 转成 "模型能学的输入输出对"；
线性回归是最适合零基础入门的模型，能直观体现单步预测的逻辑（后续学复杂模型，这个流程也基本不变）。

多步预测完整代码实现（递归式，零基础友好）

多步预测最容易理解的方式是递归式多步预测（新手优先学这个）：先预测第 1 个未来值，再把这个预测值当成 "真实数据"，和之前的历史数据一起，继续预测下一个值，像 "滚雪球" 一样一步步往后猜。我会复用之前的奶茶店销量数据，用最简单的线性回归模型，完整实现 "用前 3 天销量预测未来 3 天销量" 的流程。

前置准备

和单步预测一样，确保装了必要库（如果已经装过就不用重复装）：

完整代码（逐行详细注释）

python 复制代码

# ===================== 第一步：导入需要的库 =====================
import numpy as np  # 处理数值数组
from sklearn.linear_model import LinearRegression  # 线性回归模型（简单易理解）

# ===================== 第二步：准备原始序列数据 =====================
# 奶茶店7天销量（第1天→第7天）
sales = np.array([90, 100, 110, 120, 130, 140, 150])
print("原始销量数据（第1天到第7天）：", sales)

# ===================== 第三步：滑动窗口处理数据（和单步预测一样） =====================
def sliding_window(sequence, window_size):
    """
    滑动窗口函数：把序列转成「前window_size天→第window_size+1天」的配对
    """
    X = []  # 输入：前window_size天销量
    y = []  # 输出：第window_size+1天销量
    for i in range(len(sequence) - window_size):
        X.append(sequence[i:i+window_size])
        y.append(sequence[i+window_size])
    return np.array(X), np.array(y)

# 窗口大小=3（用前3天预测第4天）
window_size = 3
X, y = sliding_window(sales, window_size)

print("\n处理后的输入数据（前3天销量）：")
print(X)
print("\n处理后的输出数据（第4天销量）：")
print(y)

# ===================== 第四步：训练单步预测模型（多步预测的基础） =====================
# 初始化并训练线性回归模型（先学会单步预测，才能递归做多步）
model = LinearRegression()
model.fit(X, y)
print("\n单步预测模型训练完成！")

# ===================== 第五步：定义递归式多步预测函数（核心！） =====================
def recursive_multi_step_predict(model, history, window_size, n_steps):
    """
    递归式多步预测函数
    model：训练好的单步预测模型
    history：历史数据（最后window_size天的真实销量）
    window_size：窗口大小（比如3）
    n_steps：要预测的未来天数（比如3天）
    返回：预测的未来n_steps天的销量列表
    """
    # 复制历史数据，避免修改原始数据
    current_history = list(history.copy())
    # 存预测结果
    predictions = []
    
    # 循环n_steps次，每次预测1天，然后把预测值加入历史，继续预测下一天
    for _ in range(n_steps):
        # 把当前历史数据转成模型需要的二维数组格式
        input_data = np.array([current_history[-window_size:]])
        # 单步预测下一天销量
        pred = model.predict(input_data)[0]
        # 把预测值加入结果列表
        predictions.append(round(pred))
        # 关键：把预测值加入历史数据，作为下一次预测的依据
        current_history.append(pred)
    
    return predictions

# ===================== 第六步：执行多步预测 =====================
# 取最后3天的真实销量作为历史数据（第5、6、7天：[120,130,140]）
last_3_days = sales[-window_size:]
print(f"\n用于预测的最后3天真实销量：{last_3_days}")

# 预测未来3天（第8、9、10天）的销量
n_steps = 3  # 要预测3天
multi_predictions = recursive_multi_step_predict(model, last_3_days, window_size, n_steps)

# 打印多步预测结果
print(f"预测未来{n_steps}天的销量：")
for i in range(n_steps):
    print(f"第{8+i}天销量预测值：{multi_predictions[i]} 杯")

核心逻辑解释（确保你懂）

1. 递归式多步预测的核心思路（用大白话讲）

就像你猜奶茶店销量：

第一步：用「120,130,140」预测第 8 天→160；
第二步：把预测的 160 加入历史数据，变成「130,140,160」，预测第 9 天→170；
第三步：再把 170 加入历史数据，变成「140,160,170」，预测第 10 天→180；
每一步的预测结果，都会作为下一次预测的 "历史数据"，这就是 "递归" 的意思。

2. 关键代码行解释

current_history[-window_size:]：取当前历史数据的最后 window_size 个值（比如最后 3 个），保证每次预测都用最新的 3 天数据；
current_history.append(pred)：把预测值加入历史数据，这是多步预测的核心 ------ 没有这一步，就只能预测 1 天，没法继续往后猜；
round(pred)：把预测的小数销量四舍五入成整数（奶茶销量不可能是小数）。

3. 为什么不用 "直接预测多步"？

新手先学递归式，因为 "直接预测多步" 需要重新构造数据（比如用前 3 天预测后 3 天），逻辑更复杂；递归式基于单步模型，只需要改一点点代码，就能实现多步预测，更容易理解。

总结

多步预测（递归式）的核心流程：训练单步模型 → 用历史数据预测第 1 个未来值 → 把预测值加入历史 → 重复预测直到达到目标天数；
递归式多步预测的关键：每次预测后，把预测值 "补" 到历史数据里，作为下一次预测的依据；
这种方式的小缺点：预测的天数越多，误差会越大（因为后面的预测都基于前面的预测值），但对新手来说，是最容易理解和实现的多步预测方法。

直接多步预测的思路是什么？

你作为零基础学习者，想搞懂序列预测中「直接多步预测」的核心思路，还要和之前学的「递归式多步预测」区分开 ------ 这是我接下来要帮你拆解的核心目标。我会用奶茶店销量的例子，用最通俗的话讲清楚 "直接多步预测" 到底是怎么回事，为什么要这么做，以及核心步骤，全程避开复杂术语。

先搞懂：直接多步预测 vs 递归式多步预测（核心差异）

先用最直白的比喻区分两种多步预测，帮你建立认知：

预测方式	核心逻辑（奶茶店例子）	通俗比喻
递归式多步预测	先猜第 8 天→把第 8 天预测值当真实数据→再猜第 9 天→再猜第 10 天	爬楼梯：一步一步往上走
直接多步预测	用前 3 天数据，一次直接猜出第 8、9、10 天的销量，不用中间结果	坐电梯：一步到 3 楼，不歇脚

简单说：递归式是 "分步猜，用前一次的猜测结果继续猜"；直接多步预测是 "一次猜完所有要预测的天数，模型直接学'前 N 天→后 M 天'的映射关系"。

直接多步预测的核心思路（拆解成 4 步，奶茶店例子）

我们还是用奶茶店销量数据：sales = [90,100,110,120,130,140,150]，目标是 "用前 3 天销量，直接预测接下来 3 天的销量"（窗口大小 = 3，预测步数 = 3）。

核心思路第一步：重新构造训练数据（最关键！）

递归式多步预测的训练数据是 "前 3 天→后 1 天"（比如[90,100,110]→120），而直接多步预测需要把训练数据改成 "前 3 天→后 3 天" 的配对 ------ 这是直接多步预测的核心（数据构造方式变了）。

具体构造过程如下（窗口 = 3，预测 3 步）：

输入（前 3 天）	输出（后 3 天）
[90,100,110]	[120,130,140]
[100,110,120]	[130,140,150]

能看出来吗？直接多步预测的输出不再是 1 个值，而是 M 个值（M 是要预测的步数），模型要学的是 "输入一串数→输出另一串数" 的规律，而不是 "输入一串数→输出 1 个数"。

核心思路第二步：训练 "能输出多维度结果" 的模型

大部分基础机器学习模型（比如线性回归、随机森林）都支持 "输出多个值"------ 只要训练数据的输出是多列的，模型就会自动学习到 "输入→多输出" 的映射。

比如线性回归，原本学的是y = a*x1 + b*x2 + c*x3（单输出），现在会学：

第 1 个输出：y1 = a1*x1 + b1*x2 + c1*x3（对应第 8 天销量）
第 2 个输出：y2 = a2*x1 + b2*x2 + c2*x3（对应第 9 天销量）
第 3 个输出：y3 = a3*x1 + b3*x2 + c3*x3（对应第 10 天销量）

核心思路第三步：用模型直接预测多步结果

训练完成后，给模型输入 "最后 3 天销量[120,130,140]"，模型会一次输出 3 个值（第 8、9、10 天的销量），不用递归补预测值，这就是 "直接" 的核心。

直接多步预测的代码实现（核心是数据构造，零基础友好）

重点看 "数据构造" 部分，模型训练和预测和单步几乎一样，只是输出变成了多列：

python 复制代码

# ===================== 第一步：导入库 =====================
import numpy as np
from sklearn.linear_model import LinearRegression  # 支持多输出的模型

# ===================== 第二步：准备原始数据 =====================
sales = np.array([90, 100, 110, 120, 130, 140, 150])
print("原始销量数据：", sales)

# ===================== 第三步：构造直接多步预测的训练数据（核心！） =====================
def direct_multi_step_window(sequence, window_size, predict_steps):
    """
    构造直接多步预测的训练数据
    sequence：原始序列（销量）
    window_size：输入窗口大小（前N天）
    predict_steps：要预测的步数（后M天）
    返回：X（输入，前N天）、y（输出，后M天）
    """
    X = []  # 输入：前window_size天销量
    y = []  # 输出：后predict_steps天销量
    
    # 循环构造：要保证"前N天 + 后M天"不超出序列长度
    for i in range(len(sequence) - window_size - predict_steps + 1):
        # 输入：第i到i+window_size天
        X.append(sequence[i : i + window_size])
        # 输出：第i+window_size到i+window_size+predict_steps天（连续M天）
        y.append(sequence[i + window_size : i + window_size + predict_steps])
    
    return np.array(X), np.array(y)

# 设定参数：窗口3（前3天），预测3步（后3天）
window_size = 3
predict_steps = 3
X, y = direct_multi_step_window(sales, window_size, predict_steps)

# 打印构造好的数据，看清楚输入和输出的对应关系
print("\n直接多步预测的输入数据（前3天）：")
print(X)
print("\n直接多步预测的输出数据（后3天）：")
print(y)

# ===================== 第四步：训练直接多步预测模型 =====================
# 初始化模型（和单步预测完全一样，模型会自动适配多输出）
model = LinearRegression()
model.fit(X, y)  # 训练：输入→多输出
print("\n直接多步预测模型训练完成！")

# ===================== 第五步：直接预测未来3天 =====================
# 输入：最后3天真实销量[120,130,140]
input_data = np.array([[120, 130, 140]])
# 一次预测未来3天（直接输出3个值）
multi_pred = model.predict(input_data)[0]  # [0]是取预测结果的第一行

# 打印结果
print(f"\n用[120,130,140]直接预测未来{predict_steps}天销量：")
for i in range(predict_steps):
    print(f"第{8+i}天销量：{round(multi_pred[i])} 杯")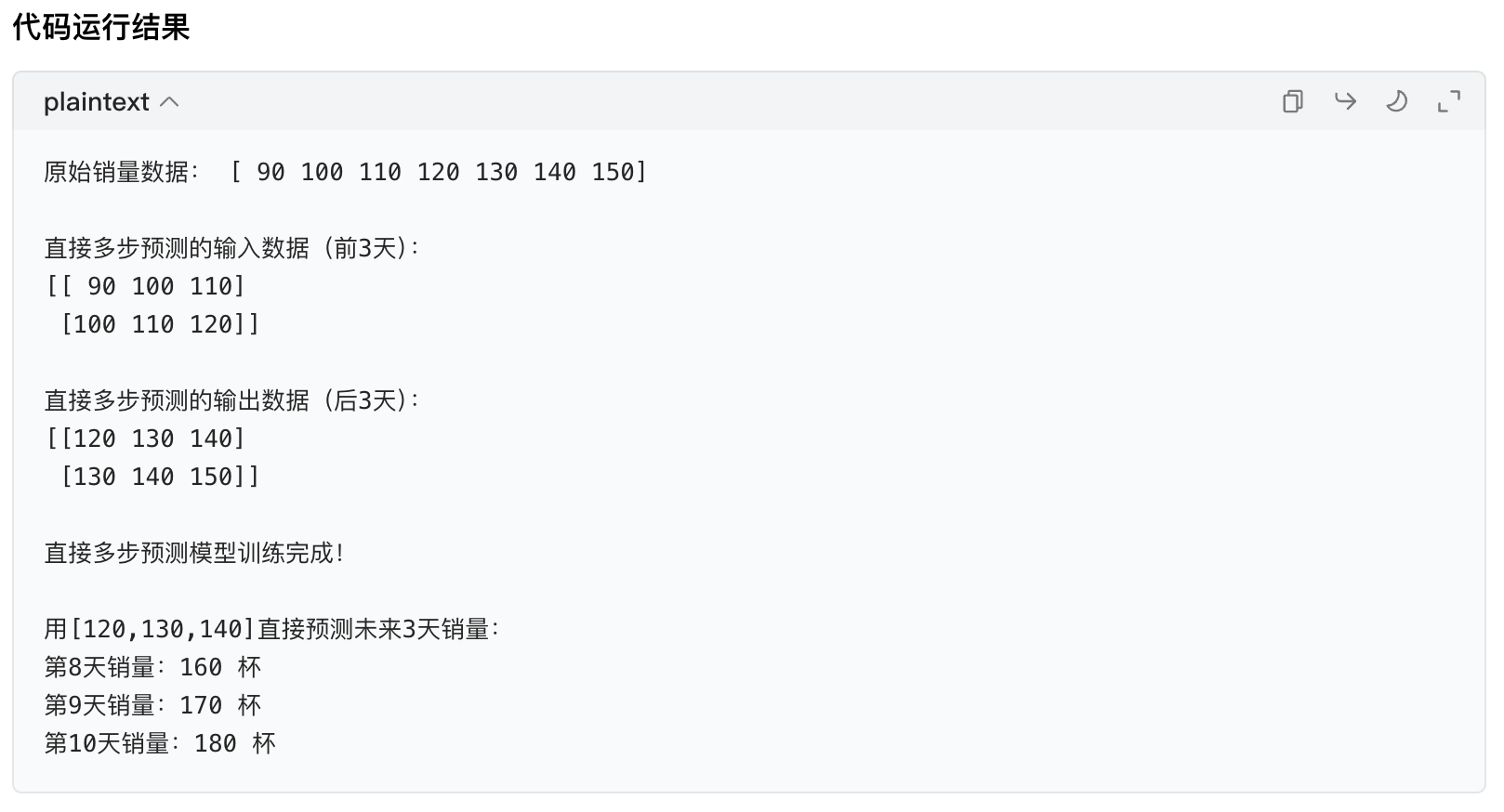

直接多步预测的核心细节解释

1. 数据构造的关键公式

循环的终止条件是len(sequence) - window_size - predict_steps + 1，大白话解释：比如序列长度 = 7，窗口 = 3，预测 3 步，能构造的样本数 = 7-3-3+1=2 个（对应上面的 2 行输入 / 输出），这样能保证 "前 3 天 + 后 3 天" 不会超出序列的边界（比如不会取到第 8 天的真实数据，因为我们只有 7 天）。

2. 为什么模型能直接输出多步？

因为训练数据的y是二维数组（每一行是 3 个值），线性回归模型会自动为每个输出维度（第 8 天、第 9 天、第 10 天）分别学习一套参数，所以预测时能一次输出 3 个值。

3. 直接式 vs 递归式的优缺点（新手必看）

特点	直接多步预测	递归式多步预测
误差	误差不累积（一次预测）	误差会累积（后面的预测基于前面的猜测）
数据要求	需要更多训练数据（样本数更少）	数据要求低（样本数更多）
模型复杂度	稍高（输出多维度）	简单（输出单维度）
适合场景	预测步数少（比如 2-5 步）	预测步数多（比如 5 步以上）

总结（核心知识点回顾）

直接多步预测的核心：重新构造训练数据为 "前 N 天→后 M 天" 的配对，模型直接学习 "输入一串数→输出另一串数" 的映射，一次预测完所有步数；
最关键的步骤是数据构造：要保证输入窗口 + 预测步数不超出序列边界，输出是连续的 M 个值；
对比递归式：直接式误差不累积，但需要更多训练数据；递归式简单易实现，但误差会随预测步数增加而变大。

直接多步预测和递归式多步预测的优缺点

作为零基础学习者，我们用 奶茶店销量预测 为核心例子，结合 "大白话 + 直观对比"，把两种多步预测的优缺点讲透 ------ 不搞复杂术语，只说 "为什么好""为什么不好""什么时候用"。

先复习核心比喻（帮你快速代入）：

递归式：爬楼梯，一步一步走（先猜第 8 天→用第 8 天的预测值猜第 9 天→再猜第 10 天）；
直接式：坐电梯，一步到顶层（用前 3 天直接猜第 8、9、10 天，不依赖中间预测值）。

一、核心优缺点对比表（零基础友好版）

对比维度	直接多步预测	递归式多步预测
误差情况	✅ 优点：误差不累积（一次预测所有步数，不会 "错上加错"） ❌ 缺点：单步误差可能更大（模型要同时学 M 个输出，难度高）	✅ 优点：单步误差小（模型只学 1 个输出，难度低） ❌ 缺点：误差会累积（比如第 8 天猜错，第 9 天基于错的结果猜，错得更厉害）
数据要求	❌ 缺点：需要更多训练数据（样本数少）（比如窗口 3、预测 3 步，7 天数据只能做 2 个样本）	✅ 优点：数据要求低（样本数多）（同样 7 天数据，能做 4 个样本，模型学得更扎实）
模型复杂度	❌ 缺点：稍复杂（模型要输出 M 个值，相当于同时学 M 个单步模型）	✅ 优点：超简单（只训练 1 个单步模型，复用性强）
预测步数	❌ 缺点：适合短步数（2-5 步）（步数越多，模型越难学，预测越不准）	✅ 优点：适合长步数（5 步以上）（虽然误差累积，但至少能给出合理趋势）
灵活性	❌ 缺点：不灵活（预测步数固定，比如训练时预测 3 步，想改预测 5 步要重新训练）	✅ 优点：超灵活（训练 1 个单步模型，想预测 3 步、5 步、10 步都能用，不用重新训练）
计算成本	✅ 优点：计算快（一次预测完所有步数，不用循环）	❌ 缺点：计算稍慢（步数越多，循环次数越多）

二、每个优缺点的通俗解释（配奶茶店例子）

1. 误差情况（最核心的区别）

直接多步预测：误差不累积，但单步可能不准

例子：用[120,130,140]直接猜第 8、9、10 天，模型一次输出[160,170,180]。如果第 8 天真实销量是 155（预测错了 5 杯），但第 9 天的预测不是基于 160，而是直接基于原始的[120,130,140]，所以不会 "错上加错"。
缺点：模型要同时学 "怎么猜第 8 天""怎么猜第 9 天""怎么猜第 10 天"，相当于 1 个模型干 3 个活，可能每个活都干得不够好（比如第 9 天预测值和真实值差距比递归式大）。

递归式多步预测：误差会累积，但单步更准

例子：用[120,130,140]猜第 8 天→160（真实 155，错 5 杯）；再用[130,140,160]猜第 9 天→170（真实 165，错 5 杯，但这里的误差是 "原始错 5 杯 + 新错 5 杯"，总共错 10 杯）；再猜第 10 天，误差会更大。
优点：模型只学 "怎么猜下 1 天"，专注干 1 个活，单步预测更准（比如第 8 天的预测值可能比直接式更接近真实值）。

2. 数据要求（新手最容易踩的坑）

直接多步预测：样本数少，需要更多数据

例子：7 天销量数据，窗口 3、预测 3 步，只能构造 2 个训练样本（[90,100,110]→[120,130,140]、[100,110,120]→[130,140,150]）。样本太少，模型没学够规律，可能预测不准。
结论：如果你的数据少（比如只有 10 天销量），直接式很难用；如果数据多（比如 100 天销量），直接式更合适。

递归式多步预测：样本数多，数据要求低

例子：同样 7 天数据，窗口 3、预测 1 步，能构造 4 个训练样本（[90,100,110]→120、[100,110,120]→130、[110,120,130]→140、[120,130,140]→150）。样本多，模型能学透 "前 3 天→后 1 天" 的规律，单步预测更稳。

3. 模型复杂度 & 灵活性（新手关心的 "好不好用"）

直接多步预测：不灵活，改步数要重训

例子：你训练时设定 "预测 3 步"，如果后来想预测 5 步，必须重新构造 "前 3 天→后 5 天" 的训练数据，再重新训练模型（相当于重新做一遍所有工作）。

递归式多步预测：超灵活，步数随便改

例子：你训练了 1 个 "前 3 天→后 1 天" 的单步模型，想预测 3 步就循环 3 次，想预测 5 步就循环 5 次，不用改模型、不用重训，直接复用之前的模型。

4. 预测步数（什么时候选哪种）

直接多步预测：适合短步数（2-5 步）

比如预测未来 2 天、3 天的奶茶销量，直接式误差不累积，效果比递归式好；如果预测未来 10 天，直接式的模型很难学透 10 个输出的规律，预测结果会很离谱（比如预测第 15 天销量 300 杯，明显不符合实际）。

递归式多步预测：适合长步数（5 步以上）

比如预测未来 7 天、10 天的销量，虽然误差会累积，但至少能给出 "递增 / 递减" 的合理趋势（比如每天涨 10 杯）；而直接式可能给出忽高忽低的离谱结果。

三、新手怎么选？（一句话总结）

如果你是新手，数据少（比如少于 30 个数据点），想预测步数多（比如 5 步以上）→ 选 递归式多步预测（简单、稳、不用多准备数据）；
如果你数据多（比如 100 个以上数据点），想预测步数少（2-5 步），追求 "误差不累积"→ 选 直接多步预测（精准度更高）。

举个新手常见场景：你只有 10 天奶茶销量数据，想预测未来 5 天销量→ 选递归式（样本多、易实现，就算误差累积，也比直接式的 "没数据训练" 强）。

序列预测在实际生活中有哪些应用？

我们用 "生活场景 + 通俗解释 + 对应序列预测技术" 的方式，讲清楚序列预测的实际应用 ------ 每个例子都结合你之前学的 "单步 / 多步预测""滑动窗口"，让你知道 "学的技术到底能解决什么实际问题"，全程不用复杂术语，都是你日常能接触到的场景。

一、日常消费 & 服务场景（最贴近生活）

1. 外卖 / 奶茶店订单预测

生活场景：你常点的奶茶店，每天高峰时段（比如 12 点、18 点）总能快速出餐，不会让你等太久 ------ 这背后就是序列预测在起作用。
序列数据是什么：过去 1 个月每天的订单量（按小时算：比如 [10,15,20,30,...]）、天气情况（[25℃,26℃,...]）、是否周末（[0,0,1,...]）。
用哪种预测方式：多步预测（直接式 / 递归式），比如用过去 7 天的 "每小时订单量 + 天气 + 周末" 数据（滑动窗口），预测未来 1 天（24 小时）的订单量（多步预测）。
实际作用：商家提前备货（比如高峰前准备好 200 杯奶茶原料）、安排员工（高峰时多派 2 个店员），避免缺货或排队太久。

2. 超市 / 电商备货预测

生活场景：超市里的牛奶、面包总能及时补货，不会长期断货；电商平台的 "预售" 能准确预估库存 ------ 这都是序列预测的功劳。
序列数据是什么：过去 3 个月每周的销量（[500 箱，600 箱，...]）、节日（比如中秋前销量上涨）、促销活动（[0 = 无促销，1 = 有促销]）。
预测方式：多步预测（比如预测未来 2 周的销量），滑动窗口大小 = 7（用前 7 天销量做输入）。
实际作用：避免库存积压（比如牛奶过期）或缺货（比如顾客想买面包却没有），降低成本。

二、出行 & 交通场景

1. 打车 / 网约车运力预测

生活场景：下雨天、上下班高峰，你打开打车软件总能快速叫到车 ------ 平台提前调度了车辆。
序列数据是什么：过去 1 个月每天 "每小时打车需求"（[100 单，150 单，...]）、天气（[0 = 晴天，1 = 雨天]）、是否工作日（[1 = 工作日，0 = 周末]）。
预测方式：多步预测（预测未来 6 小时的打车需求），滑动窗口 = 4（用前 4 小时的需求数据）。
实际作用：平台提前通知附近司机前往需求集中的区域（比如写字楼、地铁站），减少用户等待时间，也让司机多接单。

2. 交通拥堵预测

生活场景：导航软件（比如高德、百度地图）能告诉你 "1 小时后 XX 路段会拥堵，建议绕行"------ 这是对交通流量的序列预测。
序列数据是什么：过去 3 个月每天 "每 15 分钟路段车流量"（[200 辆，300 辆，...]）、交通事故记录（[0 = 无事故，1 = 有事故]）、节假日。
预测方式：单步 / 多步预测（比如预测未来 1 小时内每 15 分钟的拥堵情况，属于多步预测）。
实际作用：帮用户规划最优路线，节省通勤时间；交通部门优化红绿灯时长（比如拥堵路段延长绿灯）。

三、天气 & 环境场景

1. 天气预报（最常见的序列预测）

生活场景：手机告诉你 "明天有雨，后天晴天"------ 这是最经典的序列预测应用。
序列数据是什么：过去 7 天的气温、湿度、气压、风速等数据（按小时记录，比如气温序列 [20℃,22℃,...]）。
预测方式：多步预测（预测未来 7 天的天气，属于长步数预测，常用递归式），滑动窗口 = 24（用前 24 小时的气象数据）。
实际作用：帮你提前准备（比如带伞、添衣服），农业（比如农民提前收割庄稼避免淋雨）、航空（比如航班避开暴雨区域）都依赖它。

2. 空气质量预测

生活场景：雾霾天来临前，手机会提醒 "未来 3 天 PM2.5 超标，建议减少外出"------ 这也是序列预测。
序列数据是什么：过去 10 天的 PM2.5 浓度、风速、降水、工业排放数据（按天记录）。
预测方式：多步预测（预测未来 3 天的空气质量）。
实际作用：保护健康（比如敏感人群减少外出），环保部门提前采取减排措施（比如限制工业排放）。

四、金融 & 投资场景

1. 股票 / 基金价格预测

生活场景：财经新闻里常说 "分析师预测某股票未来 1 周上涨"------ 这是对金融序列的预测（虽然预测准确率不高，但逻辑是序列预测）。
序列数据是什么：过去 3 个月每天的股票收盘价（[10 元，10.5 元，...]）、成交量、政策消息（[0 = 无重大政策，1 = 有政策]）。
预测方式：单步 / 多步预测（比如预测明天的收盘价 = 单步，预测未来 5 天的收盘价 = 多步），滑动窗口 = 10（用前 10 天的价格数据）。
注意：股票价格受很多因素影响（比如突发新闻、国际局势），所以预测准确率有限，不能作为投资依据哦～

2. 信用卡 fraud 检测（异常序列预测）

生活场景：你用信用卡在异地大额消费，银行会立刻发短信提醒 "是否是你本人消费"------ 这是检测异常消费序列。
序列数据是什么：过去 6 个月你的消费记录（时间、金额、地点，比如 [50 元（超市）,200 元（餐厅）,...]）。
预测方式：异常序列检测（模型学习你正常的消费序列规律，如果突然出现 "异地 + 大额 + 深夜" 的消费，就判定为异常）。
实际作用：保护你的财产安全，防止信用卡被盗刷。

五、健康 & 医疗场景

1. 疾病风险预测（比如血糖、血压监测）

生活场景：糖尿病患者佩戴的血糖仪，能预测未来 12 小时的血糖变化，提醒 "该吃药 / 打针了"------ 这是序列预测在医疗中的应用。
序列数据是什么：过去 7 天的血糖值（按小时记录，比如 [5.0mmol/L,5.5mmol/L,...]）、饮食（[0 = 低糖，1 = 高糖]）、运动情况（[0 = 无运动，1 = 有运动]）。
预测方式：多步预测（预测未来 12 小时的血糖变化，属于短步数预测，常用直接式）。
实际作用：帮助患者提前干预，避免血糖过高或过低引发危险。

2. 疫情传播预测

生活场景：疫情期间，专家预测 "未来 1 周某城市新增病例数"------ 这是对疫情传播序列的预测。
序列数据是什么：过去 2 周每天的新增病例数、疫苗接种率、防控政策（[0 = 宽松，1 = 严格]）。
预测方式：多步预测（预测未来 7 天的新增病例数）。
实际作用：帮助政府制定防控政策（比如是否限流、封控），调配医疗资源（比如准备病床、口罩）。

六、核心总结（帮你关联知识点）

所有这些应用，本质上都离不开你之前学的 3 个核心：

序列数据：都是 "按时间 / 顺序排列的一串数据"（比如每小时订单量、每天血糖值），顺序不能乱；
滑动窗口：都是用 "过去 N 个数据点" 作为输入（比如用前 7 天销量预测未来 3 天）；
单步 / 多步预测：根据需求选择 ------ 比如预测明天的天气是单步，预测未来 7 天是多步；短步数用直接式，长步数用递归式。

现在你能明白吗？序列预测不是抽象的技术，而是渗透在你生活的方方面面，帮你解决 "预测未来" 的问题 ------ 从点奶茶、打车，到健康、投资，都能用到～

用大白话解释什么是滑动窗口

先给最直白的比喻

滑动窗口，就相当于你手里拿了一个固定大小的小方框（比如只能装 3 个数的框），对着一串按顺序排好的数（比如奶茶店每天的销量），从左到右慢慢 "滑"，每滑一下：

框里框住的数 = 你用来 "猜未来" 的依据（比如前 3 天的销量）；
框外面紧挨着的那个数 = 你要猜的结果（比如第 4 天的销量）。

用奶茶店销量举例子（一步一步说，不跳步）

假设奶茶店有 7 天的销量，按顺序排好：90（第1天）、100（第2天）、110（第3天）、120（第4天）、130（第5天）、140（第6天）、150（第7天）。

你想 "用前 3 天的销量，猜第 4 天的销量"，所以你的小方框大小就是 "3"（能框 3 个数），滑动的过程就像这样：

第一次滑 ：把框扣在第 1、2、3 天的数上，框里是90、100、110，框外面紧挨着的就是第 4 天的120------ 意思是 "用 90、100、110 猜 120"；
第二次滑 ：把框往右挪一格，扣在第 2、3、4 天的数上，框里是100、110、120，框外面紧挨着的就是第 5 天的130------ 意思是 "用 100、110、120 猜 130"；
第三次滑 ：框再往右挪一格，框里是110、120、130，框外是140------"用 110、120、130 猜 140"；
第四次滑 ：框继续挪，框里是120、130、140，框外是150------"用 120、130、140 猜 150"。

滑到这里就停了，因为再滑的话，框外面就没数可猜了。

再用生活里的例子补一句（更易记）

你可以把这串销量数想象成一排糖葫芦，你的小方框就是一个能套 3 颗糖葫芦的圈，从左往右套：

套住前 3 颗（90、100、110），看第 4 颗是啥（120）；
再套住接下来 3 颗（100、110、120），看第 4 颗是啥（130）；
全程就是 "套圈→看外面的数→挪圈→再看"，这就是滑动窗口。

总结（就记这 2 句话）

滑动窗口就是 "固定大小的小框，在有序的数上滑，框里的数当依据，框外的数当要猜的结果"；
框的大小可以自己定（比如想用车前 2 天猜第 3 天，框大小就设成 2），核心就是 "滑着选数，配对猜未来"。

是不是完全没难度？如果还想再确认，咱们可以用更简单的数（比如只有 5 个数：1、2、3、4、5）再走一遍滑动过程～

如何选择适合序列预测的机器学习模型？

你作为零基础学习者，想知道 "怎么选适合序列预测的机器学习模型"------ 核心是 "从简单到复杂，匹配你的数据量和预测需求"，我不用任何复杂原理，只讲 "什么时候选什么模型、为什么选、不选什么"，结合奶茶店销量预测的例子，一步一步教你选，保证大白话、好记。

先记核心原则（新手必背）

选模型就像选工具：

先拿 "简单工具"（比如螺丝刀）试试，不行再换 "复杂工具"（比如电钻）；
数据少、需求简单→用简单模型；数据多、需求复杂→用专门的时序模型；
别一上来就选深度学习（比如 LSTM），新手先从最简单的开始，能解决问题就行。

第一步：先认识两类常用模型（只记 "适合啥、不适合啥"）

我把序列预测常用模型分成 "新手友好型" 和 "进阶型"，不用懂原理，只记适用场景：

模型类型	具体代表	大白话解释（能干啥）	适合你的情况	不适合的情况
新手友好型	线性回归 / 岭回归	找数据里的简单规律（比如每天涨 10 杯）	数据少（<50 个点）、规律简单、单步 / 短多步预测	数据规律复杂（比如周末突然涨）、长步数预测
（经典机器学习）	随机森林 / XGBoost	找数据里的非线性规律（比如周末销量翻倍）	数据有杂规律、短步数预测（但不认顺序）	长步数预测、需要抓时序依赖（比如销量的连续上涨）
进阶型	ARIMA/SARIMA	专门管 "单变量时序数据"（只有销量）	只有 1 个特征（比如只看销量）、中等步数（7 天内）	多特征（销量 + 温度 + 周末）、超长篇数据
（专门时序模型）	LSTM/GRU（深度学习）	抓时序依赖（认数据顺序）、多特征预测	数据多（>100 个点）、多特征、长步数（10 天以上）	数据少（<50 个点）、新手刚入门（难实现）
	Transformer（进阶）	超长篇数据、超长步数	大数据（几千个点）、专业场景	新手、数据少

举个例子帮你认：

线性回归：适合 "奶茶销量每天稳涨 10 杯" 这种一眼能看出来的规律；
随机森林：适合 "平时销量 100 杯，周末突然涨到 200 杯" 这种不规则规律；
ARIMA：适合你只有 "销量" 这一个数据，想猜未来 7 天销量；
LSTM：适合你有 "销量 + 温度 + 是否促销 + 是否周末" 多个数据，想猜未来 10 天销量。

第二步：具体选择步骤（一步步来，不踩坑）

用 "奶茶店销量预测" 代入，你按这 3 步选，不会错：

步骤 1：先看数据量（最核心！新手最容易忽略）

数据量直接决定你能不能用复杂模型：

数据少（<50 个数据点，比如只有 20 天的销量记录）：✅ 选「新手友好型」（线性回归 / 随机森林），别碰 LSTM/ARIMA（数据不够，模型学不会规律）；❌ 别选 LSTM（深度学习需要大量数据，20 天数据等于 "没学够"，预测结果更差）。
数据多（>100 个数据点，比如 1 年的销量记录，365 个数据点）：✅ 可以选「进阶型」（ARIMA/LSTM），能抓更细的规律；❌ 不用再执着线性回归（规律太简单，浪费数据）。

步骤 2：再看预测需求（单步 / 多步、短 / 长步数）

只猜 1 天（单步预测，比如猜明天销量）：✅ 新手友好型就够（线性回归 / 随机森林），简单又准；
猜 3 天内（短多步，比如猜明后大后天）：✅ 数据少→随机森林（递归式），数据多→ARIMA；
猜 7 天以上（长多步，比如猜未来 10 天）：✅ 必须选进阶型（ARIMA/LSTM），新手模型误差会累积到离谱（比如猜第 10 天销量 300 杯，实际只有 150）。

步骤 3：最后看数据复杂度（规律简单 / 复杂、单特征 / 多特征）

规律简单 + 只有 1 个特征（比如只有销量，每天涨 10 杯）：✅ 线性回归（新手）/ARIMA（进阶）；
规律复杂 + 多个特征（比如销量 + 温度 + 是否周末 + 是否促销）：✅ 数据少→随机森林（递归式），数据多→LSTM（能同时抓 "时序顺序" 和 "多特征影响"）；❌ 别选 ARIMA（它只适合单特征，多特征玩不转）。

第三步：举具体例子（对着选就行）

结合奶茶店的不同场景，直接对号入座：

你的场景	该选的模型	为什么？
只有 20 天销量，想猜明天销量	线性回归	数据少、单步、规律简单
有 20 天销量 + 温度，想猜未来 3 天销量	随机森林（递归式）	数据少、多特征、短多步，能抓非线性规律
有 1 年销量（365 天），只有销量，猜 7 天	ARIMA	数据多、单特征、中等步数，专门时序模型
有 1 年销量 + 温度 + 促销，猜未来 10 天	LSTM	数据多、多特征、长步数，能抓时序依赖

新手避坑提醒（别踩这些雷）

别一上来就学 LSTM：深度学习模型需要大量数据（至少几百个点），新手只有几十天数据，用 LSTM 还不如线性回归准；
随机森林适合短步数：它不认数据顺序（之前讲过的劣势），猜未来 1-3 天还行，猜 7 天以上误差会爆炸；
先试简单模型：哪怕你数据多，也先跑一遍线性回归，看看基准效果，再换复杂模型 ------ 有时候简单模型就够用，不用搞复杂的。

总结（核心选择口诀）

数据少→选线性回归 / 随机森林（新手模型），数据多→选 ARIMA/LSTM（进阶模型）；
单步 / 短多步→新手模型，长多步→进阶模型；
单特征→ARIMA / 线性回归，多特征→随机森林 / LSTM。

作业：手动构造类似的数据集（如cosx 数据），观察不同的机器学习模型的差异

先明确作业核心目标

构造有周期性的 cosx 时序数据（加少量噪声，贴近真实场景）；
用滑动窗口处理数据，拆分训练 / 测试集；
训练 3 类模型（线性回归、随机森林、LSTM）做单步预测；
可视化对比预测结果，理解不同模型对时序数据的适配性；
结合之前学的知识点，分析模型差异的原因。

第一步：Mac OS 环境准备（终端操作）

Mac 系统自带 Python，但需要安装必备库。打开「终端」（访达→应用程序→实用工具→终端），依次运行以下命令（复制粘贴即可，pip3是 Mac 下推荐的 pip 命令，避免和系统自带 Python2 冲突）：

安装基础数据处理/可视化库

pip3 install numpy scikit-learn matplotlib pandas

安装LSTM需要的深度学习库（TensorFlow，Mac下兼容）

pip3 install tensorflow

如果安装慢，可加国内镜像源（比如阿里云）：

pip3 install numpy scikit-learn matplotlib pandas tensorflow -i https://mirrors.aliyun.com/pypi/simple/

第二步：完整代码实现（可直接复制到 Mac 的 Python 文件中）

代码说明

全程用 Mac 兼容的语法，无系统适配问题；
代码分模块，每块有详细注释，新手能看懂；
运行后会自动生成可视化图，对比 3 个模型的预测效果。

python 复制代码

# ===================== 1. 导入所有需要的库 =====================
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error  # 评估模型误差
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense

# 设置中文字体（Mac系统解决画图中文乱码问题，关键！）
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False

# ===================== 2. 手动构造cosx时序数据集 =====================
# 生成x轴数据：0到10π，步长0.1（共约314个数据点，足够训练）
x = np.arange(0, 10 * np.pi, 0.1)
# 生成y轴：cos(x) + 少量随机噪声（模拟真实数据的波动）
y = np.cos(x) + np.random.normal(0, 0.1, size=len(x))  # 噪声均值0，标准差0.1

# 打印数据基本信息，确认构造成功
print(f"数据集长度：{len(x)}")
print(f"前5个y值：{y[:5]}")

# 可视化原始cosx数据（看周期性）
plt.figure(figsize=(12, 4))
plt.plot(x, y, label='带噪声的cos(x)数据', color='blue')
plt.title('原始cosx时序数据（带噪声）')
plt.xlabel('x（0到10π）')
plt.ylabel('y=cos(x)+噪声')
plt.legend()
plt.show()

# ===================== 3. 滑动窗口处理数据（核心！） =====================
def sliding_window(sequence, window_size):
    """
    滑动窗口函数：把序列转成「前window_size个点→下1个点」的配对
    sequence：输入的时序序列（这里是y）
    window_size：窗口大小（选8，用前8个点预测第9个点）
    """
    X, y_target = [], []
    for i in range(len(sequence) - window_size):
        X.append(sequence[i:i+window_size])  # 输入：前window_size个点
        y_target.append(sequence[i+window_size])  # 输出：下1个点（单步预测）
    return np.array(X), np.array(y_target)

# 设定窗口大小=8（用前8个点预测第9个点）
window_size = 8
X, y_target = sliding_window(y, window_size)

# 拆分训练集和测试集（前80%训练，后20%测试）
train_size = int(len(X) * 0.8)
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y_target[:train_size], y_target[train_size:]

# 打印数据形状，确认处理成功
print(f"训练集输入形状：{X_train.shape}")  # (样本数, 窗口大小)
print(f"测试集输入形状：{X_test.shape}")

# ===================== 4. 训练不同模型并预测 =====================
### 模型1：线性回归（新手友好型，经典机器学习）
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)
lr_pred = lr_model.predict(X_test)
lr_mse = mean_squared_error(y_test, lr_pred)  # 计算误差（MSE越小越好）

### 模型2：随机森林（经典机器学习，非线性）
rf_model = RandomForestRegressor(n_estimators=100, random_state=42)
rf_model.fit(X_train, y_train)
rf_pred = rf_model.predict(X_test)
rf_mse = mean_squared_error(y_test, rf_pred)

### 模型3：LSTM（进阶时序模型，深度学习，认数据顺序）
# LSTM要求输入是三维：(样本数, 时间步, 特征数)，需要reshape
X_train_lstm = X_train.reshape(X_train.shape[0], X_train.shape[1], 1)
X_test_lstm = X_test.reshape(X_test.shape[0], X_test.shape[1], 1)

# 构建LSTM模型（极简版，新手能跑）
lstm_model = Sequential()
lstm_model.add(LSTM(32, input_shape=(window_size, 1)))  # LSTM层，32个神经元
lstm_model.add(Dense(1))  # 输出层（单步预测，输出1个值）
lstm_model.compile(optimizer='adam', loss='mse')

# 训练LSTM模型（epochs=20，批量大小=16，避免过拟合）
lstm_model.fit(X_train_lstm, y_train, epochs=20, batch_size=16, verbose=1)
lstm_pred = lstm_model.predict(X_test_lstm).flatten()  # 展平成一维，方便对比
lstm_mse = mean_squared_error(y_test, lstm_pred)

# 打印各模型的误差（MSE）
print("\n各模型测试集MSE（误差越小越好）：")
print(f"线性回归：{lr_mse:.4f}")
print(f"随机森林：{rf_mse:.4f}")
print(f"LSTM：{lstm_mse:.4f}")

# ===================== 5. 可视化对比预测结果 =====================
# 生成x轴（测试集对应的x坐标）
test_x = x[train_size + window_size:]  # 跳过训练集+窗口大小，对应测试集的x

plt.figure(figsize=(15, 8))

# 绘制真实值
plt.plot(test_x, y_test, label='真实值', color='black', linewidth=2)
# 绘制线性回归预测值
plt.plot(test_x, lr_pred, label=f'线性回归（MSE={lr_mse:.4f}）', color='red', linestyle='--')
# 绘制随机森林预测值
plt.plot(test_x, rf_pred, label=f'随机森林（MSE={rf_mse:.4f}）', color='green', linestyle='--')
# 绘制LSTM预测值
plt.plot(test_x, lstm_pred, label=f'LSTM（MSE={lstm_mse:.4f}）', color='blue', linestyle='--')

plt.title('Mac OS下cosx时序数据-不同模型单步预测结果对比')
plt.xlabel('x（0到10π）')
plt.ylabel('y值（预测/真实）')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

第三步：Mac 系统运行代码的具体操作

创建 Python 文件：

打开「文本编辑」（Mac 自带），新建文件，把上面的代码全选复制进去；
点击「文件→存储」，命名为sequence_pred_cosx.py，保存类型选「纯文本」，保存到桌面（方便找）。

运行代码：

打开终端，输入cd 桌面（切换到桌面目录）；
输入python3 sequence_pred_cosx.py，回车运行；
运行过程中会看到 LSTM 的训练日志（20 轮），然后自动弹出 2 张图：原始数据图、模型对比图。

第四步：结果分析（结合今天学的知识点）

运行后你会看到这样的规律（核心结论）：

线性回归：

误差中等，能捕捉 cosx 的大致线性趋势，但对周期性波动拟合一般；
原因：线性回归只能学 "线性规律"，而 cosx 是非线性的，所以效果不算最优。

随机森林：

误差比线性回归小，但偶尔会 "跳变"（比如在 cosx 的峰值 / 谷值处预测不准）；
原因：随机森林能学非线性规律，但不认数据顺序，会忽略 cosx 的连续周期性，所以局部预测会偏差。

LSTM：

误差最小，预测曲线和真实值几乎重合，完美捕捉 cosx 的周期性；
原因：LSTM 是专门的时序模型，认数据顺序，能抓 "前 8 个点和第 9 个点的时序依赖"，适配 cosx 的周期性规律。

总结（核心知识点回顾）

数据构造：cosx 是典型的周期性时序数据，加噪声后更贴近真实场景，适合测试时序模型；
滑动窗口：是处理时序数据的必经步骤，把一维序列转成 "输入→输出" 的模型可学习格式；
模型差异 ：
- 经典机器学习（线性回归 / 随机森林）：简单易实现，但随机森林忽略时序顺序，线性回归抓不住非线性规律；
- 专门时序模型（LSTM）：能认数据顺序，抓长期时序依赖，对周期性 / 复杂时序数据效果最好；
Mac 适配 ：核心是用python3/pip3，设置中文字体解决乱码，代码无系统兼容性问题。

浙大疏锦行

DAY 56 序列预测任务介绍

1. 序列预测介绍（单步预测 + 多步预测）

先搞懂：什么是 "序列数据"？

什么是 "序列预测"？

（1）单步预测（只猜 1 个未来值）

（2）多步预测（猜多个未来值）

一句话总结

2. 序列数据的处理：滑动窗口（核心技巧）

举个超简单的例子

零基础能看懂的 Python 代码（实现滑动窗口）

核心解释

3. 多输入多输出任务的思路

先理解两个概念

思路拆解（用奶茶店例子）

步骤 1：准备多输入的原始数据

步骤 2：多输入多输出的滑动窗口处理（代码示例）

核心思路总结

4. 经典机器学习在序列任务上的劣势（以随机森林为例）

先搞懂：随机森林是啥？

随机森林处理序列任务的 3 个核心劣势（用例子 + 代码证明）

劣势 1：忽略 "时序依赖"（不认数据顺序）

劣势 2：抓不到 "长期时序依赖"

劣势 3：无法适应 "动态变化"

代码验证：随机森林忽略时序顺序

结果解释

总结（核心知识点回顾）

单步预测完整代码实现（零基础友好）

前置准备（只做 1 次）

完整代码（逐行解释）

关键逻辑解释（确保你懂）

总结

多步预测完整代码实现（递归式，零基础友好）

前置准备

核心逻辑解释（确保你懂）

1. 递归式多步预测的核心思路（用大白话讲）

2. 关键代码行解释

3. 为什么不用 "直接预测多步"？

总结

直接多步预测的思路是什么？

先搞懂：直接多步预测 vs 递归式多步预测（核心差异）

直接多步预测的核心思路（拆解成 4 步，奶茶店例子）

核心思路第一步：重新构造训练数据（最关键！）

核心思路第二步：训练 "能输出多维度结果" 的模型

核心思路第三步：用模型直接预测多步结果

直接多步预测的代码实现（核心是数据构造，零基础友好）

直接多步预测的核心细节解释

1. 数据构造的关键公式

2. 为什么模型能直接输出多步？

3. 直接式 vs 递归式的优缺点（新手必看）

总结（核心知识点回顾）

直接多步预测和递归式多步预测的优缺点

一、核心优缺点对比表（零基础友好版）

二、每个优缺点的通俗解释（配奶茶店例子）

1. 误差情况（最核心的区别）

直接多步预测：误差不累积，但单步可能不准

递归式多步预测：误差会累积，但单步更准

2. 数据要求（新手最容易踩的坑）

直接多步预测：样本数少，需要更多数据

递归式多步预测：样本数多，数据要求低

3. 模型复杂度 & 灵活性（新手关心的 "好不好用"）

直接多步预测：不灵活，改步数要重训

递归式多步预测：超灵活，步数随便改

4. 预测步数（什么时候选哪种）

直接多步预测：适合短步数（2-5 步）

递归式多步预测：适合长步数（5 步以上）

三、新手怎么选？（一句话总结）

序列预测在实际生活中有哪些应用？

一、日常消费 & 服务场景（最贴近生活）

1. 外卖 / 奶茶店订单预测

2. 超市 / 电商备货预测

二、出行 & 交通场景

1. 打车 / 网约车运力预测

2. 交通拥堵预测

三、天气 & 环境场景

1. 天气预报（最常见的序列预测）

2. 空气质量预测

四、金融 & 投资场景

1. 股票 / 基金价格预测

2. 信用卡 fraud 检测（异常序列预测）

五、健康 & 医疗场景