
使用 push_back 的优点:
-
动态扩容:不需要预先知道结果的数量
-
方便快捷:一行代码完成添加操作
-
性能良好 :
push_back的平均时间复杂度是 O(1)
功能:
-
将一个新元素添加到
vector的末尾 -
自动调整
vector的大小(容量可能会增加)
cpp
vector<int> nums;
nums.push_back(10); // nums 变为 [10]
nums.push_back(20); // nums 变为 [10, 20]
nums.push_back(30); // nums 变为 [10, 20, 30]
cpp
暴力解法
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
// 存储结果的容器,用于保存每个滑动窗口的最大值
vector<int> result;
// 处理边界情况:
// 1. 如果数组为空,直接返回空结果
// 2. 如果k小于等于0,窗口大小不合法
// 3. 如果k大于数组长度,窗口无法形成
if (nums.empty() || k <= 0 || k > nums.size()) {
return result; // 返回空结果
}
// 外层循环:遍历所有可能的窗口起始位置
// i表示窗口的起始索引,从0开始到nums.size()-k结束
// 例如:数组长度为8,k=3,则i的取值范围是0~5
for (int i = 0; i <= nums.size() - k; ++i) {
// 初始化当前窗口的最大值为窗口的第一个元素
// maxVal用于记录当前窗口找到的最大值
int maxVal = nums[i];
// 内层循环:遍历当前窗口内的所有元素
// j从窗口起始位置i开始,到窗口结束位置i+k-1结束
// 例如:i=0, k=3时,j遍历0,1,2三个位置
for (int j = i; j <= i + k - 1; ++j) {
// 更新当前窗口的最大值
// 如果当前元素nums[j]大于当前记录的最大值maxVal
if (nums[j] > maxVal) {
// 更新maxVal为更大的值
maxVal = nums[j];
}
// 注意:这里没有else,因为如果nums[j] <= maxVal,保持maxVal不变
}
// 内层循环结束后,maxVal就是当前窗口的最大值
// 将当前窗口的最大值添加到结果容器中
result.push_back(maxVal);
}
// 所有窗口处理完毕,返回包含所有窗口最大值的数组
return result;
}
};方法二

cpp
class Solution {
private:
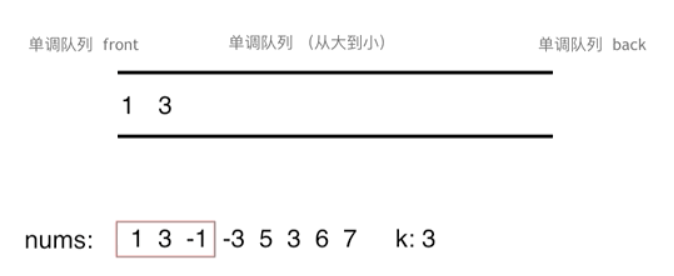
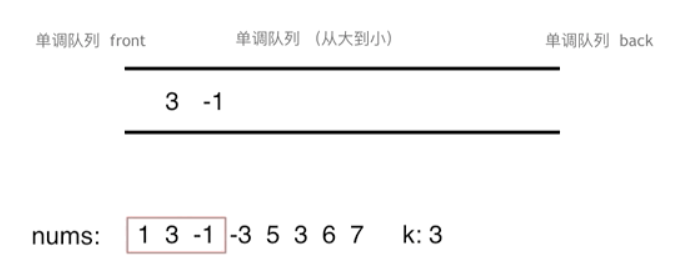
class MyQueue { //单调队列(从大到小)MyQueue是实现滑动窗口最大值算法的辅助数据结构,它专为Solution类的需求而设计,只在Solution内部使用,不是通用的队列,外部不需要知道或访问这个内部类
cpp
class Solution {
private:
// 自定义单调队列类(内部元素单调递减,队头最大)
class MyQueue {
public:
deque<int> que; // 使用双端队列作为底层容器,支持两端高效插入删除
// 弹出元素:只有当要弹出的值等于当前队头(最大值)时才真正弹出队头
void pop(int value) {
// 若队列非空且当前要移除的元素就是队头元素(即窗口滑动移出的元素是当前最大值)
if (!que.empty() && value == que.front()) {
que.pop_front(); // 弹出队头
}
// 否则说明要移出的元素不是当前最大值,已在之前被覆盖弹出,无需操作
}
// 插入元素:维护队列的单调递减性
void push(int value) {
// 当队列非空且新元素大于队尾元素时,不断弹出队尾元素
// 这样可以确保队列始终保持从队头到队尾的递减顺序
while (!que.empty() && value > que.back()) {
que.pop_back(); // 弹出队尾,直到新元素找到合适位置
}
que.push_back(value); // 将新元素插入队尾
}
// 获取当前队列最大值(即队头元素)
int front() {
return que.front();
}
};
public:
// 主函数:滑动窗口最大值
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
MyQueue que; // 创建单调队列实例
vector<int> result; // 存储结果的数组
// 初始化:将第一个窗口的k个元素加入队列
for (int i = 0; i < k; i++) {
que.push(nums[i]); // 插入元素时会自动维护单调性
}
// 第一个窗口的最大值就是当前队头
result.push_back(que.front());
// 从第k个元素开始,滑动窗口
for (int i = k; i < nums.size(); i++) {
// 窗口向右移动,移除窗口最左侧元素(i-k为移出元素的索引)
que.pop(nums[i - k]);
// 将新进入窗口的元素加入队列(i为当前新元素的索引)
que.push(nums[i]);
// 当前窗口的最大值即为队头元素
result.push_back(que.front());
}
return result; // 返回所有窗口的最大值集合
}
};方法三
cpp
cpp
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
map<int,int> mp;
vector<int> result;
int size=nums.size();
int left=0,right=k-1;
for(int i=0;i<=k-1;i++) mp[nums[i]]++;
while(right<size){
result.push_back(mp.rbegin()->first);
left++;
right++;
if(right>=size) break;
mp[nums[right]]++;
mp[nums[left-1]]--;
while(mp.rbegin()->second==0) mp.erase(mp.rbegin()->first);
}
return result;
}
};