目录
- 一、题目
- 二、分析
-
-
- 一)匈牙利算法的适用场景
- 二)匈牙利算法的核心原理
- 三)匈牙利算法的步骤
-
- 步骤1:行约减------每行减该行最小值
- 步骤2:列约减------每列减该列最小值
- 步骤3:用最少的直线覆盖所有0元素
- [步骤4:构造新的0元素(当 k < n 时)](#步骤4:构造新的0元素(当 k < n 时))
- [步骤 5:寻找独立的 0 元素(最优匹配)](#步骤 5:寻找独立的 0 元素(最优匹配))
- 匈牙利算法总结
-
- 三、求解
- 四、代码
一、题目

二、分析
指派问题(Assignment Problem)属于组合优化中的经典问题,这里采用最简洁高效的求解算法匈牙利算法(Hungarian Algorithm)。
指派问题的核心是:将 n 个任务分配给 n 个人,每人做1个任务,每个任务仅分配1人,求总成本最小(或最大)的方案。
匈牙利算法专门针对这类二分图匹配的最小权问题,时间复杂度为 (O(n^3)),比暴力枚举((O(n!)))高效得多,尤其适合 (n) 较小的场景。
一)匈牙利算法的适用场景
专门解决 指派问题(Assignment Problem):
- 有 n n n 个"执行者"和 n n n 个"任务";
- 每个执行者只能做1个任务,每个任务只能被1个执行者做;
- 已知执行者 i i i做任务 j j j 的成本为 c [ i ] [ j ] c[i][j] c[i][j];
- 目标:找到总成本最小的分配方案,也可扩展到"最大化收益",只需将收益取负转化为成本。
二)匈牙利算法的核心原理
匈牙利算法是专门解决指派问题 的经典算法,通过矩阵约减 (行/列减最小值),让矩阵中出现尽可能多的"0元素",最终找到 n n n个"独立的0元素"(即每个行、列仅包含1个0)------这些0对应的分配方案,就是总成本最小的方案。
三)匈牙利算法的步骤
成本矩阵(n=3)
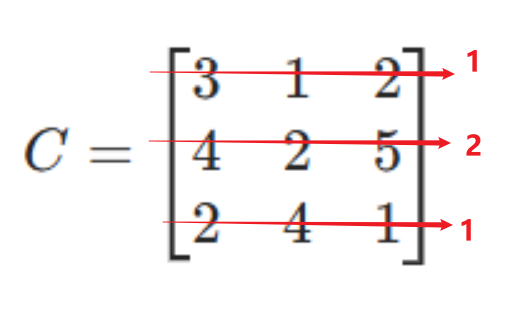
步骤1:行约减------每行减该行最小值
目的:让每行至少有1个0。
- 行1最小值=1 → 行1减1 → [2, 0, 1]
- 行2最小值=2 → 行2减2 → [2, 0, 3]
- 行3最小值=1 → 行3减1 → [1, 3, 0]
行约减后矩阵:
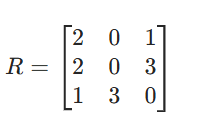
步骤2:列约减------每列减该列最小值
首先检查每一列是否有至少有一个0,如果有的话,跳过步骤2。
如果没有的话,执行步骤2,让每列至少有1个0。
- 列1最小值=1 → 列1减1 → [1, 1, 0]
- 列2最小值=0 → 不变
- 列3最小值=0 → 不变
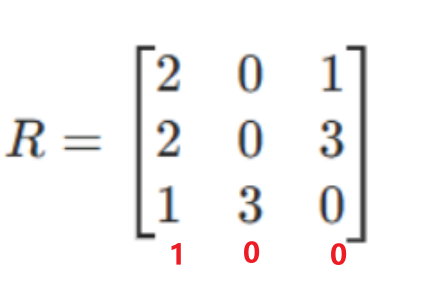
列约减后矩阵:
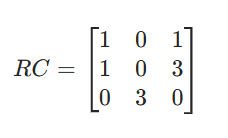
步骤3:用最少的直线覆盖所有0元素
核心:判断是否能找到 n 个独立的0,也就是覆盖线数量 k 需等于 n 。
用尽量少的线来覆盖0元素,检查:
- 若线的数量 k 小于n,构造新的0元素,执行步骤4
- 若等于n,步骤5
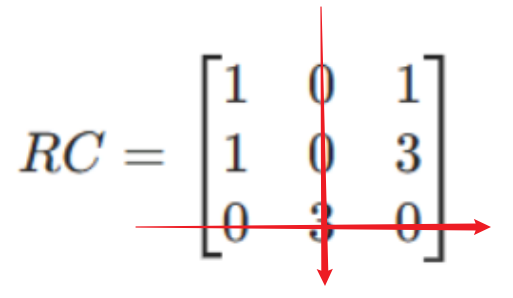
共2条线, k=2 < n=3 。
步骤4:构造新的0元素(当 k < n 时)
-
在所有未被覆盖的元素中,找到最小元素,记作k
-
然后把所有未被线覆盖的元素减去k
-
再把k加到线交叉的地方的元素上
-
然后再次执行步骤3
1 0 1
1 0 3
0 3 00 0 0
0 0 2
0 3 00 0 0
0 0 2
0 4 0
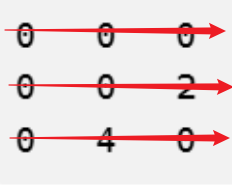
步骤 5:寻找独立的 0 元素(最优匹配)
结论:3 种最优方案
总成本最小都是 6,对应的分配方案为:
人员 1→任务 2,人员 2→任务 1,人员 3→任务 3
人员 1→任务 3,人员 2→任务 2,人员 3→任务 1
人员 1→任务 1,人员 2→任务 2,人员 3→任务 3
匈牙利算法总结
- 用尽量少的线来覆盖0元素
- 判断是否停止循环
- 假如使用n条线就能覆盖当前的所有0元素,那就停止循环
- 如果用的线少于n条线,继续循环(n是图中节点u或者节点v的数量)
- 在矩阵中产生更多的0元素
- 在所有没有被覆盖的元素中,找到最小元素,记作k
- 然后把所有没有被线覆盖的元素减去k
- 在把k加到线交叉的地方去
- 然后就完成了本轮循环,开始下一轮循环
三、求解
设人员为行,任务为列,成本矩阵 ( C ) 为:
C = [ 9 2 7 8 6 4 3 7 5 8 1 8 7 6 9 4 ] C = \begin{bmatrix} 9 & 2 & 7 & 8 \\ % 人员1 6 & 4 & 3 & 7 \\ % 人员2 5 & 8 & 1 & 8 \\ % 人员3 7 & 6 & 9 & 4 \\ % 人员4 \end{bmatrix} C= 9657248673198784
步骤1:行约减(每行减去该行最小值)
目标:让每行至少出现1个0元素。
- 行1最小值: min ( 9 , 2 , 7 , 8 ) = 2 \min(9,2,7,8)=2 min(9,2,7,8)=2→ 行1减2:( [9-2, 2-2, 7-2, 8-2] = [7, 0, 5, 6] )
- 行2最小值: min ( 6 , 4 , 3 , 7 ) = 3 \min(6,4,3,7)=3 min(6,4,3,7)=3→ 行2减3:( [6-3, 4-3, 3-3, 7-3] = [3, 1, 0, 4] )
- 行3最小值: min ( 5 , 8 , 1 , 8 ) = 1 \min(5,8,1,8)=1 min(5,8,1,8)=1 → 行3减1:( [5-1, 8-1, 1-1, 8-1] = [4, 7, 0, 7] )
- 行4最小值: min ( 7 , 6 , 9 , 4 ) = 4 \min(7,6,9,4)=4 min(7,6,9,4)=4 → 行4减4:( [7-4, 6-4, 9-4, 4-4] = [3, 2, 5, 0] )
行约减后矩阵 ( R ):
R = [ 7 0 5 6 3 1 0 4 4 7 0 7 3 2 5 0 ] R = \begin{bmatrix} 7 & 0 & 5 & 6 \\ 3 & 1 & 0 & 4 \\ 4 & 7 & 0 & 7 \\ 3 & 2 & 5 & 0 \\ \end{bmatrix} R= 7343017250056470
步骤2:列约减(每列减去该列最小值)
目标 :让每列至少出现1个0元素(若已有则无需操作)。
计算每列的最小值:
- 列1: min ( 7 , 3 , 4 , 3 ) = 3 \min(7,3,4,3)=3 min(7,3,4,3)=3 → 列1减3:( [7-3, 3-3, 4-3, 3-3] = [4, 0, 1, 0] )
- 列2: min ( 0 , 1 , 7 , 2 ) = 0 \min(0,1,7,2)=0 min(0,1,7,2)=0 → 无需操作
- 列3: min ( 5 , 0 , 0 , 5 ) = 0 \min(5,0,0,5)=0 min(5,0,0,5)=0 → 无需操作
- 列4: min ( 6 , 4 , 7 , 0 ) = 0 \min(6,4,7,0)=0 min(6,4,7,0)=0 → 无需操作
列约减后矩阵 ( RC ):
R C = [ 4 0 5 6 0 1 0 4 1 7 0 7 0 2 5 0 ] RC = \begin{bmatrix} 4 & 0 & 5 & 6 \\ 0 & 1 & 0 & 4 \\ 1 & 7 & 0 & 7 \\ 0 & 2 & 5 & 0 \\ \end{bmatrix} RC= 4010017250056470
步骤3:寻找覆盖所有0元素的最少直线
目标:判断覆盖线数量是否等于 ( n=4 )(若等于,则可找到独立0元素)。
首先标记所有0元素的位置:
- 行1:( (1,2) )
- 行2:( (2,1), (2,3) )
- 行3:( (3,3) )
- 行4:( (4,1), (4,4) )
尝试用最少直线覆盖:
- 选列2(覆盖 ( (1,2) ));
- 选列3(覆盖 ( (2,3), (3,3) ));
- 选列1(覆盖 ( (2,1), (4,1) ));
- 选列4(覆盖 ( (4,4) ));
共4条直线(等于 ( n=4 )),说明可以找到 ( n ) 个独立的0元素。
步骤4:匹配独立的0元素(最优分配)
规则:每个行、列仅选1个0元素,对应原矩阵的成本即为分配方案。
逐一匹配:
- 行1选择(1,2)。
- 行2选择(2,1)。
- 行3选择(3,3)。
- 行4选择(4,4)。
对应的原矩阵成本和:2+6+1+4=13,是最小总成本。
总成本最小的分配方案为:
- 人员1 → 任务2
- 人员2 → 任务1
- 人员3 → 任务3
- 人员4 → 任务4
四、代码
cpp
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
// 匈牙利算法
// cost: 成本矩阵 ,n x n
// 返回: 最小总成本
int hungarian(const vector<vector<int>>& cost, int n) {
vector<int> u(n+1), v(n+1), p(n+1), way(n+1);
for (int i = 1; i <= n; ++i) {
p[0] = i;
int j0 = 0;
vector<int> minv(n+1, INT_MAX);
vector<bool> used(n+1, false);
do {
used[j0] = true;
int i0 = p[j0], delta = INT_MAX, j1;
for (int j = 1; j <= n; ++j) {
if (!used[j]) {
int cur = cost[i0-1][j-1] - u[i0] - v[j];
if (cur < minv[j]) {
minv[j] = cur;
way[j] = j0;
}
if (minv[j] < delta) {
delta = minv[j];
j1 = j;
}
}
}
for (int j = 0; j <= n; ++j) {
if (used[j]) {
u[p[j]] += delta;
v[j] -= delta;
} else {
minv[j] -= delta;
}
}
j0 = j1;
} while (p[j0] != 0);
do {
int j1 = way[j0];
p[j0] = p[j1];
j0 = j1;
} while (j0 != 0);
}
int total_cost = 0;
for (int j = 1; j <= n; ++j) {
total_cost += cost[p[j]-1][j-1];
}
return total_cost;
}
// 回溯法找出所有最优方案
void backtrack(const vector<vector<int>>& cost, int n, int person,
vector<int>& taskAssigned, vector<bool>& usedTask,
int currentCost, int minCost, vector<vector<int>>& allSolutions) {
if (person == n) {
if (currentCost == minCost) {
allSolutions.push_back(taskAssigned);
}
return;
}
for (int task = 0; task < n; ++task) {
if (!usedTask[task]) {
usedTask[task] = true;
taskAssigned[person] = task;
backtrack(cost, n, person + 1, taskAssigned, usedTask,
currentCost + cost[person][task], minCost, allSolutions);
usedTask[task] = false;
}
}
}
int main() {
int n;
cout << "请输入矩阵大小 n:";
cin >> n;
vector<vector<int>> cost(n, vector<int>(n));
cout << "请输入 " << n << "x" << n << " 成本矩阵:" << endl;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
cin >> cost[i][j];
}
}
// 第一步:用匈牙利算法求最小总成本
int minCost = hungarian(cost, n);
// 第二步:回溯找出所有最优方案
vector<int> taskAssigned(n, -1);
vector<bool> usedTask(n, false);
vector<vector<int>> allSolutions;
backtrack(cost, n, 0, taskAssigned, usedTask, 0, minCost, allSolutions);
// 输出所有最优方案
cout << "\n所有最优方案:" << endl;
for (int k = 0; k < allSolutions.size(); ++k) {
cout << "方案 " << k + 1 << ":" << endl;
int total = 0;
for (int i = 0; i < n; ++i) {
int t = allSolutions[k][i];
cout << "人员" << (i + 1) << ":任务" << (t + 1)
<< ",成本:" << cost[i][t] << endl;
total += cost[i][t];
}
cout << "该方案总成本:" << total << "\n" << endl;
}
cout << "最小总成本为:" << minCost << endl;
return 0;
}运行结果:
